基于灰色GM(1,1)殘差修正模型的動車組故障率預測*

杜文然，陸 航，楊濤存，徐貴紅

（1 中國鐵道科學研究院 研究生部，北京100081；2 中國鐵道科學研究院集團有限公司 機車車輛研究所，北京100081；3 中國鐵道科學研究院集團有限公司 電子計算技術研究所，北京100081）

隨著我國高速鐵路的迅速發展，動車組保有量逐年增多。動車組安全運營是保障鐵路安全運營的必要條件之一。對動車組一定周期內的百萬公里故障率進行預測，對于宏觀掌握動車組運行狀態，分析動車組運行安全規律，了解動車組安全裕度具有重要意義。

我國動車組具有大范圍跨線開行、運行環境復雜多變等特點。動車組故障的形成是多種復雜因素共同作用的結果，除了設備自身的狀態惡化外，還受人為因素、自然因素等多種復雜因素的影響，這些因素有多種多樣的表征形式，并且很可能耦合交叉共同作用。在影響動車組百萬公里故障率的各種因素中，諸多因素的不確定性較強，難以量化分析。灰色系統理論是處理不確定性半復雜問題的有效方法，在一些影響因素難以定量分析的領域得到了廣泛應用［1］。灰色系統理論已成功地應用于醫學、圖像處理、機器人、工業技術等方面并取得實效［2］。在水上交通運輸領域，灰色系統理論被用來預測船舶交通事故，揭示船舶交通事故與其相關影響因素之間的規律性，對船舶交通事故短期預測有較好的效果［3］。在軌道交通領域，采用灰色系統理論預測鐵路客、貨運量未來發展趨勢［4-6］，應用灰色GM（1，1）非等時距修正模型模擬軌道質量指數的趨勢成分與波動成分［7］。對于動車組運行故障趨勢的預測目前未見相關文獻。文中利用灰色理論，以某分析類別動車組百萬公里故障數據為原始時間序列，深入挖掘動車組故障數據的特點，研究建立了用于動車組百萬公里故障率預測的灰色GM（1，1）殘差修正模型。

1 動車組百萬公里故障率數據特點

隨著中國鐵路運營里程的增加，投入運行的動車組也不斷增多。為了更加清晰地分析相同的速度級或者相同修程條件下動車組的安全規律，考慮我國動車組既有的修程設置（主要是相同檢修周期的不同走行公里的規定）和速度等級（主要考慮200～250 km/h、300～350 km/h 這2 個速度級），將不同車型動車組劃分為4 個分析類別，具體劃分方法見表1。

文中以某分析類別動車組百萬公里故障率數據為例，研究建立灰色GM（1，1）殘差修正模型。該分析類別動車組百萬公里故障率數據變化趨勢如圖1 所示。

圖1 呈現出該分析類別動車組百萬公里故障率數據具有如下特點：

（1）非線性；

（2）數據波動變化具有動態隨機性。

灰色預測模型是預測理論中的一種重要方法，是一種研究少數據、貧信息不確定性問題的方法［8］。它的突出優點是可以有效地處理系統內部信息的不確定性因果關系，通過對時間序列的累加，弱化其隨機性［9］。文中采用灰色系統理論，建立灰色GM（1，1）殘差修正模型，對動車組百萬公里故障率進行研究。

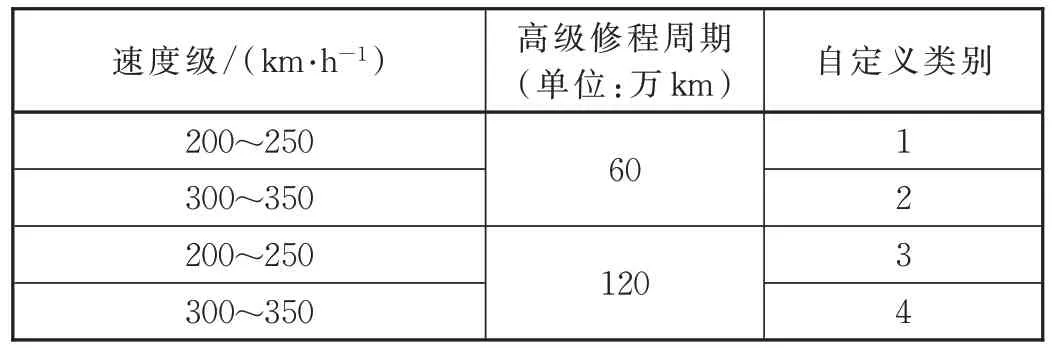
表1 動車組自定義分析類別劃分說明

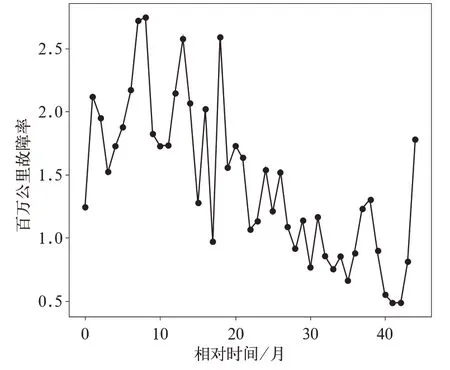
圖1 某分析類別動車組百萬公里故障率變化趨勢圖

2 GM(1,1)模型的建立[7-10]

由文獻［7］可知，灰色GM（1，1）模型可分為等時距模型和非等時距模型。文中建立的模型為等時距模型，時間間隔為1 個月。

（1）設某分析類別動車組的百萬公里故障率數據序列為X(0)={ x(0)(1)，x(0)(2)，…，x(0)(n)}，對原始序列構造一次累加生成（1-AGO）序列，得：X(1)={ x(1)(1)，x(1)(2)，…，x(1)(n)}，令 x(1)(1)=x(0)(1)；式中：

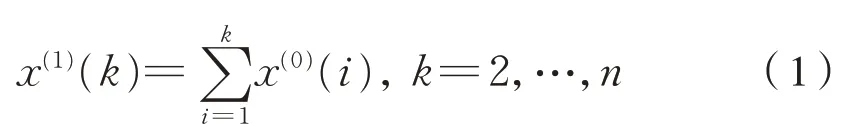
（2）由生成序列X（1）建立白化形式的微分方程為式（2）。

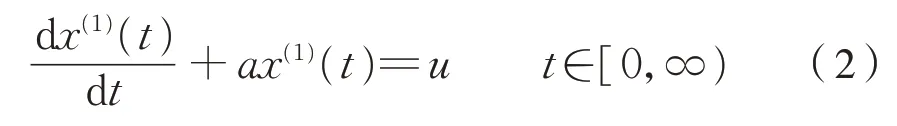
式中：a 為發展系數，用以控制灰色系統發展態勢的大小；u 用以反映數據變化的不確切關系，又稱為灰色作用量［7］。

對式（2）在區間[k-1，k]上積分，得到式（3）：

GM（1，1）模型的擬合精度與參數a^ =[a，u]T有關，而a^ =[a，u]T的取值又依賴于原始序列和背景 值 Z(1)=(z(1)(2)，z(1)(3)，…，z(1)(n)) 的 構 造 形式［7］，為了提高模型精度，減小誤差，文獻［7，10］提出了一種基于積分重構GM（1，1）模型背景值的方法，按照該方法，對Z(1)進行優化的計算方法為式（9）：

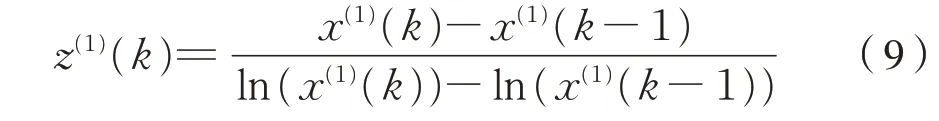
式中：k=2，…，n。文獻［7，10］證明按照式（9）構造的背景值更接近實際。

3 殘差修正

為進一步提高模型的擬合度，對殘差序列進行修正，修正方法如下：

設殘差數列為式（10）：

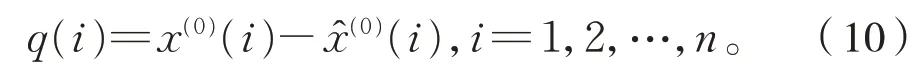
設 樣 本 集D={(x1，q1)，(x2，q2)，…，(xn，qn)}，回歸問題就是找到一個函數f(x)，使得f(xi)與真實值qi的誤差能夠盡可能小。以支持向量機SVM（Support Vector Machine）為理論基礎建立的回歸模型，在準確度、收斂速度和風險控制等方面都有很好的性能［11］。因此用支持向量回歸機SVR（Support Vector Regression）對殘差數列Q進行回歸擬合。

對 于 訓 練 集D={(x1，q1)，(x2，q2)，…，(xn，qn)}為非線性的情況，支持向量回歸機的基本思想是通過一個非線性函數Φ，將數據x映射到高維特征空間F，并在這個特征空間進行回歸［12］。

為了提高預測精度，在用支持向量回歸機對殘差進行回歸擬合時，把t-k，t-（k-1），…，t-1 時刻的殘差作為輸入，t時刻的殘差作為相應的輸出。經參數調整，把t-3，t-2，t-1 時刻的殘差作為輸入，t時刻的殘差作為輸出時，擬合的精度較高。核函數選擇高斯核函數時，對殘差的擬合精度較高。

對 殘 差 數 列Q={q(1)，q(2)，…，q(n)} 用 支 持向量回歸機進行回歸擬合，得到殘差的擬合數據序列，見式（11）：

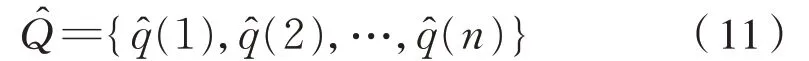
根據式（8）、式（10）和式（11），得到最終優化的灰色GM（1，1）修正模型為式（12）：

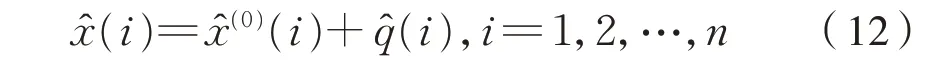
4 模型實例應用檢驗

采用某分析類別動車組在相對時間0～44 個月的百萬公里故障率數據。用文中給出的優化背景值后的灰色GM（1，1）模型對該分析類別動車組在該時間段內的百萬公里故障率數據進行擬合，原始百萬公里故障率數據及其擬合結果對比如圖2所示。

圖2 表明該分析類別動車組百萬公里故障率總體上呈現出下降的趨勢。由真實值減去優化背景值后的灰色GM（1，1）模型擬合值得到的殘差如圖3 所示。

圖3 顯示出該分析類別動車組百萬公里故障率數據的殘差呈現非線性的正負交替的情況，這說明原始百萬公里故障率數據中含有一定的隨機成分。動車組故障形成是多種因素共同作用的結果，且動車組行車環境復雜，得到的殘差具有隨機波動性，符合實際意義。圖3 呈現的殘差變化波動趨勢與圖1 原始百萬公里故障率數據的變化波動趨勢相似，進一步說明優化背景值后的灰色GM（1，1）模型能夠較好的呈現該分析類別的動車組在該時間段內的百萬公里故障率的趨勢成分。為了提高模型的擬合精度，用支持向量回歸機對殘差 進 行 修 正，將t-3，t-2，t-1 時 刻 的 殘 差 作 為輸入，t時刻的殘差作為輸出，核函數選用高斯核函數。經過超參數調整后，原始百萬公里故障率數據與經過殘差修正后的百萬公里故障率擬合數據的對比如圖4 所示。

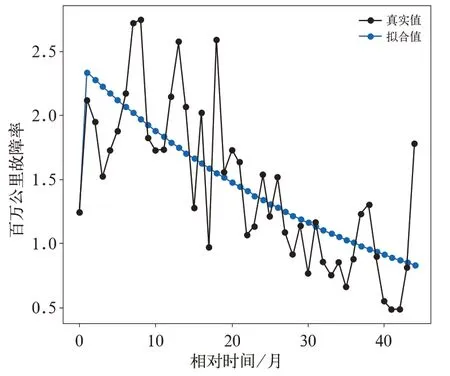
圖2 百萬公里故障率及其擬合結果對比

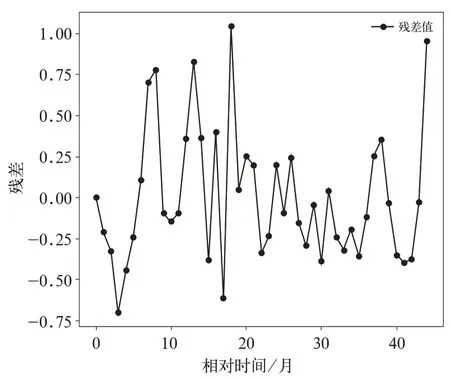
圖3 殘差變化趨勢圖

用平均相對誤差作為檢驗指標時，圖4 中的灰色GM（1，1）殘差修正模型得到的百萬公里故障率擬合值與真實值的平均相對誤差為0.076；用統計學中的后驗差C和小概率P檢驗法［7，9］進行模型精度檢驗，得到后驗差比值C=0.150，小誤差頻率P=1.00；由文獻［9，15］可知，一般根據C、P的值將預測精度分為4 級，見表2。

對照上表可以看出文中給出的灰色GM（1，1）殘差修正預測模型的精度屬于好的范疇，可以用于外推預測。

用圖4 得到的灰色GM（1，1）殘差修正模型對相對時間45 個月的百萬公里故障率數據進行預測，得到預測值為0.85，相對時間45 個月的百萬公里故障率數據的真實值為0.81，相對誤差為4.94%。

將相對時間45 個月的百萬公里故障率數據加入模型，刪除原始百萬公里故障率數據中的第一個數據，進行模型更新，得到新的等維灰色GM（1，1）殘差修正模型，用此模型對相對時間46 個月的百萬公里故障率進行預測。依次類推，得到相對時間47～49 個月的故障率預測模型。相對時間46～49 個月的原始百萬公里故障率數據與模型擬合值的對比如圖5 所示。

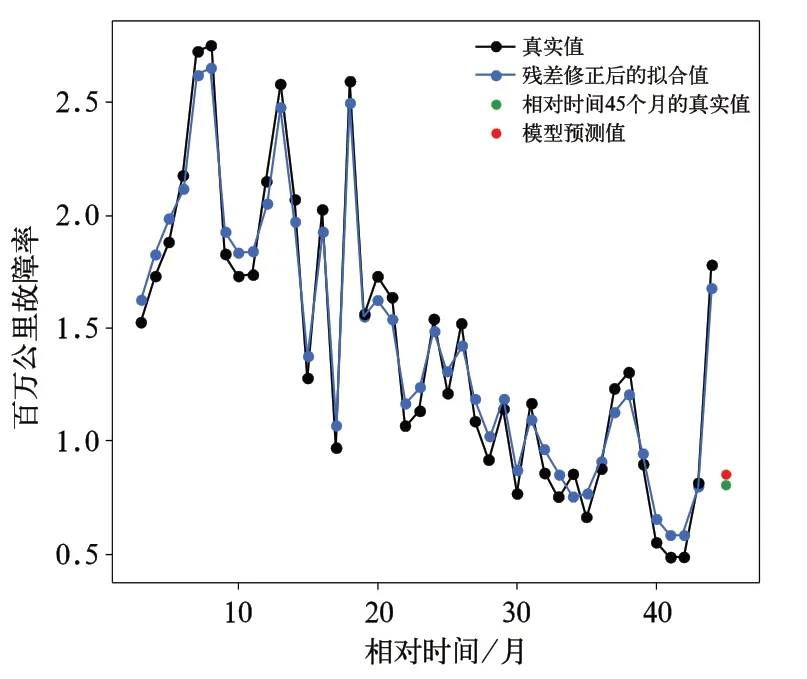
圖4 原始百萬公里故障率與殘差修正后的擬合結果對比

表2 精度檢驗等級參照表

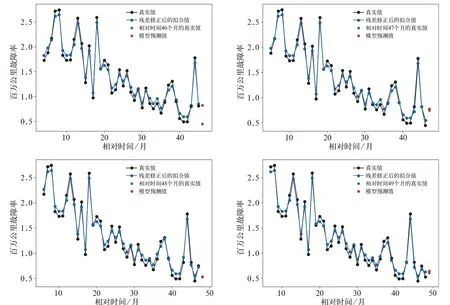
圖5 相對時間46～49 個月的原始百萬公里故障率與殘差修正后的擬合結果對比

相對時間46～49 個月的故障率預測模型的各項評價指標見表3。

由表3 可知，殘差修正后的等維灰色GM（1，1）模型能較好地擬合百萬公里故障率數據的變化趨勢以及波動大小。

用等維灰色GM（1，1）殘差修正模型對相對時間45～49 個月的百萬公里故障率的預測值與真實值的對比見表4。

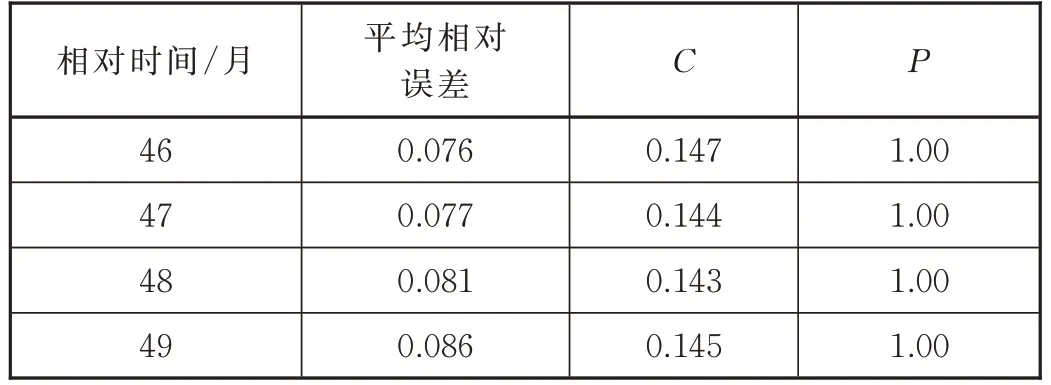
表3 各預測模型指標值

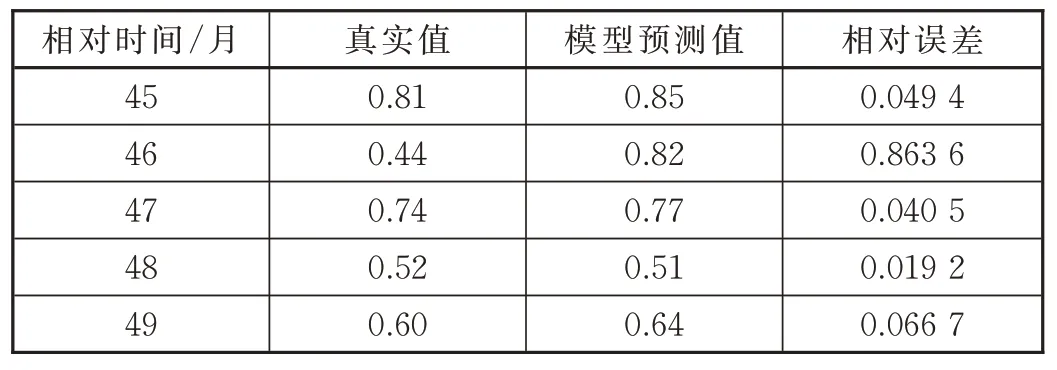
表4 模型預測值與真實值的比較

5 結 論

（1）根據灰色系統理論的時間序列處理原則，在等時距灰色GM（1，1）模型的基礎上，通過優化背景值的方法，建立了預測動車組百萬公里故障率變化趨勢的模型，利用支持向量回歸機對優化背景值后的灰色GM（1，1）模型的殘差進行修正，擬合了某分析類別動車組百萬公里故障率數據的波動大小，并通過等維信息灰色GM（1，1）模型來對建模數據進行更新。計算實例表明，等維灰色GM（1，1）殘差修正模型能夠較好的擬合動車組百萬公里故障率的變化趨勢與波動程度，且有較好的預測精度。

（2）由于用來建模的原始百萬公里故障數據波動較大，給長期預測帶來了挑戰。計算實例表明，該模型能夠較好地擬合歷史數據，卻無法預測出現較大波動的數據，如何進一步處理原始數據，減小原始數據波動性對模型性能的影響以及挖掘更多影響百萬公里故障率的因素是下一步研究的內容。