一種面向訂單剩余完工時間預測的SOM-FWFCM特征選擇算法

劉道元 郭 宇 黃少華 方偉光 楊能俊 崔世婷

南京航空航天大學機電學院，南京，210016

0 引言

日益激烈的市場競爭和復雜多變的客戶需求對制造企業縮短產品生產周期、按時交付訂單提出了更高的要求，訂單剩余完工時間的準確預測能夠為動態的生產計劃調整、生產過程優化提供合理的判別依據，對訂單產品的準時完工具有重要的指導意義[1]。在當前生產方式靈活、產品種類繁多的離散制造車間中，智能傳感器的大量應用為預測訂單剩余完工時間提供了海量的生產數據[2]，但同時也帶來了“維度災難”的問題，因此有必要設計一種合理的特征選擇方法來有效地從眾多特征中獲取關鍵特征，以降低求解問題的復雜度，提高預測模型與實際生產運行規律的擬合度，保證預測的準確性。

特征選擇是指從候選特征中挑選若干個具有代表性的特征組成關鍵特征子集，當前的主要研究方法包括封裝式和過濾式特征選擇算法。

封裝式特征選擇算法需要對每個特征子集進行學習器訓練，根據學習器性能選擇關鍵特征子集。相關學者使用量子遺傳算法[3]、改進粒子群算法和禁忌搜索相結合[4]、粗糙集相對分類信息熵和粒子群算法相結合[5]的方法進行特征選擇，首先對每個特征進行編碼，然后根據學習器的預測結果計算適應度值，不斷迭代至收斂，最后選擇適應度值最高的特征子集作為關鍵特征子集。ZHONG等[6]使用SVM-RFE算法構建特征空間，然后使用皮爾森系數剔除特征空間中有相同意義的特征，最終從26個候選特征中選擇6個特征組成最優特征子集。DY等[7]使用期望最大化算法選擇特征，以特征子集的分散可分性和最大似然為評價指標，經過多次修改算法參數，選擇評價最優的特征子集。上述封裝式特征選擇算法能得到高質量的特征子集，但每次迭代都需要訓練學習器，導致計算復雜度高，不適合處理大規模數據[8]。

過濾式特征選擇算法直接通過某種準則選擇關鍵特征子集，再訓練后續學習器，特征選擇過程與學習器無關，在處理大規模數據方面，降低了計算復雜度，運行效率較高。朱雪初等[9]使用運行效率高、對噪聲有一定容錯能力的ReliefF算法進行特征選擇，考慮各特征與預測目標的相關性但忽略了特征間的冗余性。基于最大相關性-最小冗余性原則，PENG等[10]和夏虎等[11]分別使用互信息和皮爾森系數計算參數間的相關性和冗余性，完成最佳特征子集的選擇。為了提高關鍵特征子集的質量和后續學習器的精度，特征選擇不僅要滿足最大相關性-最小冗余性原則，還需要最大化特征間的多樣性[12]。LIU等[13]通過互信息和關聯系數分別衡量類間和類內距離，將標簽數據作為單獨一類，采用類似于凝聚層次聚類的算法確定關鍵特征子集。ZHOU等[14]以屬性間的最大信息系數作為距離矩陣，使用K-mode算法對屬性進行聚類完成特征選擇。WITTEN等[15]提出稀疏聚類框架，使用稀疏K均值聚類和稀疏層次聚類算法相結合的方法完成特征選擇。

在上述基于聚類的特征選擇方法中，減少了特征間的冗余性，保證了特征間的多樣性，但每個特征對預測目標解釋能力不同，需要根據特征的解釋能力來指導特征聚類。本文在特征聚類過程中引入描述特征對預測目標解釋能力的特征權重，解釋能力越強的特征在計算聚類中心時貢獻越大，選擇其為關鍵特征的概率越高，通過綜合考慮關鍵特征子集的冗余性、多樣性以及與目標的相關性，實現關鍵特征的準確選擇。

本文提出了一種基于自組織映射(self-organizing map, SOM)網絡-特征權重模糊C均值(feature weighted fuzzy C-means, FWFCM)聚類的過濾式特征選擇算法，利用SOM網絡為FWFCM算法提供初始簇中心，以避免FWFCM算法對初始聚類中心敏感、容易陷入局部最優的問題；將基于互信息的特征與目標相似度作為特征權重，使特征聚類過程具有一定的導向性，進一步改善聚類效果和提高關鍵特征子集質量。最后結合某航天機加工車間提供的19 428條具有1102個特征的生產數據，進行算法的實例驗證和對比分析，證明了所提方法的有效性。

1 問題描述

訂單剩余完工時間(order remaining completion time, ORCT)是指從當前時刻開始到訂單所有零件產出的時間長度，即TORC=Tfin-Tcur，其中，Tfin表示訂單所有零件產出時刻，Tcur表示當前時刻。在復雜離散制造系統中，影響訂單完工時間的不確定因素很多，為便于討論，本文考慮的制造過程遵循以下原則：①離散制造車間中有M個工位，用于生產P類不同零件，每個工位都包含一臺機床、一個入緩存區和一個出緩存區；②每個零件有唯一確定的加工路線；③每個在制品在同一臺機床上只加工一次；④選擇入/出緩存區在制品運輸/加工遵循先入先出的原則；⑤在制品準備加工時間包含在在制品加工時間內，在制品在固定兩個工位之間的運輸時間設為常數。

基于上述原則，訂單剩余完工時間主要取決于在制品在入/出緩存區的等待時間和在制品在所有工位上的加工時間。緩存區在制品種類、數量和優先級對訂單完成加工時間有著重要的影響[16]。在制品在某個工位的生產過程可以分為以下3個步驟：①在制品從上個工位運輸到此工位，進入入緩存區等待加工；②在機床上完成加工；③進入出緩存區等待運輸到下一個工位。

根據上述車間特點，將車間生產任務、實時生產狀態以及生產統計數據三類信息作為候選特征。定義所有候選特征組成的集合為候選特征集。車間生產任務包含一個/多個訂單中各類零件數量；實時生產狀態包括入/出緩存區在制品隊列、每臺機床正在加工的在制品種類以及正在運輸的在制品信息四類在制品狀態信息，還包括設備狀態(“加工中”“等待中”“故障中”“維修中”)和設備負載兩類設備運行狀態信息；生產統計數據包括機床正在加工的在制品加工時長、機床利用率及其持續加工時長、訂單中各類未開工零件數。

車間各生產要素相互影響，部分數據特征相互依賴，候選特征集具有一定的冗余性。冗余特征會造成計算復雜度急劇上升、預測模型訓練困難及精度下降等問題，所以提出一種基于SOM-FWFCM的特征選擇算法來實現關鍵特征選擇，減少計算復雜度，提高預測精度。

2 特征選擇算法

圖1 基于SOM-FWFCM算法的特征選擇流程圖Fig.1 Flow chart of feature selection based onSOM-FWFCM algorithm

SOM-FWFCM是一種在聚類過程中考慮特征與預測目標之間相關性的過濾式特征選擇算法，擺脫了FWFCM算法需設置初始聚類中心的困擾，避免了聚類過程的盲目性，實現了高質量的關鍵特征選擇，算法的總體流程如圖1所示。首先通過互信息[17]量化特征與目標之間的關聯關系程度來定義任意特征對預測目標的重要因子，即特征權重；其次將候選特征集輸入SOM網絡，確定FWFCM的初始聚類中心和簇數；然后不斷迭代更新FWFCM的聚類中心和特征隸屬度，實現導向性特征聚類；最后剔除冗余特征，得到訂單剩余完工時間預測的關鍵特征子集。

2.1 特征權重

互信息是一個隨機變量包含另一個變量的信息量的度量，能夠表達任意特征與輸出向量之間的相關程度[18]。兩個隨機變量x和變量y的互信息定義如下：

(1)

其中，l表示隨機變量x或變量y的維數，x={x1,x2,…,xl}，y={y1,y2,…,yl}，I(x,y)表示變量x和變量y的互信息，p(xi,yj)表示x=xi且y=yj的概率，p(xi)表示x=xi的概率，p(yj)表示y=yj的概率。當變量x和變量y相互獨立時，p(xi,yj)=p(xi)p(yj)，互信息I(x,y)=0；變量x包含變量y信息量越多，互信息I(x,y)的值越大。

任意特征對預測目標的解釋能力可以用互信息衡量，換言之，互信息可以量化任意特征對預測目標的重要程度。定義描述特征重要程度的特征權重為

(2)

其中，wi表示第i個特征的權重，I(fxi,fy)表示第j個特征fxi與預測目標fy的互信息，n表示候選數據特征集的特征數。I(fxi,fy)的值越大，對目標的解釋能力越強，特征越重要，特征權重越大。

2.2 SOM-FWFCM算法

SOM網絡能夠自動對輸入數據進行聚類，并且容易實現，但精確度不高；而模糊C均值(FCM)算法具有良好的聚類準確度，但聚類前必須確定初始聚類中心或初始隸屬度。本文將SOM網絡和FCM算法相結合，保證FCM算法初始聚類中心的可靠性，提高聚類結果的準確度。

SOM網絡將高維特征集映射到低維空間(一般為二維)，并擁有在高維空間的拓撲結構[19]。將某個特征輸入SOM網絡中，計算輸出層獲勝神經元，即該特征在低維空間中的位置，映射在同一位置的輸入特征劃分為同一簇。在訓練網絡過程中，首先確定輸出層拓撲結構(a×a)，初始化權向量W，設定初始學習率及迭代次數；然后計算輸入特征對應的獲勝神經元，根據獲勝神經元確定周邊興奮神經元的空間位置，即優勢領域；最后更新興奮神經元攜帶的權向量，縮小權向量與輸入特征集之間的距離，不斷迭代直至最大迭代次數。權向量更新規則如下：

Wi,j=Wi,j+η(t)|pxi-Wi,j|

(3)

(4)

(5)

其中，Wi,j表示第i個輸入神經元節點與第j個輸出神經元之間的連接權重，η(t)表示第t次循環的學習率，pxi表示第i個輸入神經元的輸入，η0表示初始學習率，r(t)表示t次循環的優勢領域半徑，T表示最大迭代次數。

FCM算法[20]通過隸屬度確定每個對象屬于某個聚類的程度，最大化同一簇對象的相似度，同時最小化不同簇之間對象的相似度。與隸屬度只能為0或1的硬聚類算法相比，FCM算法更加符合現實要求，有著更好的聚類精度。FCM算法在訓練迭代過程中，僅根據特征空間分布情況進行標記，完全獨立于預測目標，這導致聚類缺乏一定的導向性。特征權重搭建特征與預測目標關聯的橋梁，特征權重值越大，該特征對預測目標的影響越大，被選擇為特征代表的可能性越大，在聚類過程中將其加以考慮，提高關鍵特征選擇的有效性和預測準確度。本文稱引入特征權重的FCM算法為FWFCM算法。定義FWFCM算法的數學模型如下：

(6)

(7)

其中，J表示FWFCM算法的目標函數；kc表示聚類中心數；wj表示第j個特征權重；μi,j表示第j個特征屬于第i個聚類中心的隸屬度；m表示模糊權重，取值范圍為[1,∞]，通常取m=2[21]，ci表示第i個聚類中心。

將上述有條件極值問題轉化為無條件極值問題，構造拉格朗日函數，引入拉格朗日因子，使得目標函數取得極小值，即

(8)

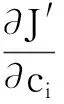
(9)

(10)

(11)

i=1,2,…,kcj=1,2,…,q

其中，λ表示拉格朗日因子，λ={λ1,λ2,…,λn}，Δf表示第t次相對于上次的隸屬度改變量最大值。FWFCM算法迭代過程如下：①使用式(10)～式(11)計算每個特征的權重；②根據SOM網絡得到初步的聚類結果及FWFCM的初始聚類中心，并初始化隸屬度矩陣；③計算每個特征的隸屬度，若Δf小于預設閾值，則算法結束，否則轉入步驟④；④更新kc個聚類中心，轉入步驟③。

FWFCM算法迭代結束后，根據隸屬度矩陣對各特征進行類別劃分，選取離簇中心最近的特征為該類的特征代表，構成關鍵特征子集。

3 案例分析

本文以某航天機加車間的19 648條生產數據為例進行實例驗證，將候選特征集輸入SOM-FWFCM、FWFCM、SOM-FCM、層次聚類[13](hierarchical clustering, HC)和權重K均值(weighted K-means，WK-means)聚類五種特征選擇算法中，得到關鍵特征子集，以關鍵特征子集為輸入訓練人工神經網絡(artificial neural network, ANN)完成剩余完工時間預測，對比分析聚類性能和預測結果準確度，驗證本文所提方法的有效性。

通過反復試驗，選擇特征選擇算法性能較好的參數如下：SOM網絡結構為15×15，迭代次數為100，初始學習率為0.5，FWFCM算法閾值為0.001。在聚類過程中，候選特征集屬于無類別標簽數據，選用Calinski-Harabaz(CH)系數和輪廓系數(silhouette coefficient, SC)度量聚類性能，計算公式如下：

(12)

(13)

(14)

(15)

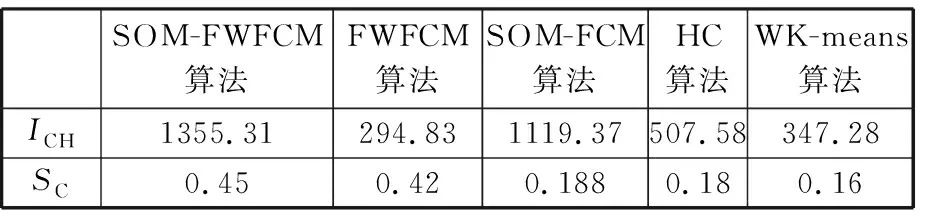
表1 不同算法的聚類結果分析

根據SOM-FWFCM算法從1102個候選特征中選擇69個特征構成關鍵特征子集，見表2，將其輸入ANN中，對比預測值與實際值的差值。若差值越小，表示預測越準確，所選特征越有效，特征選擇算法越具有優越性。

表2 訂單剩余完工時間預測關鍵特征子集

本文使用常用的均方根誤差(root mean square error, RMSE)、平均絕對誤差(mean absolute error, MAE)、平均絕對百分比誤差(mean absolute percentage error, MAPE)來評價預測準確性，計算公式如下：

(16)

(17)

(18)

在ANN訓練過程中，以RMSE值與L2正則項之和為損失函數，并加入Dropout層[22]，改善網絡的過擬合現象。如圖2所示，紅色線表示訓練集優化過程，藍色線表示測試集的測試過程。在網絡優化過程中，模型以較快的收斂速度收斂至較小值，并且具有較強的泛化能力，即訓練集預測誤差和測試集預測誤差接近。圖3描述的是從測試集中隨機挑選200個樣本作為預測對象，紅色線表示樣本真實值，藍色線表示對應樣本的預測值。由圖3可以看出，預測值與實際值的變化方向和幅度非常接近，并且預測值與實際值幾乎重合。由于車間存在不確定的擾動，導致圖3中極小部分預測值偏離實際值，造成預測不準確的假象，但總體而言，本文方法得到的剩余完工時間

圖2 SOM-FWFCM-ANN的優化過程Fig.2 Optimization process of SOM-FWFCM-ANN

圖3 SOM-FWFCM-ANN的預測結果Fig.3 Prediction results of SOM-FWFCM-ANN

預測值具有較高的準確度，能夠滿足現實車間生產要求。

為驗證本文所提出的特征選擇方法的有效性，進行以下實驗：使用上述5種特征選擇算法篩選得到相應的具有69、62、91、102、100個特征的關鍵特征子集，對不同的關鍵特征子集搭建ANN，預測訂單剩余完工時間，5種算法分別簡稱為SOM-FWFCM-ANN、FWFCM-ANN、SOM-FCM-ANN、HC-ANN 、WK-means-ANN。如圖4所示，分別以藍色線、綠色線、紅色線、青色線、黃色線表示這5種算法在測試集上的測試過程，HC-ANN、WK-means-ANN雖然以較快的速度收斂，但由于關鍵特征子集質量較差，導致推理能力欠缺，易陷入局部最優解；相對而言前三者預測精度較高，尤其在聚類過程中引入特征權重，考慮特征與目標之間的相關性，使特征選擇過程具有一定的導向性，提高了關鍵特征子集質量以及預測精度。表3通過RMSE、MAE、MAPE三個評價指標直觀地描述了5種模型與實際問題的擬合程度，可以看出SOM-FWFCM-ANN模型擬合程度最高、最準確，準確度從高到低依次是SOM-FWFCM-ANN、FWFCM-ANN、SOM-FCM-ANN、HC-ANN、WK-means-ANN。

圖4 不同模型的優化過程Fig.4 Optimization process of different models

表3 不同模型的結果對比

從本實驗可以得到以下結論：①SOM網絡為FWFCM算法提供的初始聚類中心優于隨機初始化聚類中心，提高了后者尋找最優解的能力；②在聚類過程中考慮特征權重，增加了重要特征在迭代計算過程的影響力，提高了聚類質量和特征選擇的有效性；③基于SOM-FWFCM的特征選擇模型能夠選擇反映車間運行規律的關鍵特征子集，減少了后續預測分析的運算復雜度，為訂單剩余完工時間的精準預測提供了基礎，證明了本文算法在復雜離散制造車間應用的可行性。

4 結語

本文通過分析每個候選特征的重要程度和關鍵特征子集的冗余性和多樣性，提出了一種適用于大規模數據集的特征選擇算法，即SOM-FWFCM算法。通過分析5種特征選擇算法聚類結果的類內凝聚度和類間分散度、訂單剩余完工時間預測值的準確度，驗證了本文所提算法的有效性。在后續研究中可以使用本文所選擇的關鍵特征進一步研究預測模型，提高預測的準確度，以及預測時發現車間生產任務不能按時完成，應采取何種調整策略來保證訂單按時交付。