一種高增益直流變換器的運行原理及數學建模

周雷

(國網寧夏電力有限公司電力科學研究院，寧夏 銀川 750011)

新能源作為一種清潔、高效、綠色、可持續的能源而備受國內外關注[1-3]，其在能源結構中的比重也逐年增大[4-6]。新能源發電主要包括光伏、風電及燃料電池發電等[7]，在光伏與燃料電池發電領域中，由于光伏電池和燃料電池的輸出電壓較低，為與高壓直流母線電壓等級相匹配[8]，需要使用升壓直流變換器對電源側的輸出電壓進行升壓。

經典Boost直流變換器因其結構簡單而被廣泛應用于各種場合，但其電壓增益由于開關器件自身特性而受到制約，無法實現較大的升壓比[9]。相比于經典Boost直流變換器，兩電平準Z源Boost直流變換器可實現很高的電壓增益，因此在大升壓比場景中該變換器被廣泛應用[10]。直流變換器的數學模型在穩態性能、誤差分析及控制策略研究等方面具有非常重要的作用[11],本文主要針對兩電平準Z源Boost直流變換器進行數學建模。

1 拓撲結構與運行原理

兩電平準Z源Boost直流變換器拓撲結構及運行狀態如圖1所示。圖1(a)為該變換器的拓撲結構，該變換器的拓撲由2個電感，1個功率開關，2個二極管及3個電容組成。圖中Uin為輸入電壓，iLl為電感L1電流，即輸入電流；流過電感L2的電流為iL2；功率開關Q的電壓應力(指功率開關Q關斷時承受的電壓)為UQ；二極管D1和D2的電壓應力(指二極管關斷時承受的電壓)分別為UD1和UD2；UC1，UC2和UC3為電容C1，C2和C3兩端的電壓；Uo為輸出電壓，Io為負載電流。電感L2，電容C1和C2以及二極管D1組成準Z源結構，電感L1，功率開關Q，二極管D2和電容C3組成Boost直流變換器的拓撲結構，二者組合可得兩電平準Z源Boost直流變換器的拓撲結構。設功率開關Q觸發脈沖占空比為d，該變換器運行原理分析如下：

運行狀態1。功率開關Q開通時(t0-t1)，二極管D1和D2關斷，此時拓撲的運行狀態如圖1(b)所示。電感L1和L2處于充電狀態，電容C1、C2和C3處于放電狀態：電源Uin和電容C1對電感L1充電，電感電流iLl線性上升；電容C2對電感L2充電，電感電流iL2線性上升。負載能量由電容C3提供。設開關周期為Ts，則有t1-t0=dTs。

運行狀態2。功率開關Q關斷時(t1-t2)，二極管D1和D2開通，此時拓撲運行狀態如圖1(c)所示。電感L1和L2處于放電狀態，電容C1、C2和C3處于充電狀態，電源Uin和電感L1對電容C2充電，電感L2對電容C1充電，電源Uin、電感L1和L2對電容C3充電,負載能量由電源Uin、電感L1和L2提供，此時有t2-t1=(1-d)Ts。

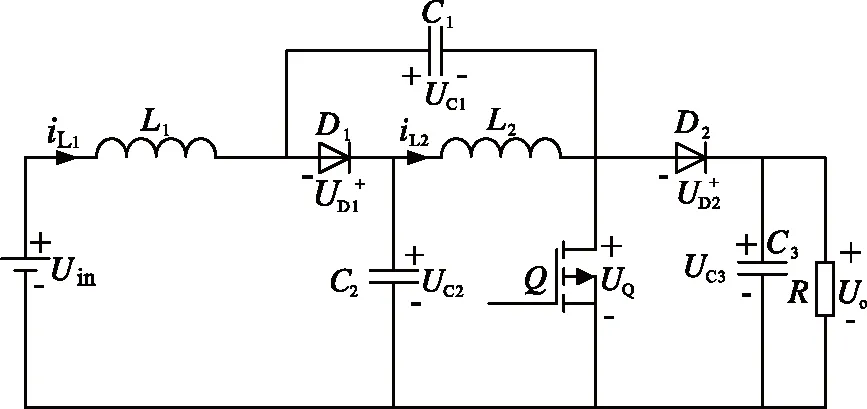
(a) 兩電平準Z源Boost直流變換器拓撲結構

該變換器主要工作波形見圖2。

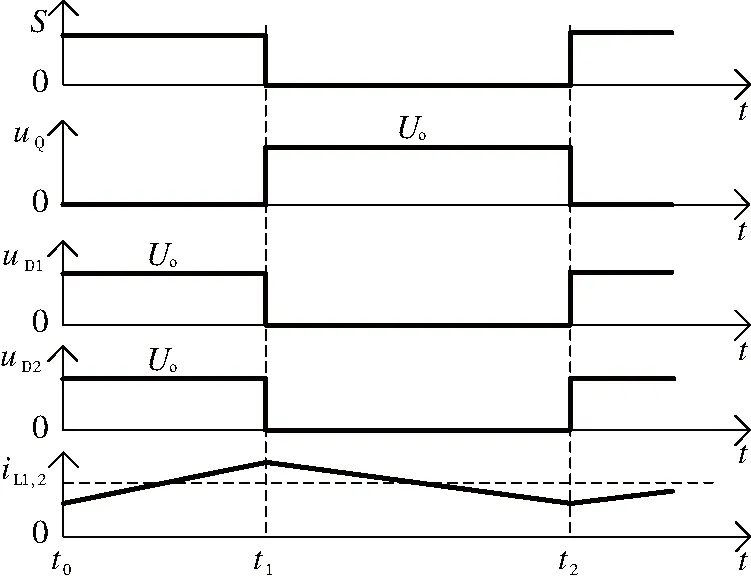
圖2 直流變換器主要工作波形

2 變換器的數學模型及穩態分析

狀態空間平均法是一種常用的直流變換器建模方法，該方法把儲能元件作為狀態變量，分別在不同開關狀態下建立相應狀態方程，通過將各狀態方程以時間加權的形式進行疊加，進而得到直流變換器的數學模型。狀態空間平均法要求不同開關狀態下的狀態方程階數必須相同，并且每個狀態變量都是獨立的。

對于兩電平準Z源升壓直流變換器，當功率開關Q開通時(見圖1(b))，儲能元件不存在耦合關系，電感電流iL1(t)、iL2(t)，電容電壓uC1(t)、uC2(t)和uC3(t)皆為獨立的狀態變量，可建立5階狀態方程；當功率開關Q關斷時(見圖1(c))，二極管D1和D2導通使電容C1，C2和C3構成僅容回路，電容電壓uC3(t)=uC2(t)+uC1(t)，三者相互耦合，存在一個無效狀態變量，只能建立4階狀態方程。由于不同開關狀態下狀態方程階數不同，無法使用狀態空間平均法建模。

考慮在電容C3支路串入寄生電阻r對電容電壓進行解耦，如圖3所示。當功率開關Q關斷時，電容C1，C2和C3不再構成電容回路，uC1(t)、uC2(t)、uC3(t)皆為獨立狀態變量，電容電壓實現解耦，此時可采用狀態空間平均法建立兩電平準Z源Boost直流變換器的平均狀態模型和小信號狀態模型。

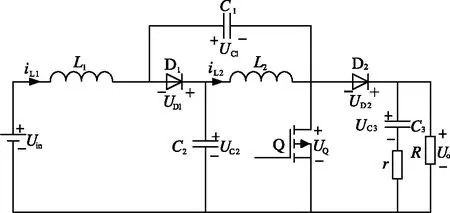
圖3 引入串聯電阻r的變換器拓撲結構

功率開關Q開通時，變換器運行狀態如圖1(b)所示，其狀態方程如式(1)所示；功率開關Q關斷時，變換器運行狀態如圖1(c)所示，其狀態方程如式(2)所示。

根據狀態空間平均法，由式(1)和式(2)可得變換器的平均狀態模型,如式(3)所示。

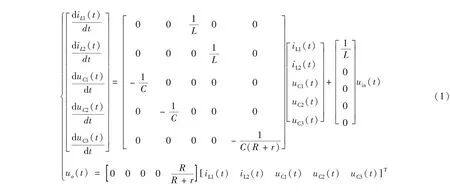
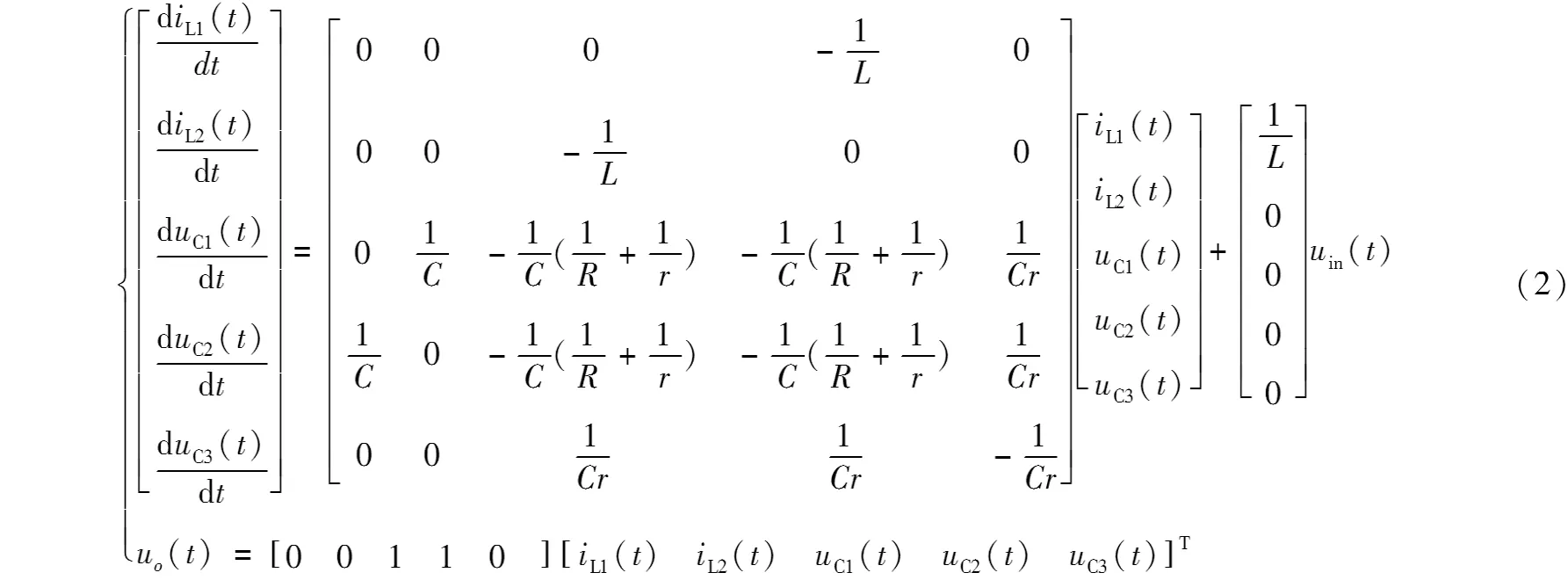
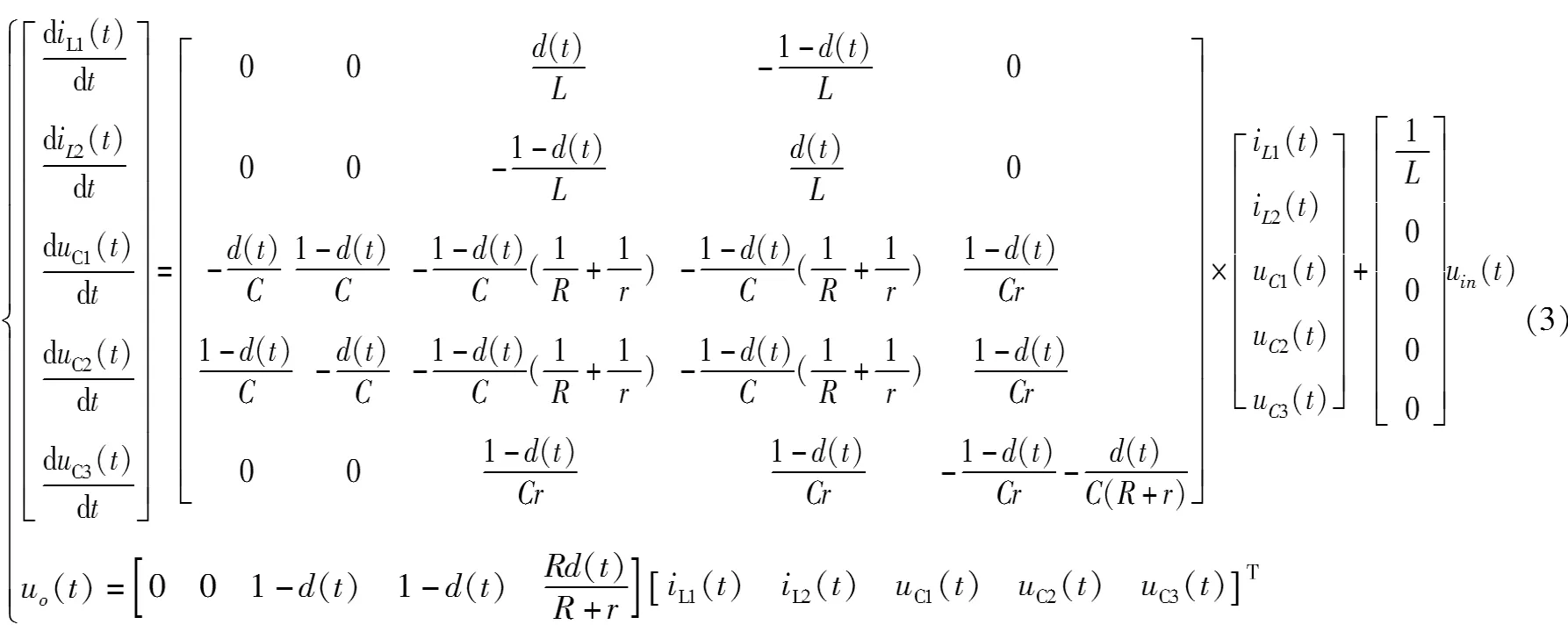
根據圖1(c)，功率開關Q關斷時，二極管D1和D2開通，此時有電容電壓UC3=UC1+UC2，根據伏秒平衡原則，對電感L1與L2列出如下方程：

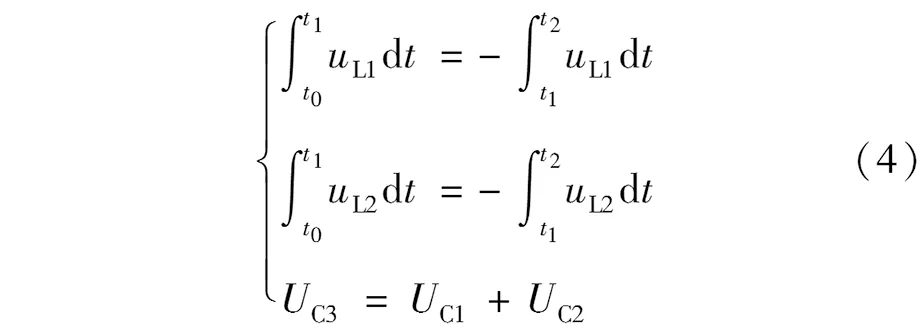
結合圖1(b)和圖1(c)，式(4)可化簡為式(5)的形式。

由式(5)可得：

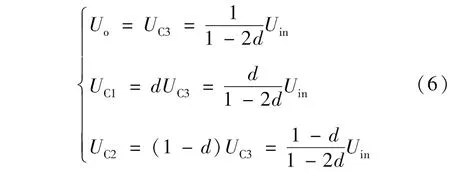
根據式(6)可知該變換器的電壓增益為1/(1-2d)，由理想變換器的輸入輸出功率守恒可得輸入電流Iin為

(7)

式中:Io—負載電流。

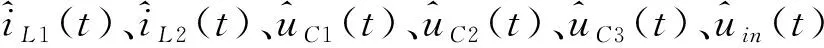
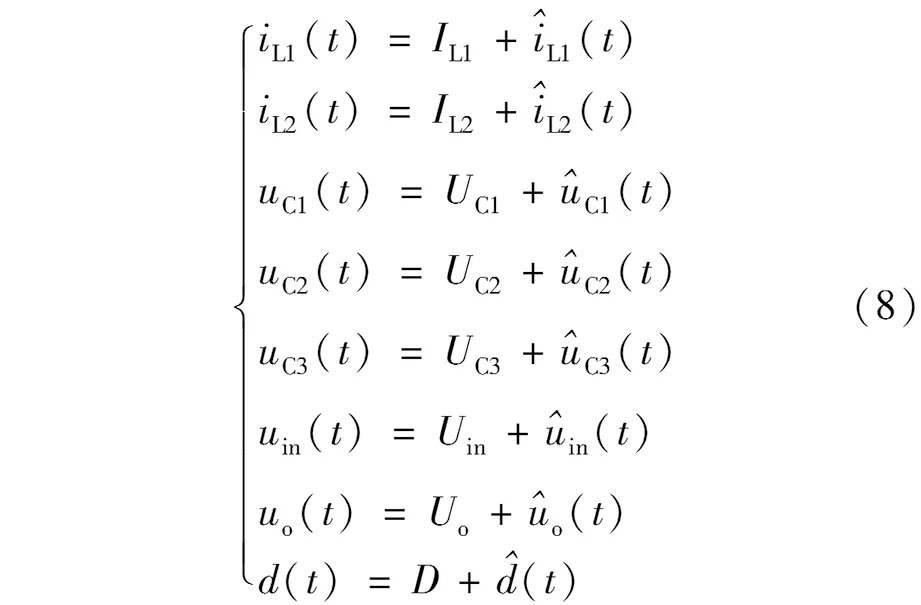
根據狀態空間平均法由式(3)和式(8)可得變換器的小信號狀態模型，如式(9)所示。

根據式(9)所示的變換器小信號狀態模型，可分別求得從輸出到輸入的傳遞函數以及從輸出到控制的傳遞函數，進而可設計變換器的控制策略并進行穩定性分析。

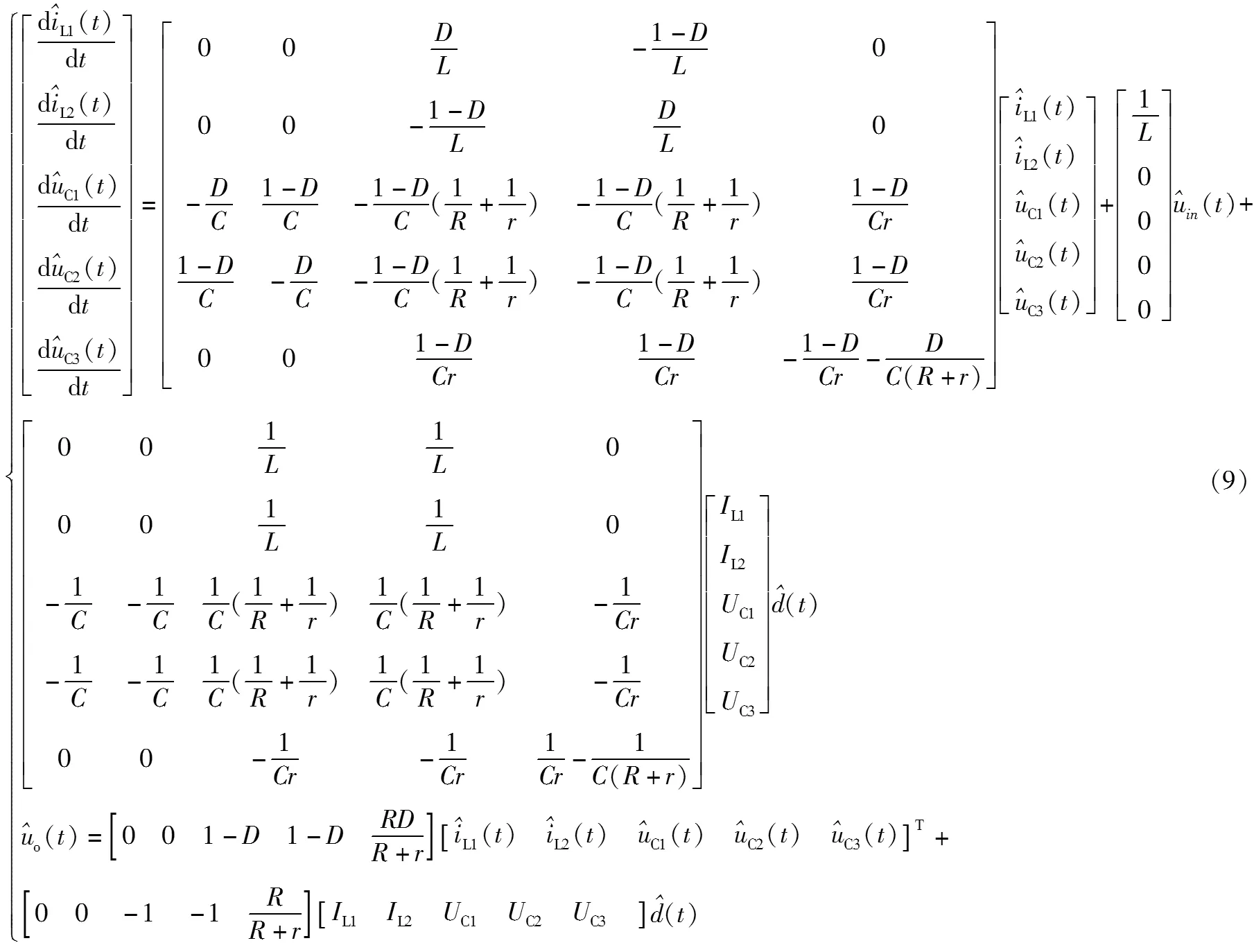
3 仿真驗證與分析

根據圖1(a)在MATLAB/SIMULINK中搭建該變換器的仿真模型(見圖4)，并將其輸出結果與數學模型計算結果進行對比(見圖5)，進而驗證所建數學模型的正確性。

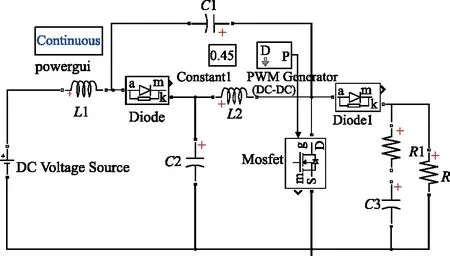
圖4 兩電平準Z源直流變換器仿真模型

相關仿真參數如下：輸入電壓Uin=40 V，占空比d=0.45，電感L1=L2=400 μH，電容C1=C2=C3=470 μF，寄生電阻r=0.01 Ω，負載電阻R=100 Ω。

由圖5可知，變換器數學模型與仿真模型結果曲線的變化趨勢基本一致，并且各穩態輸出結果(輸出電壓、電感電流、電容電壓)基本相同，證明了所建立數學模型的正確性和有效性。

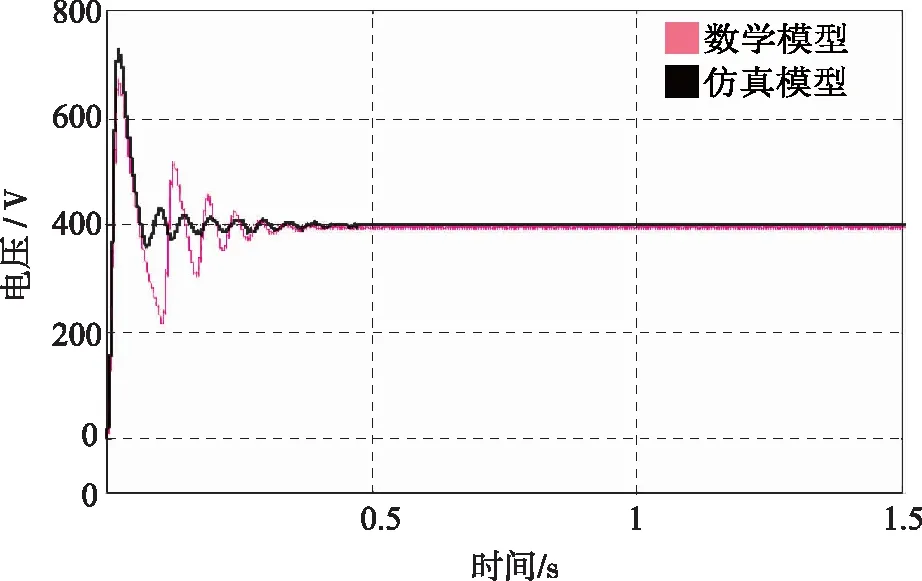
(a)輸出電壓Uo

4 結論

本文對兩電平準Z源Boost直流變換器建立了數學模型，包括平均狀態模型與小信號狀態模型。該變換器的電壓增益為1/(1-2d)。從仿真結果可知，該變換器數學模型與仿真模型結果曲線的變化趨勢基本一致，并且各穩態輸出結果基本相同，證明了所建立數學模型的正確性和有效性。