磁等離子體動力推力器加速機理研究與仿真①

趙博強，李 永，周 成，王 戈，王寶軍，叢云天

(北京控制工程研究所，北京 100094)

0 引言

磁等離子體動力推力器(Magnetoplasmadynamic thruster,MPDT)利用大電流電離推進劑并注入能量，利用磁場和電場來加速等離子體而產生推力。MPDT屬于電推進家族中的電磁推進，與靜電推進相比，能夠更容易做到大推力和大功率，并且效率更高。由國內外已發表的研究成果可知，MPDT的功率可達2 kW～11 MW，比沖范圍2000～11 000 s，效率可達30%～70%。

目前，開展MPDT研究的機構有美國普林斯頓大學、NASA格倫研究中心、蘇聯能源設計局、火炬設計局等。這些單位開展了最大功率達數兆瓦的大功率MPD推力器研究[1]。但迄今為止，附加場磁等離子體推力器并沒有達到令人滿意的效率和比沖。研究認為，這是由于兩個方面的原因：附加磁場的均勻程度、形狀、強度都沒達到推力器最佳工作的參數；等離子體在推力器中的加速機制和損耗機制并未完全掌握。其中，加速機理是制約推力器研究最重要的一方面。

磁等離子體動理推力器的推力理論目前還不成熟，相關的推力產生機理還不明確。針對推力器的試驗結果有一些經驗、半經驗公式。FRADKIN，MYERS等[2-3]分別提出了基于經驗的推力公式。MIKELLIDES等[4-5]基于磁流體力學方程推導了推力器的仿真程序，利用MACH2代碼仿真了推力器。結果表明，利用磁流體方法可較好地仿真出推力器的工作狀況。雖然目前根據經驗和實驗總結出的公式在一定情況下能夠和實驗結果相吻合，但并不能完全準確地描述推力器的工作情況。同時，經驗公式不能反映推力器內部的加速機制，還需要進一步利用等離子體理論推導。文獻[6]和文獻[7]中，提出了一些利用磁流體和粒子模擬方法進行等離子體仿真的工作。文獻[6]利用磁流體方程，對NASA的100 kW推力器進行了仿真，提出了一種基于密度的中心迎風求解格式，取得了不錯的效果。文獻[7]利用PIC/MCC方法，對自身場的推力器放電情況進行了研究。從上述文獻可看出，目前MPD的仿真研究主要集中在推力器的幾何尺寸與推力的關系，以及數值求解方法的研究上，而就磁場對等離子體的研究較少。現階段推力器中磁場強度不是很高，仿真磁場對推力器的影響還不多。隨著超導型磁等離子體推力器的出現，超導線圈極大地提高了附加磁場的強度[8]。研究附加磁場對推力器的影響就變得更加重要。

本文利用磁流體方程組，對磁等離子體動力推力器進行建模，提出了等離子體在磁場中電導率各向異性的建模方法，利用電導率模型，將磁場和等離子體耦合起來，從而對不同強度磁環境下的推力器進行仿真。

1 等離子體物理理論

分析等離子體主要有兩種方法：磁流體方法和動理學方法[9]。由于磁等離子體推力器中等離子體濃度極大，滿足磁流體方程連續性假設。磁流體方程組由連續性方程、動量方程、能量方程和麥克斯韋方程組和歐姆定律組成[10]。

連續性方程形式如下：

(1)

式中ρ為等離子體的密度，ρ=∑Nm;N和m分別為粒子的數密度和粒子的質量；V為等離子體的速度矢量。

對于MPDT而言，假設在工作中推進劑完全電離，在計算中需要考慮離子和電子兩種成分，對每一種成分都需要一個方程來對應。

根據文獻[11]中記載，在距離陰極出口幾毫米地方的等離子體就已經完全電離，且在文獻中觀察到等離子體電離率也遠大于Saha方程計算結果[11]。本文的仿真區域中等離子體電離度很高，仿真時為了簡化計算，忽略了推進劑電離過程，認為等離子體已經完全電離。

動量方程形式如下：

(2)

式中I為單位張量；p為壓力；τ為粘性應力張量。

能量方程形式如下：

(3)

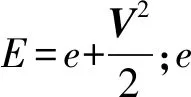
在不考慮多種組分的情況下，上述方程組包含5個方程、6個物理量，分別是ρ、V、T和p。為使方程組閉合，還需要補充等離子體的狀態方程。假設等離子體為理想氣體，那么狀態方程可表示為

p=p(ρ,T)=2NkT

對于單流體模型，假設離子溫度和電子溫度相同，雙流體模型認為離子和電子處于不同的溫度。

在等離子體中，電磁場由麥克斯韋方程組來計算：

式中ρq為電荷密度；E和B分別為電場矢量和磁場矢量；J為電流密度矢量，由歐姆定律給出。

J=σ(E+u×B)+ρqu

(4)

而電磁場對流體的作用力根據洛倫茲力公式計算：

F=ρqE+J×B

(5)

2 磁化等離子體的電導率

當一個離子和一個電子碰撞時，認為離子和電子之間只存在庫侖力作用，假設離子使得電子運動方向偏轉90°時，認為離子和電子發生了碰撞，離子和電子之間的庫侖力為

(6)

式中r0為碰撞截面半徑。

假設電子和離子之間是圓周運動，電子大約偏轉1/4個圓周，整個過程運動時間為

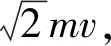
碰撞截面為

(7)

電子和離子碰撞頻率為

(8)

等離子體的電阻率為

(9)

以上方程都是基于大角碰撞產生的電阻率。實際上，由于庫侖力是長程力，小角碰撞可能更加頻繁。斯必澤證明，方程應乘上一個修正因子[10]。

(10)

(11)

對于麥克斯韋分布的電子，可用KT/m來代替v2，因此有

(12)

(13)

根據以往的試驗和文獻結果，lnΛ是一個和電子溫度和濃度有關的物理量，在電子溫度和濃度變化范圍很大時，lnΛ變化范圍比較小。因此，這里為了計算方便，假設lnΛ=10，對于MPDT中的等離子體，這個結果認為足夠精確[10,12]。同時，MPDT中等離子體電子溫度KT≈4 eV可計算得到，等離子體碰撞頻率約為4.4×107s-1，等離子體的電阻率為5.284 4×10-5Ω·m。

上面公式為傳統的無磁場條件下等離子體的電導率，在存在磁場的情況下[12]，等離子體電導率為

(14)

其中

2.1 在弱磁場條件下ωce τ≤1

在弱磁場下垂直方向的電導率為

(15)

其中

霍爾電導率為

(16)

其中

平行磁場方向電導率為

σ‖=σ

(17)

(18)

2.2 在強磁場條件下ωce τ≥1

在強磁場下垂直方向的電導率為

(19)

其中

lnΛ3=lnΛ(ve3)

霍爾電導率為

(20)

式中c為光速。

平行磁場方向電導率為

σ‖=σ

(21)

3 AF-MPDT仿真方程組

磁等離子體推力器的仿真環境在低真空下進行，仿真時，電子和離子溫度不相同。因此，利用雙流體MHD方程組，對MPDT進行仿真[13-16]。

首先是電子和離子的質量守恒方程組：

(22)

(23)

式中ne和ni分別為電子和離子的密度；ue和ui分別為電子和離子的速度；m和M分別為電子和離子的質量。

MPDT工作條件是低真空情況下，且在推力器放電腔體內推進劑完全電離，假設在仿真區域內部為完全電離等離子體，只存在電子和離子。因此，連續性方程有兩個。

電子和離子的質量守恒方程組為

(24)

(25)

式中Mei為電子離子動量交換項。

式中νei為電子離子碰撞頻率。

電子和離子的能量守恒方程組為

(26)

(27)

其中

4 仿真

推力器模型如圖 1所示。其中，左上角不規則區域為推力器放電腔和羽流區，深入放電腔的為陰極，放電腔左邊壁為陽極。右側矩形區域為磁線圈。剩余部分為仿真空間中磁場的自由空間。

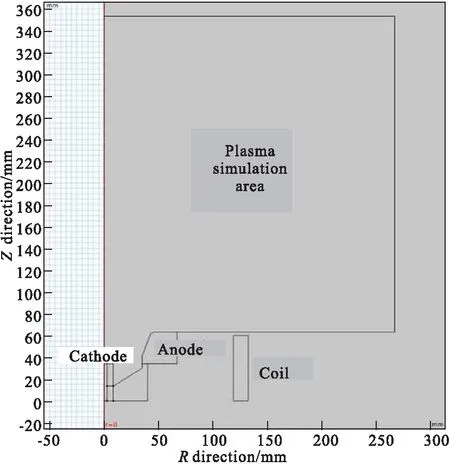
圖1 磁等離子體動力推力器模型

由于磁流體方程組是非線性的方程組，無法求解方程組的解析解，且在強磁場、高密度等離子體中，等離子體狀態變化非常劇烈。因此，需要使用高分辨率的求解格式來對方程組進行數值求解[17-20]。

下面是對推力器不同工作情況下的仿真分析。工作條件為推進劑質量流量40 mg/s，工作電流320 A，中心磁場強度為1.54 T，仿真得到的工作電壓236 V，離子速度約為46 800 m/s，計算得到推力約為1.87 N，功率約為75.5 kW。計算結果如圖2所示。

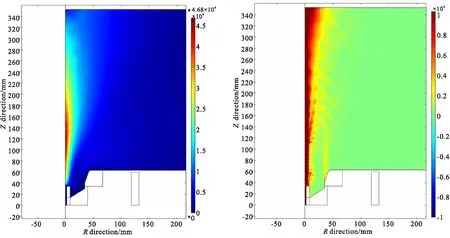
(a)Ion velocity under central magnetic field strength 1.54 T (b)Current density at 1.54 T for central magnetic field strength

推進劑質量流量40 mg/s，工作電流320 A，中心磁場強度為0.66 T，仿真得到的工作電壓160 V，離子速度約為43 000 m/s，計算得到推力約為1.72 N，功率約為51.2 kW。計算結果如圖3所示。

(a)Ion velocity under central magnetic field strength 0.66 T (b)Current density at 0.66 T for central magnetic field strength

推進劑質量流量40 mg/s，工作電流320 A，中心磁場強度為0.53 T，仿真得到的工作電壓152 V，離子速度約為42 000 m/s，計算得到推力約為1.68 N，功率約為48.6 kW。計算結果如圖4所示。

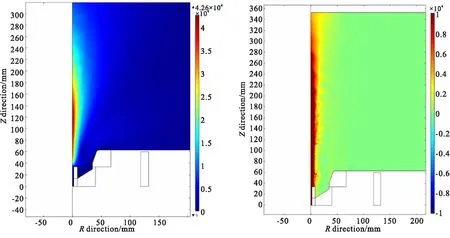
(a)Ion velocity under central magnetic field strength 0.53 T (b)Current density at 0.53 T for central magnetic field strength

推進劑質量流量40 mg/s，工作電流320 A，中心磁場強度為0.2 T，仿真得到的工作電壓120 V，離子速度約為34 000 m/s，計算得到推力約為1.36 N，功率約為38 kW。計算結果如圖5所示。

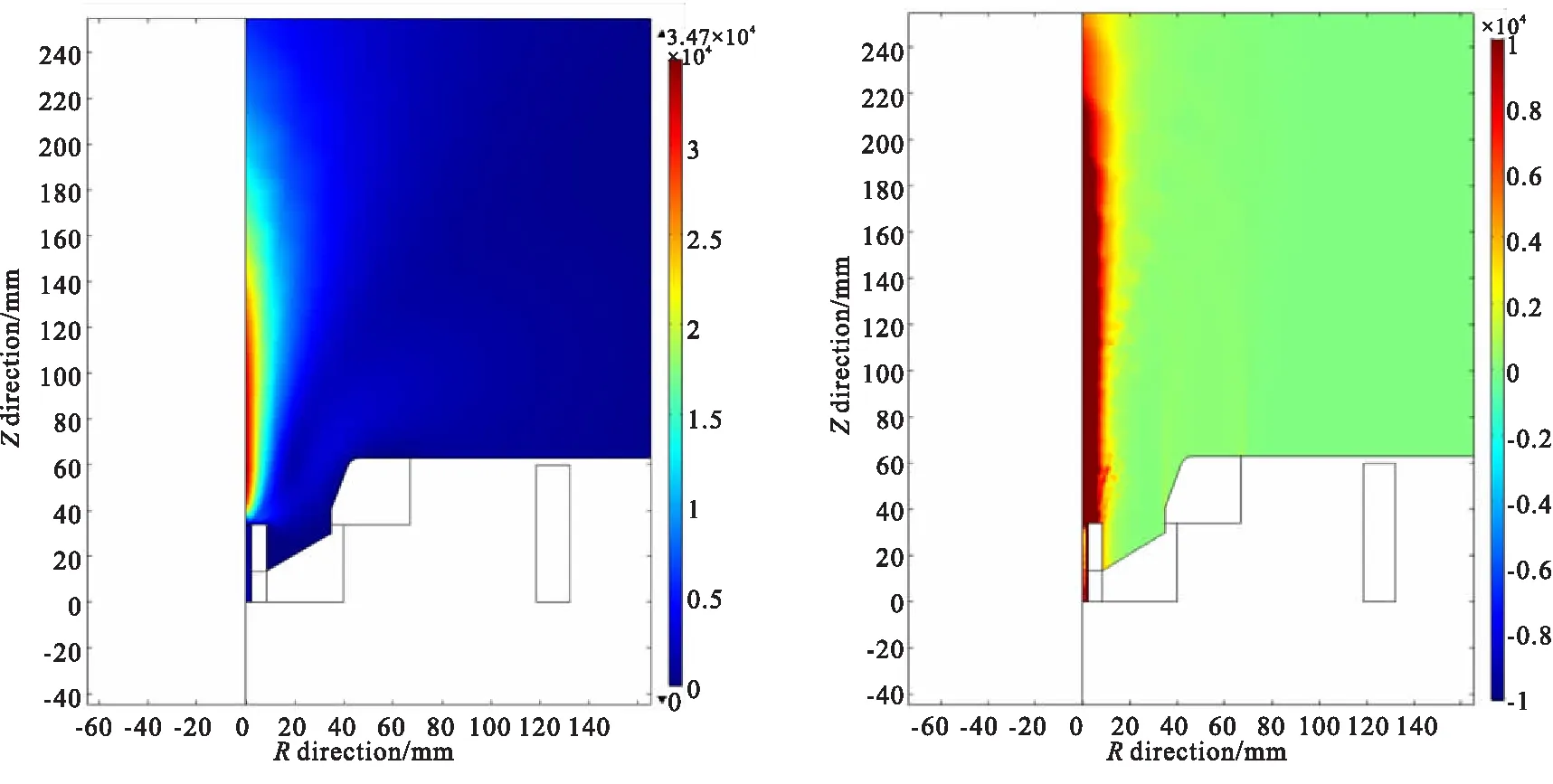
(a)Ion velocity under central magnetic field strength 0.2 T (b)Current density at 0.2 T for central magnetic field strength

仿真模擬了在恒定電流的情況下，通過調節推力器的附加磁場強度，得到不同工況下推力器參數。仿真了中心磁場1.54、0.53、0.66、0.2 T情況下推力器的工作情況。表1為仿真結果的匯總。

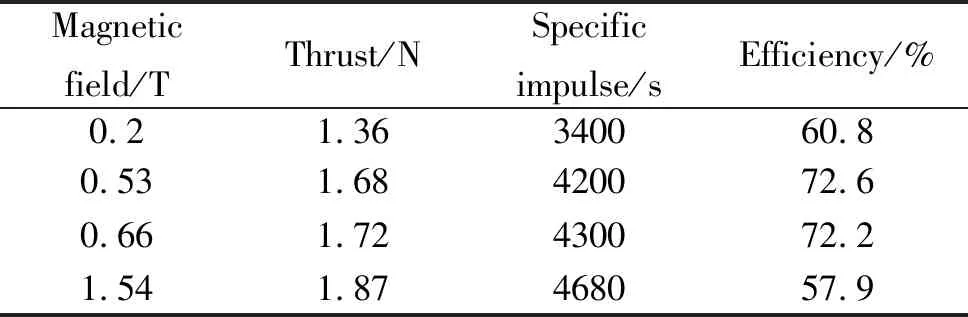
表1 仿真結果

根據理論分析[21-22]，在磁場中，等離子體電導率出現各項異性，在推力器的軸向方向上電導率最大，電子和離子主要集中朝這個方向運動。

通過仿真可看出，在電流恒定的情況下，增強磁場，可使得電壓增大，推力器工作的總功率增加，比沖和推力都增加。隨著磁場強度的增加，推力器的效率會隨著磁場的增加，先升高、再降低，說明磁場在0.6 T附近是當前推力器最好的磁場強度范圍，適當的磁場能夠提高能量注入的效率，低強度的磁場不能很好地約束等離子體，而過強的等離子體會導致等離子體電阻過大，能量損耗過大，也會導致效率降低。因此，磁場強度還需要和推力器尺寸相匹配，才能得到更好的效果。

根據理論和實驗仿真還可推斷出，在電壓恒定的情況下提高磁場，可使推力器的電流密度降低，功率下降，等離子體獲得的能量降低，但等離子體仍能保持較高的比沖，且電流降低可減少在熱量在推力器總的產生，可減小陰極的燒蝕，并減輕電源的工作負擔，對提高推力器的工作壽命和可靠性都有好處。

5 結論

本文通過磁流體力學方程組和等離子體理論，對磁等離子體推力器的磁流體模型進行推導，通過磁化等離子體電導率模型，將磁場和等離子體耦合起來，建立了在不同強度磁場環境下的磁流體模型，并對該模型進行了仿真。

通過仿真結果可看出，推力器比沖和電壓隨著磁場的增加而增加，這個結論和文獻中是相符的。通過對推力器加速機理進行了分析，認為由于磁場導致等離子體電阻率增加，導致了更多的能量注入，且磁場對等離子體運動有約束作用，使得更多的等離子體沿著軸向噴出，從而提高了推力器的比沖和功率。在磁場增強之后，導致效率降低的問題還需要進一步的研究。

本文利用磁流體模型和電導率模型，對磁等離子體動力從理論上初步分析了磁場對推力器的影響，在工程上可為推力器的設計提供進一步的仿真依據，為以后的推力器設計和優化提供參考。