一種高效的關于兩方集合并/交集基數的隱私計算方法

程 楠, 趙運磊

1. 復旦大學 軟件學院, 上海210203

2. 復旦大學 計算機科學技術學院, 上海210203

1 引言

在當今的數字時代, 越來越多的公司通過收集數據, 并基于自身的合理需求加以利用而獲得了相當的回報, 例如: 基于消費者使用偏好等數據, 互聯網公司研發出推薦系統, 個性化地提供互聯網產品或服務;基于用戶歷史瀏覽數據并結合智能算法, 廣告商實現了精準營銷. 這一回報也就反過來激發出更多的數據采集需求, 在這個過程中, 用戶的個人隱私必然越來越難以被保護, 因此數據隱私計算技術就變得越來越重要: 于用戶而言, 這一技術能在最大限度地保護他們的隱私的同時提供便捷; 于商家而言, 這一技術可以在幫助他們避免核心數據的泄漏的前提下最大限度地發揮其核心數據的價值. 在全球日益重視數據安全的背景下, 各大國家已紛紛立法保護數據隱私(如美國的HIPAA、COPPA、GLBA、歐盟的DPP), 數據隱私計算技術逐漸成為當前學界研究的一個熱潮.

兩方PSI (Private Set Intersection) 問題是關于安全兩方計算模型中最基礎的一類問題. 在兩方PSI問題中, 我們用Alice 和Bob 表示參與方, 并假設其分別持有任意長度字符集合X 和Y. 在一系列的交互完成后, 我們要求至少有一方能得到雙方的交集X ∩Y, 并且每一參與方都不能獲知關于對方集合元素的任何其它知識. 我們可以使用基于不經意傳輸(Oblivious Transfer, OT) 的協議[1–4]來高效地解決這個問題.

兩方PSU/PSI-CA (Private Set Union/Private Set Intersection Cardinality) 問題是兩方PSI 問題的延伸, 它要求最終計算出|X ∪Y|/|X ∩Y|, 且在此過程中不泄漏任何其它的信息(包括自己的任何一個元素信息及自己的集合大小). 該問題對應于現實中許多隱私計算場景, 例如: 在社交網絡中, 兩個用戶可以在不泄漏自己具體好友信息的情況下比較其相同好友的比例, 來計算社交關系重合度; 在健康領域, 持有私有基因數據的客戶可以放心地與公共風險基因數據庫交互, 從而得知自己感染某種疾病的概率; 本文就是要討論解決PSU/PSI-CA 問題的相關協議.

一般而言, 理論上所有的隱私計算問題都可以用通用的的安全計算協議來解決(如GMW 協議[5]、混淆電路[6]). 但這些通用的方案需要較高的計算和通訊代價. 因而, 對于具體的安全計算問題, 我們通常使用專用的高效協議. 具體地, 對于解決PSU/PSI-CA 問題的協議而言, 從輸出結果的精確程度來分類, 我們分為如下兩類.

(1) 第一類協議為完美計算協議, 它輸出精確的結果. 以文獻[7–12] 等工作為例, 它使用模糊多項式評估方法, 選定一個多項式來代表輸入集合并通過同態加密技術來合并評估集合的交. 但是這一類的協議使用大量的公鑰原語, 因此, 即使在半誠實模型下, 它們實際執行時的資源消耗也非常大.

(2) 第二類協議為不完美計算協議, 它的輸出結果容許一定的誤差. 面對數量級較大的數據時, 該類協議由于能夠在效率與可用性之間取得較好的平衡, 因而在現實中得到更廣泛的應用. 例如:

? Egert-Fischlin 協議[13]通過將其中一方的布隆過濾器的每一位用ElGamal 公鑰系統[14]進行加密, 從而實現隱私計算. Egert-Fischlin 協議的優點在于非平衡性, 協議的主要計算開銷集中于其中一方, 因此它適合于服務器-客戶端類型的應用場景[13]. 不過因其計算與通信復雜度均為O(n),所以當輸入量級逐漸變大時, 它便難以推廣應用.

? Dong-Loukides 協議[15]基于Flajolet-Martin 技術[16]和OT14技術, 它夠將長度為n 的集合預處理為長度為log(n) 的Flajolet-Martin 概要[16], 因而大大降低了后續使用OT14原語產生的計算開銷. 但該計算必須串行地調用OT14協議, 因此它的通信輪數較多, 網絡環境較差時, 網絡時延影響比較明顯. 此外, 為了提高輸出結果的精確度, 這一協議需要在離線階段對同一個集合生成大量不同的Flajolet-Martin 概要[16], 因此它的哈希成本相對較高. 不過, 實驗數據[15]表明,Dong-Loukides 協議依然是目前解決PSU/PSI-CA 問題最高效的協議之一.

本文側重于不完美計算協議的設計與分析, 因為它能夠在效率與可用性之間取得較好的平衡. 受Dong-Loukides 協議的啟發, 我們提出一種基于預計算OT 模型[17]的方案, 在該方案中, 無論是解決PSU-CA 問題還是PSI-CA 問題, 首先都要進行秘密分享(Secret Sharing), 它分為兩個階段: 即離線階段和在線處理階段. 離線階段中, Alice 和Bob 分別調用Silent-OT 協議[18]交互生成足夠多的偽隨機相關消息對. 在線階段中, 假設Bob 為不經意傳輸的發送方, 則Bob 根據之前已生成好的偽隨機相關消息對跟自己真正要發送的消息做掩碼運算, 之后發送給Alice, Alice 直接通過離線階段收到的消息進行解密.這兩步操作完成后, Alice 和Bob 將分別得到關于HW(BFA∨BFB) 的秘密分享SA和SB. 而后:

? 在解決PSU-CA 問題的子協議中, 不妨設Alice 為最終結果的輸出方, 那么此時Bob 需將其秘密分享SB發送給Alice, 則Alice 將兩個秘密分享SA和SB合并, 最終輸出估算的兩個集合的并集的勢.

? 在解決PSI-CA 問題的子協議中, Alice 和Bob 還需要額外執行一個同態計算協議, 完成協議執行后, 輸出方輸出估算的兩個集合的交集的勢.

由于進行秘密分享的離線過程的計算可以事先完成, 而在線階段的計算只進行高效的掩碼運算, 因此我們的秘密分享非常高效. 而且無論是對應PSU-CA 還是PSI-CA 問題的子協議, 后續的開銷都很小. 因此同之前大部分基于公鑰計算的協議相比, 我們的方案帶來了較大的效率提升.

2 預備知識

在本文中, 對于一個有限集合X 我們用符號|X| 表示它的勢, 符號|X|?表示集合勢的近似整數估值. 符號BFX表示對應集合X 的布隆過濾器. 表達式r ←$S 表示從有限集合S 中隨機均勻選取一個元素r. 對于正實數x, 符號?x?表示x 向下取整的值. 對于二進制串B, 符號HW(B) 表示B 上1 的個數.

2.1 布隆過濾器

在我們的方案設計中, 我們首先使用布隆過濾器(Bloom Filter, BF) 對集合進行預處理, 布隆過濾器被Bloom[19]首次提出, 他將一個集合中的每一個元素通過若干哈希函數到映射到一個二進制串, 最終得到一個輕量級的二進制串, 這就是布隆過濾器. 它主要被用于檢測一個元素是否隸屬于某些數據集合. 當構建某個數據集X 的布隆過濾器時, 首先我們會選定生成參數: 包括k 個相互獨立的哈希函數, 該布隆過濾器所預設的容量d, 錯誤率e. 此外初始化一個全為0 的二進制串BFX, 設其長度為m, 繼而使用k個彼此獨立的哈希函數hi: {0,1}{1,··· ,m} (其中i ∈{1,··· ,k}) 將集合中的每一個元素映射到某個正整數, 若BFX對應位置的值為0, 則將其更改為1. 任何第三方若要檢測某個元素a 是否位于集合X中, 首先可使用對應的哈希函數組計算a 所有的映射值, 接著檢查BFX上對應位置是否全為1, 是的話說明元素a 很可能位于集合X 中, 否則說明a 一定不是集合X 中的元素.

圖1 展示了對集合{x,y,z} 生成布隆過濾器及進行元素檢測的圖示[20], 其中哈希函數組的個數為k =3, 最終生成的布隆過濾器長度m=18, 其中元素w 經過檢測可知不在集合{x,y,z} 中, 因為該元素的某個哈希值對應的位置為0.

由于哈希碰撞的存在, 布隆過濾器存在一定的假陽性檢測. 布隆過濾器的長度m 與哈希函數組的大小k 和其容量大小d 直接相關, 直觀上, 將m 取得很大的話, 哈希的碰撞會減少, 布隆過濾器的檢測錯誤率e 會降低, 但這樣在計算上會降低效率. 根據文獻[21], 使用如下公式對k 和m 進行約束, 我們可以在布隆過濾器的計算效率與錯誤率之間取得較好的平衡.

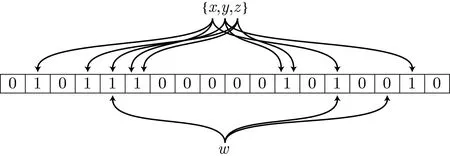
圖1 布隆過濾器生成及元素檢測示例Figure 1 Example for Bloom filter generating and membership checking

對于一個集合X, 我們可以用如下公式[22]估算它的勢:

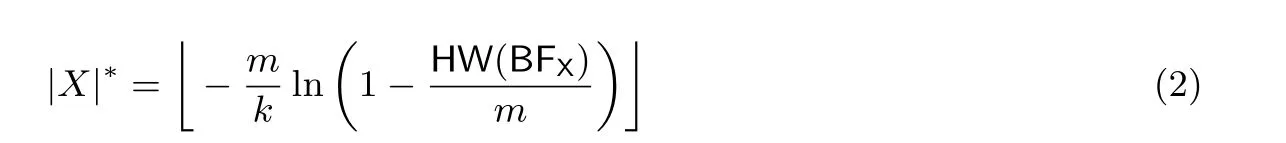
對兩個不同的集合A 和B, 設其使用同樣的參數分別生成BFA,BFB, 令BFA∨BFB表示BFA和BFB按位求或的二進制串, 則估算兩個集合A, B 的并交集大小的公式分別為:

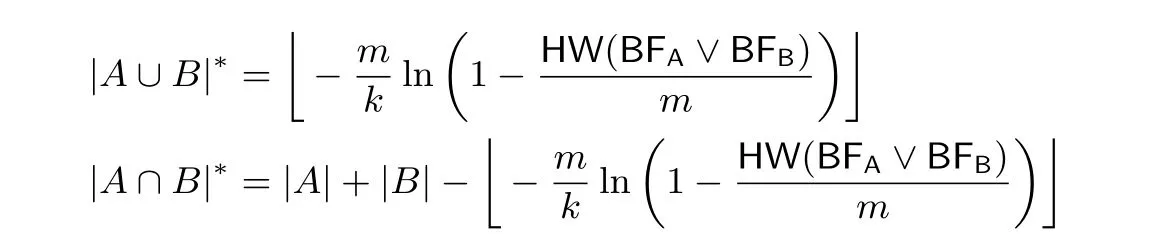
綜上所述, 布隆過濾器可以被用來估算兩方集合的并集的勢, 不過這隱含地意味著它們都知曉對方集合的勢的上界.

2.2 Paillier 加密系統

本文在解決PSI-CA 問題的協議中使用了Paillier 加密系統[23], 它是一個具有同態性質的公鑰加密系統, 分為密鑰生成算法、加密算法和解密算法, 如下所示(其中符號Z?n表示集合, 它滿足Z?n= {x ∈Zn:gcd(x,n)=1}).

密鑰生成算法:

Paillier 加密系統的安全性基于判定性復合剩余類假設(Decisional Composite Residuosity Assumptio, DCRA). 一般認為, 當n 足夠大時, 對攻擊者而言, 不知道n 的素因式分解, 判定性復合剩余問題是困難的. 該加密系統具備加法同態性:

2.3 不經意傳輸

圖2 離線-在線框架Figure 2 Offline-online framework

3 兩方PSU/PSI-CA 協議

本節中, 我們將給出解決PSU-CA 問題和PSI-CA 問題的協議構造和相關證明. 首先, 我們分別給出解決PSU-CA 問題和PSI-CA 問題的兩個協議構造(3.1 節), 然后分別給出它們的正確性證明(3.2 節),最后我們給出基于模擬的安全性證明(3.3 節).

3.1 協議構造

在兩個協議執行中, 我們不妨設兩方參與者分別為Alice 和Bob, 分別持有集合A 和B. 我們的協議要求兩方輸入兩個結構相同的布隆過濾器, 其生成過程如下:

(1) Alice 和Bob 約定足夠大的容量d, 輸入錯誤率e, 由公式(1)并經過取整計算, 分別得到所使用哈希函數個數k 及所要生成的布隆過濾器的長度m.

(2) Alice 和Bob 分別使用相同的k 個哈希函數對他們的輸入集合A,B 進行處理, 最終獨立地得到各自的布隆過濾器BFA,BFB.

此后在協議描述中我們直接將BFA,BFB作為輸入, 不再贅述該生成過程. 無論是PSU-CA 協議或者PSI-CA 協議, Alice 和Bob 在離線階段執行相同的操作, 如下所示.

3.1.1 離線階段

3.1.2 在線階段

無論是計算PSU-CA 問題還是PSI-CA 問題, Alice 和Bob 首先都要執行秘密分享協議, 如圖3 所示.

圖3 秘密分享協議Figure 3 Secret sharing protocol

(i) 首先Alice 和Bob 執行兩輪交互, 具體步驟如下:

圖4 同態計算協議Figure 4 Homomorphic computing protocol

3.2 正確性分析

故原命題得證.

3.3 安全性分析

目前兩大主流安全模型是半誠實模型(Semi-Honest Model) 和惡意模型(Malicious Model)[27]. 在半誠實模型下, 敵手會記錄協議交互過程中的所有數據, 并嘗試提取其它參與方的秘密信息. 在惡意模型下, 敵手會以任意的方式偏離協議的執行來進行破壞或窺探.

本文所涉及的所有安全協議都是在半誠實模型下[27]證明的. 一般而言, 當構建一個隱私計算協議時,我們會首先在半誠實模型下構建. 雖然半誠實模型比惡意模型的假設要弱, 但實際上, 現實的業務部署都必須符合某些安全法令的制約, 這保證了半誠實模型下的協議依然有廣泛的應用前景.

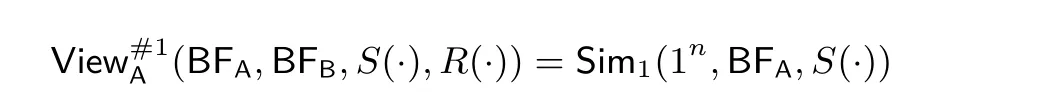
定理1 存在一個概率多項式時間的模擬器Sim1使得對于所有的安全參數n 滿足2n> |BFA| 和輸入BFA, 有其中S(·),R(·) 分別表示Alice 和Bob 的偽隨機相關預設消息,(BFA,BFB,S(·),R(·)) 表示在協議#1 執行中Alice 的視圖.

算法1: Alice 的模擬算法Input: 1n,BFA,{(R01,R11),··· ,(R0m,R1m)}Output: Sim1(·)1 隨機選取¨r ←${0,1}m, 作為Bob 第一輪發送給Alice 的輸入模擬.2 Alice 真實按照協議執行計算{(M0i,M1i)}i∈[m] 和S1, 模擬第二輪的輸出.

證明: 我們用算法1 描述Sim1(·).

在算法1 的第一步中, ¨r 在 {0,1}m上隨機均勻選取, 而在真實的執行中, ¨r = {d1⊕(1 ?BFB[1]),··· ,dm⊕(1 ?BFB[m])}, 因為di為隨機選取, 因此模擬的Bob 輸入¨r 與真實協議執行中Bob發送給Alice 的¨r 是計算不可區分的. 在第二步中, 由于上述模擬算法完全按照真實協議執行的步驟, 因此模擬的輸出與真實的輸出同分布.

綜上所述, 上述Alice 的模擬算法能模擬協議#1 執行中Alice 的交互視圖. 因此定理得證.

定理2 存在一個概率多項式時間的模擬器Sim2使得對于所有的安全參數n 滿足2n> |BFA| 和輸入BFA,BFB, 有

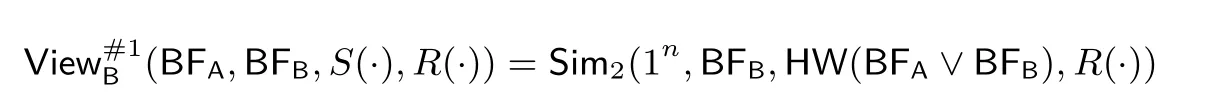
其中S(·),R(·) 分別為Alice 和Bob 的偽隨機相關預設消息, View#1

B (BFA,BFB,S(·),R(·)) 為上述協議

#1 中Bob 的交互視圖.

算法2: Bob 的模擬算法Input: 1n,BFB,HW(BFA ∨BFB),R(·)Output: Sim2(·)1 Bob 輸入R(·) 和BFB 之后, 按照協議#1 的真實執行過程輸出Bob 第一輪的輸出模擬¨r.2 對于?i ∈[m], 選取ri ←${0,1}n. 選取MBFB[i]i = ri ⊕Rdii . 計算S1 = (2n +m ?HW(BFA ∨BFB)?(∑m i=1 ri) mod 2n)) mod 2n. 則上述{(M0i,M1 i)}i∈[m],S1 即為對第i ←${0,1}n；令M1?BFB[i]二輪Alice 輸入的模擬.3 真實地按照第三輪的執行計算S2 作為對S2 的模擬輸出.

定理3 存在一個概率多項式時間的模擬器Sim1使得對于所有的安全參數λ 滿足2λ>m 和所有的輸入(S(·),R(·),|A|,|B|,m,k,(pk,sk)), 有

算法3: Alice 的模擬算法Input: 1λ,S(·),|A|,f(·)Output: Sim1(·)1 令S?1 := Encpk(0), 模擬Alice 第一輪輸出S1 的模擬.2 令?S?:= Encpk(0), 作為第二輪中?S 的模擬輸出.3 隨機選取β ←$(0,1) (表示從該區間選取小數點后四位的小數), 計算? = |A|?f(·)+β, 然后計算Dec ?S?= p·m ?·k exp m, 模擬Bob 的?S 的解密值T?, 最后輸出f(·).

算法4: Bob 的模擬算法Input: 1λ,R(·),|B|,BFB Output: Sim2(·)1 令 ?S1?:= Encpk(0), 模擬協議第一輪Alice 的輸入 ?S1 的模擬.2 令?S?:= Encpk(0), 作為第二輪?S 的模擬輸出.

證明: 我們用算法4 描述Sim2. 由于Bob 只需要模擬由同態加密保護的消息, 由于Paillier 加密系統抗選擇明文攻擊(Chosen Plaintext Attack, CPA) 的特性, 因此其能夠完美模擬真實協議中的消息. 那么通過上述給定輸入1λ,R(·),|B|,BFB, 該構造能夠模擬協議#2 中Bob 的交互視圖, 故定理得證.

綜上所述, 結合定理1 和定理2, 我們使用模擬的方式證明了協議#1 在半誠實模型下的安全性. 結合定理1–4, 我們證明了協議#2, 即解決PSI-CA 問題的協議在半誠實模型下也是安全的.

4 性能評估

本節我們從理論分析和具體實驗兩個方面, 將我們的協議同Dong-Loukides 協議[15]在不同指標上進行比較, 來說明我們的協議在總體上有較好的性能, 并且適用于更廣泛的應用場景.

4.1 理論評估

表1 為定性的性能對比. 其中N 為集合的大小, k1為生成布隆過濾器的哈希函數個數, k2為生成Flajolet-Matin 概要所需的哈希函數個數. 且k1?k2. 其中的哈希開銷一列是指預處理階段的哈希開銷,在Dong-Loukides 協議中即指將集合轉化為Flajolet-Martin 概要[16]的哈希開銷(為了提高協議的計算結果準確度, 一般需要將k2設置為比較大的常數), 而在協議#1,#2 中, 指布隆過濾器生成時的哈希開銷(此時k1=?, r 為錯誤率).

從表1 可以看出協議#1 和協議#2 的通信輪數及冪指數運算開銷均為為常數, 此外可知, 協議#1和協議#2 除了通信量比Dong-Loukides 協議要大之外, 其它方面都更好. 且當一個數據集的數據有微小更新時, 在Dong-Loukides 協議中也需要幾乎重新生成Flajolet-Matin 概要, 這一不足也大大限制了Dong-Loukides 協議可能適用的應用場景. 此外, Dong-Loukides 協議的離線預計算依賴于具體的數據集,而我們所調用的Silent-OT 協議[18]不依賴于任何具體的數據集, 因此它具有更廣的應用場景.

表1 理論對比Table 1 Theoretical comparison

4.2 實驗評估

我們分別對三個協議做了實現(https://github.com/athenKing/PSU-PSI-CA) 來對比他們具體的性能表現, 三個協議都通過C++ 完成實現, 進行測試的平臺搭載了2.9 GHz double core Intel-core I5 處理器和16 GB 1867 MHz DDR3 內存. 該測試在LAN 網絡環境下完成, 網絡時延較低. 在Dong-Loukides協議的實現中, 設置安全參數λ = 128, 設置獨立哈希函數的個數k2為4096, 輸出的Flajolet-Martin 概要[16]長度設置為32 (其理論上能統計至多232?1 個元素). 協議#1 和協議#2 的實現中, 同樣設置安全參數λ=128, 布隆過濾器的錯誤率設為r =0.05, 三組數據(從小到大) 對應的布隆過濾器最大容量分別設為5000, 50 000, 400 000. 表2 展示了它們在不同數量級輸入下的實際性能比較結果. 其中Nx和Ny表示輸入的兩個集合的大小, PSU/PSI-CA 誤差(%) 表示輸出結果的相對誤差, 即兩個集合并集和交集基數輸出結果相對真實結果的誤差. DL 協議表示Dong-Loukides 協議.

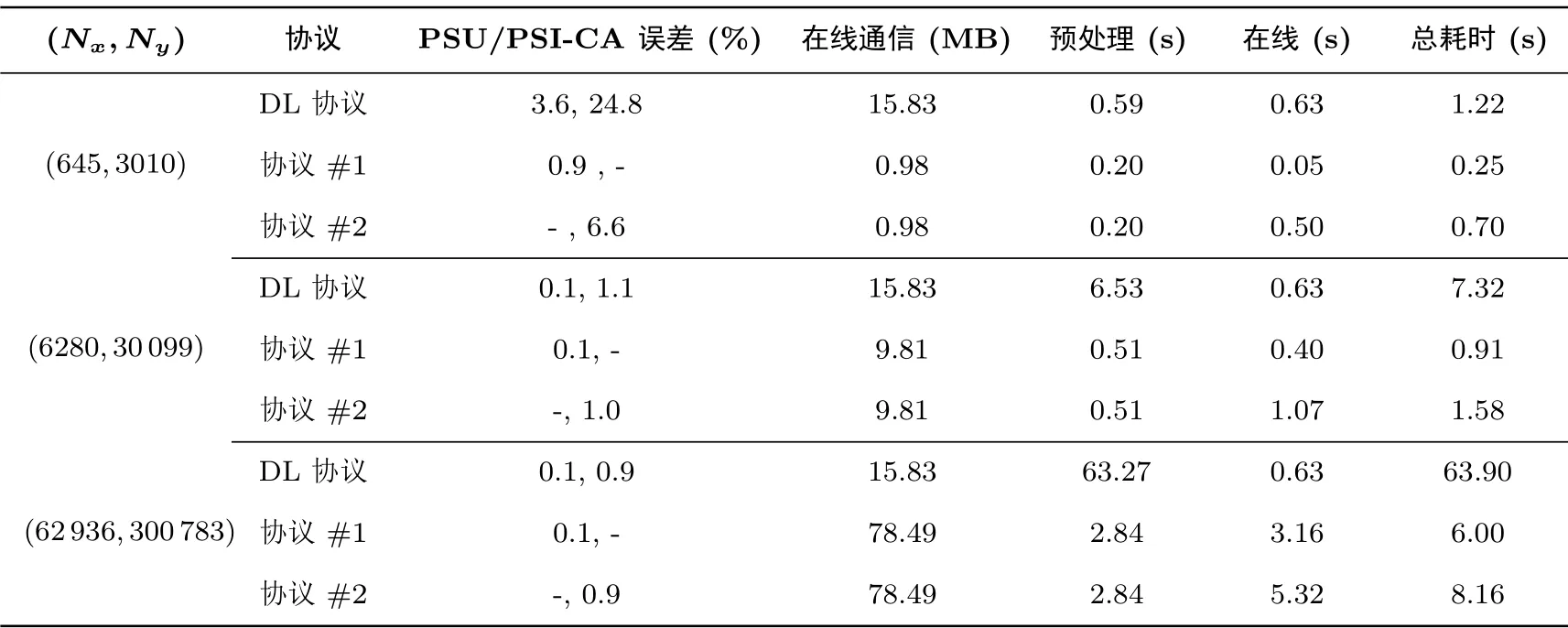
表2 實驗對比Table 2 Experimental comparision

由表2 的實驗結果可知, Dong-Loukides 協議的預處理階段比較耗時, 因此它不適合數據集更新頻繁的場景, 只適用于某些數據永久或半永久化存儲場景下的安全計算. 可以看到, 無論數據集的大小, 相比Dong-Loukides 協議協議#1 和協議#2 的總耗時都更小, 而且當數據集的輸入從小變大時, 這種性能優勢也越來越明顯. 所以, 我們的協議在數據集更新頻繁的計算場景中有比Dong-Loukides 協議更高的計算效率.

5 總結與展望

本文提出一種新的解決PSU/PSI-CA 問題的不完美計算協議, 并在半誠實模型下證明了它的安全性.它使用布隆過濾器對集合預處理, 并混合了OT 預處理[17]和Paillier 同態加密技術[23]. 同最先進的協議之一Dong-Loukides 協議相比, 該協議總耗時更低, 并且有較廣泛的應用場景.

我們的協議不能抵抗惡意的敵手, 因此下一步, 通過結合當前方案和零知識證明[27]的技巧, 我們會嘗試構建一個高效的在惡意模型下[27]可證明安全的協議.