基于遺傳算法的多機型多熱源復雜熱電負荷優化分配方法

李 軍,陳 利,李華東,代書海,魏化雷

(吉林松花江熱電有限公司，吉林 長春 130022)

0 引言

隨著傳統化石能源日益枯竭和全球氣候變暖等問題日益嚴峻，我國必須堅持低能耗、低排放、節約自然資源的低碳經濟模式和可持續發展道路，由此掀起了“開源節流”的新熱潮[1]。熱電聯產機組可以同時生產電負荷和熱負荷，以滿足用戶的不同需求[2]，并且對背壓機組來說，避免了余熱直接排放而造成的冷源損失，是提高火電機組能源利用率的有利手段，特別是在“三北”地區得到了廣泛的應用。熱電聯產機組為了滿足熱用戶的需求，通常采用“以熱定電”的方式運行，因此熱負荷和電負荷之間存在著強烈的耦合[3]。對于廠內多臺機組并列運行的情況，為了實現能源的高效合理利用，如何分配機組之間的熱電負荷成為至關重要的問題。郭民臣等人[4]提出了熱耗變換系數法，指出了熱電負荷優化分配的重大意義。

熱電負荷優化分配主要有等微增率法和遺傳算法等方法[5]。等微增率法的基本思路是首先分析機組的特點，得到一個特定的目標函數，然后確定機組總負荷和外特性約束，從而得到負荷分配的數學模型，利用數學優化方法求解最優解，從而解決汽輪發電機組并聯運行的經濟調度和負荷分配問題[6-7]。孫耘等人[8]針對等微增率法的局限性，提出了根據微增煤耗率分配各機組功率，提高了電廠的經濟效益。近些年已應用遺傳算法來求解負荷的經濟分配，它是一種流行和有效的算法，優化時將決策變量映射為某種進制鏈碼，依據進化論思想對決策變量進行全局尋優。柏春光等人[9]通過結合理論和實驗建立了機組的熱耗特性曲線，利用遺傳算法對熱電負荷進行了優化，實現了良好的節能效果。冉鵬等人[10]利用遺傳算法具有的非線性映射能力，驗證了遺傳算法實現優化分配的可行性。葉青等人[11]基于大數據及先驗知識獲取了實際耗差曲線，通過改進的遺傳算法實現了熱耗率的精確計算和熱電負荷動態分配。本文針對某具有多種機型和多抽汽點復雜情況的熱電聯產機組，提出一種改進的遺傳算法，解決了優化過程中的等式約束問題以及背壓機的熱負荷和電負荷的強耦合性對負荷優化分配帶來的困難；并針對遺傳算法中適應度函數的定義問題，提出了一種基于試驗數據的指數尺度變換系數改進方法，解決了常規遺傳算法易陷入局部優化的問題，實現快速準確的全局優化。實際優化結果表明，該方法極大的提高了背壓機在熱電負荷分配時的優化精度，可以實現在合理范圍內的對純凝機組與背壓機組聯合運行的熱電負荷分配計算，對提高機組運行經濟性具有一定的指導意義。

1 熱電聯產機組概況

某熱電廠現擁有6臺汽輪發電機組、7臺燃煤鍋爐，裝機總容量達到730 MW。分三期建設，一期裝機(#1、#2機組)2×125 MW凝汽式供熱機組，配備3×360 t/h燃煤鍋爐；二期裝機(#4機組)1×350 MW凝汽式供熱機組，配備1臺1 165 t/h燃煤鍋爐；三期裝機(#6、#7機組)2×40 MW+1×50 MW(#8機組)背壓機組，配備3×410 t/h燃煤鍋爐。

該電廠各機組之間的熱電負荷情況如圖1所示。各臺機組的功率、采暖抽汽、1.275 MPa工業抽汽以及2.8 MPa工業抽汽的上下限如表1所示。其中功率的單位為MW，抽汽量的單位為t/h。

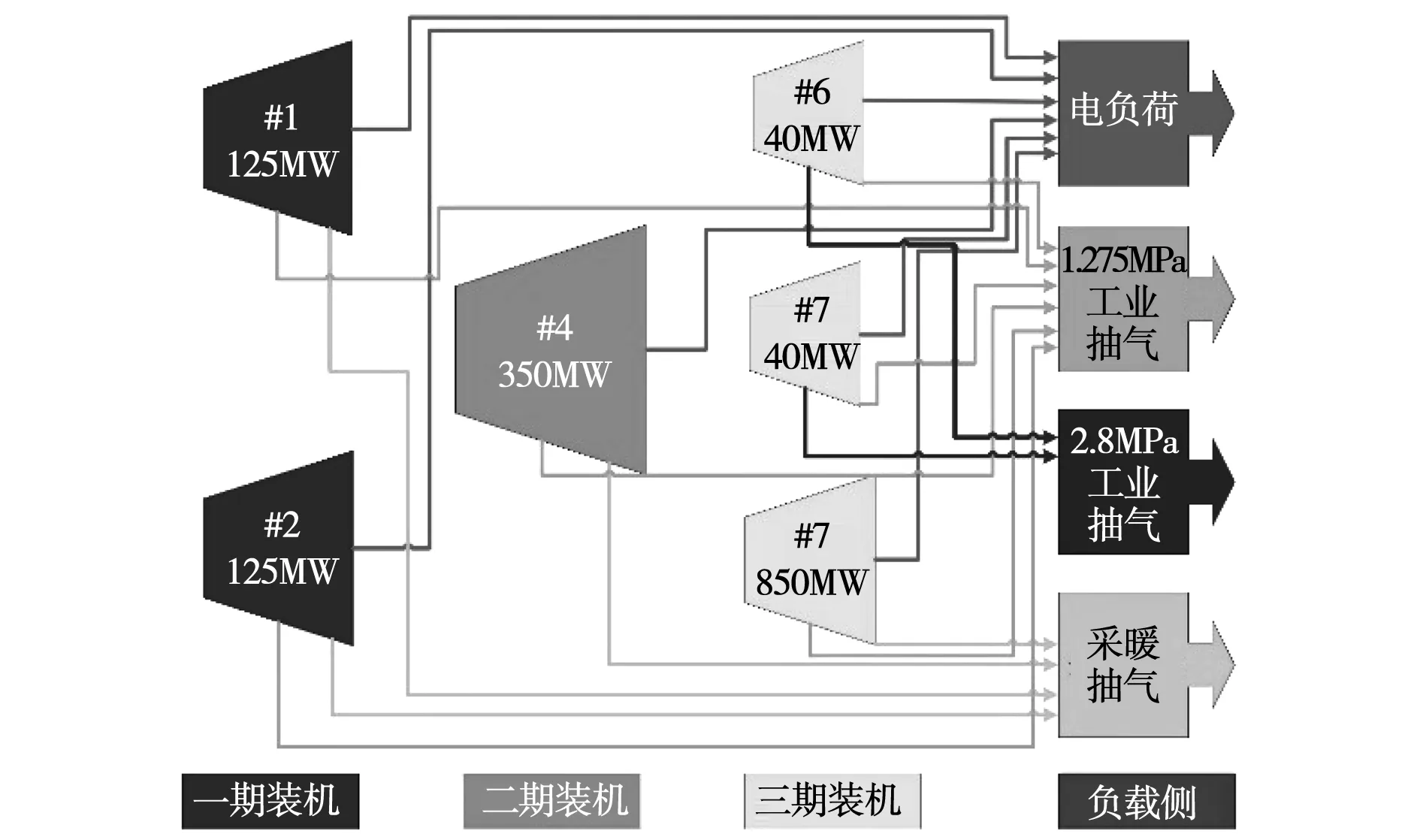
圖1 各機組熱電負荷連接圖

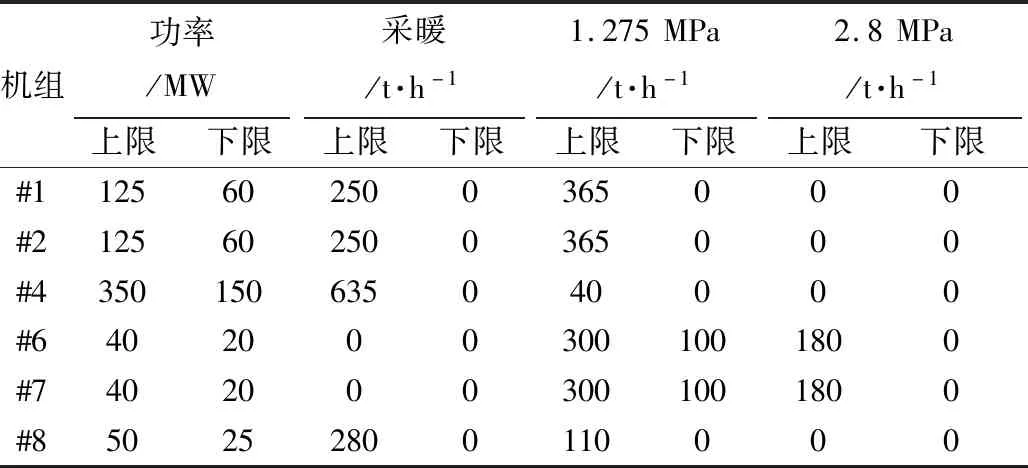
表1 各機組功率及抽汽量限值

某時刻6臺機組總發功率為495 MW、采暖抽汽量為1 106 t/h、1.275 MPa工業抽汽量為490 t/h和2.8 MPa工業抽汽量為100 t/h，該時刻運行要求下機組的運行功率、采暖抽汽量、工業抽汽量及熱耗情況如表2所示。其中功率的單位為MW，抽汽量的單位為t/h。

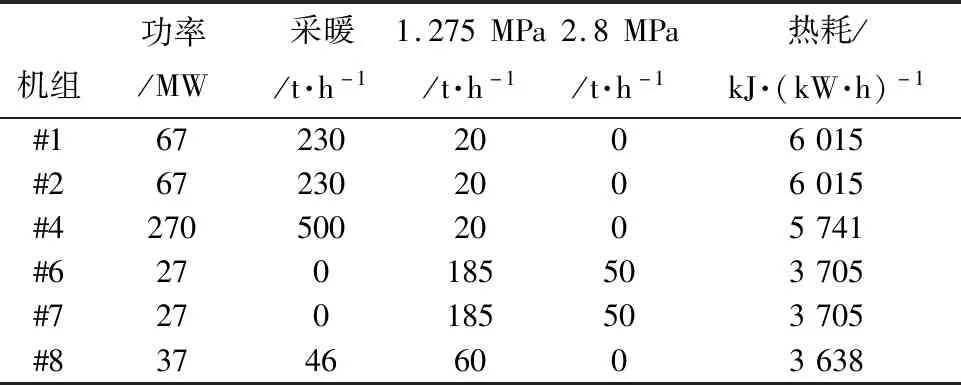
表2 該時刻各機組功率及抽汽情況

2 基于改進遺傳算法的熱電負荷優化分配方法

2.1 傳統遺傳算法

遺傳算法基于自然界中生物的進化過程，通過模擬生物演變進程搜尋最優解。該算法直接操作其結構對象，沒有函數可微的限制。從內部看，它具有隱并行性和較好的全局優化能力。并且其使用的是概率化尋優法，避免了規則的確定等步驟，可以自動建立搜尋空間，動態調整搜尋方向。在遺傳算法中，首先以一個群體的每一個個體為對象，然后利用隨機化方法指定一個編碼了的參數空間，最后進行快速高效地搜索。它的基本操作包括選擇、交叉和變異，其基本步驟如圖2所示。

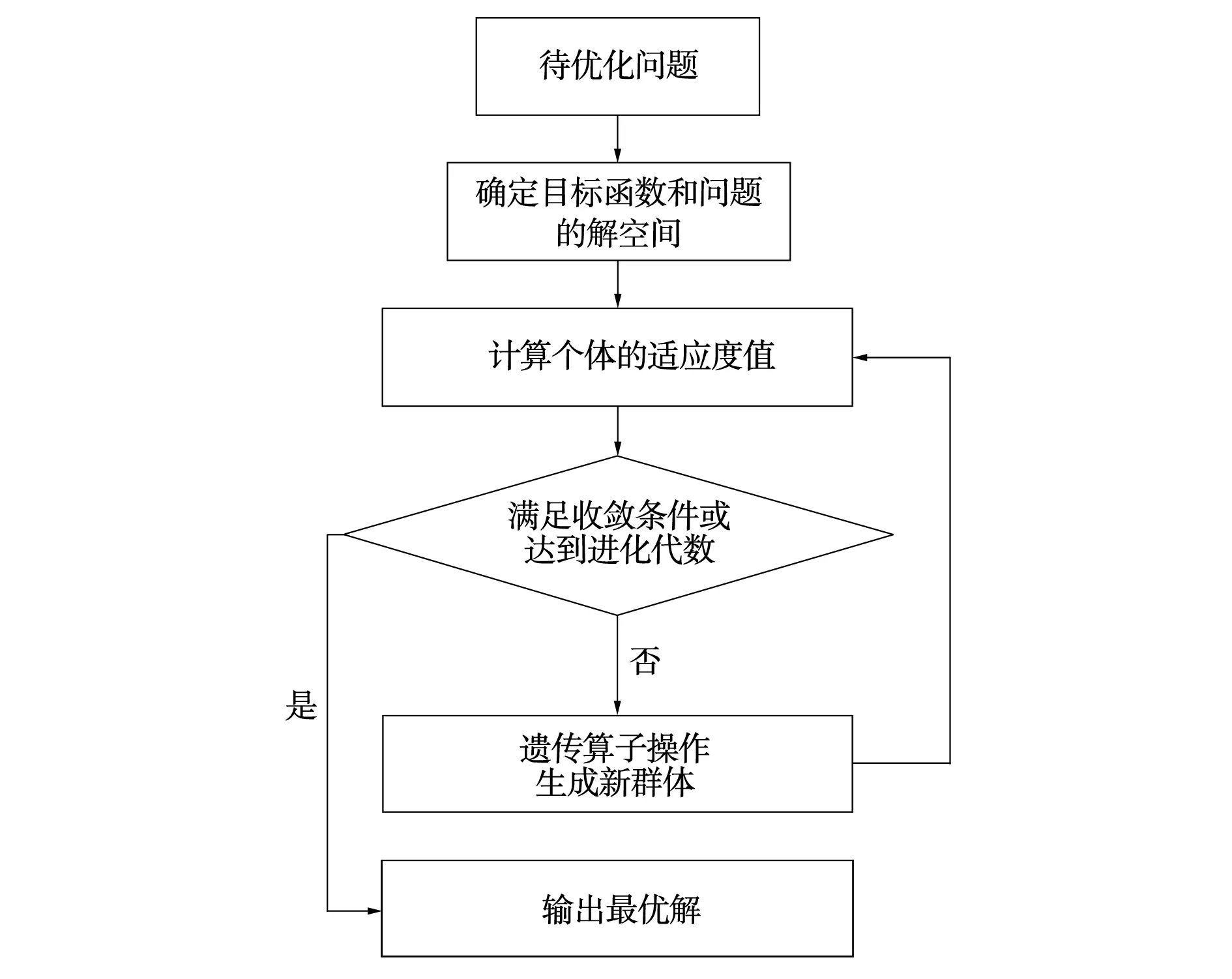
圖2 遺傳算法基本步驟

遺傳算法的首要問題是參數編碼，遺傳算子的運算方法直接受到編碼方式的影響，甚至在一定程度上還會影響進化的效率。目前，二進制編碼法、浮點編碼法、符號編碼法已經被廣泛采用。

然后，基因中的染色體代表算法的解決方案，并且提出用適應度函數來表征方案的好壞。因此，基因組和其適應度函數構成了一個映射。其中，適應度函數也代表了染色體和最優解染色體的距離。

類似于生物的進化過程，遺傳算法也按照“物競天擇，適者生存”的原則篩選算子，其中，適應度高的具有較大的概率傳至下一代，相反，適應度低的將被淘汰。

遺傳過程中，染色體隨機配對相互交換部分基因，產生新的基因型，形成新的個體，這個過程稱為交叉。個體的染色體中的某些基因若被其它的等位基因所替換而產生新個體則稱為變異。交叉體現了算法的全局尋優能力，變異體現了算法的局部尋優能力。二者結合將確保算法整體上的優化能力。

如前所述，遺傳、交叉、變異、自然篩選等基本操作將產生新一代的個體，對應著新的解，并通過自然選擇逐步淘汰了適應度低的解，保留了適應度高的解。如此循環下去，將有望找到適應度極高的解，該解即為遺傳算法所尋求的最優解。

2.2 多機組、多抽汽點情況下的優化問題

此前利用遺傳算法進行熱電負荷分配優化的研究大多局限于同一類機組且各臺機組只含有一段抽汽的情況。本文面向的是既含純凝機又含背壓機，且各機組存在兩段抽汽的問題。

因此，對于含有六臺機組的該電廠的熱電負荷分配優化研究，需要計算出給定熱負荷和電負荷下的每臺機組的功率、第一段抽汽量和第二段抽汽量，這導致所需優化的參數眾多、增加了算法的復雜程度和計算難度。該電廠中6臺機組的總電負荷、總采暖供熱量、總1.275 MPa工業抽汽量和總2.8 MPa工業抽汽量為給定的負荷條件，這四個值在遺傳算法中為等式約束條件，優化后的結果需滿足這些等式約束，而遺傳算法由于其隨機性，很難解決等式約束。對于含有四個等式約束的問題，不僅會降低遺傳算法的尋優速度，還可能使計算陷入局部最優解，從而降低熱電負荷分配優化的精度。

此外，整個調配系統中含有背壓機，其熱負荷和電負荷具有很強的耦合性，兩者間互相影響程度高。背壓機很難在電負荷不變的情況下，改變熱負荷，二者間存在相互制約，這也增加了遺傳算法尋優的難度。

2.3 改進的遺傳算法

通常情況下，進行熱電負荷分配計算的過程是采用遺傳算法對每臺機組進行電負荷、一段抽汽、二段抽汽負荷的尋優工作，目的是找到滿足總的負荷需求且總熱耗最小的運行狀態[12]。對于每臺機組的電負荷Q和其第一段抽汽P、第二段抽汽S，通過熱耗曲線取得相應的熱耗R，優化的目標如式(1)所示

(1)

這也是遺傳算法的適應度函數ObjV。需要將問題的可行解進行編碼，表達為遺傳空間的染色體或個體。針對該多維、高精度優化問題，將單個個體Q1Q2Q4Q6Q7Q8P1P2P4P6P7P8S1S2S4S6S7S8的18個基因值用相應地浮點數來表示，其編碼長度取決于決策變量的位數。

遺傳算法中個體在進行每次遺傳、交叉、變異時，根據實際過程中每臺機組的電負荷和抽汽量的上下限以及適應度值，對某一代個體給予適當的懲罰，從而確定最優個體。根據該電廠的實際情況，各機組的電、熱負荷存在上下限值，即：Qmax、Qmin、Pmax、Pmin和Smax、Smin，且6臺機組的總體電負荷和抽汽量為定值。

對于2.2節中提到的等式約束帶來的問題，本文的解決方法是：在使用遺傳算法時，只把其中5臺機組的電負荷和各段抽汽量進行編碼設置成染色體，而把剩下的一臺機組的電負荷和各段抽汽量通過式(2)計算，根據表1中各機組的各段抽汽情況，可得下式

(2)

式中Q——電功率;

B——1.275 MPa工業抽汽;

C——采暖抽汽;

D——2.8 MPa工業抽汽，下標為機組編號。如果得出如下結果

Q1Q1max,P1P1max

S1S1max,S6S6max

這一代的適應度值將受到極大的懲罰，從而影響接下來的遺傳、變異等操作。所以，經此改進后，每個含有18個基因的個體將變為只含有14個基因的個體，即：Q2Q4Q6Q7Q8P2P4P6P7P8S2S4S7S8。這不僅解決了等式約束帶來的問題，還減少了優化參數，有助于提高遺傳算法的尋優速度和精度。

對于2.2節中提到的背壓機的熱電負荷耦合嚴重的問題，本文基于汽輪機先驗知識和大量的運行數據，建立了背壓機排汽量與電負荷和級間第一段抽汽量的模型，如式(3)所示，即在背壓機的電負荷和級間第一段抽汽確定后，其排汽量也基本確定。

S=f(G,P)

(3)

由于，#6、#7、#8機組為背壓機，故S6、S7、S8可根據上式由其余兩個變量確定。所以經上一步優化后含有14個基因的個體將變為僅含有12個基因的個體，即：Q2Q4Q6Q7Q8P2P4P6P7P8S2S4。同樣，經此改進后，不僅減少了變量個數，還解決了背壓機電負荷和熱負荷的耦合問題。

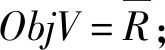
(4)

其中，a為常系數，當出現參數溢出上下界的情況時，予以極大的懲罰，使適應度值極小，相應的不合理染色體會以極大的概率被淘汰，從而保證產生的每一個參數的值都在用戶輸入的范圍內。

基于改進遺傳算法，可實現在合理范圍內的對純凝機組與背壓機組聯合運行的含兩段抽汽的調度系統進行熱電負荷分配計算。

3 熱電負荷優化分配結果

利用上述改進遺傳算法進行優化后，保持總功率和總各項抽汽量不變，各臺機組的優化后的功率、采暖抽汽量、1.275 MPa工業抽汽量、2.8 MPa工業抽汽量和熱耗如表3所示。可以看到，優化后的加權熱耗降為5211.48 kJ/(kW·h)，而優化前為5 435.92 kJ/(kW·h)，優化后煤耗降低了7.66 g/(kW·h)。十分明顯，經過優化后能明顯降低煤耗量。

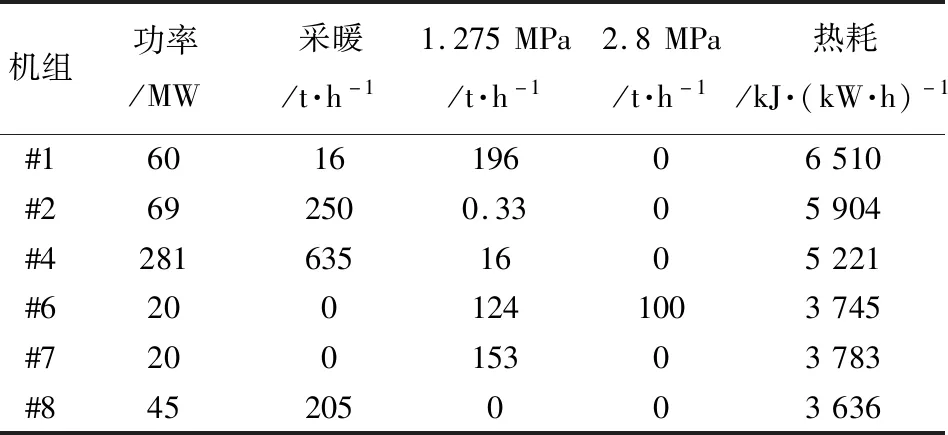
表3 優化后各機組功率、抽汽量和熱耗

4 結論

本文首先針對某電廠多機型、多抽汽點的熱電聯產機組之間的熱電負荷優化分配問題，提出了等式約束對遺傳算法計算效率和計算精度產生不良影響的解決方法。

然后，建立了背壓機排汽與功率和第一段抽汽量間的模型，解決了背壓機熱負荷和電負荷的強烈耦合對優化精度的影響。

鑒于通常情況下的遺傳算法在適應度函數選擇不當的情況下可能無法達到全局最優的問題，提出根據計算結果對適應度函數進行指數尺度變換，由此解決了常規遺傳算法容易局限于局部優化的問題，實現了快速而準確的全局優化。以上對遺傳算法的改進不僅減少了所需優化的參數的數目，還極大的提高了熱電負荷分配優化的精度，解決了算法容易陷入局部最優解的問題。

最后，實際運行結果表明，利用該方法對該電廠進行優化后的加權熱耗降低了224.44 kJ/(kW·h)，優化后煤耗降低了7.66 g/(kW·h)，可見該方法不僅可以解決多機型、多熱源的復雜機組間的熱電負荷優化分配問題，同時對熱電聯產機組的節能優化也具有一定的指導意義。