計及綜合需求側(cè)響應(yīng)的能源樞紐多目標運行優(yōu)化方法

黃旭銳，蘇亞納，侯宏娟,3，楊 波，潘 軍，朱以順

（1.廣東電網(wǎng)有限責任公司廣州供電局，廣東 廣州 510600；2.華北電力大學能源動力與機械工程學院，北京 102206；3.華北電力大學新能源電力系統(tǒng)國家重點實驗室，北京 102206）

綜合需求側(cè)響應(yīng)（integrated demand response，IDR）參與的能源樞紐系統(tǒng)在構(gòu)建綜合評價指標，因目標點可行域非凸，在確定權(quán)重方面存在難點。而目標的確定，是進行能源樞紐系統(tǒng)優(yōu)化的前提。

目前對于能源樞紐系統(tǒng)優(yōu)化的單目標模型中，通常在考慮IDR前提下從能效[1]或收益[2-3]方面進行優(yōu)化研究。但在多目標模型中，由于各個目標之間可能存在沖突，通常并不能得到使得每個指標都達到絕對最優(yōu)解。因此，更多的研究探索通過運用一些數(shù)學方法求得折衷解。文獻[4-5]采用模糊滿足技術(shù)選擇最佳折衷方案。文獻[6]將主觀與客觀賦權(quán)法結(jié)合，提出層次分析-熵權(quán)賦權(quán)法，從經(jīng)濟、能耗、環(huán)境3方面構(gòu)建評價指標。一些學者采用帕累托優(yōu)化方法處理多目標優(yōu)化問題：文獻[7]利用處理多目標凸優(yōu)化問題的標量化方法求解帕累托前沿（PF），將多目標優(yōu)化問題處理成凸優(yōu)化問題簡化了問題求解；此外，也有文獻利用智能算法進行多目標尋優(yōu)，采用遺傳算法[8-9]、粒子群優(yōu)化算法[10]、進化算法[11-12]等算法，優(yōu)化產(chǎn)生綜合能源系統(tǒng)最優(yōu)配置方案的帕累托前沿，通過決策者所考慮的目標價值、偏好等策略選擇合適的方案。但該類多目標能源樞紐優(yōu)化研究并未考慮到IDR參與的系統(tǒng)優(yōu)化問題。

對于未計及綜合需求側(cè)響應(yīng)的能源樞紐高效、經(jīng)濟等多目標運行優(yōu)化問題，可以通過分析權(quán)重確定綜合指標。而對于計及綜合需求側(cè)響應(yīng)的能源樞紐系統(tǒng)評價指標的建立方法，目前該類研究較少。因為綜合需求側(cè)響應(yīng)是通過預(yù)測需求側(cè)彈性負荷確定理想負荷分配/理想運行調(diào)度方案，進而調(diào)整價格引導用戶改變用能方式，但當以能耗、收益作為子目標時，計算模型非凸，也就是說博弈均衡后的能耗收益數(shù)據(jù)點在坐標系中的可行域非凸，進而難以確定多目標權(quán)重。

為了使計及綜合需求側(cè)響應(yīng)的能源樞紐系統(tǒng)供需博弈均衡點可行域為凸集，進而簡化多目標運行優(yōu)化方案的求解，本文采用“成本”替換“收益”作為子目標。由于成本只反映系統(tǒng)運行時的實際成本并不受供需博弈過程中價格的影響，從而可將供需博弈后的均衡點看成盡可能貼合能源樞紐理想負荷分配，將計及綜合需求側(cè)響應(yīng)的能源樞紐多目標運行優(yōu)化問題簡化為如何確定多目標需求下的理想負荷分配的問題。

綜上所述，本文對計及綜合需求側(cè)響應(yīng)的能源樞紐系統(tǒng)，基于日前多目標優(yōu)化問題，進行如下研究工作：1）建立能源樞紐各設(shè)備數(shù)學模型，以及分目標數(shù)學模型；2）建立綜合需求側(cè)響應(yīng)數(shù)學模型；3）基于用戶側(cè)負荷需求，通過標量化方法進行能源樞紐系統(tǒng)多目標權(quán)重分析并確定理想點，進而以目標向量點與理想點歸一化后的歐氏距離建立目標函數(shù)；4）以負荷分配為粒子，以在特定權(quán)重下能源樞紐運行的目標函數(shù)值為適應(yīng)度函數(shù)，通過粒子群優(yōu)化算法確定能源樞紐多目標需求下的理想負荷分配。

1 能源樞紐數(shù)學模型

能源樞紐基本架構(gòu)（圖1）包括蓄電、蓄冷、蓄熱設(shè)備，電熱泵（制熱），電熱泵（制冷），冷熱電聯(lián)供（combined cooling heating and power，CCHP）設(shè)備等能量轉(zhuǎn)化設(shè)備。能源樞紐一次側(cè)能源供應(yīng)包括電網(wǎng)、市政燃氣、風能和太陽能，二次側(cè)（需求側(cè)）包括電負荷、熱負荷和冷負荷3種類型。

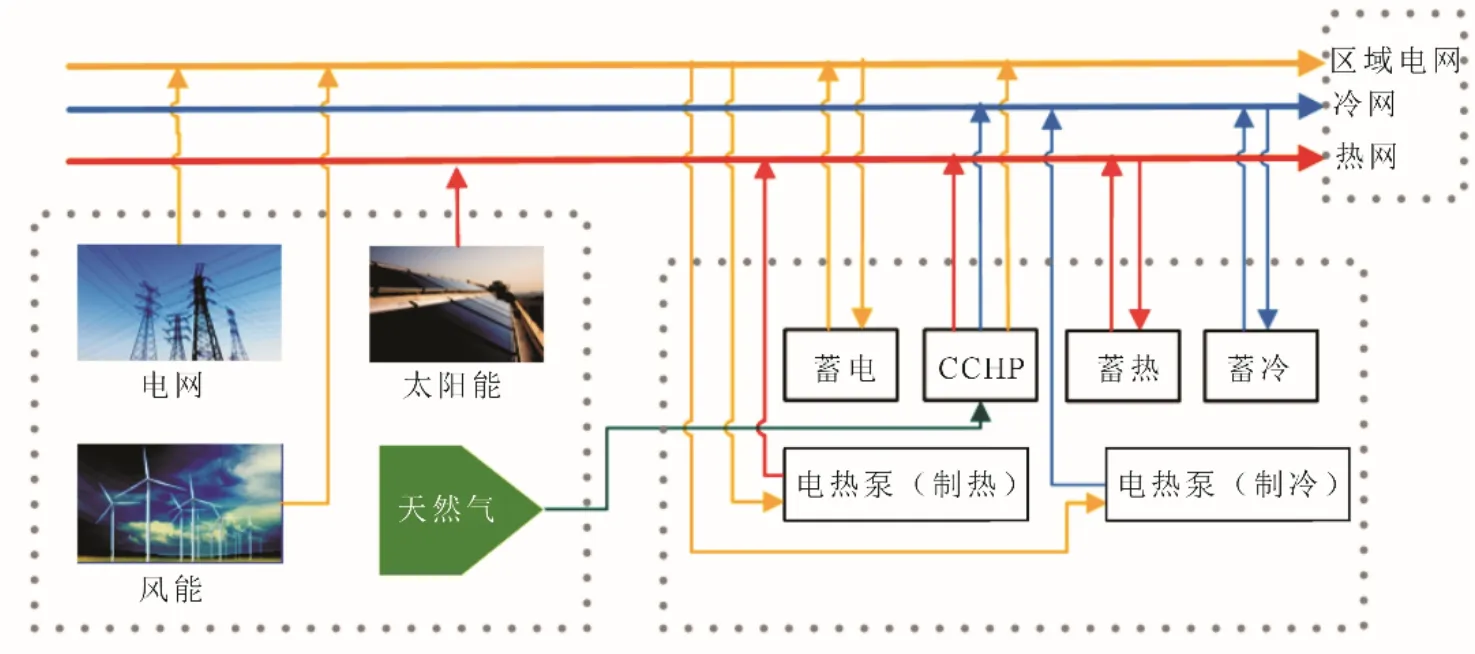
圖1 能源樞紐基本架構(gòu)Fig.1 Basic structure of the energy hub

1.1 冷熱電聯(lián)供系統(tǒng)約束

CCHP系統(tǒng)在最大出力和爬坡約束的前提下，還應(yīng)滿足在不同負荷率下的能量轉(zhuǎn)換關(guān)系：

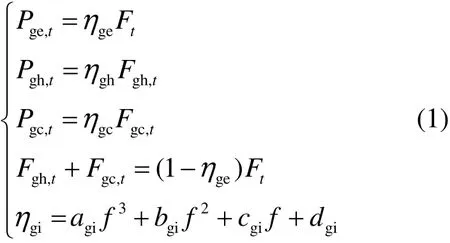
式中：t為時間節(jié)點；P為出力（其中冷/熱出力在計算上均以?來表示）；gi表示CCHP出力類型，gi即ge、gh、gc，分別代表CCHP供電、供熱、供冷；F為天然氣燃燒轉(zhuǎn)化的有用能；ηgi為CCHP的gi種出力的?效率；f為負荷率；agi、bgi、cgi、dgi為gi種用能方式中?效率與負荷率關(guān)系的相關(guān)方程系數(shù)。

1.2 儲能設(shè)備約束

儲能設(shè)備約束包括對電儲、熱儲、冷儲設(shè)備的充放約束、存儲狀態(tài)約束與調(diào)度周期的充放平衡約束，同時儲能設(shè)備應(yīng)考慮存儲容量與充放系數(shù)的關(guān)系。文獻[7]采用2個獨立變量表達儲能充放行為，并分析了系統(tǒng)在優(yōu)化過程中避免了儲能設(shè)備同時充放行為造成的額外能耗、成本、污染物排放量，所以本文將儲能的充放行為簡化為1個變量，其表達式為

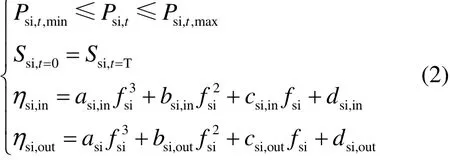
式中：Psi,t,min、Psi,t、Psi,t,max分別代表t時刻儲能設(shè)備si的充/放出力（正數(shù)為放，負數(shù)為充）以及出力的上下限；si（se、sh、sc）為儲能設(shè)備類型，分別代表蓄電、蓄熱、蓄冷；S為儲能設(shè)備?存儲量；ηsi,in、ηsi,out、fsi分別代表儲能設(shè)備si的充/放系數(shù)以及儲能設(shè)備存儲率；asi,in、bsi,in、csi,in、dsi,in、asi,out、bsi,out、csi,out、dsi,out代表儲能設(shè)備si的充放系數(shù)與設(shè)備存儲率關(guān)系的相關(guān)方程系數(shù)。

1.3 風電、光熱設(shè)備約束條件

鑒于系統(tǒng)存在棄風、棄光的可能性，對風電、光熱出力約束為

式中：下標w、s分別代表風電和光熱設(shè)備；Pt,max為t時刻天氣因素下的設(shè)備出力預(yù)測值

1.4 電制熱、電制冷設(shè)備約束

建立電制熱、電制冷設(shè)備線性數(shù)學模型，其約束為

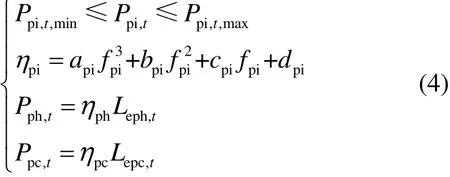
式中：下標pi=ph,pc分別代表電制熱、電制冷設(shè)備；ηpi、fpi分別代表pi設(shè)備能源轉(zhuǎn)化效率、負荷率；api、bpi、cpi、dpi代表pi設(shè)備能源轉(zhuǎn)化效率與負荷率關(guān)系的相關(guān)方程系數(shù)；Leph、Lepc分別代表電制熱、電制冷設(shè)備消耗的區(qū)域電網(wǎng)電量。

1.5 供需平衡約束

假設(shè)用戶側(cè)24 h負荷需求為L，t時刻負荷需求為Lt，t時刻的運行調(diào)度方案為Mt，表達式為

Mt需滿足的供需平衡方程如下：

式中：Pc代表市電購電量；下標egrid、hgrid、cgrid分別代表IES的電、熱、冷網(wǎng)。

1.6 子目標數(shù)學模型

1.6.1 能耗數(shù)學模型

單耗分析理論是基于?分析和?經(jīng)濟學分析的基礎(chǔ)上發(fā)展起來的能量系統(tǒng)分析方法[13-14]。本文基于單耗分析理論建立了系統(tǒng)能耗方程：

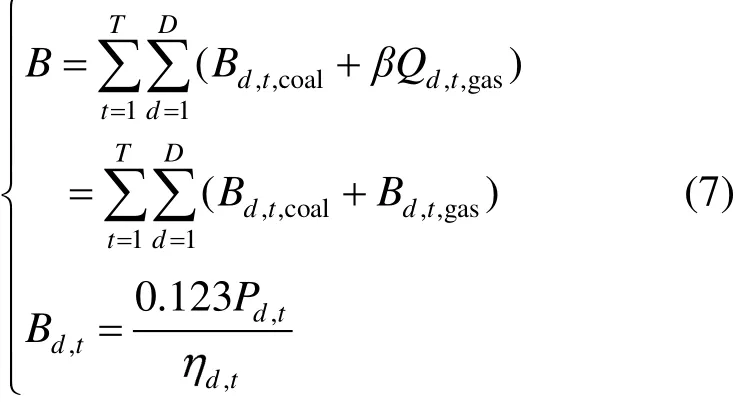
式中：B為總?cè)剂舷牧浚籺為時間，t=1,2,3,…,T，T為總時間；d為設(shè)備編碼，d=1,2,3,…,D，D為設(shè)備總數(shù)；Bd,t,coal、Qd,t,gas、Bd,t,gas分別表示t時設(shè)備d的煤耗（包括外網(wǎng)購電對應(yīng)的供電煤耗）、天然氣消耗量以及折算后的煤耗；β為天然氣-標準煤折算比，β=Cgas/Ccoal（其中Cgas、Ccoal分別為天然氣、標準煤的能值）；Pd,t為t時d設(shè)備出力；ηd,t為t時d設(shè)備的?效率。

1.6.2 成本數(shù)學模型

在IES的調(diào)度運行問題中，設(shè)備運行成本是成本目標函數(shù)的主要組成部分，主要包括IES的外電網(wǎng)購電成本、購氣成本以及系統(tǒng)運維成本。

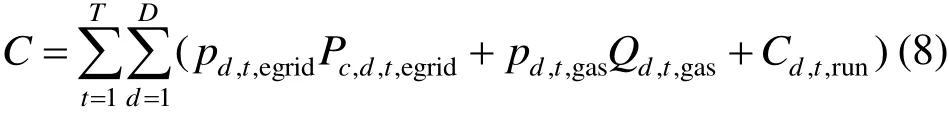
式中：C為運行調(diào)度總成本；pd,t,egrid為t時外電網(wǎng)購電價格；Pc,d,t,egrid為t時d設(shè)備市網(wǎng)購電量；pd,t,gas為t時天然氣購氣價格；Qd,t,gas為t時d設(shè)備天然氣購氣量；Cd,t,run為t時d設(shè)備運維成本。

2 綜合需求側(cè)響應(yīng)數(shù)學模型

在綜合需求側(cè)響應(yīng)中，多種負荷都有相應(yīng)的需求價格彈性。需求價格彈性表示各時段某類負荷對其價格的靈敏度，即在一定時段內(nèi)負荷變化率與該類負荷價格變化率之比：

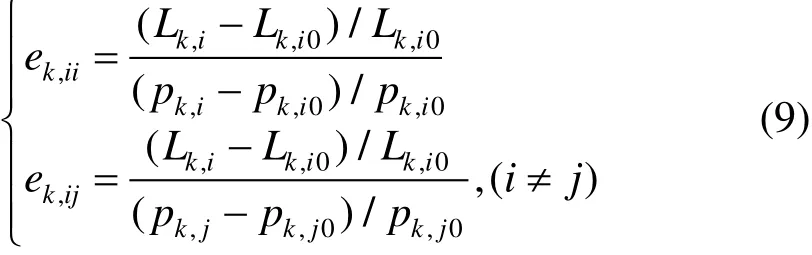
式中：ek,ii為i時段k類負荷用量隨該時段價格的變化情況，即該時段的自彈性；ek,ij為k類負荷i時段的負荷用量隨j時段價格的變化情況，即j對i時刻的交叉彈性；Lk,i0和pk,i0分別為i時段的k類負荷原始用量和原始價格；Lk,i和pk,i分別為實行分時價格后i時段的k類負荷用量和分時價格；

對于k類負荷而言，由自彈性和交叉彈性組成的彈性矩陣Ek為

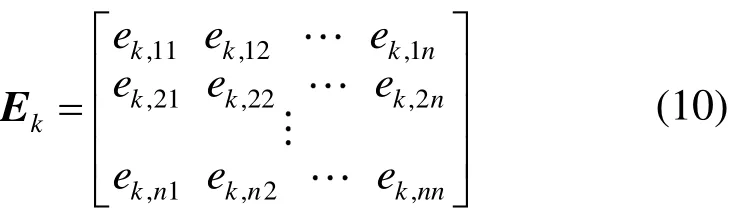
式中，n為時段數(shù)，如對于單日運行調(diào)度問題通常n取24。主對角線元素為自彈性，通常該值為負；非對角線元素為交叉彈性，通常該值為正。

3 能源樞紐運行優(yōu)化方法

3.1 多目標權(quán)重分析

能源樞紐通常以單日負荷需求，進行運行優(yōu)化。而對于單日多目標運行優(yōu)化問題，常采用標量化方法，遍歷權(quán)值求解帕累托前沿，最后通過某種策略進行最優(yōu)解選擇。

本文基于用戶側(cè)負荷需求，采用標量化方法過遍歷權(quán)值求取帕累托非劣解集合R，R∈帕累托前沿，表達式為

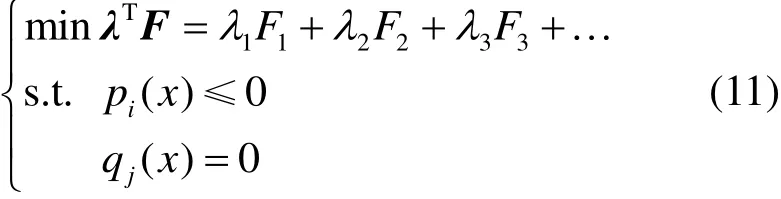
式中：λ為權(quán)向量；i為不等式約束條件編碼，i=1, 2,3, …；j為等式約束條件編碼，j=1, 2, 3, …。

采用理想點法，以目標向量點與理想點歸一化后的歐氏距離作為目標函數(shù)，表達式為

式中：M為n個小時運行調(diào)度方案，M=[M1,M2,M3, …,Mn]；N為目標個數(shù)；Fi、分別為第i個目標函數(shù)原始值、歸一化后的目標值；Fi,min為第i個目標最小值。通過公式(11)選取R中最優(yōu)解，進而確定多目標權(quán)重。

3.2 理想負荷分配求解

對于綜合需求側(cè)響應(yīng)參與下的能源樞紐系統(tǒng)而言，供需博弈行為意味著博弈平衡時的多目標在某種策略下優(yōu)于無綜合需求側(cè)響應(yīng)參與下的系統(tǒng)運行結(jié)果。而本文所建立的分目標在供需博弈過程中與博弈過程中的價格無直接數(shù)量關(guān)系，從而可將供需博弈后的均衡點看成盡可能貼合能源樞紐理想負荷分配，將計及綜合需求側(cè)響應(yīng)的能源樞紐多目標運行優(yōu)化問題簡化為如何確定多目標需求下的理想負荷分配的問題。

目前并無保證所求理想負荷配全局最優(yōu)的有效方法，為此本文采用一種局部最優(yōu)的優(yōu)化方法，即以負荷分配為粒子，以在3.1節(jié)特定權(quán)重下能源樞紐運行的目標函數(shù)為適應(yīng)度函數(shù)，通過粒子群優(yōu)化算法確定能源樞紐多目標需求下的理想負荷分配。

4 案例分析

以廣州夏至日某工業(yè)園區(qū)冷熱電負荷需求為例進行分析。日前，該工業(yè)園區(qū)24 h電、熱、冷負荷需求如圖2所示，其中，熱、冷負荷均是?負荷。由圖2可見：電負荷占最大比重，其主要用于工業(yè)生產(chǎn)與辦公；熱負荷主要用于園區(qū)的生活熱水和部分廠房生產(chǎn)用熱；冷負荷用于中央空調(diào)系統(tǒng)和部分廠房新風系統(tǒng)。夏至日均溫取31 ℃，熱網(wǎng)供水溫度55 ℃，冷網(wǎng)供水溫度7 ℃。假設(shè)各原始時刻電、熱、冷彈性負荷占比均為10%，均為可轉(zhuǎn)移負荷。

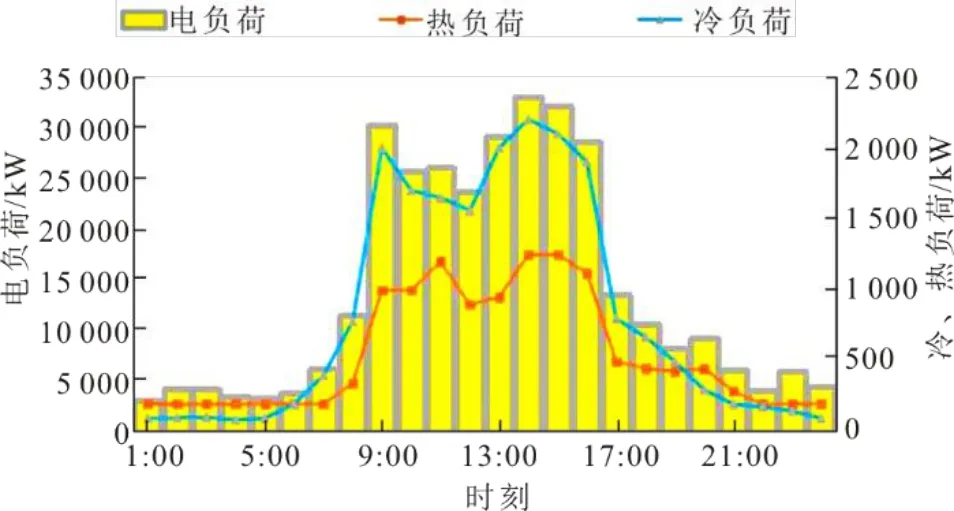
圖2 24 h電、熱、冷負荷Fig.2 The 24-hour electrical, heating and cooling load

以風電、光熱、CCHP、儲能設(shè)備搭建的能源樞紐系統(tǒng)為研究對象，分析在計及綜合需求側(cè)響應(yīng)參與下的能源樞紐系統(tǒng)日前多目標運行優(yōu)化調(diào)度方案。市電電價為0.5元/(kW·h)；天然氣熱值取35 564 kJ/m3，標準煤熱值取29 288 kJ/kg；1 m3天然氣相當于1.21 kg標準煤，天然氣價格取3.45元/m3；蓄電池最大容量為1 MW，蓄熱罐最大容量為0.3 MW，蓄冷罐最大容量為0.3 MW。電熱泵制熱時滿負荷能值系數(shù)取0.76，制冷時滿負荷能質(zhì)系數(shù)取0.61。各污染物排放系數(shù)取值參考文獻[15]。CCHP設(shè)備最大發(fā)電量取15.6 MW，最大制熱?量取2.23 MW，最大制冷?量取2.23 MW；電熱泵最大熱?出力取1.6 MW，最大冷?出力取1.2 MW；其他涉及到計算燃料消耗量的相關(guān)系數(shù)參照表1。

表1 案例相關(guān)系數(shù)Tab.1 Related coefficients of the case

4.1 不考慮綜合需求側(cè)響應(yīng)的能源樞紐系統(tǒng)多目標運行調(diào)度結(jié)果

基于圖2所示的原始負荷需求，根據(jù)3.1節(jié)計算不考慮綜合需求側(cè)響應(yīng)時的能源樞紐系統(tǒng)多目標運行調(diào)度結(jié)果。

其中標量化方法的步長取0.001。求解的雙目標問題的帕累托前沿如圖3所示。圖3中，紅色數(shù)據(jù)點為帕累托非劣解，藍色點(207 845, 441 123)為理想點，綠色點(212 021, 445 416)對應(yīng)的公式(11)目標函數(shù)值最小點，該綠色點所對應(yīng)的權(quán)向量為(0.205, 0.795)T。

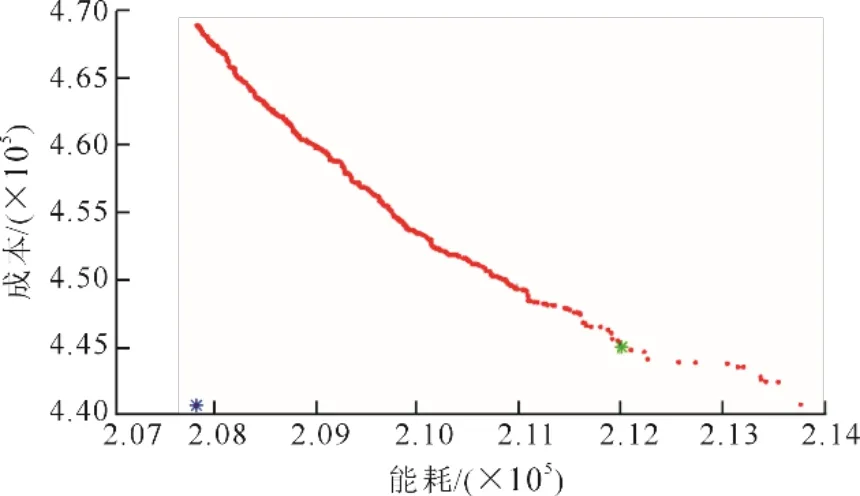
圖3 雙目標問題的帕累托前沿Fig.3 The Pareto fronts of two-objective problem

4.2 計及彈性負荷的能源樞紐系統(tǒng)多目標理想負荷分配

基于圖2所示的原始負荷需求，已知原始時刻電、熱、冷彈性負荷占比為10%。采用粒子群算法，以負荷分配為粒子（每一粒子各時刻運行方式均采用加權(quán)和單目標優(yōu)化方法，權(quán)向量為4.1節(jié)求得的(0.205, 0.795)T），以公式(11)所建立的目標函數(shù)為適應(yīng)度函數(shù)，其中粒子數(shù)為50，迭代周期為100。理想負荷分配及各時刻負荷調(diào)節(jié)量如圖4所示。

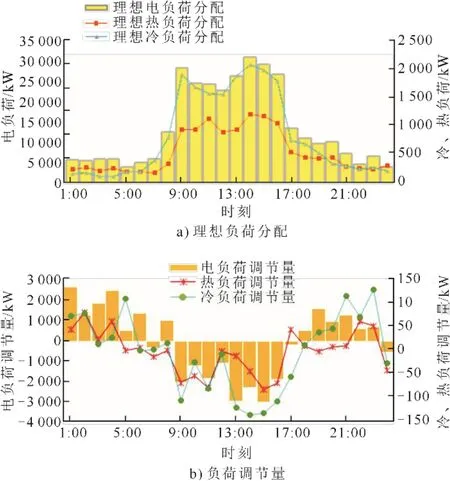
圖4 理想負荷分配及各時刻負荷調(diào)節(jié)量Fig.4 The ideal load-distribution and load regulations at each time

由圖4可以看出，理想負荷分配的峰谷趨勢相比于原負荷的峰谷更加平緩，這表明調(diào)整負荷分配有利于能源樞紐緩解高峰負荷需求，可以達到移峰平谷的作用。

另外，理想負荷分配對應(yīng)的運行調(diào)度能耗成本點為(210 412, 443 426)。對比4.1與該結(jié)果目標函數(shù)值，經(jīng)計算相比于4.1節(jié)的運行調(diào)度結(jié)果，該結(jié)果的目標函數(shù)值減小了39.9%。可見，在建立的多目標目標函數(shù)基礎(chǔ)上，調(diào)整負荷分配有利于能源樞紐對運行調(diào)度進行深度優(yōu)化。

4.3 計及綜合需求側(cè)響應(yīng)的能源樞紐系統(tǒng)供需博弈均衡時的運行調(diào)度結(jié)果

假設(shè)用戶側(cè)電、熱、冷負荷需求均由能源樞紐滿足，且用戶隨能源樞紐的價格波動，積極調(diào)節(jié)負荷需求。假設(shè)3種負荷初始價格均取0.5元/(kW·h)；交叉彈性數(shù)值均取1 000，自彈性數(shù)值均取0。供需博弈中，用戶側(cè)以最小用能費用為目標，以前次負荷需求向量為初值，在0.9~1.1倍初始負荷需求向量間通過非線性尋優(yōu)方法求解新的負荷需求向量；能源樞紐以盡可能貼近理想負荷分配為目標，同時考慮固定權(quán)向量下的結(jié)果有被支配解的可能，在一定范圍內(nèi)微調(diào)權(quán)向量；加入過往博弈記憶分析模塊，若當前博弈結(jié)果劣于前者，及時糾偏。實際負荷需求與理想負荷分配的偏差用D表示，表達式為

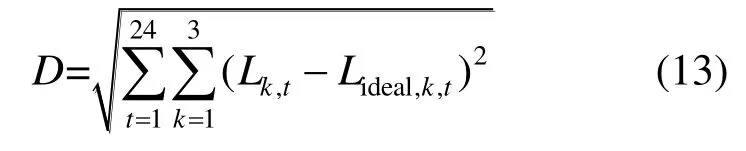
式中：Lk,t表示博弈過程中用戶側(cè)t時刻k類負荷需求量；Lideal,k,t表示理想負荷分配中t時刻k類負荷理想值。

計及綜合需求側(cè)響應(yīng)的能源樞紐與用戶側(cè)的供需博弈過程如圖5a)所示，紅色點為每一次博弈后的偏差D-用戶側(cè)用能成本點，隨著博弈次數(shù)的增加到50次之后出現(xiàn)了往復現(xiàn)象，最終均衡于藍色“*”點，即用戶側(cè)由初始負荷需求調(diào)整為均衡點時的負荷需求；圖5b)表示博弈過程中每次博弈的負荷分配所對應(yīng)的目標函數(shù)值。而圖6為博弈均衡時各負荷24 h價格。該價格相比于初始價格調(diào)節(jié)趨勢，與圖4理想負荷分配的各時刻負荷調(diào)節(jié)方向相反，以達到激勵用戶調(diào)節(jié)自身負荷需求貼近能源樞紐理想負荷分配的目的。

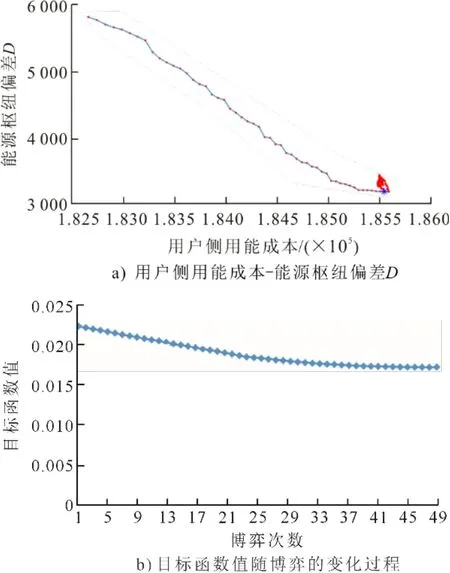
圖5 供需博弈過程Fig.5 The game progress of supply side and demand side

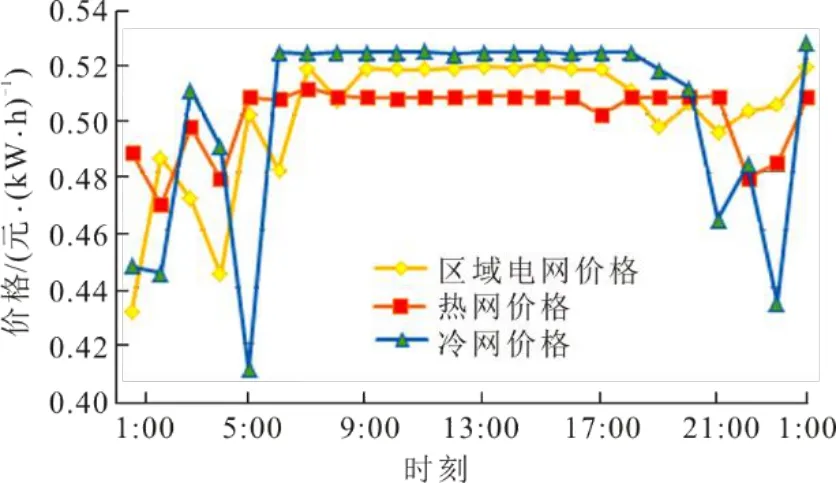
圖6 均衡點各負荷價格Fig.6 The price at each load at the balance point

另外，供需博弈均衡時的負荷分配所對應(yīng)的能源樞紐能耗-成本點為（210 133，446 935），相比于4.2節(jié)的運行調(diào)度結(jié)果，雖然該結(jié)果的目標函數(shù)值增加了16.8%，但相比于4.1節(jié)的運行調(diào)度結(jié)果，該結(jié)果的目標函數(shù)值減小了23.1%。

可見，基于綜合需求側(cè)響應(yīng)，能源樞紐應(yīng)用價格激勵措施引導用戶側(cè)改變用能方式。隨著供需博弈過程逐漸貼近理想負荷分配，優(yōu)化結(jié)果逐漸良好。即使達不到完全貼合理想負荷分配的要求，但貼近程度越高（偏差D越小），得到的優(yōu)化結(jié)果也越好。

5 結(jié) 論

本文基于計及綜合需求側(cè)響應(yīng)的能源樞紐日前多目標優(yōu)化問題，提出一種局部最優(yōu)的多目標優(yōu)化方法。建立了能耗、成本子目標函數(shù)，分2階段進行優(yōu)化：1）基于用戶側(cè)初始負荷需求，通過標量化方法進行能源樞紐系統(tǒng)多目標權(quán)重分析并確定理想點，進而以目標向量點與理想點歸一化后的歐氏距離建立目標函數(shù)；2）以負荷分配為粒子，以在特定權(quán)重下能源樞紐運行的目標函數(shù)值為適應(yīng)度函數(shù)，通過粒子群優(yōu)化算法確定能源樞紐多目標需求下的理想負荷分配。

通過實例驗證，計及綜合需求側(cè)響應(yīng)，合理地調(diào)整負荷分配能有效降低能源樞紐期望的目標函數(shù)值，而供需博弈過程中的負荷分配貼近理想負荷分配的程度越高，運行優(yōu)化結(jié)果越良好。