基于雙向耦合的綜合能源系統電熱聯合潮流計算

吳 瓊，吳彥琪，任洪波，王浩婷，謝 準

（上海電力大學能源與機械工程學院，上海 200090）

隨著經濟的快速發展，能源短缺以及環境污染等問題日益突出，能源互聯網[1]及綜合能源系統[2]等概念的提出為能源的清潔高效利用提供新思路。區域綜合能源系統中以熱電聯產機組（CHP）、冷熱電三聯產機組（CCHP）為耦合單元，實現了電氣熱多種異質能的耦合，大大提高了能源利用效率。隨著系統內多能源耦合趨勢逐漸加深，確定各個子系統的能量流分布，是能源互聯網和綜合能源系統領域研究的基礎，是探究多能互補特性、協同規劃、能量優化調度和協同管理等的重要前提，因此多能源耦合系統的多能流潮流研究具有重要意義[3-5]。

多能流潮流研究主要分為電氣網絡[6-8]、電熱網絡[9-11]以及電、氣、熱網絡[12-14]。在電、氣潮流研究方面，文獻[15]建立天然氣網潮流分析模型，將現有的天然氣水力計算方法與電力系統潮流計算方法相結合，提出了電氣混合潮流的順序求解法；文獻[16]提出了基于能源集線器理論的電氣網潮流計算方法，建立含有CHP的電氣網穩態模型，并考慮耦合節點作為平衡節點以及熱負荷變化對潮流計算的影響。在電、熱潮流研究方面，文獻[17]建立了計及回水管網熱損失的熱網遞推模型，對枝狀管網，提出了熱網潮流前推回代算法，然而熱網潮流前推回代算法不適于求解環狀管網；文獻[11]類比電網建立了環狀熱網潮流求解模型，提出了統一法和分解法求解電熱聯合潮流，然而并未考慮耦合單元耦合狀態；文獻[18]建立了基于改進能源集線器的電熱耦合網絡模型，求解電熱潮流，分析了綜合能源系統源-荷動態特性和生長型需求場景，然而熱網結構過于簡單。在電氣熱聯合分析方面；文獻[13,19]建立了電氣熱綜合能源系統穩態模型，采用統一法求解潮流，然而統一法對電、氣、熱網統一建模，不能充分利用現有電、氣、熱子網潮流計算成果，并且電氣熱網變量同時引入雅克比矩陣會大大增加矩陣的維度，使分析和編程復雜；文獻[20]提出了一種含有多種耦合單元的電、氣、熱潮流分布式計算方法，通過算例驗證分布式順序求解法在收斂速度優于統一法，但對不同耦合情況下不同運行方式順序求解流程過于復雜，難以推廣。

本文以熱電聯產區域綜合能源系統為研究對象。首先對環狀熱網，考慮熱網管道損失，建立了環狀熱網潮流模型；其次針對電熱耦合網絡中2個CHP耦合節點，建立了電熱雙向耦合潮流模型；然后考慮電鍋爐耦合狀態和電負荷變化，分析不同耦合模式和場景對電熱耦合潮流的影響；最后考慮系統源-荷變化，探究了電熱耦合網絡源-荷互動特性。為充分利用現有電熱子系統潮流計算成果，采用電熱順序求解算法求解電熱耦合潮流。

1 電熱綜合能源系統建模

含電熱耦合的綜合能源系統由電力系統、熱力系統以及CHP、電鍋爐、熱泵等多種耦合單元組成。電力系統主要由發電設備、電負荷以及輸電線路構成；熱力系統主要由熱源、熱負荷、供熱和回熱管網構成。電熱子系統節點分類及變量見表1。表1中：P、Q、V、δ分別為電力系統節點有功功率、無功功率、電壓幅值、電壓相角；Ts、Tr、Φ、m分別為熱力系統節點的供熱溫度、回熱溫度、熱源或熱負荷的熱功率、管道水流質量流量。

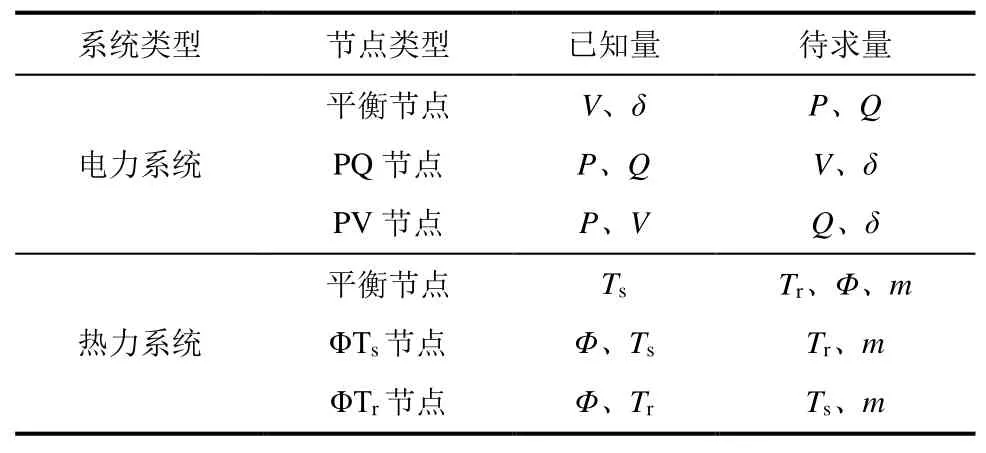
表1 電熱子系統節點分類及變量Tab.1 The node classification and variables of electric heating subsystem

1.1 熱力系統建模

在熱力系統中，熱網通常由供熱管網和回熱管網組成，以熱水或蒸汽的形式實現熱量由熱源到熱負荷的傳遞。含有1個熱源節點和2個熱負荷節點的簡單環狀熱網如圖1所示。熱水從熱源節點③經供熱管道1、2、3向熱負荷節點①和節點②供熱，同理熱水再經過回熱管道返回到熱源節點完成供熱循環。

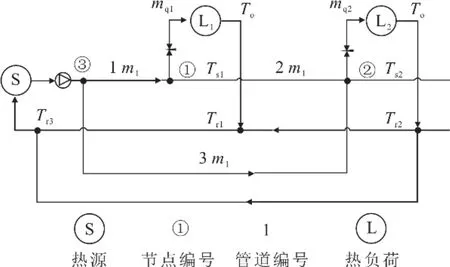
圖1 簡單環狀區域熱網Fig.1 The simple district heating network with a loop

熱力系統模型分為水力模型和熱力模型[11]。水力模型計算管道質量流量m，熱力模型計算熱負荷節點供熱溫度Ts、熱源和熱負荷節點回熱溫度Tr。通常情況下，熱源節點供應溫度和熱負荷節點出口溫度已知，除熱源平衡節點外，其他所有節點的熱功率也都是已知的。基于上述假設，建立了熱力系統模型。

1.1.1 水力模型

水力模型中的主要變量為管道質量流量m，且供熱管網和回熱管網相同，只需分析供熱管網即可。基于基爾霍夫第一定律和第二定律，考慮管網內質量流量的連續性和環狀回路中壓降為0，得出連續性方程和循環壓力方程為：

式中，A為節點-支路關聯矩陣，m為管道質量流量向量，mq為由熱負荷節點質量流量向量，B為回路—支路關聯矩陣，hf為由摩擦引起的管道壓頭損失向量。

A中元素Aij的取值為

B中元素Bij的取值為

對于每根管道，沿著管道的壓降和管道質量流量的關系為

式中，K為管道的阻力系數矩陣，用式(5)計算。

管道阻力系數與管道摩擦因數的關系為

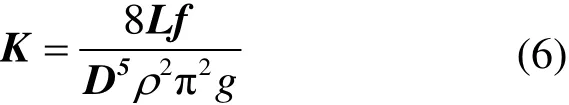
式中：L為管道長度向量；f為對應管道摩擦因數向量，詳細計算參考文獻[11]；D為對應管道直徑向量；ρ為水的密度；g為重力加速度。

1.1.2 熱力模型

在熱力模型中每個負荷節點有3種不同的溫度，即供熱溫度（Ts）、出口溫度（To）和回熱溫度（Tr）。通常，熱力模型中每個熱源節點的供應溫度和熱負荷節點的出口溫度已知，求解的變量為熱負荷節點供熱溫度（Ts）、熱源和熱負荷節點的回熱溫度（Tr）。基于能量平衡原理，得出熱力模型（包含熱功率方程、管道溫降方程和混合節點功率平衡方程）為：

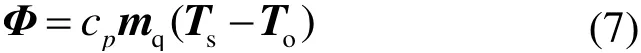
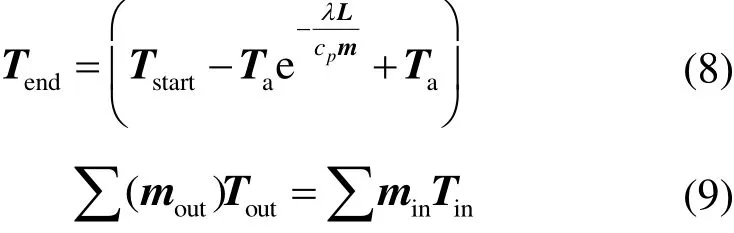
式中：Φ為熱負荷節點功率向量；cp為水的比熱容；Tstart、Tend分別為管道的開始節點、末尾節點的溫度，在供熱網絡中有Tstart=Ts，在回熱網絡中有Tstart=Tr；λ為單位管道長度的熱傳導系數；Ta為環境溫度；mout、Tout和min、Tin分別為流出和流入混合節點水流的質量流量、溫度。

1.2 電力系統建模

電力系統主要由發電設備、電負荷以及電網（輸電線路）構成。根據電力系統各節點已知量和待求量的不同，節點可分為平衡節點、PV節點、PQ節點。通過電力系統潮流分析，來確定電網中各節點有功功率、無功功率、電壓的幅值和相角。

通常，在電力系統潮流計算中，節點主要為PQ節點，即有功功率P和無功功率Q是已知的，節點電壓為待求量；由于節點電壓與功率之間非線性的關系，因此潮流方程也為非線性的。另外根據電力系統實際運行情況，須包含1個平衡節點，通過調節平衡節點的有功功率P來滿足系統的有功平衡；同時包含少量PV節點，通過在一定范圍調節無功功率Q來維持電壓幅值不變。

電壓的極坐標形式為

式中，z為虛部單位；δi為節點i的相角。

極坐標形式下的功率方程為：

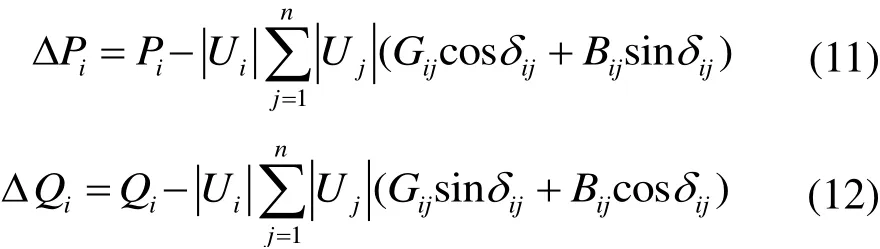
式中，Pi、Qi為注入節點i的有功功率和無功功率，|Ui|、|Uj|為節點i、j電壓的幅值，Gij、Bij為導納矩陣的實部與虛部，δij為i、j節點的相位差。

1.3 電熱耦合元件建模

電力系統和熱力系統通過電熱耦合元件（CHP、電鍋爐）等耦合。電鍋爐和CHP組合為1個具有可調熱電功率比的耦合單元，其熱功率和電功率輸出用引入的等效熱電比來描述。

1.3.1 熱電聯產單元

CHP作為電熱耦合的主要單元，供電的同時，通過余熱提供熱能，實現能量的梯級利用，有效地提高能源利用效率。

CHP的耦合模型為

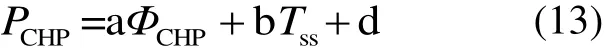
式中，PCHP、ΦCHP為CHP的電出力和熱出力，a、b、d為CHP常數。

在燃氣輪機和往復式內燃機的CHP中熱電比不變，為定熱電比機組；而抽氣式汽輪機組因冷凝模式不同使其熱電比變化，為變熱電比機組。

定熱電比機組中熱出力和電出力的關系為

變熱電比機組中產熱和產電的關系為

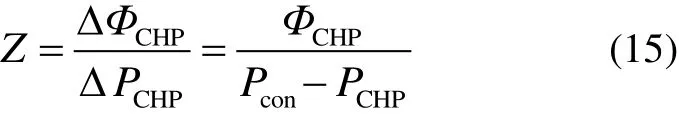
式中：ΔΦCHP、ΔPCHP分別為熱出力的增量和電出力的減少量；Pcon為全冷凝模式下CHP的電出力；Z為熱出力變化量和電出力轉換量的比率，Z可調。

1.3.2 電鍋爐

電鍋爐又叫電加熱鍋爐，是經過鍋爐將電力能源轉化成為熱能，向外輸出具有一定熱能的蒸汽、高溫水或有機熱載體的鍋爐設備。電鍋爐的數學模型為

式中，ηb為電鍋爐的效率，Φb為電鍋爐的熱出力，Pb為電鍋爐消耗的電功率。

電鍋爐和定熱電比CHP耦合的等效熱電比計算式為

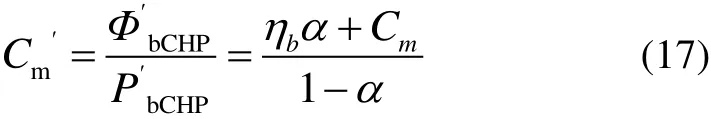
式中α為CHP電出力用于電鍋爐消耗電功率的比例。

2 電熱綜合能源系統潮流求解

針對電熱耦合綜合能源系統潮流模型的非線性特性，利用牛頓-拉夫遜法求解電熱綜合能源系統潮流。牛頓-拉夫遜法因其收斂性好、計算速度快成為最經典的潮流計算方法。

2.1 水力-熱力聯合潮流求解

基于牛頓-拉夫遜法，由水力模型和熱力模型導出熱力系統修正方程：

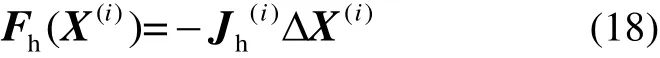
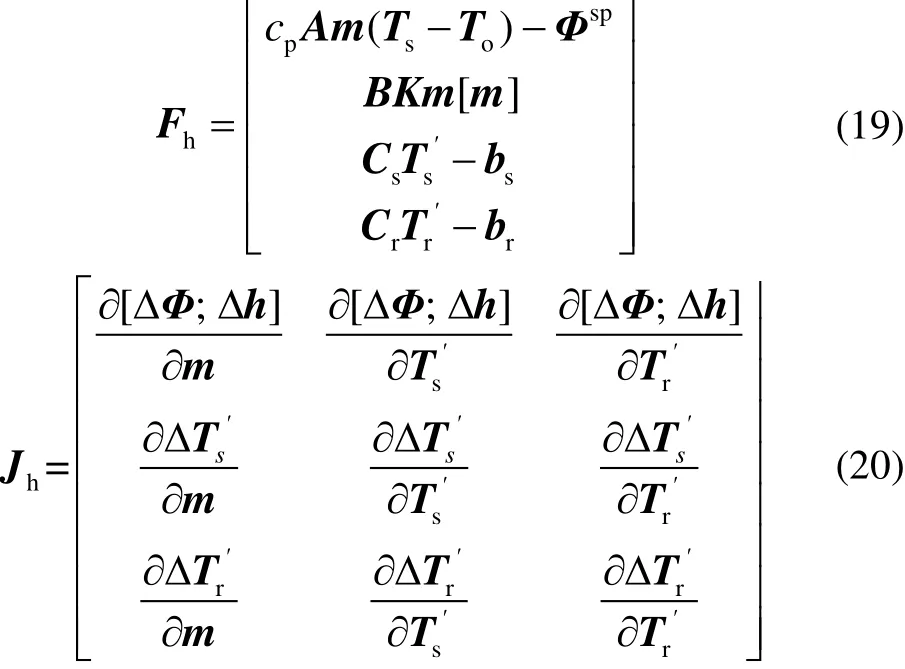
式中：i為迭代次數；Fh為熱力系統誤差向量；Jh為熱力系統雅克比矩陣；Φsp是給定的熱負荷向量；Ts′、Tr′為別為Ts、Tr和環境溫度Ta的差向量；Cs、bs和Cr、br分別為供熱網絡和回熱網絡的系數矩陣、解向量。

對熱力系統自變量m、Ts、Tr賦初值，通過修正方程反復迭代至滿足收斂條件，求解出熱力系統潮流分布。

2.2 電力系統潮流求解

基于牛頓-拉夫遜法，由電力系統潮流模型，導出電力系統修正方程，如下式所示：

式中：i為迭代次數；Fe為電力系統誤差向量；Je為電力系統雅克比矩陣；ΔP、ΔQ為有功功率和無功功率的偏差向量；Δδ、ΔU為電壓相角和幅值的偏差向量。

對電力系統自變量δ、U賦初值，通過修正方程反復迭代至滿足收斂條件，求解出電力系統潮流分布。

2.3 電熱耦合綜合能源系統潮流求解

在熱力系統和電力系統潮流求解算法的基礎上，為了避免統一法中雅克比矩陣維數過高、分析和編程復雜等問題，采用順序法求解綜合能源系統中電熱耦合潮流。

本文針對2個CHP耦合節點，利用電熱順序求解算法，同時考慮2個CHP耦合節點之間相互影響，求解電熱聯合潮流。含2個CHP耦合節點順序求解流程如圖2所示。圖2中，CHP1、CHP2分別為電、熱平衡節點。首先給CHP1熱出力賦初值，得出熱力系統潮流和熱平衡節點CHP2的熱出力，進而由式(14)求得CHP2的電出力；進一步求解電力系統潮流，得出CHP1的電出力和熱出力；通過CHP1的熱出力誤差，反復迭代直到滿足收斂精度，求解電熱聯合潮流。

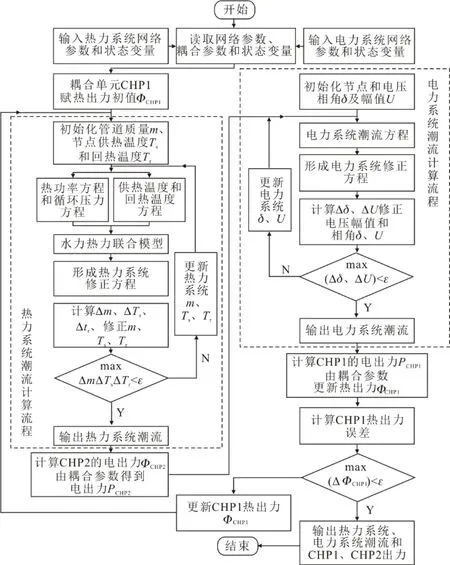
圖2 電熱雙向耦合潮流順序求解流程Fig.2 Flowchart for sequential solution of electric thermal two-way coupling power flow

3 算例分析

3.1 算例介紹

為了驗證所提模型的正確性，選取某一區域綜合能源系統電熱耦合網絡進行研究，其網絡拓撲如圖3所示。電力系統為IEEE標準14節點系統，其中發電機節點1、3用CHP代替，CHP1為變熱電比的機組，CHP2為定熱電比的機組；熱力系統采用17節點系統，管網參數見表2，假定熱源供熱溫度Ts=70 ℃，出口溫度To=30 ℃。

通過耦合單元CHP1（Pcon=0.85，Z=3）將電網節點e1和熱網節點h1耦合；通過耦合節點CHP2（Cm=1.3）將電網節點e3和熱網節點h17耦合；其中CHP1作為電平衡節點，CHP2作為熱平衡節點。同時為了調節電熱產出比例，在e3和h17之間耦合了電鍋爐（額定熱功率0.1 MW，ηb=98%），電鍋爐由CHP2提供電功率。

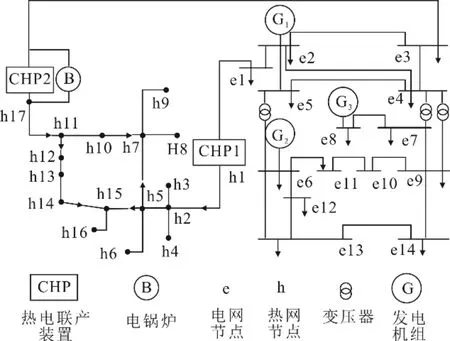
圖3 區域綜合能源系統網絡拓撲Fig.3 The network topology of integrated energy system

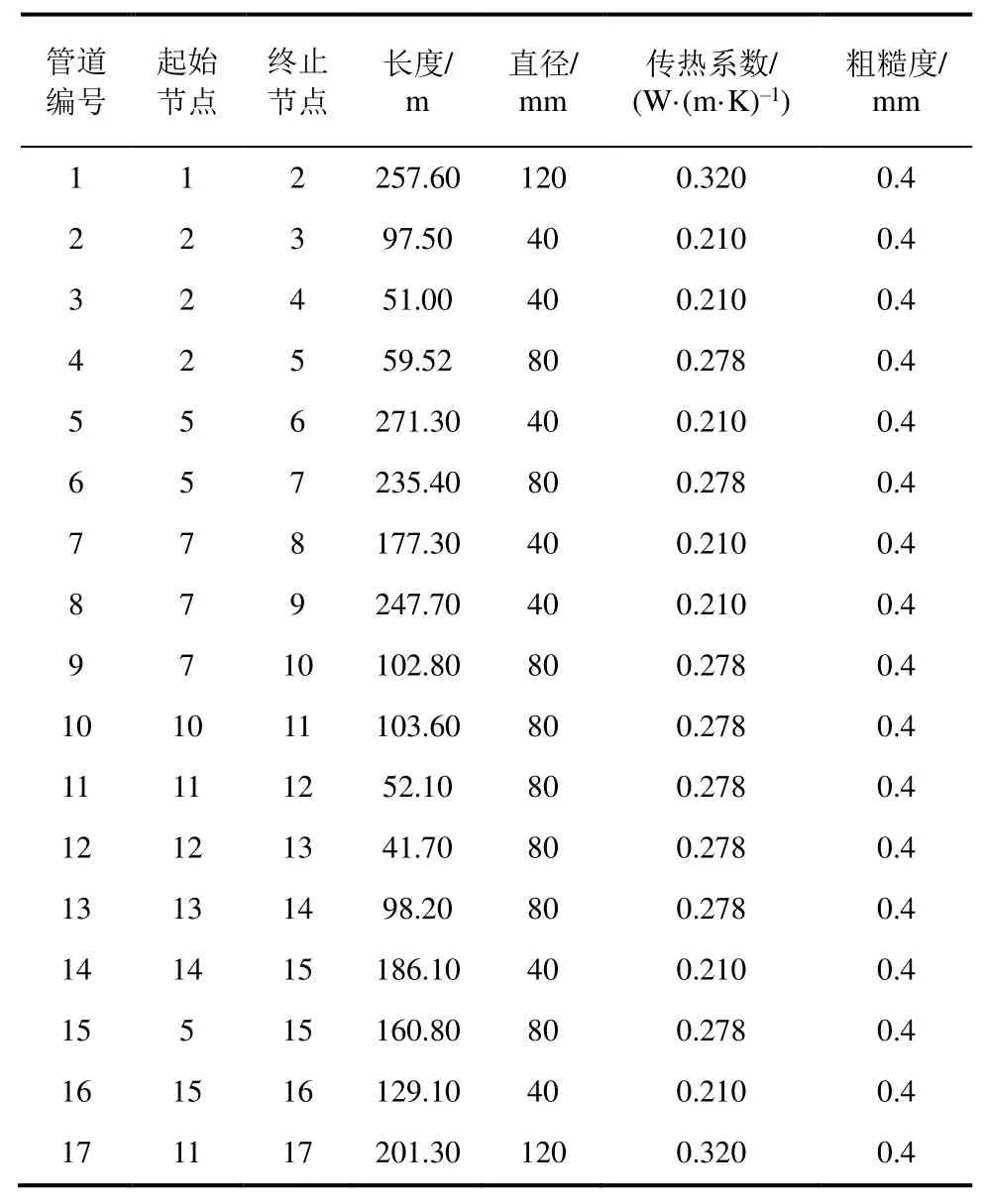
表2 熱力系統管網參數Tab.2 The parameters of thermal pipe network

考慮電鍋爐2種耦合狀態，耦合狀態1取α=0，耦合狀態2取α=10%；考慮電力系統電負荷變化的不同場景，場景1為初始電負荷，場景2為電負荷增加10%。針對電鍋爐2種耦合狀態和電力系統中電負荷變化前后2種場景，得出4種組合：1）模式1場景1下，電鍋爐與CHP2解耦，電負荷不變；2）模式1場景2下，電鍋爐與CHP2解耦，電負荷增加10%；3）模式2場景1下電鍋爐與CHP2耦合，電負荷不變；4）模式2場景2下電鍋爐與CHP2耦合，電負荷增加10%。

3.2 結果分析

通過上文的電熱耦合順序求解算法，基于MATLAB軟件2016b版本下編程求解出不同耦合模式不同場景下系統電熱潮流分布。表3為不同組合下熱力系統管道質量流量。由于CHP1和CHP2熱出力的相互影響，主流管道如管道1、4、6、9、10、17質量流量變化較大；尤其電鍋爐耦合狀態和電負荷同時變化時，17管道質量流量較大，需要足夠的壓差來維持可能導致壓力調節失控，在運行時應注意避免以及后續系統規劃中合理選擇管道參數和調壓設備。而且模式1場景2、模式2場景1、模式2場景2下6號管道水流方向與假設方向相反此時熱源CHP1和CHP2在節點5和節點15交匯。

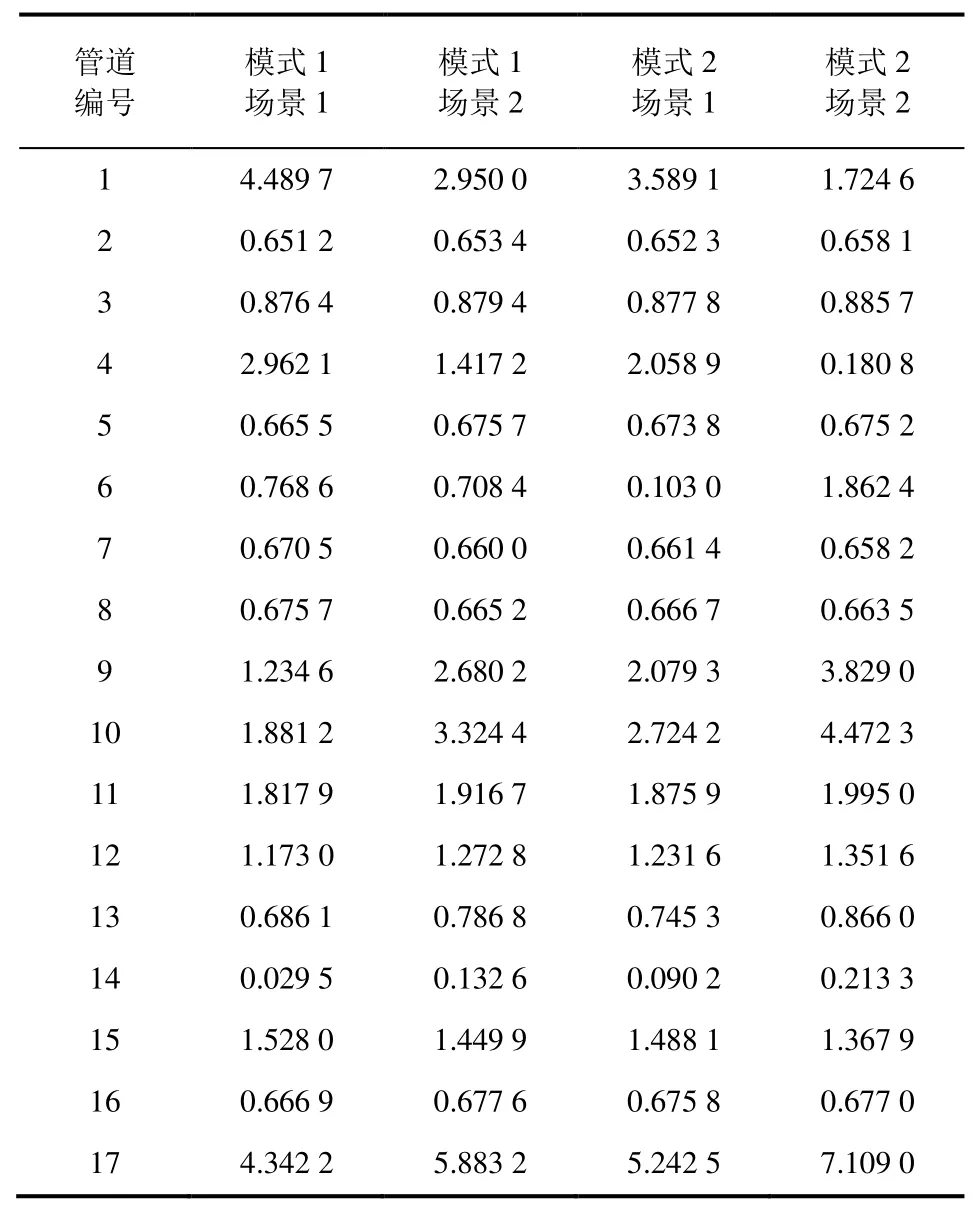
表3 熱力系統各管道質量流量 單位：kg/sTab.3 The mass flow of each pipeline in thermal system

表4 為不同組合下熱力系統節點的供熱溫度和回熱溫度。在供熱溫度中，模式1場景1的節點9為末端供熱節點溫度最低為67.864 1 ℃；而另外3種情況下節點6和16為末端供熱節點，溫度都較低分別為67.866 3、67.969 8、67.891 6 ℃和67.760 8、67.859 3、67.792 1 ℃；同時對于管道6關聯的節點5和7，不同組合下熱源交匯節點溫度均低于非交匯節點，主要是因為CHP1熱出力減少和CHP2熱出力增加。

圖4 為不同模式不同場景下電力系統電壓幅值的變化情況。模式1場景1和模式2場景1電壓幅值范圍為1.013 7~1.060 0，模式1場景2和模式2場景2電壓幅值變化范圍為1.008 6~1.060 0。不同情況下節點14的電壓均為最低，主要是因為遠離電源節點，且電負荷增加10%，電壓降落為0.005 1。電鍋爐在不同耦合狀態下，當電負荷相同時，電壓幅值基本保持不變，而電鍋爐在相同耦合狀態下，當電負荷變化時，PQ節點電壓幅值隨之變化。表明在該系統中電負荷對電壓幅值影響較大，而電鍋爐耦合狀態對電壓幅值影響較小，主要原因是電鍋爐耦合狀態變化時只影響耦合節點CHP1和CHP2的注入功率，總的注入功率未變，其他條件均未變。

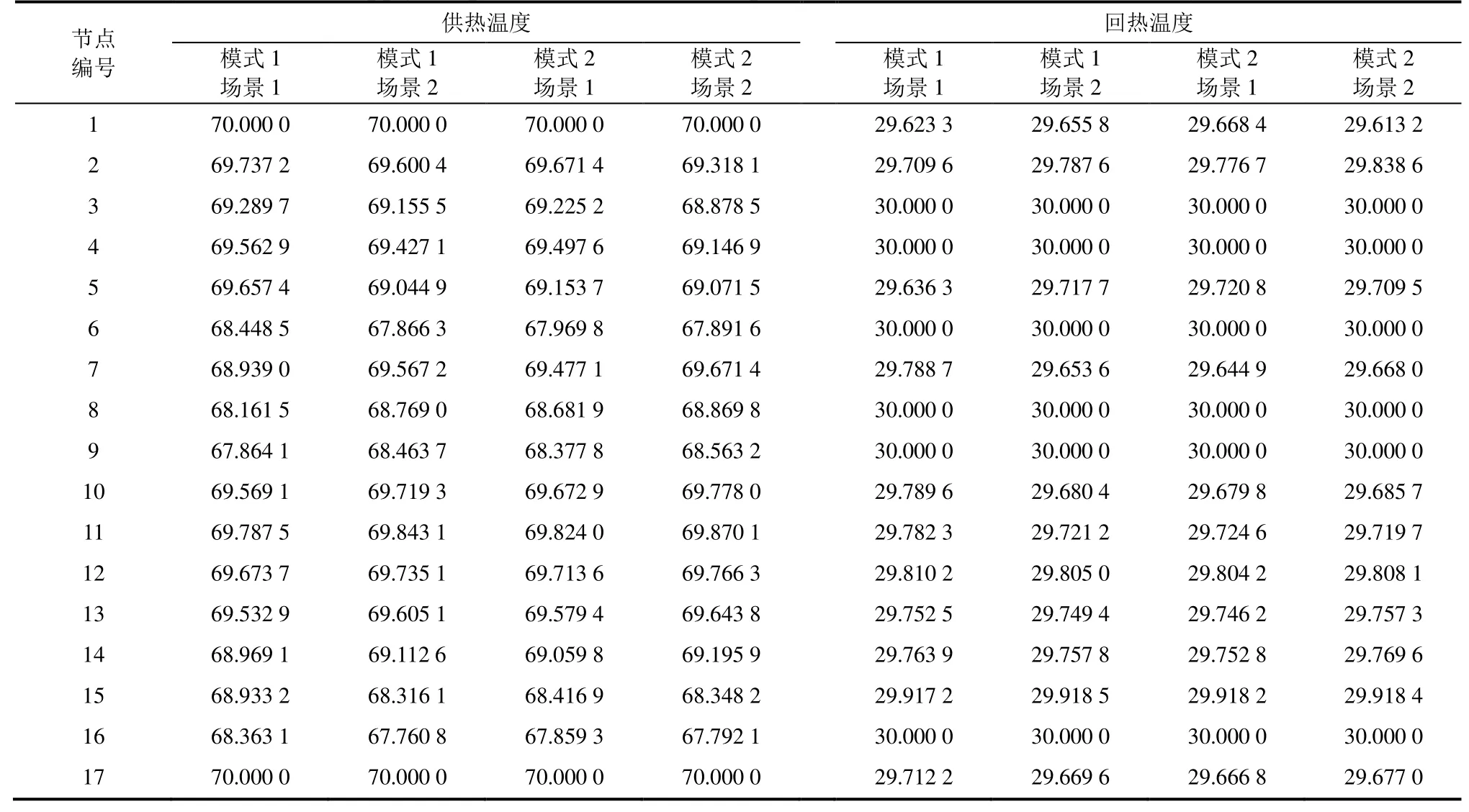
表4 熱力系統各節點供熱溫度和回熱溫度 單位：℃Tab.4 The supply temperature and return temperature of each node of the thermal system

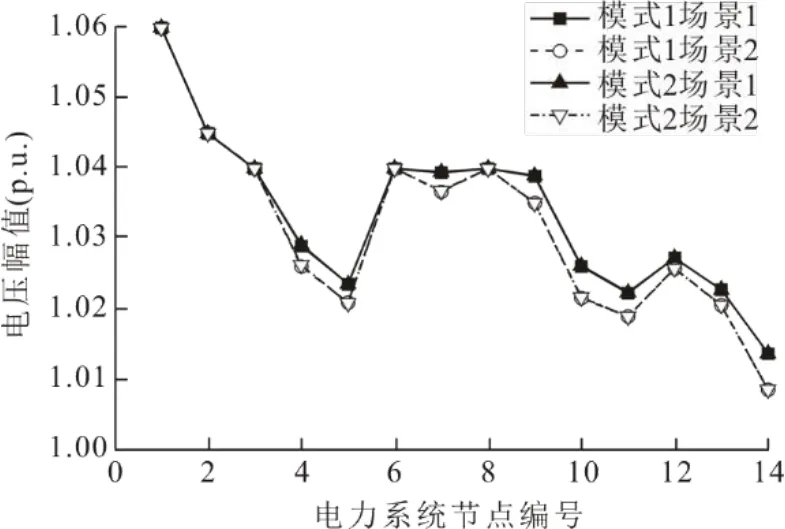
圖4 電力系統各節點電壓幅值Fig.4 The voltage amplitudes of each node in power system

圖5 和圖6分別為不同模式不同場景下熱力系統熱平衡和電力系統電平衡。

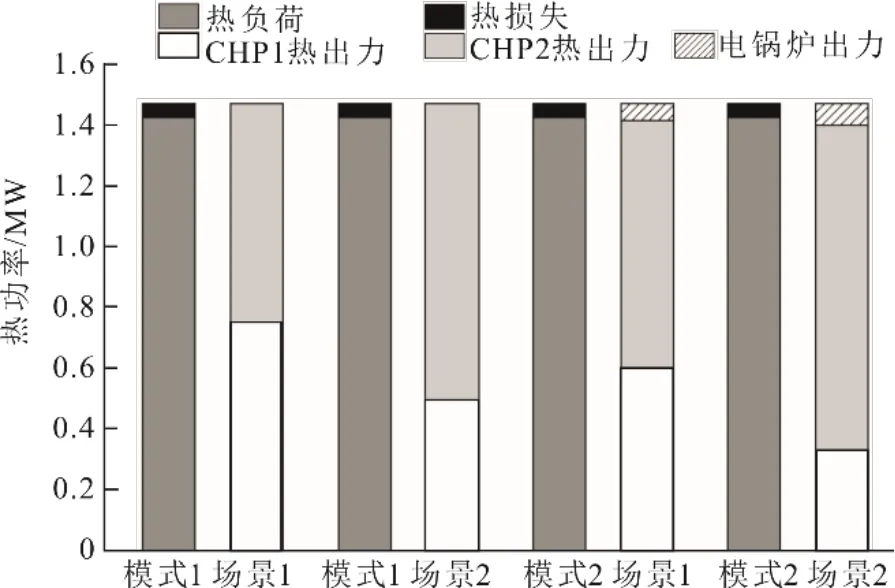
圖5 熱力系統熱平衡Fig.5 Heat balance of the thermal system

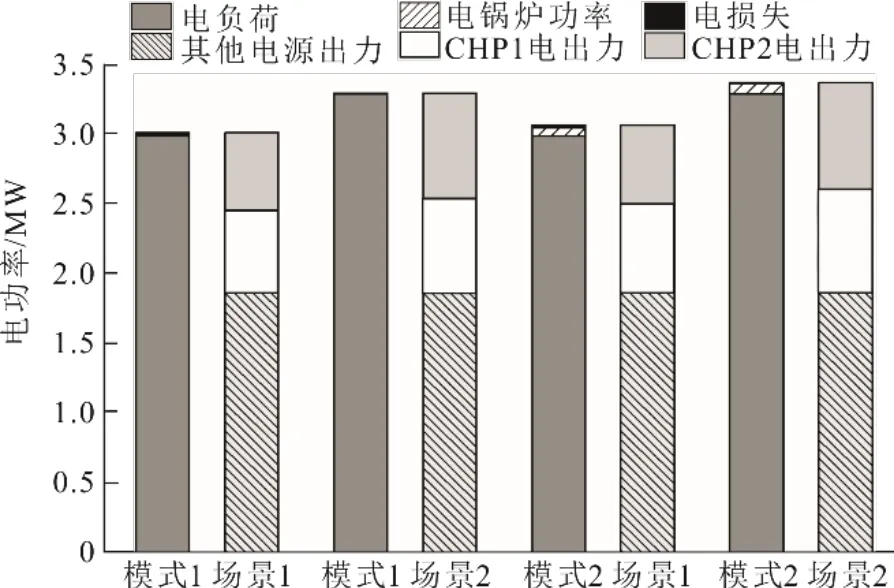
圖6 電力系統電平衡Fig.6 Electric balance of the power system

在電負荷不變時，電鍋爐接入耦合，增加了CHP2的電出力和熱出力，而系統的熱負荷不變，因此CHP1的熱出力減少；在電鍋爐耦合狀態不變時，電負荷增加10%，CHP1和CHP2電出力都增加，由式(14)和式(15)知CHP2熱出力增加，CHP1熱出力減少。綜上，模式2場景2下CHP1熱出力最少為0.291 3 MW，電出力最多為0.752 9 MW，CHP2熱出力最多為1.198 8 MW，電出力最多為0.771 8 MW。

3.3 雙向耦合特性及源荷互動特性分析

在綜合能源系統中，由于多種能源間存在耦合互動，源-網-荷任何狀態變化都會引起系統狀態改變。

3.3.1 雙向耦合特性分析

由圖2、圖5和圖6可知：在模式1場景1和模式2場景1下，系統負荷不變時，電鍋爐耦合狀態改變，首先引起CHP2熱出力和電出力的變化，進而通過電網引起電力系統潮流變化；然后影響CHP1的電出力和熱出力的變化，接著通過熱網影響熱力系統潮流的變化，反作用于CHP2；最終達到系統中CHP1、CHP2出力和潮流平衡。同理對模式1場景2和模式2場景2分析相同。

3.3.2 源-荷互動特性分析

在電熱耦合綜合能源系統中，由圖2知電熱子網的狀態變化會通過耦合單元傳遞給耦合子網，同時通過耦合單元反饋影響原子網，在耦合單元的雙向作用下，引起電熱子系統雙向交互。

圖7 為其他電源出力、電負荷、熱負荷變化時對熱力系統供熱溫度的影響。初始場景為模式1場景1，電負荷增加10%對應模式1場景2。當熱負荷增加10%時，溫度變化趨勢與初始場景相同，且負荷供熱溫度比初始場景均有所提高；當電負荷和熱負荷都增加10%時，溫度變化趨勢同電負荷增加10%時相同，且負荷供熱溫度比負荷增加10%時均有所提高；當其他電源出力、電、熱負荷都增加10%時，溫度變化趨勢與初始場景和熱負荷增加10%基本一致，主要原因是其他電源增加出力抵消了熱負荷的增加；但在節點14和15出現較大波動，主要是交匯節點由15變為14。

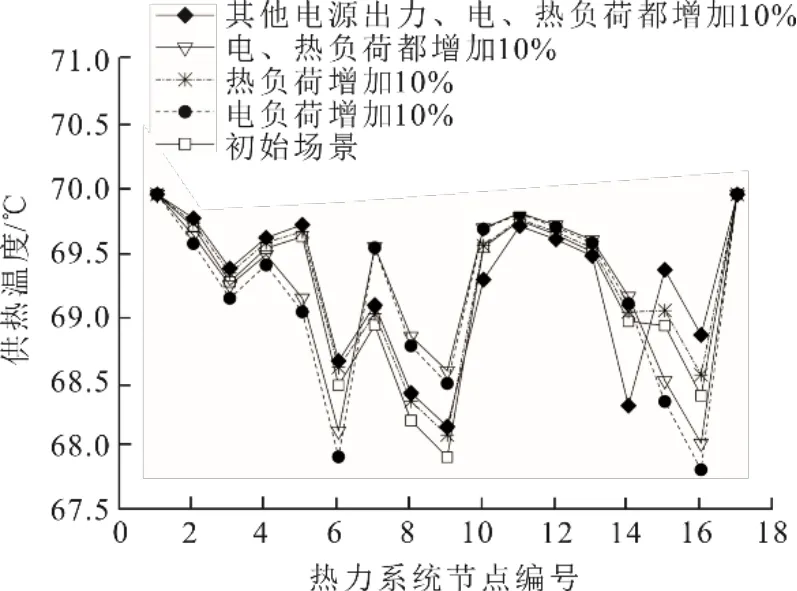
圖7 電源和電熱負荷變化對熱力系統的影響Fig.7 Influence of power supply and electric heating load change on the thermal system

圖8 為其他電源出力、電負荷、熱負荷變化時對電力系統電壓幅值的影響。初始場景和熱負荷出力增加10%以及其他電源出力、電、熱負荷都增加10%時的電壓幅值變化趨勢基本一致，主要是電源出力增加抵消了電負荷增加且熱負荷變化對電力系統電壓幅值影響較小。因此電負荷增加10%和電、熱負荷都增加10%，電壓幅值基本保持不變。

圖8 電源和電熱負荷變化對電力系統的影響Fig.8 Influence of power supply and electric heating load change on the power system

4 結 論

本文對含有2個CHP耦合節點的電熱雙向耦合潮流計算問題進行了研究，建立了電熱雙向耦合順序求解模型，通過算例驗證了該模型的有效性。為探究電熱雙向耦合特性和源-荷互動特性，進行了敏感性分析，得到以下結論。

1）系統在雙向耦合下，CHP1和CHP2通過電熱耦合網絡相互作用，CHP2節點耦合狀態的變化，引起CHP1狀態變化，同時反作用CHP2,使耦合單元出力和系統潮流重新平衡。

2）源-荷互動特性方面，電熱單個子網源-荷的變化，通過耦合單元引起耦合子網的狀態變化進而引起系統潮流的變化。由于電網中有獨立電源，熱網狀態變化對電網潮流影響較小，且電源側出力增加或減少會相應抵消電負荷增加或減少對電網潮流的影響。

3）需要指出的是，電熱耦合系統中源-網-荷任何一側狀態改變可能對系統狀態產生不利影響。通過模擬極端負荷或耦合單元故障等不利條件，發現電、熱網薄弱環節，為系統運行規劃提供數據基礎。