Controllable four-wave mixing based on quantum dot-cavity coupling system

Hong-Wu Xing,Bin Chen,2,*Li-Li Xing,Jian-Bin Chen,Hai-Bin Xue and Kang-Xian Guo

1 Department of Physics,College of Physics and Optoelectronics,Taiyuan University of Technology,Taiyuan 030024,China

2 Key Laboratory of Advanced Transducers and Intelligent Control System,Ministry of Education and Shanxi Province,Taiyuan 030024,China

3 Department of Physics,School of Physics and Materials Science,Guangzhou University,Guangzhou 510006,China

Abstract We theoretically study the four-wave mixing(FWM)response in a quantum dot-cavity coupling system,where a two-level quantum dot(QD)is placed in an optical cavity while the cavity mode is coupled to the nanomechanical resonator via radiation pressure.The influences of the QDcavity coupling strength,the Rabi coupling strength of the QD,and the power of the pump light on the FWM intensity are mainly considered.The numerical results show that the FWM intensity in this hybrid system can be significantly enhanced by increasing the QD-cavity coupling strength.In addition,the FWM intensity can be effectively modulated by the Rabi coupling strength and the pump power.Furthermore,the effects of the cavity decay rate and the cavitypump detuning on the FWM signal are also explored.The obtained results may have potential applications in the fields of quantum optics and quantum information science.

Keywords: four-wave mixing,quantum dot-cavity coupling system,input-output relation

1.Introduction

In the past few years,cavity optomechanics [1-4] has been subject to many theoretical and experimental attention,and a series of developments have been made.Many interesting phenomena have been researched in various cavity optomechanical systems,such as optical bistability [5-12],optomechanically induced transparency [13-18],second-order sideband [19-21],higher-order sidebands [22,23],slow and fast light [24-28],quantum ground state cooling [29-32],four-wave mixing (FWM) [33-37] and so on.

Among all the nonlinear phenomena in optomechanical systems,the FWM response is one of the focuses of research.Recently,Jiang et al [36] studied the FWM in a hybrid optomechanical system and found that the two-level system significantly modified the output fields of the cavity and thus leaded to the enhancement of the FWM intensity.Wang et al [37]studied the FWM response in a hybrid atomic optomechanical system and found that the FWM signal in such a hybrid system was significantly enhanced due to the coupling of the optical cavity and the atomic ensemble.Moreover,a two-level quantum dot (QD)-cavity coupling system has been extensively studied.Based on a nanometer cavity optomechanics with a single QD,Li et al[38]have reported on a nanometer optomechanical transistor scheme.Majumdar et al[39]theoretically analyzed the temporal dynamics of strongly coupled QD-cavity system driven by a resonant laser pulse and observed the signature of Rabi oscillation in the time-resolved response of the system.Englund et al[40] researched that ultrafast photon-photon Interaction in a strongly coupled QD-cavity system.More recently,Zhou et al[32]studied the cooling of the ground state of a nanomechanical resonator by a single-polarization optomechanical mechanism in a coupled QD-cavity system.Ali et al[41]proposed a theoretical scheme to optomechanically control coherent mode conversion of optical photons by utilizing two optically coupled hybrid semiconductor microcavities containing a QD.All these works indicate that the interaction between the QD and the cavity plays an important role in modulating the optical process in the QDcavity coupling system.

Figure 1.Schematic diagram of a two-level QD-cavity coupling system.

Motivated by these work,we study the FWM effect in a two-level QD-cavity coupling system in the present work.The numerical results obtained show that the FWM intensity in this hybrid system can be significantly enhanced by increasing the QD-cavity coupling strength.In addition,the FWM intensity can be effectively modulated by the Rabi coupling strength and the pump power.Moreover,the effects of the cavity decay rate and cavity-pump detuning on the FWM intensity are also discussed.

The paper is organized as follows.In section 2,the theoretical model of a two-level QD-cavity coupling system is introduced,the total Hamiltonian of the system is given and the nonlinear Heisenberg-Langevin equations are dealt with.Section 3 is devoted to numerical results and discussion.A summary and conclusions are given in section 4.

2.Theoretical model

The hybrid optomechanical system considered in this paper is schematically depicted in figure 1.The optical cavity of frequency ωcis driven by a strong pump laser with amplitude Epuand frequency ωpuas well as a weak probe laser with amplitude Eprand frequency ωpr,respectively.The QD,trapped into the cavity,is driven by another weak pump laser with frequency ωband Rabi coupling strength Ω.The right mirror of the optical cavity can resonate along the cavity axis with the frequency ωmdenoting as a mechanical resonator.The total Hamiltonian of the hybrid system in a frame rotating at the pump frequency ωpucan be expressed as(?=1) :

with δc=ωc-ωpu,δd=ωd-ωpu,and δ=ωpr-ωpu.In equation(1),the first term represents the energy of the optical cavity,where δcand a(a?),respectively,denote the cavitypump detuning and cavity photon annihilation (creation)operator.The second term is the energy of the QD,where δdis the QD-pump detuning,ωdis the transition frequency between the ground state∣g〉 and the excited state∣e〉 of the QD,andis the Pauli operator.Here,we have assumed that ωb=ωpufor simplicity but without loss of generality.The third term describes the coupling between the cavity mode and the QD,where gcdandσ+(σ-) ,respectively,represent the coupling strength between the cavity and the QD and the rasing(lowering)operator of the QD.The fourth and fifth terms represent the interactions between the cavity and the driving field,where,(i=pu,pr) ,Pi(i=pu,pr) is the corresponding input power,κ is the decay rate of the cavity,and δ is the detuning between the probe and pump fields.The sixth term represents the interaction between the weak pump laser with QD.The seventh term is the energy of the mechanical resonator,where b(b?)is an annihilation (creation) operator of the mechanical resonator.The last term represents the coupling term between the cavity and the mechanical resonator induced by the radiation pressure,where gcmis the coupling strength between the cavity and the mechanical resonator.

Figure 2.Displacement X0 as a function of the power of the pump field Ppu for different QD-cavity coupling strengths gcd=2π×7.5 and 2π×25 MHz.The other parameters are λ=794.98 nm,ωm=2π×15.9 MHz,rm=2π×150 Hz,gcm=2π×0.3 KHz,κ=2π×0.163 MHz,Γ1=2π×68 MHz,Γ2=Γ1/2,δc=0.5 ωm,δd=ωm,and Ω=0.

Figure 3.FWM intensity IFWM as a function of the frequency detuning δ/ωm for different QD-cavity coupling strengths (a)gcd=0,(b) gcd=2π×0.55,2π×0.65,and 2π×0.75 MHz,and(c) gcd=2π×5.5,2π×6.5,and 2π×7.5 MHz.The other parameters are λ=794.98 nm,ωm=2π×15.9 MHz,rm=2π×150 Hz,gcm=2π×0.3 KHz,κ=2π×0.163 MHz,Γ1=2π×68 MHz,Γ2=Γ1/2,δc=0.5 ωm,δd=ωm,Ω=0,Epr=0.05 Epu,and Ppu=10 nW.

Figure 4.FWM intensity IFWM as a function of the frequency detuning δ/ωm for different Rabi coupling strength (a) Ω=0,0.25Γ1,and 0.50 Γ1;(b) Ω=0.50Γ1,0.75Γ1,and 1.00Γ1.(c) The peak value of the FWM intensity IFWM at δ ≈-0.5 ωm and 0.5 ωm versus the Rabi coupling strength Ω.Here gcd=2π×7.5 MHz and other parameters are the same as in figure 3.

Figure 5.FWM intensity IFWM as a function of the frequency detuning δ/ωm for different cavity decay rate κ=2π×0.15,2π×0.45,and 2π×0.75 MHz.Here gcd=2π×7.5 MHz,Ω=0.5 Γ1,Ppu=10 nW and other parameters are the same as in figure 3.

According to the Heisenberg equation of motionand the communication relations [a,a?]=1,[b,b?]=1,[σ+,σ-] = 2σ z,and[σz,σ±]= ±σ±,the temporal evolutions of the operator a,σ-,σz,and X(which is defined ascan be obtained.In what follows,we deal with the mean response of the system to the probe field in the presence of the pump field,and let〈a〉 ,〈a?〉,〈σ-〉,〈σ+〉 ,〈σz〉 ,and〈X〉be the expectation values of operators a,a?,σ-,σ+,σz,and X,respectively.Taking the damping terms into consideration,the equations are given by

where γmis the damping rate of the mechanical resonator,Γ1the exciton spontaneous emission rate and Γ2the dephasing rate of the QD.It should be noted that the factorization assumptions 〈Xa〉 = 〈X〉〈a〉 ,〈a?a〉 = 〈a?〉〈a〉 ,〈a?σ-〉=〈a?〉〈σ-〉,and〈aσ+〉 = 〈a〉 〈σ+〉are used[42,43]in the above equations.In order to obtain the solutions of the above equations,we make the following ansatz:

Here a0,X0,andare the steady-state solutions of a,X,σ-,and σz,respectively.Upon substituting equations(6)-(9)into equations(2)-(5)and working to the lowest order in Eprbut to all orders in Epu,we can obtain

Figure 6.FWM intensity IFWM as a function of the frequency detuning δ/ωm for different pump power(a)Ppu=2,6,and 10 nW;(b) Ppu=10,14,and 18 nW.(c) The peak value of the FWM intensity IFWM at δ ≈-0.5 ωm and 0.5 ωm versus the pump power Ppu.Here gcd=2π×7.5 MHz,Ω=0.5 Γ1 and other parameters are the same as in figure 3.

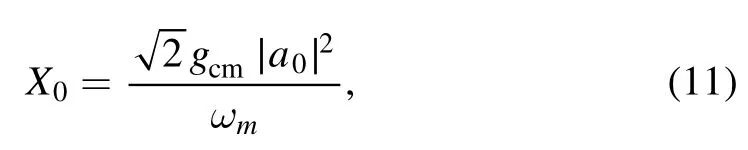
Figure 7.FWM intensity IFWM as a function of the detuning δ/ωm for different cavity-pump detuning δc=0.1 ωm,0.2 ωm,0.3 ωm,0.4 ωm,and 0.5 ωm.Here gcd=2π×7.5 MHz,Ω=0.5Γ1,Ppu=10 nW and other parameters are the same as in figure 3.

with

In order to study the optical property of the output field,we can using the input-output relation [44]

where ainand aoutare the input and output operators,respectively.In this system,we can obtain the expectation value of the output field as

Writing〈aout(t)〉as

and comparing equations (26) and (27),we can obtain the output field amplitude of the FWM as

To describe the FWM briefly,a dimensionless FWM intensity is defined as

3.Results and discussion

To illustrate the numerical results,we choose the realistic parameters of the QD-cavity coupling system as follows [11,32,45,46]: ωm=2π×15.9 MHz,rm=2 π×150 Hz,gcm=2π×0.3 KHz,κ=2π×0.163 MHz,Γ1=2π×68 MHz,Γ2=Γ1/2,and the wavelength of the pump laser λ=794.98 nm.

Figure 2 shows the displacement X0varies with the power of the pump field Ppufor different values of QD-cavity coupling strengths gcd.From this figure,it can be clearly seen that the bistable behavior not exists for that gcd=2π×7.5 MHz,and when the QD-cavity coupling strength gcdis increased to 2π×25 MHz,the bistable behavior of the system appears.Therefore,in the following discussion,the selected parameters will be selected in areas that are not in the bistable region.

In order to analyse the impact of the QD on the FWM response in the QD-cavity coupling system,figure 3 is plotted which shows the FWM spectrum versus the probe-pump detuning δ for different QD-cavity coupling strengths gcd.From figure 3(a),it can be clearly seen that in the absence of the QD,i.e.gcd=0,two weak peaks appear at δ/ωm=±1.0 in the spectrum of the FWM intensity.However,when the interaction between the cavity and the QD is considered,two new peaks are generated at δ/ωm=±0.5 as shown in figure 3(b).More importantly,these new peaks are increasing with the increase of the QD-cavity coupling strength gcd,while the peaks at δ/ωm=±1.0 have no obvious changes.For the strong coupling case,i.e.gcd＞κ,the new peaks at δ/ωm=±0.5 are so strong as to be dominant as shown in figure 3(c),and the peaks at δ/ωm=±1.0 is so weak that it can not be observed in the FWM spectrum.These results from figure 3 demonstrate that the FWM intensity is strongly dependent on the QD-cavity coupling strength gcd.To obtain strong FWM signal in the QD-cavity coupling system,large QD-cavity coupling strength is required.In the following discussion,we choose gcd=2π×7.5 MHz.

To estimate the role of the Rabi coupling strength Ω on the FWM response,the FWM intensity IFWMas a function of the normalized frequency δ/ωmis plotted for different Rabi coupling strength Ω in figures 4(a) and (b).As shown in figure 4(a),with the increase of the Rabi coupling strength Ω form 0 to 0.5Γ1,the peak values of the FWM intensity IFWMincrease as well,and obviously the peaks suffer a little shift.However,with the continuing increase of the Rabi coupling strength Ω from 0.5 to 1.0 Γ1,the peak values begin to decrease and the peaks do not shift again,which can be clearly observed in figure 4(b).The peak value of the FWM intensity at δ ≈±0.5 ωmversus the Rabi coupling strength Ω is also shown in figure 4(c),which clearly presents the dependance of the peak values on the Rabi coupling strength Ω.Obviously,the peak values of the FWM intensity reach their maxima at Ω ～0.5 Γ1.From these figures,we can conclude that only when an optimal Rabi coupling strength is chosen,can strong FWM intensity be obtained.

These phenomena above can be easily understood as follows.With the increase of the Rabi coupling strength Ω,the numbers of intracavity photon can be increased correspondingly.And as a result,the FWM process will be promoted and the peak values of the FWM intensity initially increase.Moreover,it is well known that the increasing intracavity photon number will shift the mechanical frequency and at the same time adjust the effective decay rate of the cavity [2].Therefore,at the beginning the peaks of the FWM intensity is shifted as the Rabi coupling strength Ω increases can not be observed in the FWM spectrum figure 4(a).However,when the Rabi coupling strength is larger than its optimal value 0.5Γ1,the increasing effective cavity decay rate predominates and thus the FWM process is restrained as shown in figure 4(b).To demonstrate this conclusion,the impact of the cavity decay rate κ on the FWM response in the QD-cavity coupling system is presented in figure 5,which shows the FWM intensity IFWMvursus the frequency detuning δ/ωmfor different cavity decay rate κ.It is obvious that with the increase of the cavity decay rate κ the FWM intensity is reduced significantly,which is consistent with the conclusion above.

Equally,the pump power Ppualso has an important role to play in the FWM process.In order to reveal the effect of the pump power Ppuon the FWM process,the FWM intensity IFWMas a function of the normalized frequency δ/ωmis plotted in figures 6(a)and(b)for different pump power Ppu.It is clear that increasing the pump power can promote the FWM process at first.As shown in figure 6(a),the peak values of the FWM intensity increase obviously when the pump power Ppuis tuned from 2 to 10 nW,and at the same time the peaks also have a little shift.However,as shown in figure 6(b),when the pump power Ppuis increased from 10 to 18 nW,the FWM intensity starts to decrease.To present the dependance of the FMW intensity on the pump power more clearly,the FWM intensity at δ ≈±0.5 ωmas a function of the pump power Ppuis plotted in figure 6(c).It is obvious that when the pump power Ppuis tuned to be about 10 nW,both the FWM intensity at δ ～0.5 ωmand that at δ ～-0.5 ωmreach maxima.These phenomena are consistent with the results induced by the Rabi coupling strength Ω as shown in figure 5.Similarly,we can conclude that when the pump power is optimally adjusted,strong FWM signal can be obtained in this hybrid QD-cavity system.

In order to reveal the impact of the cavity-pump detuning δcon the FWM response in the QD-cavity coupling system,the FWM intensity IFWMas a function of the probe-pump detuning δ/ωmis plotted for different cavity-pump detuning δcin figure 7.From this figure,it can be clearly observed that the spectrum of the FWM intensity can be significantly controlled by the cavity-pump detuning.As is shown,with the increase of the cavity-pump detuning,the two peaks of the FWM intensity depart from each other and their values are also effectively modulated.What is interesting is that the FWM peaks are,respectively,located at δ=δcand δ=-δc.Therefore,by tuning the cavity-pump detuning the FWM peaks can be exactly controlled.

4.Conclusion

We have theoretically investigated the FWM response in a two-level QD-cavity coupling system.The effect of the coupling strength between the QD and the cavity on the FWM generation is mainly focused on and the influences of the Rabi coupling strength,the pump power,and the cavity-pump detuning on the FWM generation are also discussed in detail.The obtained results show us that strong FWM signal can be generated in this hybrid system with large QD-cavity coupling strength.The larger the coupling strength is,the stronger the FWM signal will be.Moreover,optimizing the Rabi coupling strength and the pump power can also effectively enhance the FWM signal.In addition,the intensity and the position of the FWM peak can be effectively controlled by the cavity-pump detuning.

Acknowledgments

We are grateful to Professor Zi-Dan Wang at the University of Hong Kong.This work was supported by the National Natural Science Foundation of China(Grant Nos.11 504258,61775043 and 11805140),and the Natural Science Foundation of Shanxi Province (Grant Nos.201801D221021 and 201801D221031).

ORCID iDs