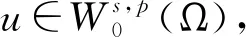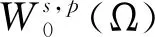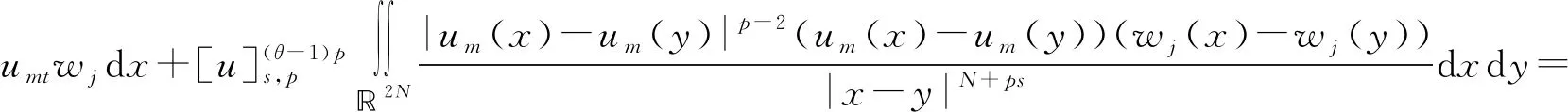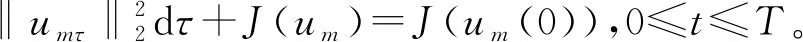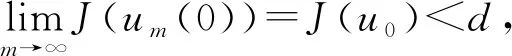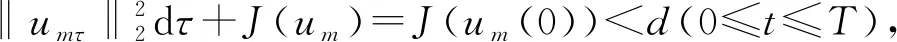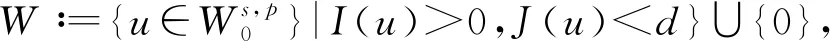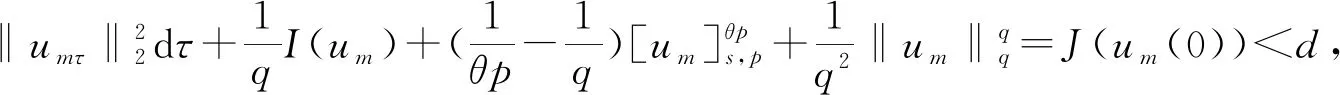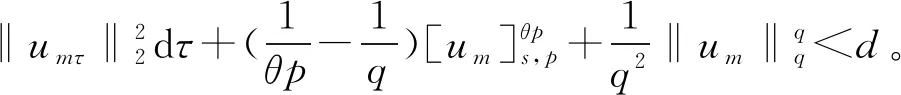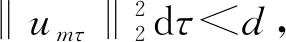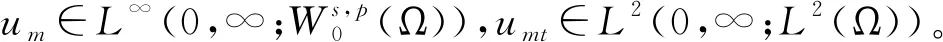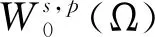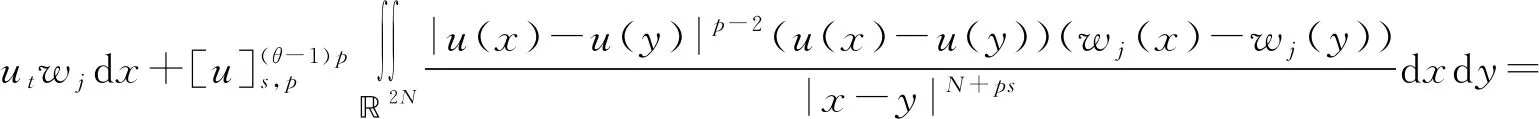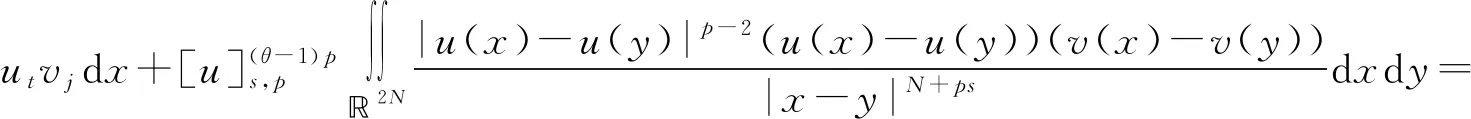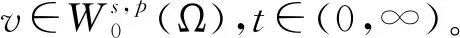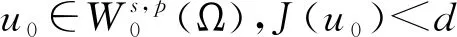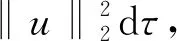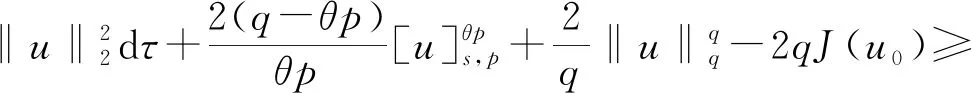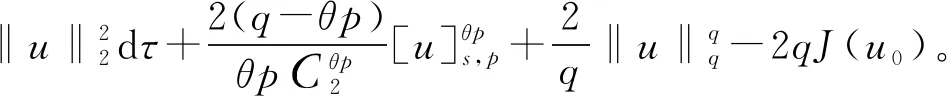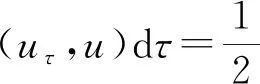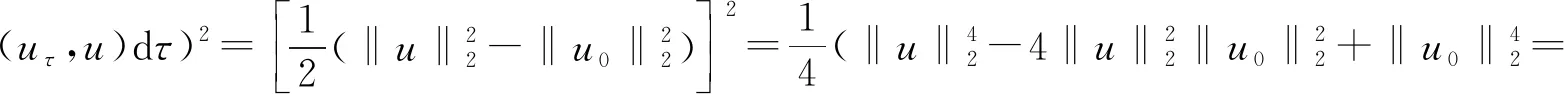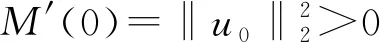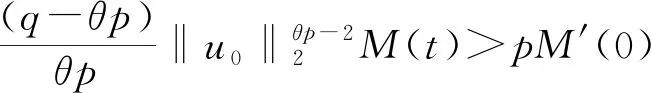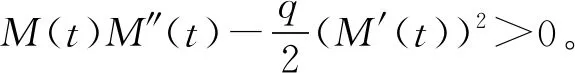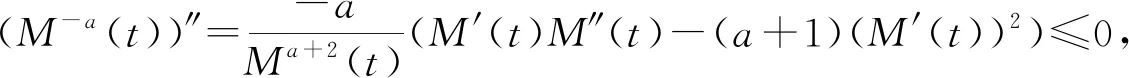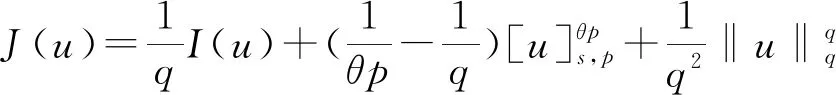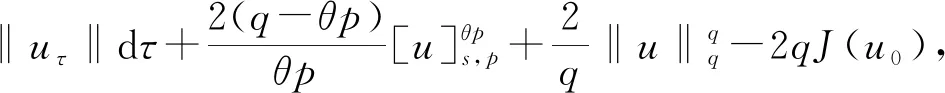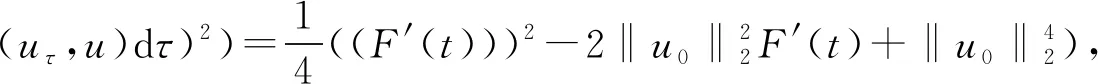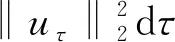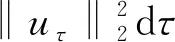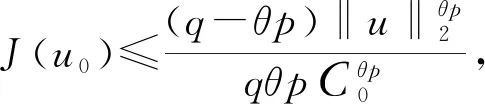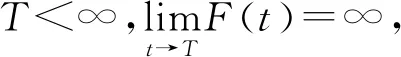一類分數階拉普拉斯方程解的存在性與爆破性
鄧啟剛,石 鵬,曾福庚
(貴州民族大學 數據科學與信息工程學院,貴陽 550025)
0 引言
分數階拉普拉斯方程相關問題的研究廣泛來源于物理、化學、生物、氣象、工程、地質等實際問題,近年來引起了學者們的廣泛關注[1-3]。本研究考慮如下分數階拉普拉斯方程
(1)
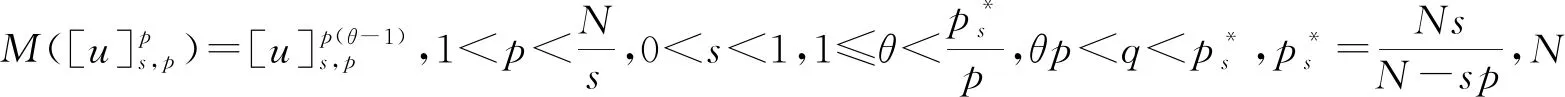
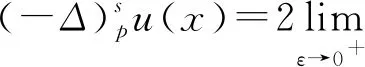
其中:Bε(x)表示一個在N上以x為圓心、ε為半徑的球;[u]s,p是Gagliarodo半范數,滿足
文獻[4]研究了一類基爾霍夫型非線性拋物方程解的存在性和爆破性,文獻[5]和文獻[6]分別研究了一個帶非局部積分-微分算子和帶基爾霍夫擴散項的解的局部存在性、全局存在性和爆破性。文獻[7]研究了一類帶對數非線性項的分數階拉普拉斯基爾霍夫方程的解的全局存在性和有限時間爆破性。在此基礎上,本研究結合變分法理論討論了上述式(1)在低初始能量J(u0) 首先定義能量泛函J(u)和Nehari泛函I(u)如下 (2) (3) 由式(2)和式(3)可知 (4) 然后定義位勢井W和相應的集合V[8]如下 下面給出以下引理。 (ⅲ)J(λu)在0≤λ≤λ*時單調遞增,在λ*≤λ≤∞時單調遞減,λ=λ*在處取到最大值; (ⅳ)當0≤λ≤λ*時,I(λu)>0;當λ*≤λ≤∞時,I(λu)<0;在λ=λ*時,有I(λ*u)=0。 (ⅱ)由于 h′(λ)=-(q-θp)λq-θp-1?Ω|u|qln|u|dx-(q-θp)λq-θp-1lnλ?Ω|u|qdx-λq-θp-1?Ω|u|qdx= λq-θp-1-((q-θp)?Ω|u|qln|u|dx-(q-θp)lnλ?Ω|u|qdx-?Ω|u|qdx)。 假設存在一個λ1使得h′(λ1)=0,則 (ⅳ)因為 (ⅰ)若0<[u]s,p (ⅱ)若I(u)≤0,則[u]s,p≥r(σ)。 證明由I(u)的定義有 證明對于u∈,有以及I(u)=0,由d的定義和引理4的結論(ⅱ),有[u]s,p≥r(σ),由于 下面給出弱解、最大存在時間、有限時間爆破的定義,并給出與之相關的一些引理。 (ⅲ)對于0≤t≤T,有 (5) 定義2 (最大存在時間) 設u(t)是式(1)中方程的解,定義u(t)的最大存在時間如下: (ⅰ)如果u(t)存在時間為[0,∞),那么T=+∞; (ⅱ)如果存在t0∈(0,∞),使得u在0 證明通過弱解的定義有 引理7 若um(t)在(0,∞)×Ω上幾乎處處收斂于u(t),則對于足夠大m,有 ?Ω|um|qln|um|dx-?Ω|u|qln|u|dx≤0。 證明由引理2可得 ?Ω|um|qln|um|dx-?Ω|u|qln|u|dx≤ |?Ω|um|qln|um|+uum|um|q-2ln|um|-uum|um|q-2ln|um|-|u|qln|u|dx|= |?Ω(um-u)um|um|q-2ln|um|+u(um|um|q-2ln|um|-u|u|q-2ln|u|)dx|≤ 因此結論成立。 引理8 若在(0,∞)×Ω中um(t)→u(t)幾乎處處成立,其中有um(t),u(t)∈W,則有 證明由于 因此結論成立。 本文主要討論低初始能量J(u0) 其中:gjm(t)∈1[0,T)(0≤t≤T,j=1,2,…,m),同時滿足故 ?Ω|um|q-2umln|um|wjdx(0≤t≤T)。 對于j=1,2,…;djm=(um(0),wj)=gim(0)是一個常數,使得式(1)中方程在L2(Ω)上有意義,且 (7) 則對于足夠大的m有 下證對于足夠大的m和t0∈[0,T],有um(x,t)∈W。 假設um(x,t)?W,則存在一個足夠大的m和t0∈[0,T],使得有um(x,t)∈?W,有I(um(t0))=0,J(um(t0))=d,因此有um(t0)∈。由于則有J(um(t0))≥d,與J(um(t0))=d矛盾。故當m→∞時,t∈[0,T]有um(x,t)∈W。 為了使m足夠大,t∈[0,T],需滿足: (9) (10) (11) 若um(t)∈W,且 ?Ω|um(t)|q-2um(t)ln|um(t)|dx≤-?Ω(|um(t)≤1|)|um(t)|q-1ln|um|(t)dx+ ?Ω(|um(t)>1|)|um(t)|q-1ln|um|(t)dx≤ 則在L∞(0,∞;L1(Ω))中|uv(t)|q-2vv(t)ln(vv(t))→|u|p-2uln|u|,在L2(0,∞;L1(Ω))中|uv(t)|q-2uv(t)ln(uv(t))→|u|p-2uln|u|。 M″(t)=2(u(t),u(t))=-2I(u), (12) (13) (14) 由式(13)、式(14)和施瓦茲不等式,可得 現在討論兩種情形: (ⅰ)若J(u0)≤0,那么有 (ii)若0 由施瓦茲不等式,有1預備知識
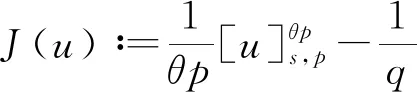
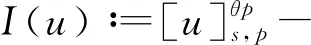

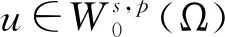

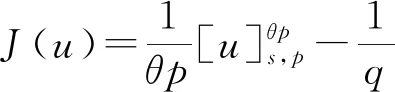
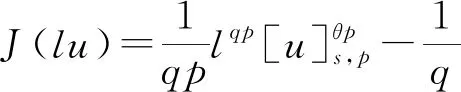
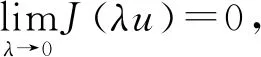
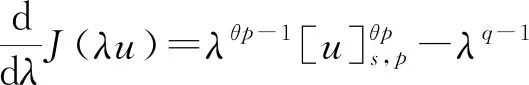
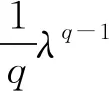
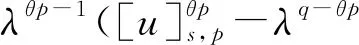
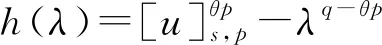
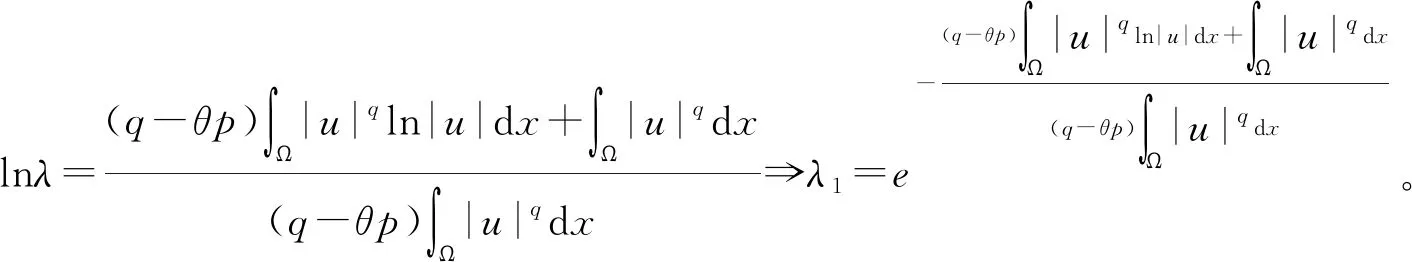
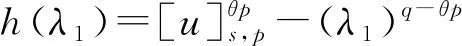
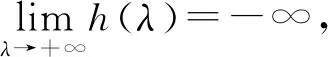

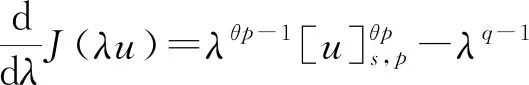
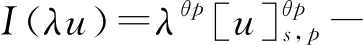
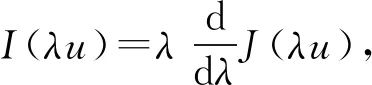

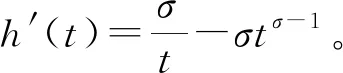
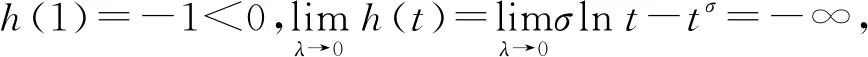
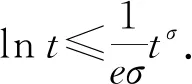
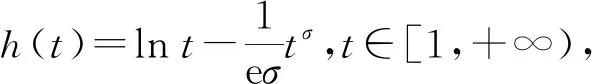
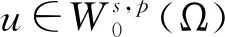
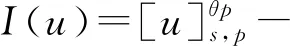
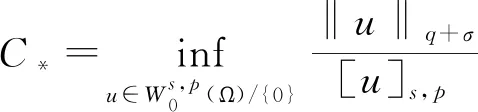
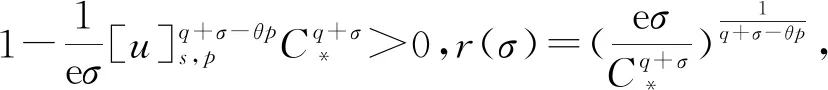
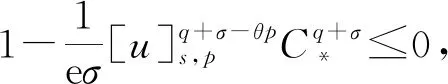
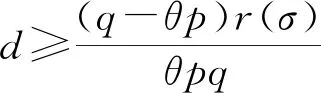
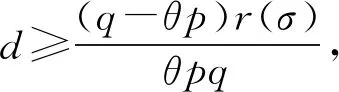
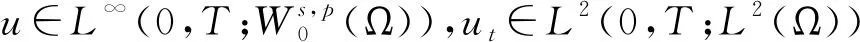
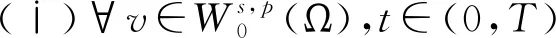
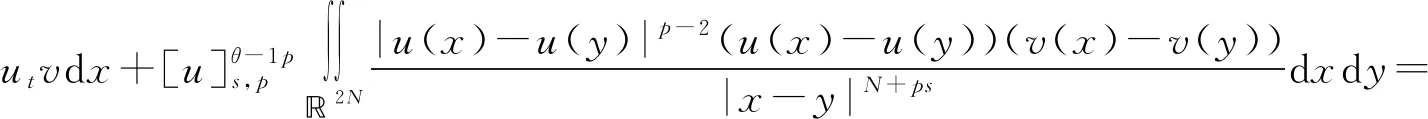
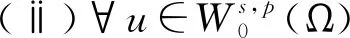
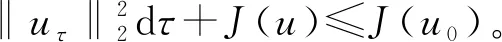
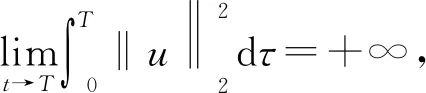
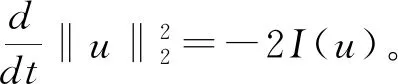
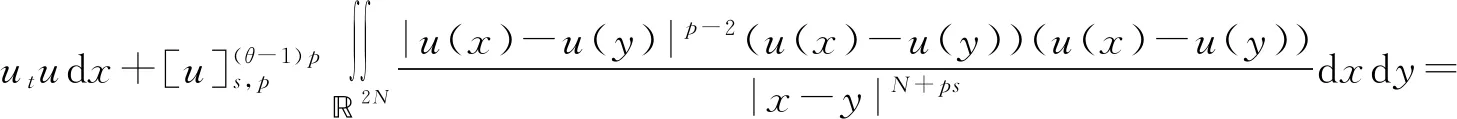

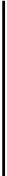
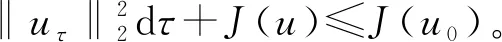
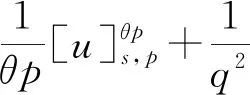
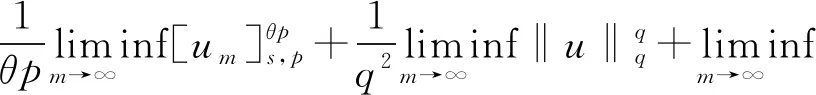
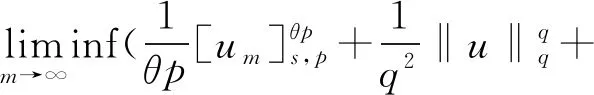
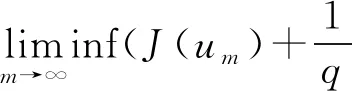
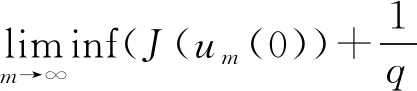
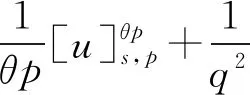
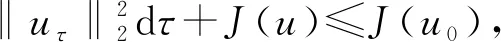
2 主要結果和證明