計算方法對鋼筋混凝土圓管涵受力分析的影響研究

唐楊 王國煒 鐘華棟 唐彬

1.五峰土家族自治縣農村公路管理所 宜昌443413

2.濟南金衢公路勘察設計研究有限公司 250101

3.四川攜源建筑工程設計有限公司 成都610000

4.湖北屹峽峰建設工程有限公司 宜昌443000

引言

鋼筋混凝土圓管涵是較為常見的涵洞形式，由于方便裝配式施工、圬工數量少、造價低［1］，廣泛應用于公路工程和農田水利工程［2-4］。

查閱相關文獻發現：鋼筋混凝土圓管涵的受力分析大都通過在土體與鋼筋混凝土圓管涵的交界面設置接觸對考慮土體與鋼筋混凝土圓管涵的接觸非線性。許慶虎［5］、馬祖橋［6］、顏丹青［7］均以某鋼筋混凝土圓管涵為研究對象，采用ANSYS有限元軟件建立實體有限元模型，在土體和鋼筋混凝土圓管涵的表面設置面-面接觸單元來反映土體與鋼筋混凝土圓管涵的相互作用。當考慮土體與鋼筋混凝土圓管涵的接觸非線性時，計算較為復雜，收斂較為困難。與鋼筋混凝土圓管涵較為相似的波紋鋼管涵，在其計算分析中，駱志紅［8］、彭立［9］等學者忽略了波紋鋼板與土體的滑移，不考慮接觸非線性，直接將波紋鋼板與土體共節點處理，而鋼筋混凝土圓管涵的受力分析較少采用這種簡化處理。

本文以某農村公路的鋼筋混凝土圓管涵為研究對象，采用考慮接觸非線性的計算方法和共節點處理的簡化方法分別對其進行計算分析，對比兩種計算方法下鋼筋混凝土圓管涵受力情況的差異。

1 工程概況

某農村公路的鋼筋混凝土圓管涵縱向長10m，圓形截面的直徑為1.2m，其中壁厚0.1m。鋼筋混凝土圓管涵的縱向有32 根φ8 通長鋼筋和2 根10 螺旋鋼筋，螺旋鋼筋旋轉一周的縱向伸長量為a ＝13.3cm，鋼筋混凝土圓管涵的配筋情況如圖1 所示。

圖1 鋼筋混凝土圓管涵（單位： cm）Fig.1 Reinforced concrete circular pipe culvert（unit：cm）

2 分析思路

鋼筋混凝土圓管涵的有限元模型采用Midas FEA建立。鋼筋的本構模型考慮為彈性模型，彈性模量為210GPa，容重為78.5kN／m3，泊松比為0.3。鋼筋混凝土圓管涵采用C30 混凝土，混凝土的本構模型考慮為總應變裂縫模型，彈性模量為30000MPa，容重為25kN／m3，泊松比為0.2，受拉函數采用常數函數，受壓函數采用Thorenfeldt函數，其受壓應力-應變關系如圖2 所示，圖中fp為混凝土的抗壓強度標準值。土體的本構模型采用摩爾-庫侖模型，彈性模量為81MPa，容重為19.3kN／m3，泊松比為0.25，粘聚力為118kPa，摩擦角為22°，剪膨脹角為0°。

圖2 混凝土受壓本構關系Fig.2 Concrete compression constitutive relation

根據圣維南原理，取一定土體范圍進行建模，圓管涵四周的土體至少為一倍管徑的厚度［8］，鋼筋混凝土圓管涵左、右側的土體厚度取2.4m，上、下側的土體厚度取1.4m，鋼筋混凝土圓管涵的管軸方向取1.0m，鋼筋混凝土圓管涵和土體的幾何模型建立后采用自由網格劃分技術劃分為四面體單元。螺旋鋼筋采用面面交線的方法建立幾何模型［10］，然后采用自由網格劃分技術劃分為鋼筋單元，不考慮鋼筋與混凝土的滑移［11］。模型一不考慮鋼筋混凝土圓管涵與土體的接觸非線性，將鋼筋混凝土圓管涵與土體共節點連接；模型二設置接觸對，將鋼筋混凝土圓管涵與土體考慮為面-面接觸，將圓管涵的外表面定義為主面，土體接觸面定義為從屬面，貫穿類型選擇軸對稱一般接觸，表示兩個面粘接在一起，可以適用于計算中反復粘接、分離的情況，圓管涵與土體之間的靜態摩擦因子設置為0.4，剛度比例因子設置為1.0。模型一和模型二表面上看相同，但在鋼筋混凝土圓管涵與土體的邊界上處理不同，處理為接觸時邊界的同一位置有兩個節點，處理為共節點時邊界的同一位置僅有一個節點。有限元模型如圖3 所示，共計70486 個單元。

圖3 有限元模型Fig.3 Finite element model

在邊界上，將土體的底部固結，左、右兩側限制水平位移。在荷載上考慮自重和汽車荷載。汽車荷載施加于鋼筋混凝土圓管涵上部土體的表面，采用面壓力施加，面壓力的范圍考慮為一個輪載的接觸面積0.6m ×0.8m，壓力總量偏大地考慮為120kN。分析工況設置為非線性靜力分析，計算方法采用Newton Rapson 迭代法，荷載步驟數設置為5，最大迭代步驟數設置為100。

3 兩種計算模型的對比分析

3.1 變形分析

為了方便分析鋼筋混凝土圓管涵的變形，對鋼筋混凝土圓管涵的節點位置進行編號，圓管涵中間截面的最左側節點編號為1，最右側節點編號為2，最上側節點編號為3，最下側節點編號為4，節點分布示意如圖4 所示。

通過計算，對模型一和模型二分別提取鋼筋混凝土圓管涵節點1 和節點2 的水平位移如圖5a 所示，提取鋼筋混凝土圓管涵節點3 和節點4 的豎向位移如圖5b所示。將節點2的水平位移減去節點1 的水平位移得到鋼筋混凝土圓管涵的水平變形，將節點4 的豎向位移減去節點3 的豎向位移得到鋼筋混凝土圓管涵的豎向變形，鋼筋混凝土圓管涵的變形計算結果如圖5c所示。水平位移由節點1 指向節點2 為正值，豎向位移由節點4 指向節點3 為正值。

由圖5a 和5b 可以看出，在相同的節點位置，模型二的位移值大于模型一的位移值，隨著荷載系數的增加，模型一與模型二的位移差值越來越大。由圖5c 可以看出，模型二的圓管涵結構變形大于模型一的圓管涵結構變形，隨著荷載系數的增加，模型一與模型二的結構變形差值越來越大。當荷載系數為1 時，模型一的水平變形為0.29mm，豎向變形為0.32mm；模型二的水平變形為0.38mm，豎向變形為0.41mm。由此可見，模型二的水平變形比模型一的水平變形大31.03%，模型二的豎向變形比模型一的豎向變形大28.13%。根據以上計算結果發現：模型二中鋼筋混凝土圓管涵的結構變形比模型一大。

圖4 節點分布示意Fig.4 Node distribution diagram

圖5 鋼筋混凝土圓管涵的位移和變形Fig.5 Displacement and deformation of reinforced concrete pipe culvert

3.2 應力分析

通過計算，對模型一和模型二分別提取鋼筋混凝土圓管涵的第一主應力最大值如圖6a 所示，鋼筋的應力最大值如圖6b 所示，其中拉應力為正，壓應力為負。

圖6 鋼筋混凝土圓管涵的應力Fig.6 Stress of reinforced concrete pipe culvert

由圖6a 可以看出，隨著荷載系數的增加，鋼筋混凝土圓管涵的第一主拉應力和第一主壓應力最大值均呈現增大趨勢，第一主拉應力最大值的增長速度大于第一主壓應力最大值的增長速度。當荷載系數達到0.8 時，模型一的主拉應力最大值接近C30 混凝土的抗拉強度標準值，模型二的主拉應力最大值達到C30 混凝土的抗拉強度標準值。當荷載系數達到1.0 時，模型一的主拉應力最大值才達到C30 混凝土的抗拉強度標準值。由圖6b 可以看出，隨著荷載系數的增加，鋼筋混凝土圓管涵的鋼筋應力最大值呈現增大的趨勢，模型二的鋼筋應力最大值大于模型一的鋼筋應力最大值。當荷載系數為1 時，模型一的鋼筋拉應力最大值為21.38MPa，鋼筋壓應力最大值為23.90MPa；模型二的鋼筋拉應力最大值為31.19MPa，鋼筋壓應力最大值為27.84MPa；模型二的鋼筋拉應力最大值比模型一大45.88%，鋼筋壓應力最大值比模型一大16.49%。

由于模型一和模型二的第一主應力分布較為相似，僅提取荷載系數為1 時模型二的第一主應力云圖如圖7 所示。由圖7 可以看出，鋼筋混凝土圓管涵的主拉應力最大值主要出現在左、右側的外緣和上、下側的內緣。

圖7 荷載系數為1 時模型二的第一主應力（單位： N／mm2）Fig.7 The first principal stress of model 2 when the load factor is 1（unit：N／mm2）

3.3 裂縫寬度分析

通過計算，對模型一和模型二分別提取鋼筋混凝土圓管涵的裂縫寬度如圖8 所示，模型二在荷載系數為0.8 和1.0 時的裂縫分布如圖9 所示。由圖9 可以看出，模型一在荷載系數為1.0時才出現混凝土裂縫，主要出現在鋼筋混凝土圓管涵上、下側的內緣，其裂縫寬度最大值為1.81 ×10-3mm。結合圖8 可以看出，模型二在荷載系數為0.8 時就出現混凝土裂縫，剛開始主要出現在鋼筋混凝土圓管涵上、下側的內緣，然后出現在左、右側的外緣，之后裂縫沿內、外環線擴展，荷載系數為1.0 時裂縫寬度最大值為3.97 ×10-3mm，為模型一裂縫寬度最大值的2.19 倍。

圖8 鋼筋混凝土圓管涵的裂縫寬度Fig.8 Crack width of reinforced concrete pipe culvert

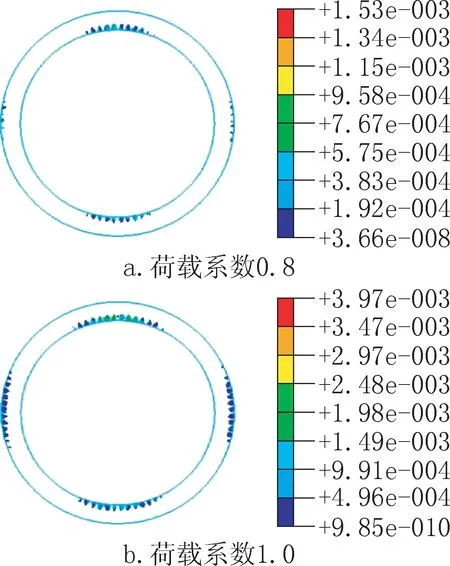
圖9 模型二的裂縫分布（單位： mm）Fig.9 Crack distribution of model 2（unit：mm）

3.4 接觸力分析

模型一將鋼筋混凝土圓管涵與土體之間考慮為共節點無法得到接觸力的分析結果，在此僅對模型二提取鋼筋混凝土圓管涵與土體的水平接觸力最大值和豎直接觸力最大值如圖10 所示。荷載系數為1.0 時的水平接觸力和豎直接觸力分布如圖11 所示。

圖10 鋼筋混凝土圓管涵的接觸力Fig.10 Contact force of reinforced concrete pipe culvert

由圖10 和圖11 可以看出，鋼筋混凝土圓管涵左側和右側的水平接觸力最大值較為接近，上側的水平接觸力比下側的水平接觸力小；上側的豎直接觸力最大值比下側的豎直接觸力最大值大。當荷載系數為1.0 時，上側的接觸力最大值為231.17N，下側的接觸力最大值為186.24N，上側的接觸力最大值比下側的接觸力最大值大24.12%。當荷載系數為1.0 時，水平接觸力最大值為58.70N，豎直接觸力最大值為231.17N，為水平接觸力最大值的3.94 倍。

圖11 荷載系數為1 時的接觸力分布（單位： N）Fig.11 Contact force distribution when the load factor is 1（unit：N）

4 結論

以某農村公路的鋼筋混凝土圓管涵為工程背景，對比分析了兩種不同計算方式下鋼筋混凝土圓管涵的變形、應力、裂縫大小和分布，可以得到以下結論。

1.考慮鋼筋混凝土圓管涵與土體的接觸非線性時，鋼筋混凝土圓管涵的水平變形相比不考慮接觸非線性時增大31.03%，豎向變形相比不考慮接觸非線性時增大28.13%，即考慮鋼筋混凝土圓管涵與土體的接觸非線性時計算得到的結構變形偏大。

2.無論是否考慮鋼筋混凝土圓管涵與土體的接觸非線性，混凝土的第一主應力最大值均達到其抗拉強度標準值，但考慮鋼筋混凝土圓管涵與土體的接觸非線性時，普通鋼筋的拉應力比不考慮接觸非線性時增大45.88%，壓應力比不考慮接觸非線性時增大16.49%。

3.考慮鋼筋混凝土圓管涵與土體的接觸非線性時，鋼筋混凝土圓管涵的裂縫寬度是不考慮接觸非線性時的2.19 倍，但無論是否考慮鋼筋混凝土圓管涵與土體的接觸非線性，其裂縫寬度均在允許范圍之內。

4.考慮鋼筋混凝土圓管涵與土體的接觸非線性時，可以得到鋼筋混凝土圓管涵與土體的接觸力，更加符合結構的真實受力狀態。由于鋼筋混凝土圓管涵多為帶裂縫工作，結構計算中必須考慮材料非線性，在此基礎上再考慮接觸非線性將顯著增加計算的收斂難度，故而在對計算結果要求不是很高或硬件條件達不到時，也可以不考慮鋼筋混凝土圓管涵與土體的接觸非線性，采用共節點簡化接觸關系，但其計算結果是偏于危險的，需要對計算結果考慮一個放大系數才可使用。從計算結果來看，考慮2作為放大系數較為合適。