相對誤差最小二乘法的TDLAS氣體濃度標定曲線擬合

陳 昊，鞠 昱，韓 立，常 洋

1.中國科學院電工研究所，北京 100190 2.中國科學院大學，北京 100049 3.北京航天易聯科技發展有限公司，北京 100176

引 言

可調諧半導體激光光譜(tunable diode laser absorption spectroscopy，TDLAS)是利用氣體分子對激光信號的選頻吸收，計算入射光與出射光的光功率變化，實現對待測氣體濃度的定量檢測。近年來大量學者對TDLAS技術進行了研究，相較于其他光譜檢測技術，它具有高靈敏度、高分辨率、實時監測、便攜性好、小型化等優點，在工業環保、醫療檢測、氣象監測等領域得到了廣泛的應用[1-3]。

TDLAS氣體傳感器出廠前需要進行標定，擬合出光強透射率對數與標定濃度的對應關系曲線，擬合結果影響傳感器的測量精度[4]。最小二乘法(least squares method，LSA)是目前常用的擬合算法，它是以絕對誤差的平方和最小作為評價標準，無法對相對誤差進行約束，而實際測量中的數據誤差往往基于相對誤差，即被測量值越大所允許的實際絕對誤差也越大。采用最小二乘法擬合會導致TDLAS氣體傳感器的標定曲線在低濃度量程下的相對誤差偏大，限制了標定量程。此外，TDLAS氣體傳感器標定時一般采用多項式作為目標函數進行擬合，這只能保證較小濃度范圍內的測量精度，量程外的測量誤差急劇增大。對于大量程標定則需要推導完整的光強透射率對數與氣體濃度關系式，以此作為目標函數進行擬合，提高整個量程范圍內的測量精度[5-7]。為此提出了一種基于相對誤差意義下的氣體濃度標定算法，能夠解決上述問題，提高TDLAS氣體傳感器測量精度。

通過分析了TDLAS技術中大量程濃度標定的問題，提出了基于相對誤差最小二乘法的擬合算法，推導了完整的光強透射率對數與氣體濃度關系式，搭建了TDLAS水汽標定平臺，對1%～50%VOL的水汽濃度標定曲線進行了誤差分析，驗證了本文提出的相對誤差最小二乘法的可靠性，提高了TDLAS氣體傳感器的檢測精度。

1 TDLAS標定原理

TDLAS技術理論基礎是Beer-Lambert定律，它描述了一束特定頻率的激光進入氣體樣品前后的光強變化[8]，如式(1)所示。

(1)

式(1)中，It為穿過待測氣體后的透射光光強，I0為入射光強，α(ν)為吸收系數，c為待測氣體的濃度，L為光吸收路徑長度。

TDLAS氣體傳感器的標定原理是利用擬合算法得到光強透射率對數Ratio與標準氣體濃度c之間的關系曲線，通過實測的Ratio來反演待測氣體濃度。Ratio的表達式如式(2)所示。

(2)

根據式(2)可知，Ratio與氣體濃度c是一次函數關系，標定時采用一次函數作為目標函數具有較好的相關性。但這忽略了氣體濃度對吸收系數α(ν)的影響，在大量程標定時，吸收系數受氣體濃度變化影響，Ratio與氣體濃度c不再是一次函數關系。因此需要考慮氣體濃度對吸收系數的影響，推導出完整的Ratio與氣體濃度c的關系式，以此作為目標函數進行標定曲線的擬合。

吸收系數α(ν)表達式如式(3)

(3)

式(3)中，gL(ν)為洛倫茲線型函數，S為吸收譜線強度，N為單位體積內氣體分子總數，α=NS/πγL，為氣體吸收峰中心位置(ν=ν0)的吸收系數，γL為氣體吸收譜線半寬高，它與氣體濃度大小有關，表達式如式(4)。

(4)

式(4)，n為溫度系數，p0和T0為標準氣壓和標準溫度，γair是空氣吸收譜線半高寬，γself是待測氣體吸收譜線半高寬，由式(4)可知，γL與氣體濃度值相關。

當ν=ν0，即在吸收峰的中心位置，將式(3)和式(4)代入式(2)，得到氣體濃度c與Ratio的關系式。

(5)

式(5)中，KS(T)是吸收譜線強度關于溫度的修正系數，S0是標準氣壓溫度下的吸收譜線強度，N0是標準氣壓溫度下的單位體積分子數。圖1是氣體濃度與光強透射率對數的關系曲線模擬圖。

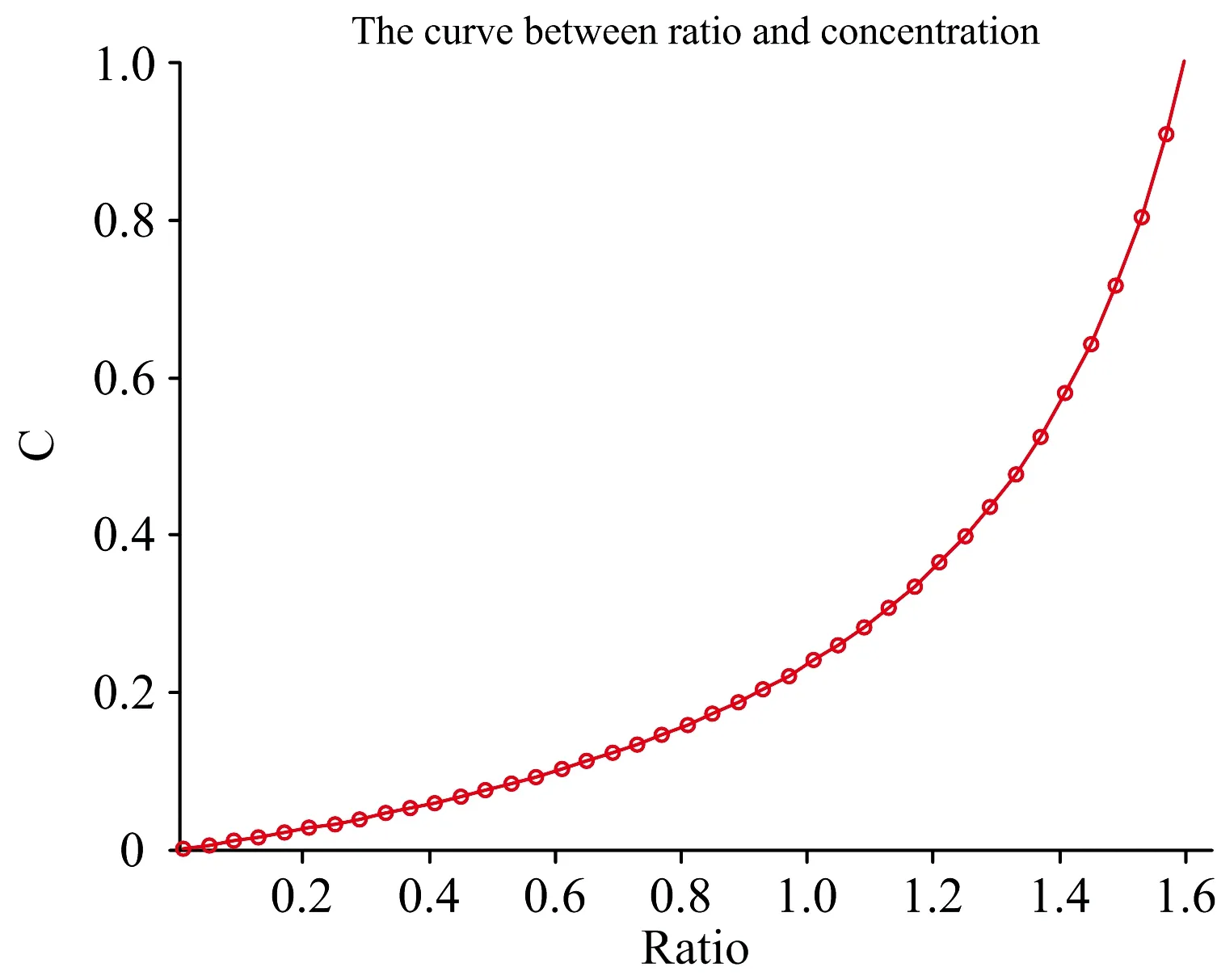
圖1 氣體濃度與光強透射率對數的關系曲線模擬圖Fig.1 The relation of ratio and concentration

對式(5)簡化，并對光強透射率對數Ratio進行溫度修正，得到目標函數如式(6)

(6)

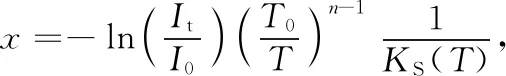
以式(6)作為目標函數擬合能夠提高標定曲線的擬合相關度，但目前常用的最小二乘法擬合是基于絕對誤差意義，它是依據等精度數據而言，誤差分布服從均值為0的正態分布。對TDLAS氣體傳感器進行大量程標定時，考慮的更多是相對誤差，即高濃度下標定所允許的絕對誤差也更大，研究相對誤差意義下的標定曲線更具有實際應用意義。

2 相對誤差最小二乘法

最小二乘法是一個最優化的問題，它是通過最小化誤差的平方和尋找數據的最佳函數匹配，基于相對誤差最小二乘法(relative error least squares method，RELSA)則是尋找相對誤差的平方和最小來尋求最優解，迭代方法采用高斯-牛頓迭代法(Gauss-Newton iteration method)，該法使用泰勒級數展開式去近似地代替目標函數，然后通過多次迭代，多次修正待定系數，使待定系數不斷逼近目標函數的最佳待定系數，使原函數的相對誤差平方和達到最小[9-10]。

對于相對誤差最小二乘問題，目標函數為

(7)

目的是尋找最優解p，使得相對誤差平方和S最小。

(8)

(9)

(10)

其中，k是迭代次數，Δp是迭代矢量，每次迭代函數是線性的，在pk處用泰勒級數展開。

(11)

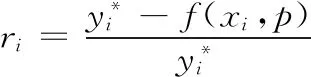
(12)

式(12)中，Δyi是第k次迭代的殘差，將式(12)代入式(9)，得到

(JTJ)Δp=JTΔyi

(13)

式(13)是矩陣形式，J是目標函數的雅克比矩陣，求解式(13)便可以獲得迭代增量Δp，代入式(10)得到最終的迭代公式。

(14)

整個算法流程如圖2所示。

3 實驗與結果討論

實驗用雅士林DHS-100恒溫恒濕箱來產生大量程水汽標定濃度，以Vaisala HMT337在線濕度檢測儀的測量值作為標定濃度，自主研發的TDLAS濕度傳感器選擇波數為7 306.752 1 cm-1的水汽吸收峰(表1所示)，吸收強度為1.8×10-20cm-1·(molec·cm-2)-1，氣室的光路長為50 mm。實驗時，將HMT337在線濕度檢測儀的濕度探頭以及自研TDLAS濕度傳感器濕度探頭和溫度探頭放入恒溫恒濕箱中，通過對恒溫恒濕箱的控制來完成對不同濃度的水汽標定。

表1 Hitran數據庫Table 1 Hitran database

實驗測量了1%～50%標定濃度下的Ratio值，目標函數選擇多項式函數和Ratio-C關系式(6)，對比了最小二乘法(LSA)和相對誤差最小二乘法(RELSA)的擬合結果。

3.1 多項式為目標函數的擬合結果

多項式擬合時，目標函數選用了三次多項式和五次多項式兩種算法進行擬合，圖3是兩種算法進行多項式擬合的標定曲線圖，圖4是擬合值與標定濃度的相對誤差分布圖，表2是最小二乘法和相對誤差最小二乘法的相對誤差分布圖。

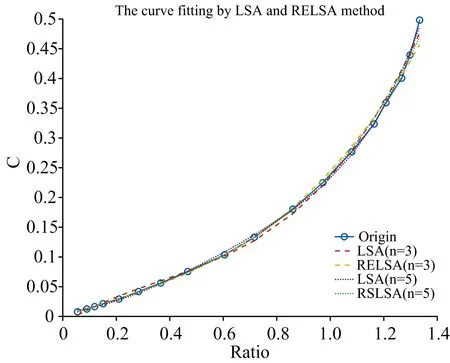
圖3 多項式擬合曲線Fig.3 Polynomial curve fitting

由圖4可知，采用最小二乘法擬合時，在低濃度量程下出現較大的相對誤差，高濃度量程下相對誤差變小；采用相對誤差最小二乘法時，整個量程下的相對誤差曲線比較平穩。在表2中也得到驗證，以三次多項式擬合為例，相對誤差最小二乘法下的最大相對誤差為0.082 8，遠低于最小二乘法的0.722 9，同時相對誤差的標準差為0.030 3，明顯優于最小二乘法的0.187 6，五次多項式的擬合結果也表明相對誤差最小二乘法的擬合結果更優。

圖4 多項式擬合誤差分布Fig.4 The distribution of relative error in polynomial fitting

表2 多項式為目標函數的擬合誤差統計Table 2 The error analysis in polynomial fitting

3.2 Ratio-C關系式為目標函數的擬合結果

以Ratio-C關系式(6)作為目標函數進行擬合時，為了使迭代計算盡快收斂，根據表1的Hitran數據，將初值設定為p(1)=0.85，p(2)=0.093，p(3)=0.51，兩種算法的擬合曲線如圖5所示，圖6是擬合曲線相對誤差分布圖。

圖5 Ratio-C關系式擬合曲線Fig.5 Fitting curves with Ratio-C formula

由圖6所示，從Ratio-C關系式作為目標函數的擬合誤差分布結果上看，采用最小二乘法在低濃度量程下出現了較大的相對誤差，高濃度量程下逐漸減小；采用相對誤差最小二乘法整個誤差分布趨于平穩，這與多項式為目標函數的擬合結果相似。表3可知，相對誤差最小二乘法的最大相對誤差為0.049 4，相對誤差標準差為0.023 7，均優于最小二乘法的最大相對誤差0.160 4和相對誤差標準差0.057 2。結合多項式擬合結果，以Ratio-C關系式作為目標函數，采用相對誤差最小二乘法的擬合結果最好，相對誤差在±5%以內，最大相對誤差和相對誤差標準差都最小，擬合結果最優。

圖6 Ratio-C關系式擬合誤差分布Fig.6 The distribution of relative error in Ratio-C formula fitting

表3 Ratio-C關系式為目標函數的擬合誤差統計Table 3 The error analysis in Ratio-C formula fitting

4 結 論

針對TDLAS氣體傳感器的標定，推導了完整的光強透射率對數與氣體濃度關系式，以此作為目標函數，提出了基于相對誤差最小二乘法對標定曲線進行擬合。實驗結果表明：采用最小二乘法擬合時，在低濃度量程下會出現較大的相對誤差，高濃度量程下相對誤差逐漸減小，無法保證整個大量程下測量精度要求；采用相對誤差最小二乘法擬合時，在整個大量程范圍下的相對誤差波動比較小，相對誤差曲線比較平穩，最大相對誤差和相對誤差標準差都遠小于最小二乘法的擬合結果；以Ratio-C關系式作為目標函數，采用相對誤差最小二乘法進行擬合標定時，最大相對誤差為0.049 4，相對誤差標準差為0.023 7，遠優于最小二乘法的擬合結果，驗證了相對誤差最小二乘法的標定算法可靠性，提高了TDLAS氣體傳感器的測量精度。