高鐵接觸網轉換柱承力索拉出值偏差原因分析及改進

李安政

0 引言

腕臂結構是電氣化鐵路接觸網的重要組成部分，腕臂安裝的質量直接影響接觸網工程的整體質量。為了提高腕臂安裝精度，我國時速300 km以上的高速鐵路接觸網系統均采用科學計算和工廠化預配的方式，其中科學計算是最關鍵的一環。目前，我國主流的腕臂計算理論和方法大多只針對腕臂結構的幾何特點進行分析，而忽視了接觸網的力學特性，由此造成施工中出現較多難以解釋的誤差。如果錯誤地將這些誤差歸結為施工誤差，而未探究計算方面的原因，將會大大增加接觸網調整工作量，而大量的調整會破壞接觸網的統一性，進而影響接觸網工程的整體質量。

1 京沈客專轉換柱承力索拉出值偏差原因分析

京沈客專設計時速為350 km，在接觸網工程施工過程中，施工人員發現轉換柱處承力索拉出值出現偏差，如表1所示。

從表1中看出，接觸線架線前，承力索的拉出值偏差較小，非工作支誤差為35 mm，工作支誤差為2 mm。然而在接觸線架線后，承力索拉出值產生了較大的偏差，其中非支拉出值誤差達84 mm，工支拉出值誤差為13 mm。由此可見，腕臂結構在架線后受到了線材帶來的張力影響，導致承力索拉出值誤差增大。經分析，承力索拉出值的主要影響因素有：

表1 1033#轉換柱承力索拉出值統計 mm

（1）支柱斜率。經測量，架線前支柱傾斜為0 mm。架線后，支柱因受線材張力的影響，在上腕臂底座相對軌面位置向田野側傾斜14 mm，如圖1所示。由于支柱傾斜造成了拉出值變化14 mm，對非工作支和工作支拉出值均產生影響。

（2）雙腕臂底座變形。經測量，架線前雙腕臂底座變形為0 mm。架線后，腕臂底座因受線材張力的影響，向田野側產生變形，如圖2所示。非支腕臂底座變形4 mm，工支由于受力小，腕臂底座無變形。由于雙腕臂底座變形造成拉出值變化4 mm，只對非支拉出值產生影響。

（3）支柱扭曲。經測量，架線前支柱扭曲變形為0 mm。架線后，支柱因受到非支和工支不平衡力矩的影響向一側扭曲，在腕臂上底座處的扭曲值為7 mm，如圖3所示。

圖1 支柱受力傾斜示意圖

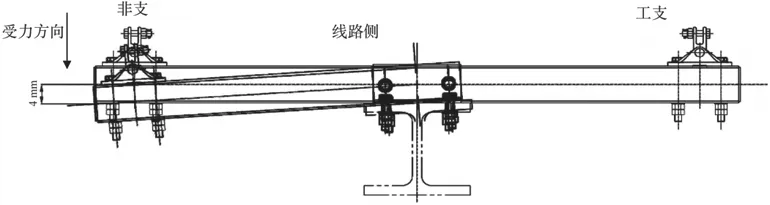
圖2 雙腕臂底座受力變形示意圖

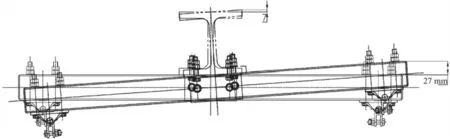
圖3 支柱扭曲變形示意圖

綜合以上幾項因素對拉出值造成的影響：

（1）對非工作支拉出值的影響為14 + 4 + 27 =45 mm，對拉出值進行修正，a= 266 + 45 = 311 mm，與架線前的測量結果315 mm相差4 mm；

（2）對工作支拉出值的影響為14 - 27 = -13 mm，對拉出值進行修正，a= 163 - 13 = 150 mm，與架線前的測量結果148 mm相差2 mm。

2 改進措施

根據接觸網施工工序，腕臂安裝在架線之前完成，因此在腕臂計算階段，支柱傾斜、底座彎曲、支柱扭曲等數據均是在不受力的情況下測量，計算得到的腕臂數據不能反映受力后發生的變化情況。

為使計算結果準確，須對不受力情況下的測量數據進行力學補償。由于上述變形均為材料的彈性變形，因此補償的依據為“胡克定律”，即“材料在彈性變形階段，其應力和應變成正比例關系，該比例系數稱為彈性模量”，具體補償過程如下：

（1）計算導致材料變形的力或力矩的大小。例如，導致支柱傾斜的力為F，張力分析見圖4。

圖4 線材對支柱的張力分析

已知參數：A點拉出值a1、B點拉出值a2、C點限界Xj、跨距L、承力索張力Tc。以上參數均為設計參數或可測量參數。 分析圖4中的力F得出

根據京沈客專設計情況及現場測量結果：Xj=3.1 m，a2= 0.35 m，a1= 0，L= 48 m，Tc= 21 kN。將結果代入式（1）可得F= 1.66 kN，即承力索對支柱的作用力為1.66 kN。

（2）計算彈性模量k。經測量，受力后轉換柱向田野側傾斜Q= 14 mm，根據胡克定律得出鋼柱傾斜的彈性模量k=Q/F= 8.4 mm/ kN。

（3）修正原始測量參數。假設原測量的支柱斜率為xl、上底座高度為H，則修正后的支柱傾斜量為Q=xlgH+kgF。式中力F在不同的情況下可出現多種可能，例如直線段、曲內、曲外、絕緣錨段關節、非絕緣錨段關節等情況下力F均不相同，需要逐一分析。式（1）計算的是直線區段非絕緣錨段關節的情況。

（4）采用修正后的測量參數進行幾何計算。對原始測量參數進行修正后再進行幾何計算，即可消除因受力帶來的影響，得到的結果更加準確。

以上力學分析是以支柱傾斜受力為例，同理，腕臂底座受力變形、支柱受力矩影響扭曲均可按照上述方法進行修正補償，本文不再進行詳細論述。

3 結語

接觸網系統結構關系高速鐵路工程的質量和安全，應引起足夠重視。通過力學分析可知，承力索拉出值偏差問題并非個別現象，其在接觸網工程中普遍存在，尤其是對于線材張力更大的高鐵項目將更為突出。

在京沈客專施工中采取了改進計算方法的措施，可以克服承力索拉出值偏差的問題，但是該措施仍然存在缺陷，例如彈性模量k取值為經驗近似值，缺乏充分的理論依據。后續建議采用ANSYS建模的方法對不同情況下的受力進行仿真分析，并對此進行更為深入的研究。