大型浮船塢浮態魯棒控制分析

董明海， 韓晨健， 趙 陳， 郭永升

(1.浙江國際海運職業技術學院，浙江 舟山 316021；2.中國船級社 舟山辦事處，浙江 舟山 316052；3.上海船舶工藝研究所 舟山船舶工程研究中心，浙江 舟山 316021)

0 引 言

魯棒控制涉及眾多領域，涉及線性系統、時變系統、非線性系統、分布參數系統、離散系統等，作為魯棒控制技術研究模型基礎的線性分式變換(Linear Fractional Transformation,LFT)所能表示的不確定系統也十分廣泛。不確定性不僅包含參數不確定性，而且包括噪聲、擾動、非線性、未建模動態特性等豐富內容。目前，通常以狀態方程中系數矩陣的線性攝動作為出發點，即認為不確定性與狀態方程的系數矩陣呈線性關系，然后以此為基礎進行控制系統的魯棒分析與設計，但在實際問題中參數與狀態方程系數矩陣之間的關系并不總是呈線性關系。浮船塢的設計主要依據各船級社的相關規范[1]。浮船塢在海上停泊或作業時，受到風浪流的干擾產生橫搖，浮態控制系統目的在于抑制風浪流干擾，減少塢體橫搖，控制浮態，確保其安全。以 30 000 t 舉力浮船塢為例，采用魯棒控制系統分析與設計方法，對其浮態的控制系統設計和魯棒控制設計進行分析。浮船塢如圖1所示。

圖1 浮船塢

1 舉力浮船塢概況

30 000 t舉力浮船塢為整體式鋼質浮塢，箱形船體，艏艉船底斜切，承載甲板無脊弧有梁拱，方形舭部鋼質焊接結構。塢墻由頂甲板+骨架、內外塢墻+骨架、安全甲板+骨架、橫向艙壁+骨架以及垂直桁等構件組成。 整個塢墻均為縱骨架式。由橫艙壁及垂直桁組成橫向強肋骨圈，共設有32 個壓載水艙、2個污水艙和2個污油艙。其主要用于 30 000 t 及以下的船舶維修，入級中國船級社(CCS)。在遮蔽海域應用時，船塢可用于托舉船舶作業，其構件的外形尺寸及重心高度應滿足CCS規范關于浮船塢的穩性與干舷的相關要求。該塢主尺度如表1所示。

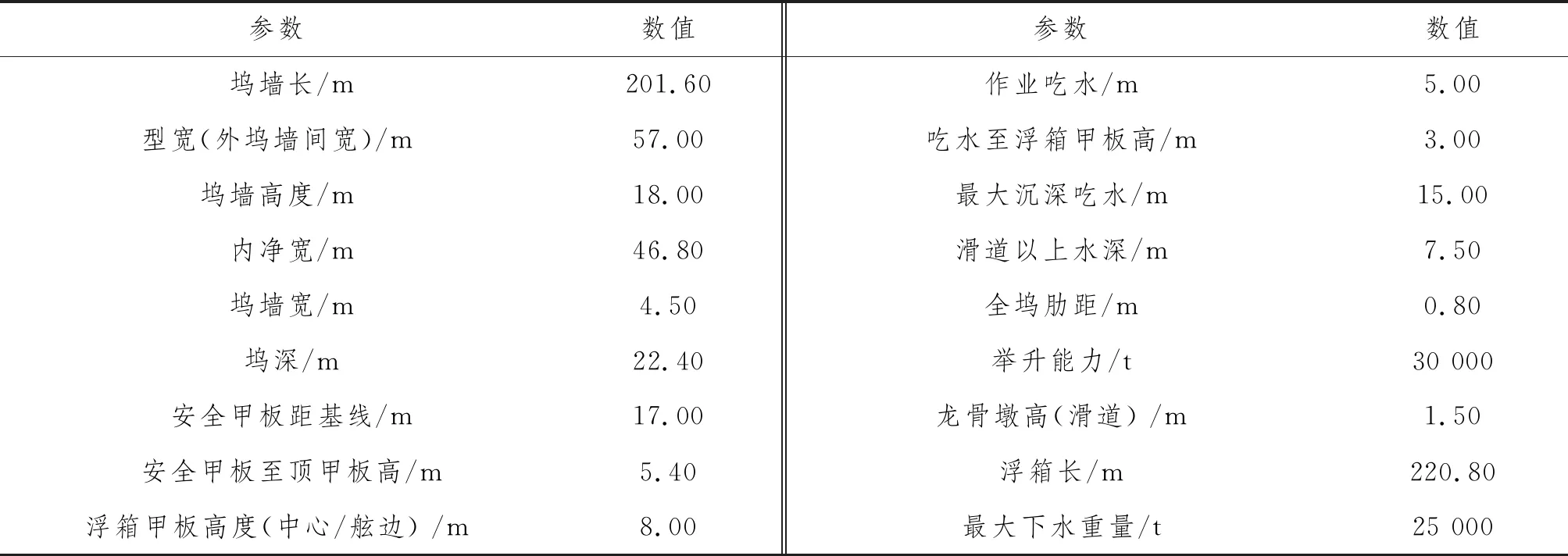
表1 浮船塢主尺度及主要參數

2 舉力浮船塢浮態魯棒控制設計思路

2.1 設計思路

浮船塢浮態控制系統的設計基于敏感度極小化的思想進行[2-3]，可分成3部分：塢體機械組合體、隨動系統和控制部分，具體組成如圖2所示。

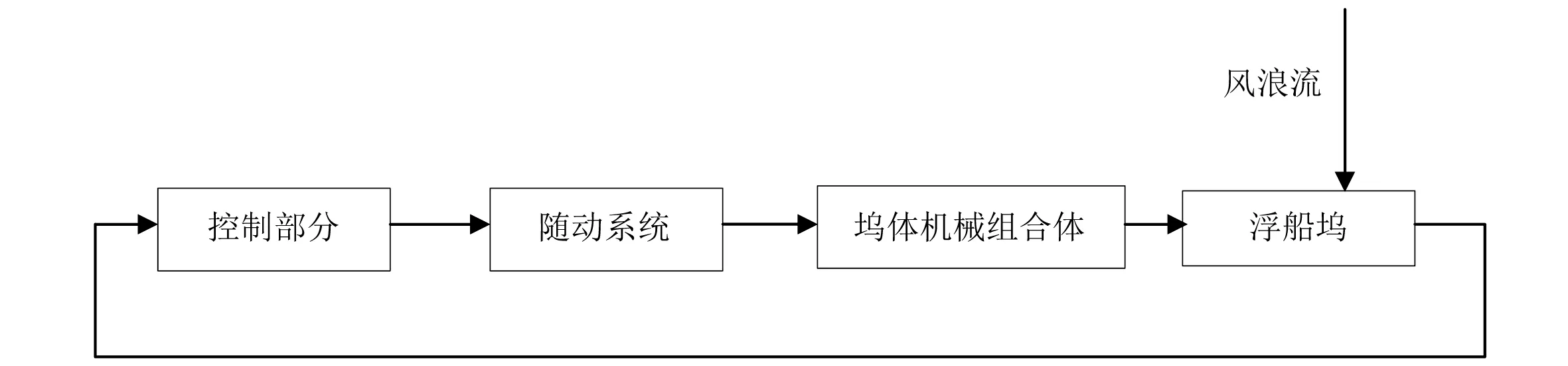
圖2 浮態控制系統組成

根據靈敏度函數S設計典型反饋系統，控制部分具有較高輸出靈敏性和準確度，靈敏度函數計算式為

(1)

式中：G為浮船塢的橫搖傳遞函數；K為控制器，目標系統下為定值。

假定系統受到的不確定外干擾信號不是一個固定的信號，而是某個已知信號集合：

{d∶d=Wx,x∈H2,‖x‖2≤1}

(2)

式中：d為風浪流干擾信號；W為經驗系數；x為振變量；H2為目標函數取得最優控制的極值。設計要求在信號集合中最壞干擾信號d的作用下，使系統在控制器的作用下輸出能量‖y‖2最小。由于y=Sd=WSx，因此這一要求等價于

(3)

式(3)即轉變為使加權靈敏度函數的極值范數極小化。由于敏感度函數S是開環特性的相對偏差到閉環特性相對偏差的傳遞函數，因此極小化S也可以使閉環特性的偏差抑制在盡可能小的范圍內。設計控制器K，使閉環系統穩定且加權敏感度函數WS的極值范數極小化。

2.2 浮態控制系統

在利用靈敏度極小化問題化作極值標準控制(見圖3)進行浮船塢浮體控制系統設計中會先遇到輸入干擾抑制問題[4]。為解決這一問題，引入系統模型轉換方法，將浮船塢控制系統的輸入干擾轉換為輸出干擾，再轉換為極值優化問題的標準形式，以求解具有輸入干擾的極值優化問題，具體做法是利用系統方框圖的等效原則，通過轉換將浮船塢浮態控制系統的風浪流輸入干擾轉換為廣義風浪流輸出干擾，這就使外界干擾以等效的浮船塢橫搖角的形式出現。

圖3 模型轉換前后的浮船塢浮態控制系統

設定塢體機械組合體傳遞函數為h，浮船塢的橫搖角為φ，則根據控制理論，可求出橫搖角φ對風浪流干擾的靈敏度函數

(4)

設定GK、GB分別為從參考信號r到橫搖角的開環橫搖傳遞函數和閉環橫搖傳遞函數，ΔGK為相應真實開環橫搖傳遞函數與標稱開環橫搖傳遞函數的偏差，ΔGB為相應真實閉環橫搖傳遞函數與標稱閉環橫搖傳遞函數的偏差，則可推導得

(5)

可見，S與開環特征相對偏差ΔGK/GK到閉環特性相對偏差ΔGB/GB的增益1/(1+KhG)只相差1個標稱的船體本身的橫搖傳遞函數。因此，極小化S不僅反映了對風浪流橫搖干擾的抑制要求，而且反映了抑制模型振動對系統的影響要求。

極小化橫搖角φ對風浪流干擾d的靈敏度函數S的極值范數，既可達到抑制風浪流干擾的減搖目的，又可使閉環特性偏差抑制在盡可能小的范圍內。

3 魯棒控制設計

以30 000 t舉力浮船塢為研究對象，其主要參數如下：排水量D為25 000 t，固有橫搖周期T為11 s，初穩心高h1為5.409 m，無因次阻尼2Nu為0.28，橫搖轉動慣量Ix為65 564×104kg·m2，橫搖附加慣量ΔIx=850×103kg·m2。其中，橫搖附加質量是按切片理論計算波浪頻率0.35～2.17共28個頻率點的附加質量平均值。

浮船塢橫搖運動方程式為

(6)

式中：C為作用在塢體上的橫搖力矩。

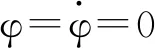
(7)

在塢體機械組合體的作用下，作用在塢體上的橫搖力矩包括風浪流的干擾力矩Cw和壓載系統產生的穩定力矩Cf，即

C=Cw+Cf=Cw+Cfaα

(8)

式中：Cfa為支撐力矩；α為浮船塢法線與水平面的夾角。

從而得到浮船塢在塢體機械組合體包括系泊設施作用下的線性傳遞函數為

(9)

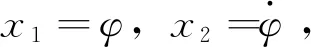
(10)

式中：

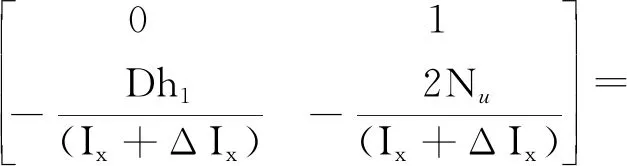
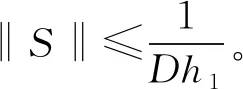
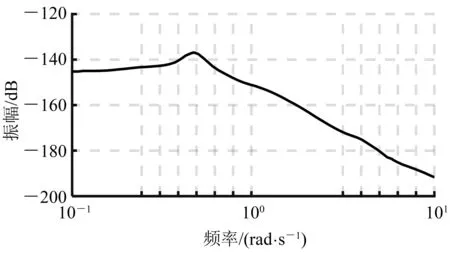
圖4 浮船塢橫搖頻率特性

浮船塢的橫搖特性是二階振蕩環節，在頻率ω=0.57 rad/s時有1個諧振峰，浮船塢在該頻率處放大橫搖。風浪的能量主要集中在0.30～0.57 rad/s的頻段內，在ω約0.70 rad/s時達到極值，因此，隨機風浪流的主要作用頻帶和浮船塢橫搖傳遞函數的頻帶相當。在選擇橫搖角φ對風浪流橫搖干擾d的靈敏度函數S的權函數時，考慮到海浪能量譜特性，同時考慮塢體橫搖特性在0.57 rad/s處有諧振峰，所選擇的權函數應使S在諧振區內有大幅度的衰減。權函數須根據物理意義經反復地選擇校核才能夠最終選定[6]。

4 系統仿真

對直接基于靈敏度函數極小化思想設計的浮船塢橫搖減搖控制系統進行仿真，檢驗上述分析與設計，為了使仿真具有代表性和充分反映各種外載荷情況，海情有義波高取值5.2 m，浪向角為30°、60°、90°、120°和150°，給出控制器的浮船塢橫搖減搖控制系統的仿真結果數據分析，如表2所示。在表2中：開環和閉環的STD(φ)為橫搖角的均方差；STD(αf)為減搖控制系統均方差；減搖率為開環橫搖角均方差與閉環橫搖均方差的差占開環橫搖角均方差的百分比。

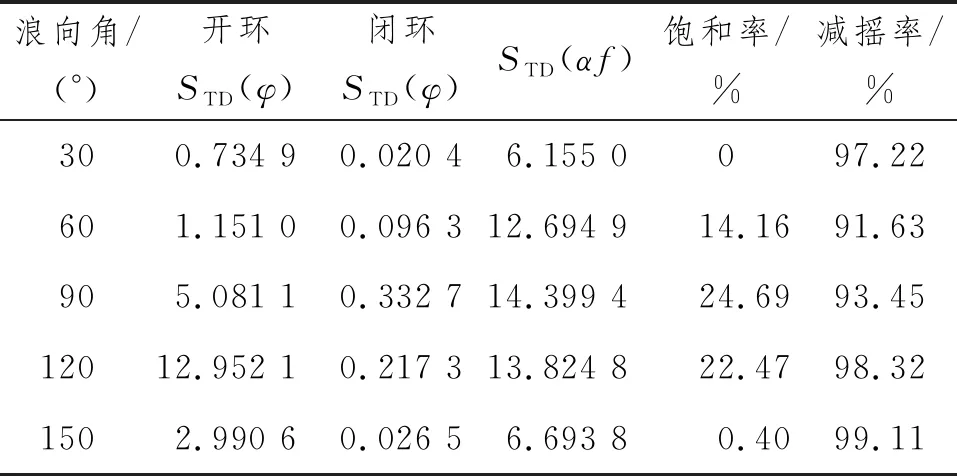
表2 不同浪向浮船塢橫搖仿真結果統計(有義波高5.2 m)

當有義波高為5.2 m時，開環、閉環橫搖角在不同浪向角下的仿真曲線如圖5～圖14所示。

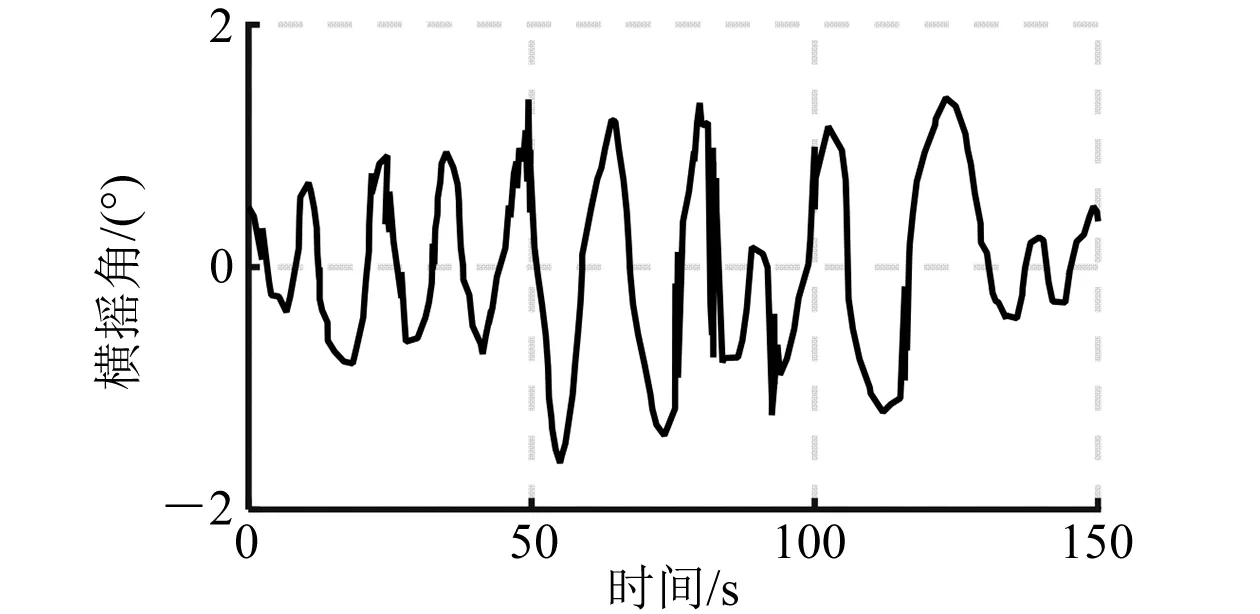
圖5 開環橫搖角仿真曲線(30°)

圖6 閉環橫搖角仿真曲線(30°)

圖7 開環橫搖角仿真曲線(60°)

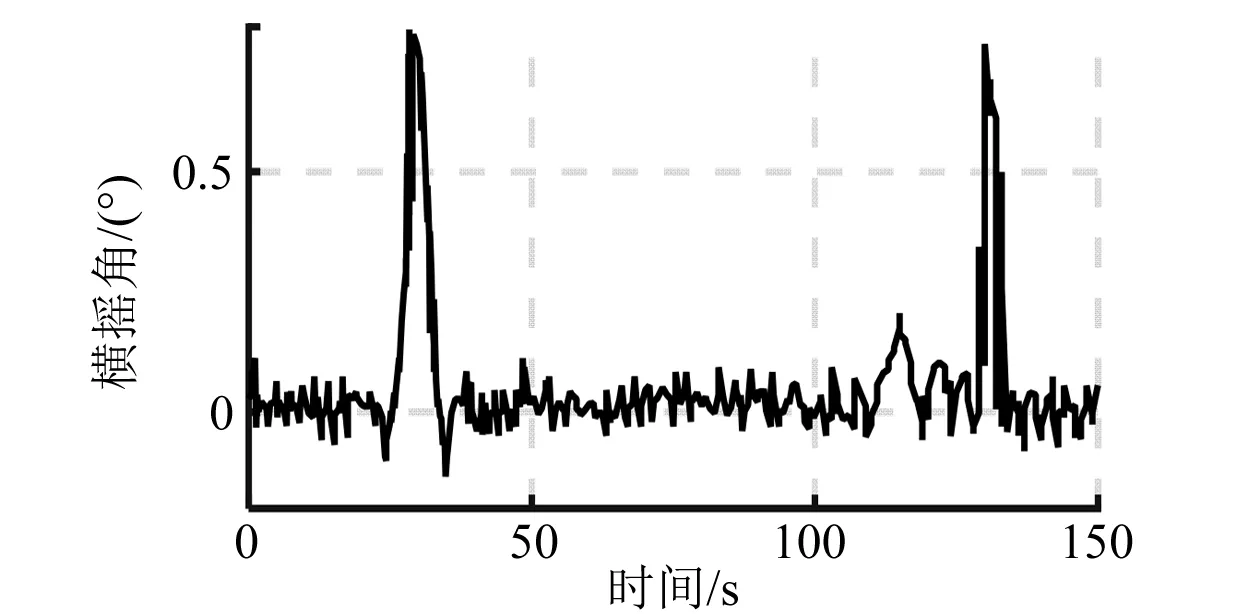
圖8 閉環橫搖角仿真曲線(60°)

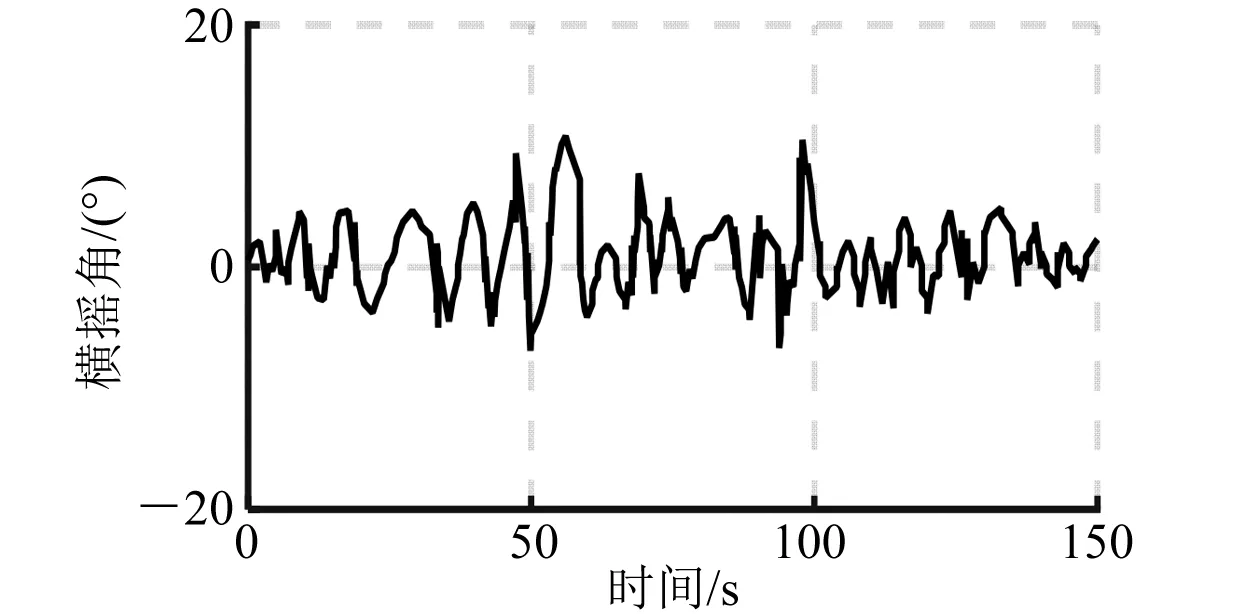
圖9 開環橫搖角仿真曲線(90°)

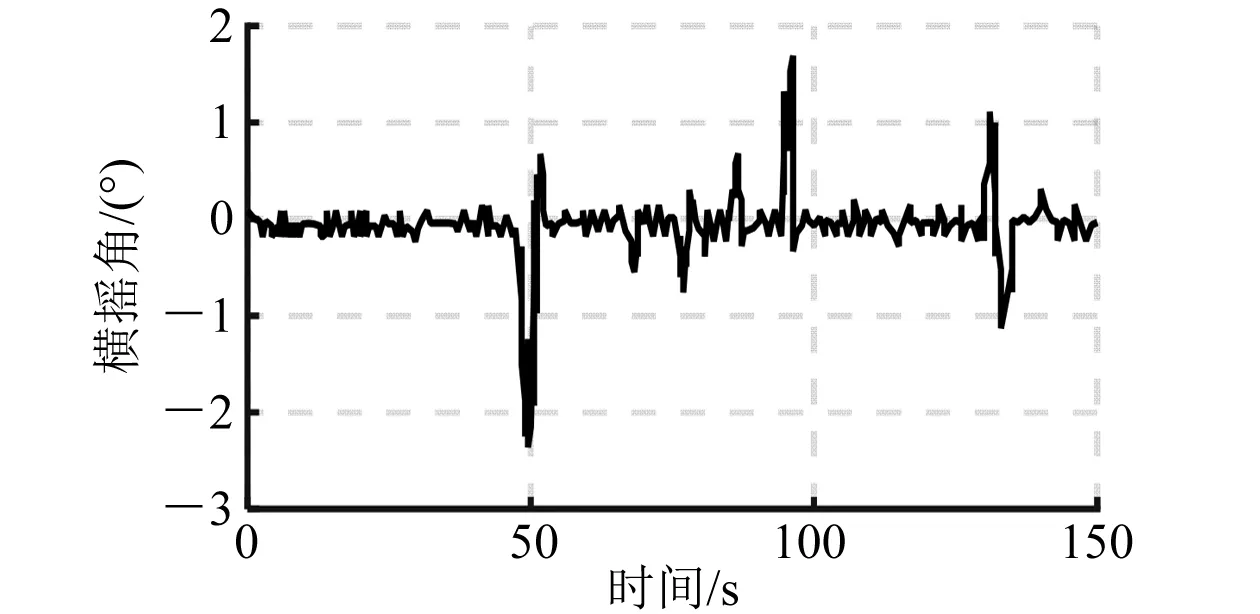
圖10 閉環橫搖角仿真曲線(90°)

圖11 開環橫搖角仿真曲線(120°)

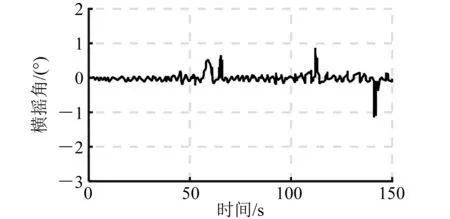
圖12 閉環橫搖角仿真曲線(120°)

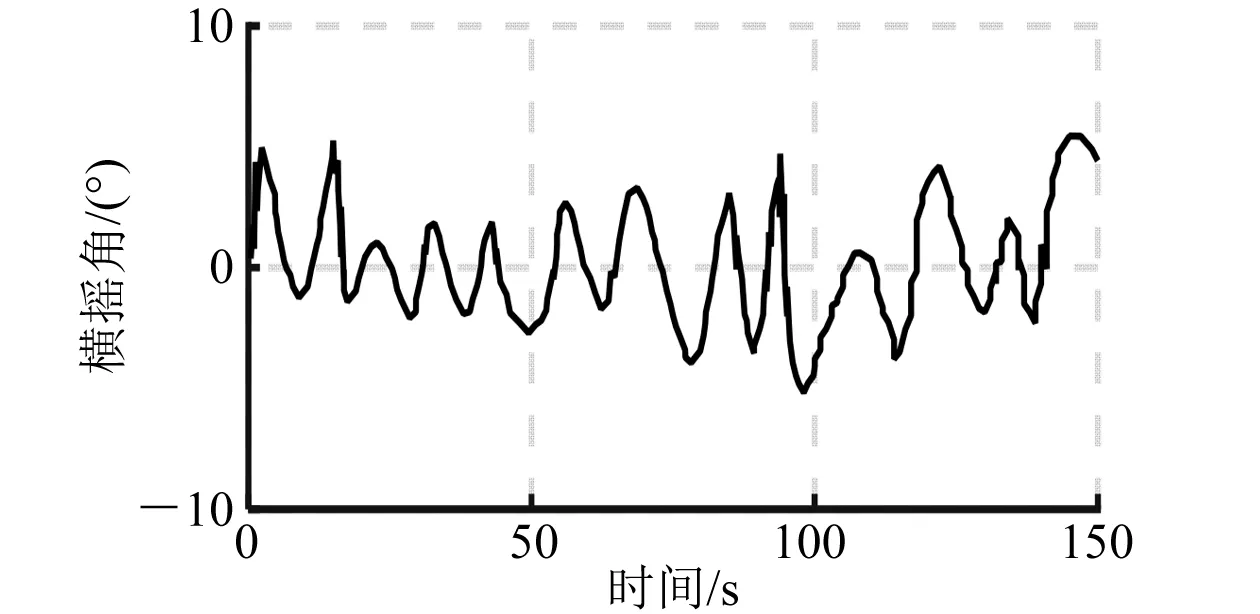
圖13 開環橫搖角仿真曲線(150°)

圖14 閉環橫搖角仿真曲線(150°)

由上述仿真曲線和數據分析可以看出：利用H∞理論設計的浮船塢橫搖減搖控制器，在有義波高5.2 m不同浪向角下，都能很好地抑制隨機海浪對浮船塢浮態的影響，有效減少橫搖。

5 結 語

30 000 t舉力浮船塢在控制器的控制下，降低對海浪干擾的抑制要求，這樣的目的是為浮船塢壓載系統和系泊系統聯合減搖做準備。由于浮船塢本身運動的特性，風浪流對浮船塢的橫搖運動影響較大，給出魯棒控制系統的設計方法，采用模型仿真與運動參數仿真，結果充分證明該系統具有良好的魯棒性，可為大型浮船塢系泊設計、壓載水系統設計和浮態控制、檢測等提供一定的參考。