高階微分方程邊值問題正解的存在性
2021-05-10 02:30:08達佳麗張麗娟
四川師范大學學報(自然科學版) 2021年3期
達佳麗, 王 婷, 張麗娟
(西北師范大學知行學院 數學系,甘肅 蘭州730070)

本文將利用文獻[1]中已有的Green函數,給出它的上下界估計,然后借助不動點指數去討論(1)式正解的存在性,再利用錐拉伸與壓縮不動點定理討論(2)式存在正解時λ的范圍.
1 預備知識
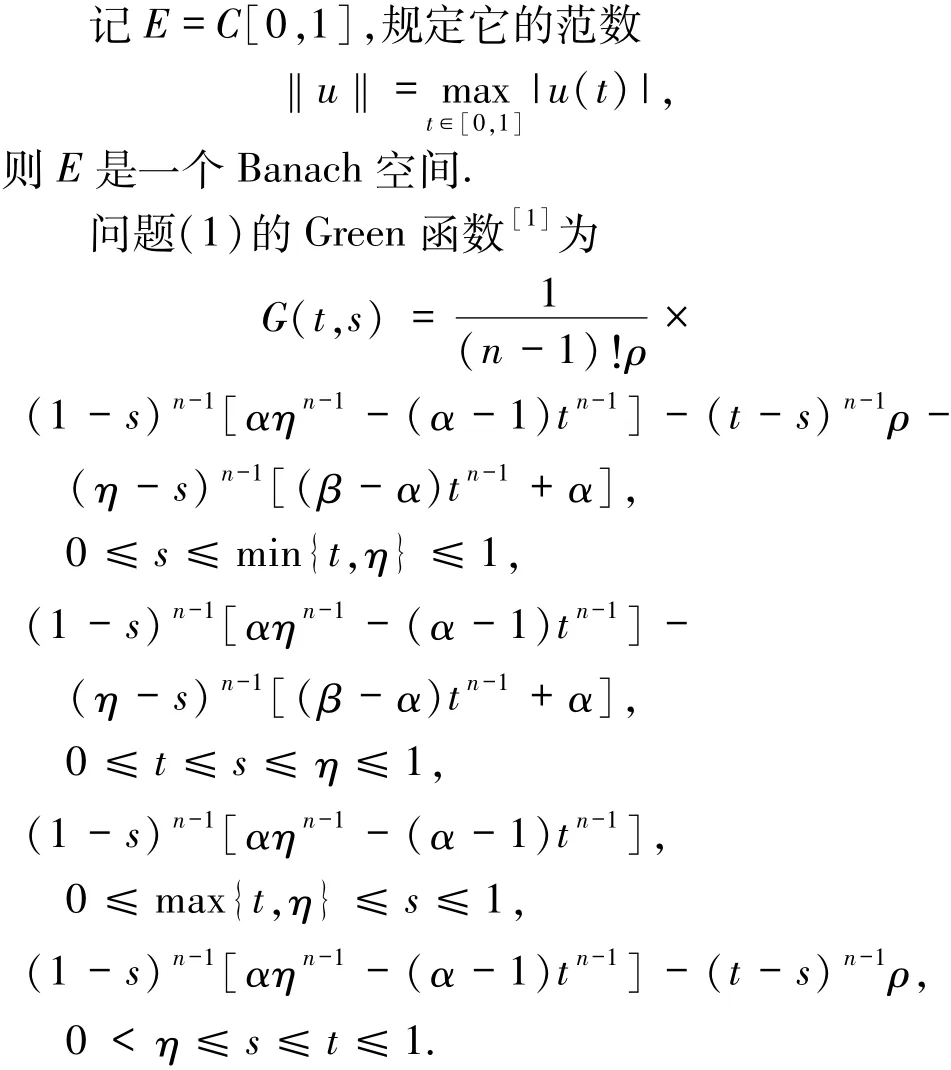
定義算子T:P→P,


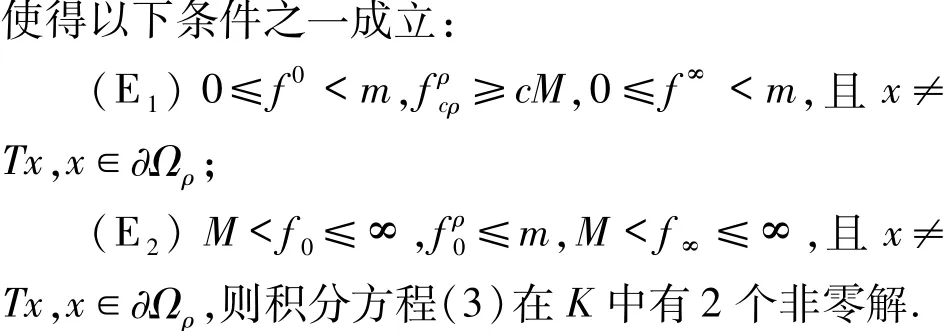
本文主要用到推論1.1和推論1.2.
2 主要結果




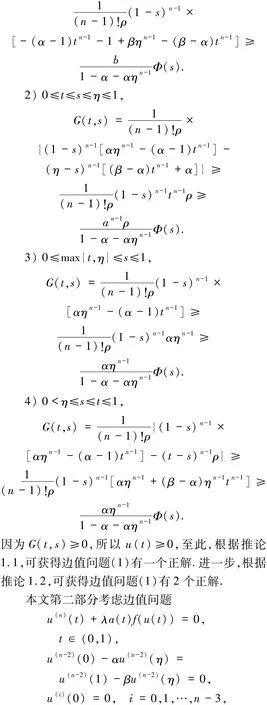
其中η∈(0,1),α,β≥0.參數λ>0,
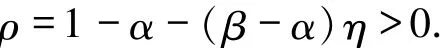
應用錐拉伸與壓縮不動點定理討論使得正解存在的λ的范圍.
其Green函數為

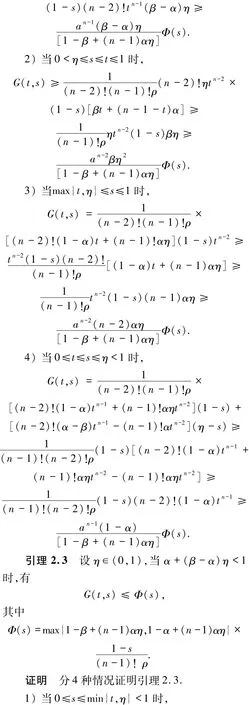
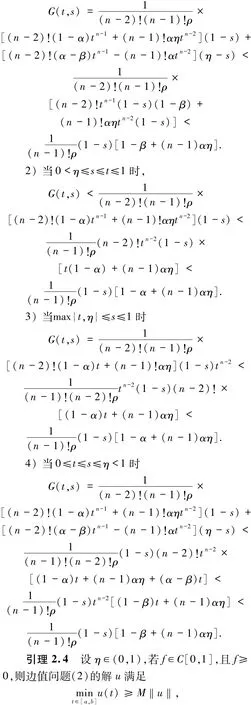

其中
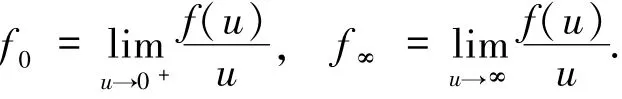
3 第二部分主要結果及證明



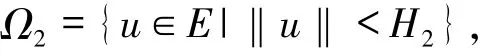
則
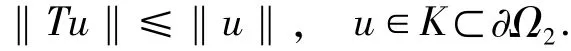
故邊值問題(2)至少有一個正解.
高階微分方程解的研究在實際應用中比較廣泛,便于對實際問題監控和預測,更多深入系統的研究可以參考文獻[3-9].
致謝 西北師范大學知行學院2019年校級科學研究項目(2019002KA)對本文給予了資助,謹致謝意.

