四階熱傳導(dǎo)方程解爆破的一個新條件

熊梓伶， 楊 晗

（西南交通大學(xué) 數(shù)學(xué)學(xué)院，四川 成都611756）

由上面的綜述知道，文獻(xiàn)［1-3］中解的爆破準(zhǔn)則不一樣，文獻(xiàn)［1，3］是考慮解的L2范數(shù)的破裂，文獻(xiàn)［2］則是研究了解的時空范數(shù)的破裂，文獻(xiàn)［4］的爆破條件與文獻(xiàn)［1-3］有所不同，對非線性項的要求文獻(xiàn)［4］的結(jié)論更深刻，它與對應(yīng)的特征值問題有關(guān).基于以上思想，本文主要結(jié)合特征值，利用Galerkin方法和凸性方法，研究方程解的存在性和一類新的爆破條件.

本文主要結(jié)論如下.

定理1 函數(shù)u滿足條件

則對于原方程的解u在有限時間T滿足

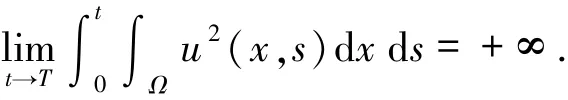
1 局部解的存在性

定理1.1 當(dāng)u0∈H20時，方程組（1）存在局部解u滿足

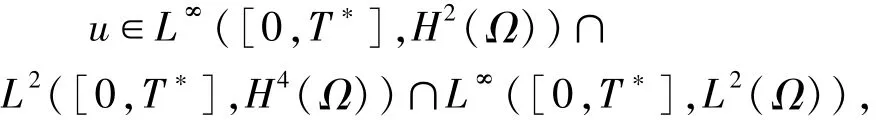
且

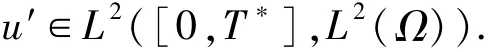
本文利用Galerkin方法證明解的存在性.在H20（Ω）中選擇一組基礎(chǔ)函數(shù)wj（j∈N），wj是滿足以下Dirichlet邊界條件的Laplacian算子的特征函數(shù)

其中‖wj‖L2＝1.

1）構(gòu)造近似解.對給定的正整數(shù)m，記

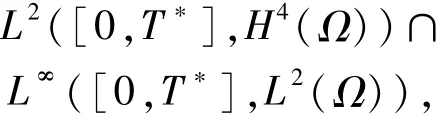
且

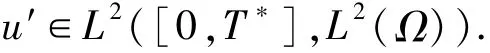
2 主要定理的證明

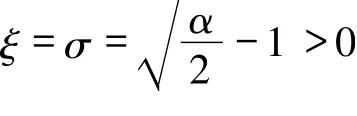
時，可得

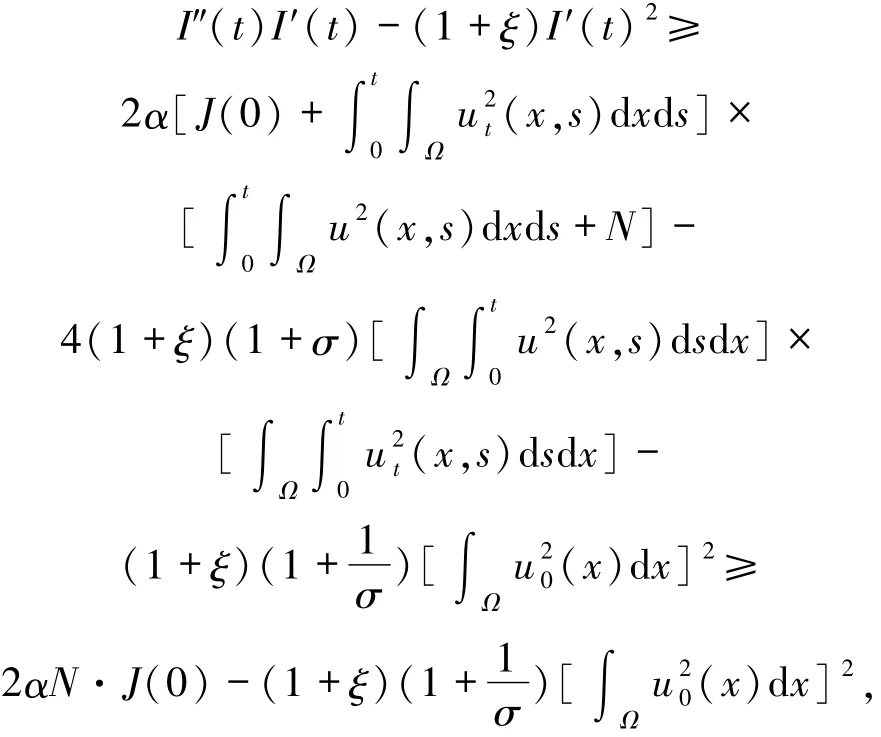
其中

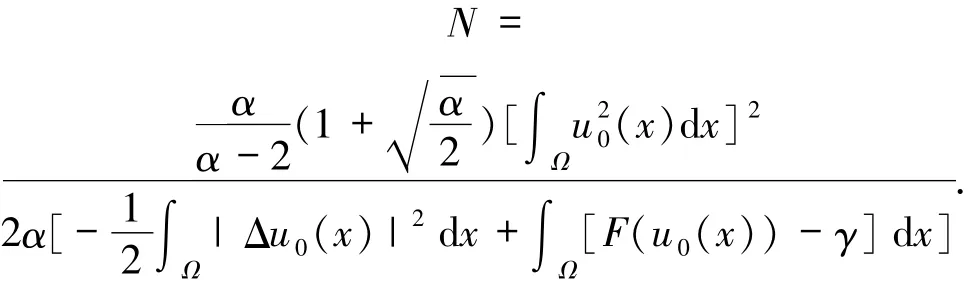
由于J（0）＞0，N＞0，可得

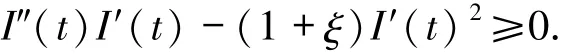
爆破時間T滿足

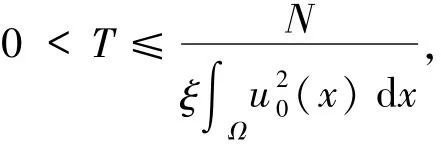
也就是說，當(dāng)t≥0時，解u（x，t）在時間趨于T時爆破.