p階強度量正則性的擾動穩定性

許文丁， 何詣然

（1.四川師范大學 數學科學學院，四川 成都610066； 2.四川旅游學院 旅游文化產業學院，四川 成都610100）

1 引言及預備知識

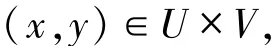
定理1.1稱為Graves定理.若映射f：X→Y在xˉ處嚴格可微，則由嚴格可微（不妨設f在xˉ處的導數為f′（xˉ））的定義可知，對任意ε＞0，存在xˉ的鄰域U，使得對任意x，x′∈U，有

有

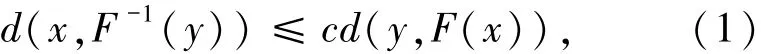
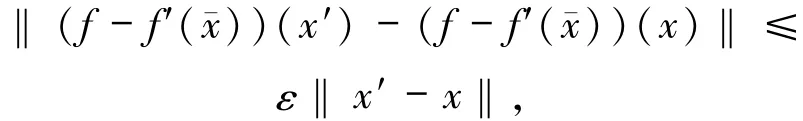
其中記號d（z，A）表示點z到集合A的距離，即

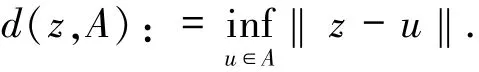
使（1）式成立的所有常數c關于鄰域U×V的下確界稱為F在xˉ處的度量正則模，記為reg F（xˉ｜yˉ）.F在xˉ處度量正則當且僅當reg F（xˉ｜yˉ）＜∞.

眾所周知，對單值映射g：X→Y，常數L≥0，若存在xˉ的鄰域U，使得對任意x，x′∈U，都有

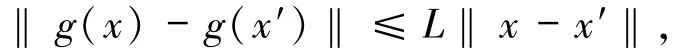
則稱g在xˉ處關于常數L局部Lipschitz連續，常數L關于鄰域U的下確界稱為Lipschitz模，記為Lip（g；xˉ）.

由經典的Banach開映像定理可知，連續線性映射A：X→Y是度量正則的當且僅當它是滿射.對于非線性映射f：X→Y，文獻［1］得到如下結論.

定理1.1 設f：X→Y為映射，A：X→Y為連續線性映射，κ，μ＞0滿足κμ＜1.若以下條件成立：

（i）映射A關于常數κ度量正則；

（ii）映射f-A關于常數μ全局Lipschitz連續；

即映射f-f′（xˉ）在xˉ處是局部Lipschitz連續的，且其Lipschitz常數可以任意小.這樣，由定理1.1便容易證得如下推論.

推論1.1 設映射f：X→Y在xˉ處嚴格可微，若其導數為f′（xˉ）是滿射，則其自身為度量正則的.

事實上，以上推論為充分必要條件，其逆命題的證明可由被稱為“推廣的Lyusternik-Graves定理”（見文獻［2-4］等）所得到.

定理1.2 設κ、μ為2個非負常數滿足κμ＜1，F：XY為集值映射，（xˉ，yˉ）為F的圖像上一點，g：X→Y為在xˉ處局部Lipschitz連續的單值映射.若F在xˉ處度量正則且

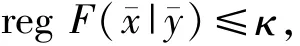
同時有

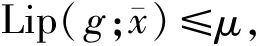
則映射F+g在xˉ處度量正則，且

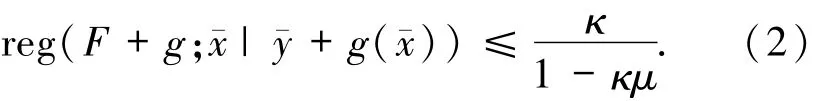
關于強度量正則性，也有以下相應的結論（見文獻［3］等）.

定理1.3 設κ、μ為2個非負常數滿足κμ＜1，F：X Y為集值映射，（xˉ，yˉ）為F的圖像上一點.g：X→Y為在xˉ處局部Lipschizt連續的單值映射.若F在xˉ處強度量正則且reg F（xˉ｜yˉ）≤κ，同時有Lip（g；xˉ）≤μ，則映射F+g在xˉ處強度量正則，且（2）式成立.

定理1.2與定理1.3說明，（強）度量正則的映射經滿足一定條件的Lipschitz映射的擾動后所得映射仍是（強）度量正則的.近幾十年來，定理1.2與定理1.3在不同情形下的推廣形式被學者們廣泛研究和討論，有興趣的讀者可參見文獻［2-9］及其參考文獻.下面介紹有關p階度量正則性的概念及相關結論.

定義1.2 設p＞0為一常數，F：X Y為集值映射，（xˉ，yˉ）為F的圖像上一點.稱映射F在xˉ處p階度量正則，如果存在常數c＞0以及xˉ與yˉ的鄰域U和V，使得對任意（x，y）∈U×V，有

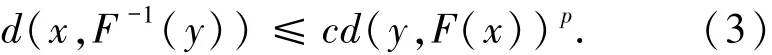
使（3）式成立的所有常數c關于鄰域U×V的下確界稱為F在xˉ處的p階度量正則模，記為regpF（xˉ｜yˉ）.類似地，F在xˉ處p階度量正則當且僅當

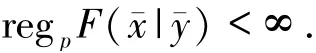
關于p階度量正則性的擾動穩定性，文獻［10］中給出了如下結論（由于本文所涉及的空間均為賦范空間，因此將該結論中的距離空間統一換成賦范空間，距離統一換成范數）.

定理1.4 設X為Banach空間，Y為賦范空間.考慮映射H：＝G+h，其中G：XY為集值映射，h：X→Y為單值映射.設yˉ∈G（xˉ），常數η＞0.假設：

（i）映射G的圖像在（xˉ，yˉ）處是局部閉的；

（ii）存在c，p＞0，使得對任意（x，y）∈B（xˉ，η）×B（yˉ，η），有

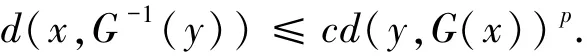
同時，對任意x，x′∈B（xˉ，η），都有

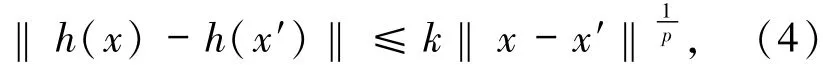
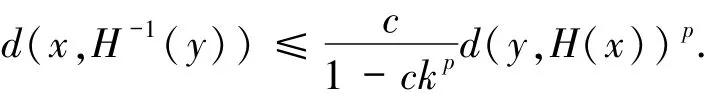
其中k∈（0，c-1p），則存在r＞0，使得滿足（4）式的單值映射h稱為在處階H?lder連續，常數k稱為h在xˉ處的H?lder常數.

定理1.4說明了在一定條件下（度量正則常數與H?lder常數的乘積嚴格小于1），p階度量正則的映射經階H?lder連續的函數擾動后所得函數仍為p階度量正則的.顯然，當p＝1時，定理1.4便退化為定理1.2.

類似于強度量正則性，可以定義如下p階強度量正則性.

定義1.3 設p＞0為一常數，F：X Y為集值映射，（xˉ，yˉ）為F的圖像上一點.稱F在xˉ處p階強度量正則，如果其逆映射F-1在yˉ處存在一個p階H?lder連續的單值局部化，即存在xˉ與yˉ的鄰域U′和V′，使得映射

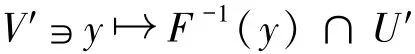
為單值映射且在yˉ處局部p階H?lder連續.

自然要問，關于強度量正則性的經典擾動穩定性結論（定理1.3），是否也有類似于定理1.4的，推廣至p階情形的結論？本文的主要結論回答了上述問題的答案是肯定的.

2 主要結論

為證明本文的主要結論，需要用到關于p階Aubin連續性的概念及相關結論（見文獻［11-12］）.首先，對于集合A、B，記

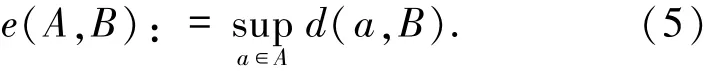
定義2.1 給定常數p＞0，設T：X Y為集值映射，yˉ∈T（xˉ），且T的圖像在（xˉ，yˉ）處局部閉.稱T在xˉ處p階Aubin連續，如果存在常數κ≥0以及xˉ的鄰域U與yˉ的鄰域V，使得對任意x′，x∈U，都有

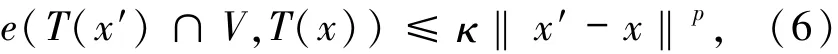
或者，等價地

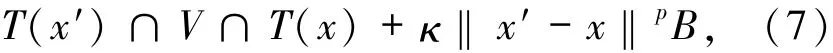
其中B：＝｛y｜‖y‖≤1｝.使得（6）式成立的所有κ關于鄰域U×V的下確界記為Lipp（T；xˉ｜yˉ）.顯然，當映射T取單值時，其在xˉ處的p階Aubin連續性即為p階H?lder連續性.此時，記Lipp（T；xˉ｜T（xˉ））為Lipp（T；xˉ）.

文獻［3］等證明了映射F的度量正則性等價于其逆映射F-1的Aubin連續性.為了證明該等價性可推廣至p階情形［11-12］，首先證明如下引理.

引理2.1 設常數p＞0，點（xˉ，yˉ）在映射T：X Y的圖像上.若T在xˉ處p階Aubin連續，則對于yˉ的任一鄰域V，存在xˉ的鄰域U，使得對任意x∈U，有T（x）∩V≠?.

證明 由映射T在xˉ處的Aubin連續性可知，存在xˉ的鄰域U′與yˉ的鄰域V′，使得對任意x∈U′，有

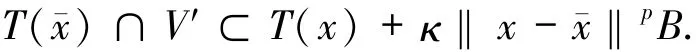
于是，對任意x∈U′，有

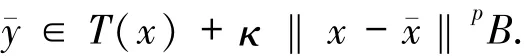
因此，存在y∈T（x），v∈B，使得

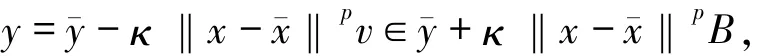
進而有

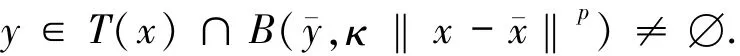
注意到，對于yˉ的任一鄰域V，都存在xˉ的鄰域U，使得U?U′，并且對于任意x∈U，有

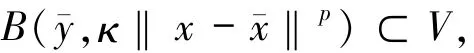
這樣便得到對于任意x∈U，有

引理得證.

對于映射F，其強度量正則性等價于其逆映射F-1具有Aubin連續性且處處不取多值，以下引理說明了該等價性可推廣至p階情形.

引理2.2 設T：X Y為集值映射，yˉ∈T（xˉ），則下列2個命題等價：

（i）T在xˉ周圍存在一個以κ為H?lder常數的p階H?lder連續的單值局部化；

（ii）T在xˉ處關于常數κ是p階Aubin連續的且在xˉ處存在一個不取多值的局部化t：X→Y.

證明 （i）?（ii）是顯然的.下面證明（ii）?（i）.

設T在xˉ處關于常數κ是p階Aubin連續的，則由引理2.1可知t為T在xˉ周圍的一個局部化.因此，存在a，b＞0，使得T（x）∩B（yˉ，b）≠?，并且

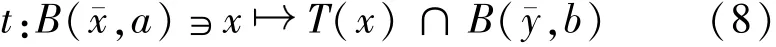
為單值映射.取a′＞0使得

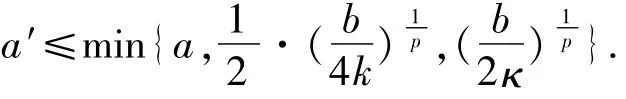
這樣，對任意x，x′∈B（xˉ，a′），都有

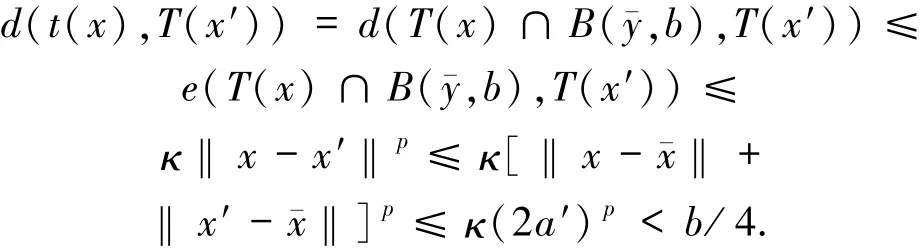
于是，存在y′∈T（x′），使得

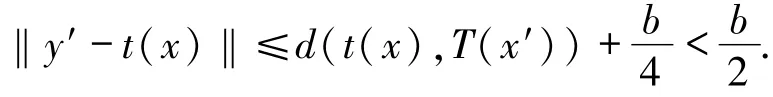
由于映射t取單值，故而由t的構造知

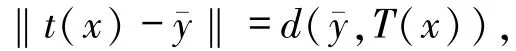
于是得到

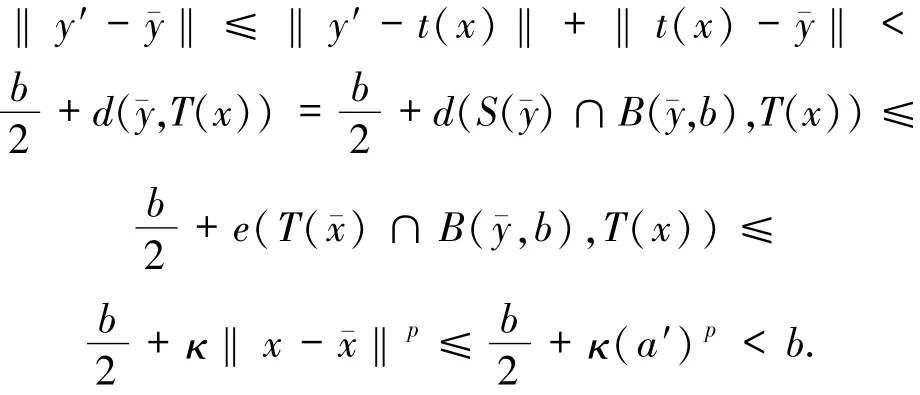
因此，有y′∈B（yˉ，b）.進而

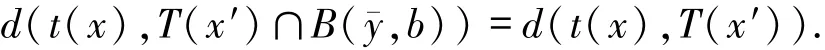
于是可知

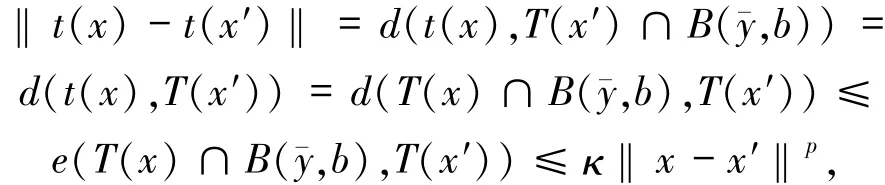
即t為T在xˉ周圍的以κ為常數的p階H?lder連續的單值局部化.引理得證.

此外，類似于1階Aubin連續性，p階Aubin連續性也具有如下性質［3］.

引理2.3 設p＞0為常數，T：XY為集值映射，yˉ∈T（xˉ），且T的圖像在（xˉ，yˉ）處局部閉，則T在xˉ處p階Aubin連續當且僅當存在xˉ的鄰域U及yˉ的鄰域V，使得對任意x′∈X，x∈U，有

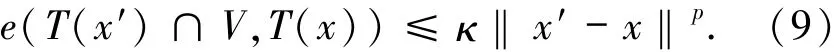
證明 若對任意x′∈X，x∈U都有（9）式成立，則由p階Aubin連續性的定義可知T在xˉ處顯然是p階Aubin連續的.

結合（b）并運用定理1.4，可知映射H＝g+F在xˉ處p階度量正則，且

3 結論

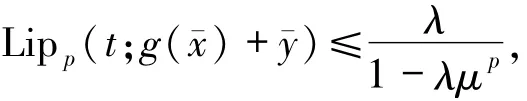
本文的主要結論（定理2.3）給出了關于p階強度量正則性的擾動穩定性結論.該結論指出，p階強度量正則的集值映射在經階H?lder連續的單值映射擾動后，所得到的映射仍然是p階強度量正則的.顯然，當p＝1時，定理2.3便退化為經典結果定理1.3.

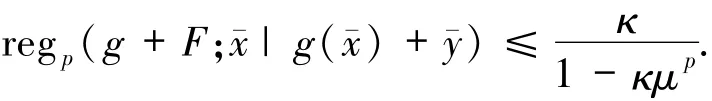
致謝 四川旅游學院2019年度校級科研項目（19SCTUZZ02）對本文給予了資助，謹致謝意.

定理得證.