配對設計中缺乏差值標準差情況下的樣本量估計策略*

南方醫科大學公共衛生學院生物統計學系(510515) 邢 星 吳 瑩 陳平雁

【提 要】 目的 在臨床配對設計試驗中，利用定量指標變化值(干預前后差值)進行兩組比較時，其樣本量的準確估計需要依據兩組變化值的均數和標準差。如果參數假設源于外部數據的話，通常會缺少變化值的標準差信息。本研究旨在探索配對設計中缺乏差值標準差情況下的樣本量估計策略。方法 兩組變化值的均數可直接從干預前均數與干預后均數相減得到。經理論推導，假設兩組方差齊性，變化值的標準差可利用干預前后的相關系數與原數據共同標準差求得。結果 在配對設計中缺少變化值的標準差的情況下，如何準確估計樣本量實質上是一個如何準確估計干預前后測量值的相關系數的問題。如果相關系數高估，則導致檢驗效能偏低，即樣本量相對不足；如果相關系數低估，則導致檢驗效能升高，使得樣本量過大而造成浪費。結論 缺乏差值標準差的配對設計在進行樣本量估計時應借助相關程度來提高樣本量估計的有效性。

在配對設計臨床試驗中，定量指標的干預前后變化值是常見的療效評價指標。對于此類指標兩組比較的樣本量估計，除了需要確定檢驗水準和檢驗效能外，還需設置變化值的均數和標準差參數。如果參數假設源于外部數據(如文獻報道)，通常會缺少變化值的標準差信息，難以準確估計樣本量。本研究旨在探索在配對設計中缺乏差值標準差情況下的樣本量估計策略。

方 法

樣本量的估計原理通常基于檢驗統計量和H1假設進行反推[1-4]。對于定量指標，假設給定模型參數θ的函數f(θ)為效應量指標，T表示f(θ)的無偏估計統計量，測量值服從正態分布且滿足兩組方差齊性，則有

(1)

如采用雙側檢驗，給定檢驗水準α及檢驗效能1-β。

在H0假設下f(θ)=0，α水平下針對H0的檢驗界值為

(2)

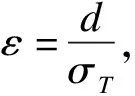
(3)

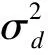
(4)

在兩組方差齊性假設下，令σ2為原數據的共同方差，則有[5]

(5)

其中，ρ為干預前與干預后測量值的總體相關系數。

結 果

臨床實際中，通常0<ρ<1。當ρ=0.5時，σd=σ，此時用σ估計樣本量與理論估計的樣本量一樣；當ρ<0.5時，σd>σ；此時用σ估計樣本量較理論估計的樣本量要大；當ρ>0.5時，σd<σ；此時用σ估計樣本量較理論估計的樣本量要小。因此，在缺少變化值的標準差的情況下，如何準確估計樣本量實質上是一個如何準確估計干預前后測量值的相關系數的問題。如果相關系數高估，則導致檢驗效能偏低，即樣本量相對不足；如果相關系數低估，則導致檢驗效能升高，使得樣本量過大而造成浪費。

設定雙側檢驗水準α為0.05，檢驗效能1-β為90%；兩組變化量之差值的總體均數μd從0.2到0.8，間隔0.1；兩組差值的總體標準差σd相同，均為1.0，即效應量μd/σd從0.2到0.8，間隔0.1。根據公式(4)和公式(5)，計算得到配對設計試驗中不同效應量和相關系數所對應的每組樣本量(表1)。例如，當檢驗效能為0.9、真實的相關系數(總體相關系數)為0.4、效應量為0.5時，正確的樣本量為53。如果計算樣本量時效應量按0.5估計，總體相關系數按0.5估計所求得的樣本量為44，比正確的樣本量低估9例；如果總體相關系數按0.3估計，則樣本量為61，比正確的樣本量高估8例。由表1可見，相關系數每高估或低估0.1，樣本量會相應地低估或高估約10%以上。圖1描述了不同相關系數和效應量所對應的樣本量，可見隨著相關系數增大和/或效應量的增大，樣本量呈減小趨勢。

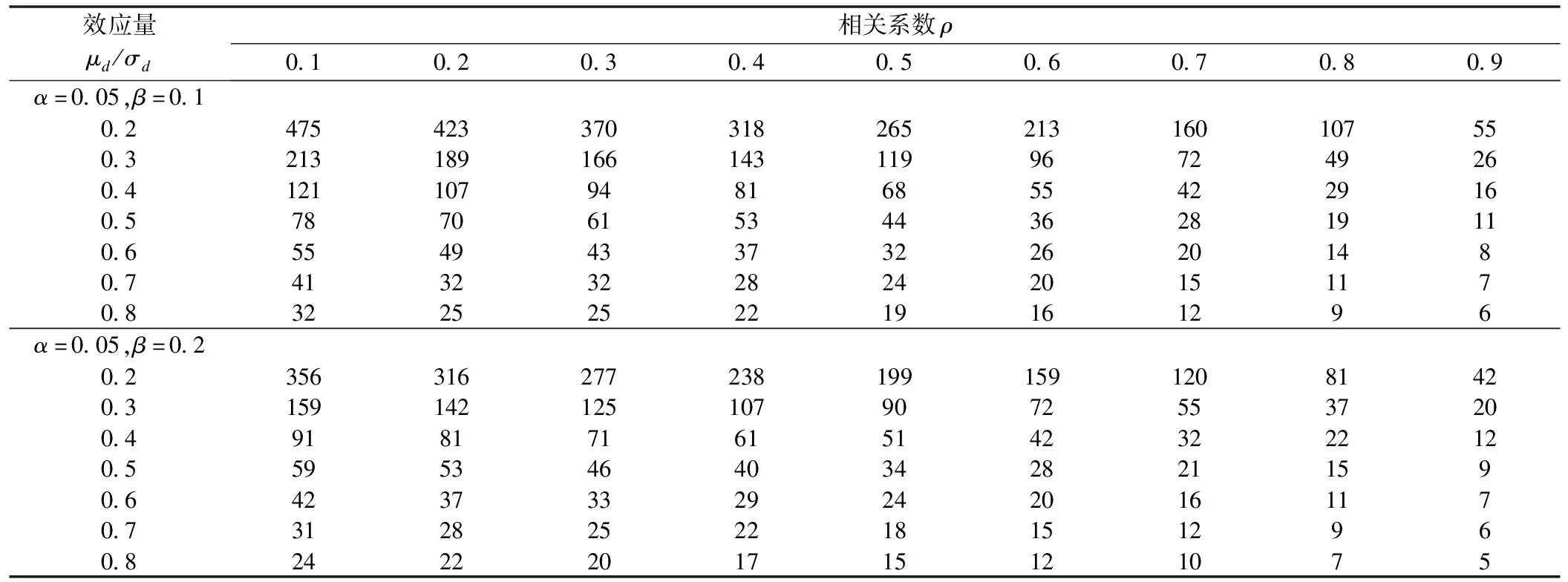
表1 干預前后變量的相關系數和效應量估計對每組樣本量估計的影響

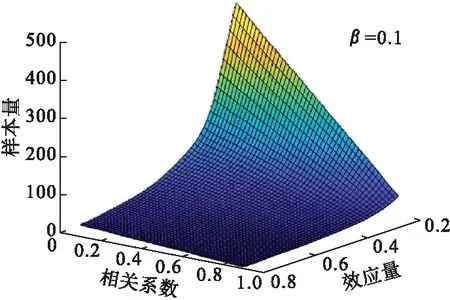
圖1 干預前后變量的不同相關系數和效應量估計的樣本量

討論與結論

本文所提出的策略也適用于定量指標兩組配對設計的樣本量估計。雖然文中列舉了兩組樣本量均衡的情況，在兩組樣本量比例不同時，基于本研究對變化值標準差的估計策略帶入相應樣本量估計公式即可。

對于定量指標兩組比較的臨床試驗設計，在缺少變化值標準差信息的情況下，如果直接利用原始測量值的標準差進行樣本量估計，則其結果將以干預前后相關系數0.5為界呈現檢驗效能不足或效能過高(即浪費樣本量)的問題。

在缺少變化值的標準差的情況下，如何準確估計樣本量實質上是一個如何準確估計干預前后測量值的相關系數的問題。在獲得總體標準差后，研究者可通過估計配對數據間的相關系數，計算較為準確的樣本量估計值。如果相關系數高估，則導致檢驗效能偏低，即樣本量相對不足；如果相關系數低估，則導致檢驗效能升高，使得樣本量過大而造成浪費。