能量狀態法在高速飛行器上的應用
柳青, 楊勝江, 劉越
(1.北京航空航天大學 航空科學與工程學院,北京 100191; 2.北京空天技術研究所,北京 100074; 3.西北工業大學 航天學院,陜西 西安 710072; 4.哈爾濱工業大學 航天學院,黑龍江 哈爾濱 150001)
與傳統的飛行器不同,高超聲速飛行器表現飛行出多任務、多工作模式、大范圍高速機動的特點[1-3]。此外高超聲速飛行器飛行航程較長并且發動機燃油消耗量大,進而增加起飛規模,所以合理設計高超聲速飛行器上升段飛行方案,可以保證飛行器爬升階段的可控性以及合理的油耗規模。
目前,對于高超聲速飛行器飛行軌跡設計的研究主要針對飛行剖面中的爬升段。因為這一階段是保證飛行器順利達到預設巡航點的基礎,并且飛行時間較長、涉及到的約束條件較多。所以,合理設計高超聲速飛行器爬升軌跡可以降低飛行成本和對飛行器各個子系統的要求[4]。針對高超聲速飛行器爬升過程中的不同約束以及性能指標條件,許多學者對爬升軌跡設計與優化進行了研究。采用定動壓來模擬飛行器加速爬升過程,以平衡推力和質量變化之間的關系。將航跡角變化率作為約束條件之一,并基于自身結構與燃料質量之間的等式關系進行軌跡優化以獲得最省燃油軌跡[5-9]。
飛行器的軌跡優化主要包括解析法和數值法兩大類,目前數值法在高超聲速飛行器的軌跡優化問題中有較多的應用[10-12]。高超聲速飛行器通常采用數值算法[13]進行軌跡優化求解,因為在高超聲速飛行器的方程維度較高且模型復雜。能量狀態法通過引入能量,對飛行器的運動學方程進行簡化,減低了對高超聲速飛行器進行軌跡優化時的模型維度和復雜性。David等[14-15]采用能量狀態法對高超聲速飛行器爬升段軌跡進行優化設計。
但是傳統能量狀態法進行軌跡優化設計時僅考慮采用高超聲速飛行器的質點模型,而高超聲速飛行器的機身/發動機耦合設計,使得姿態對軌跡的影響不可忽視。所以,本文考慮了高超聲速飛行器的姿態運動,將速度、高度、軌跡角和質量作為狀態變量,將迎角和舵面作為控制變量,對能量狀態法進行改進。
1 飛行器/發動機一體化模型
1.1 發動機數學模型
由于高超聲速飛行器的水平起降能力,使得其具有高可用率,在軍事和民用上均具有較高實用價值。其常采用渦輪基組合動力(turbine based combined cycle, TBCC)發動機,如圖1所示。TBCC發動機從起飛就處于渦輪模式,在馬赫數為2.5~3內發動機轉換為沖壓發動機模式,然后由亞燃/超燃沖壓發動機驅動加速度到高超聲速。
根據動量定理,發動機的未安裝推力可以寫為:
(1)
(2)
安裝推力為:
T=φα(Ma,h)TSL=φα(θ0)TSL(TR)
(3)
式中:TSL是可用輸出推力與最大推力的無量綱比值;TR是油門開度;α表示發動機工作狀況,它由馬赫數(Ma)、高度(h)決定,可以定義為無量綱溫度θ的函數。
當飛行條件為θ≤TR時,發動機受Πc(隔離室允許動壓)限制;當飛行條件為θ>TR時,發動機受Tt4(燃燒室出口允許溫度)限制。
考慮到上述控制邏輯,可用推力可寫為關于油門開度的分段多項式形式:
(4)
式中δ0是無量綱壓力比:
(5)
由于高超聲速飛行器機身推進一體化的設計,發動機偏置推力也會對飛行姿態產生影響。假設CTx和CTz為飛行器x軸向和z軸向的推力系數。圖2為在30 km處對應的不同飛行馬赫數下的x軸向和z軸向的推力系數隨迎角的變化趨勢。圖3為在Ma=3下不同飛行高度的比沖隨迎角的變化趨勢。
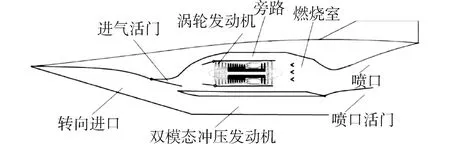
圖1 TBCC推進系統示意Fig.1 TBCC propulsion system schematic
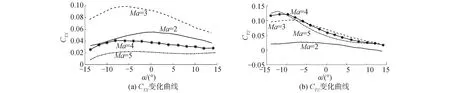
圖2 推力系數Fig.2 Propulsive force coefficients
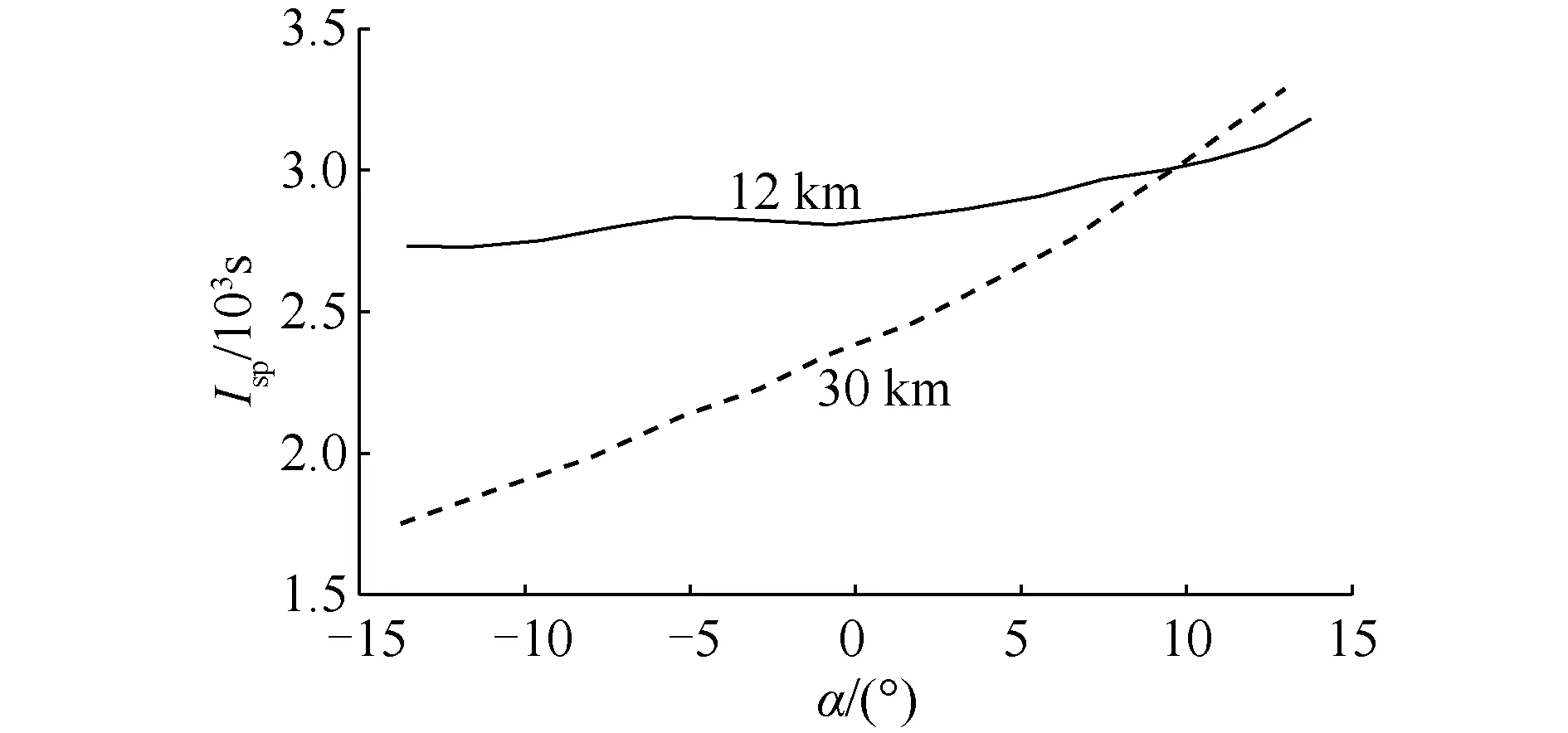
圖3 比沖(Ma=3)Fig.3 Specific impulse(Ma=3)
根據圖2和圖3可知,高超聲速飛行器的發動機推進系統不僅與飛行速度、高度相關,也受飛行迎角的影響。所以在使用能量狀態法對高超聲速飛行器進行分析時,不能僅考慮質點模型。
1.2 氣動數學模型
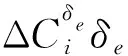
(6)
潔凈體縱向氣動系數的表達式為:
CLclean=(a0+a1Ma)+(a2+a3Ma)α
(7)
(8)
Cmclean=(c0+c1Ma)+(c2+c3Ma)α
(9)
增量縱向氣動系數的表達式為:
(10)
選擇擬合優度(goodness of fit, GOF)和均方根誤差(root mean square error, RMSE)作為模型精確性的評價指標,如表1所示,表明代理模型具有較高的精度。
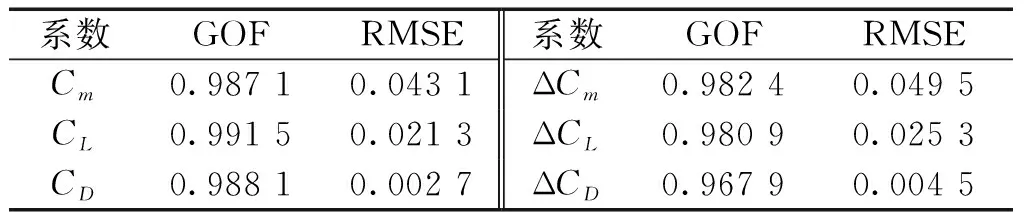
表1 代理模型驗證結果Table 1 Validation results of surrogate models
2 能量狀態法
2.1 方法簡介
對于采用能量狀態法對飛行器進行性能預測,垂直平面上運動的質點模型通常是足夠的。該模型的運動學方程為:
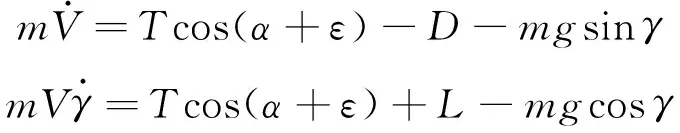
(11)
式中:V為飛行器速度;α為飛行器迎角;γ為軌跡角;ε為推力軸線與零升力軸線之間的夾角;g0為標準重力加速度;Isp為發動機比沖;x、h為地面坐標系中飛機質心的前向和縱向坐標;m為飛機質量。
因為α和ε均較小,所以進行如下簡化:
sin(α+ε)?α+ε,cos(α+ε)?1
(12)
對于在亞音速飛行的飛行器,忽略其飛行姿態進行軌跡設計是足夠的。然而高超聲速飛行器機身推進一體化的設計,發動機的工作情況會受飛行迎角的影響。因此將速度、高度、軌跡角和質量作為狀態變量,將迎角和舵面作為控制變量,采用改進能量狀態法對高超聲速飛行器進行分析。
總能量可以看作是系統連續的狀態變量。定義單位質量飛行器的能量為:
(13)
進而得飛行器質點運動的能量狀態模型:
(14)
2.2 基于能量狀態法的飛行包線分析
能量狀態法假定飛行器縱向剖面由爬升、巡航、下降3種飛行任務階段組成,其能量變化率分別為dE/dt>0、 dE/dt=0和dE/dt<0。所以對于高超聲速的飛行包線對應的是飛行器能量狀態變化率為0的飛行狀態。
基于能量狀態法的飛行包線計算步驟如下:
1)在給定馬赫數下,計算dE/dt=0,則飛行器需要滿足下式的要求:
(15)
在迎角約束(0°<α<8°)和升降舵面約束(|δe|≤20°)的要求下,通過求解式(15),獲得2個高度值,dE/dt=0所對應的高度上界hmaxi和下界hmini。當飛行器的飛行高度在區間[hmaxi,hmini]內時,飛行器的能量變化率大于零,即可以進行爬升/加速運動;
2)計算給定馬赫數范圍內,不同馬赫數下dE/dt=0所對應的高度上下界,得出給定馬赫數范圍內的飛行包線。
根據上述步驟,計算馬赫數在1.2~7的飛行包線范圍,結果如圖4所示。
根據圖4所示的飛行包線結果可以看出發動機由渦輪模態轉換為沖壓模態時會出現一個“推力鴻溝”,會急劇縮小可飛行范圍。高超聲速飛行器在馬赫數為2.5完成從渦輪模態向沖壓模態的轉換。此外,圖5所示推阻關系也與圖4的飛行包線范圍相對應。
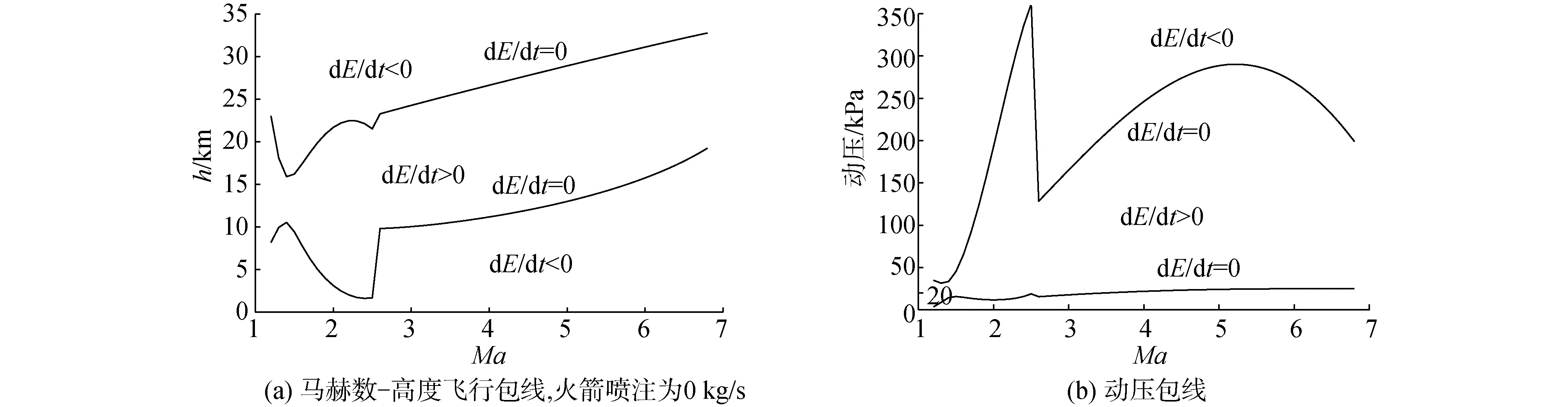
圖4 飛行包線Fig.4 Flight envelope map
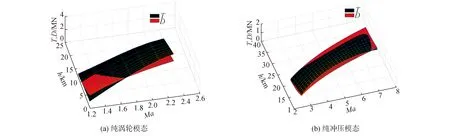
圖5 推阻關系(動壓區間:20~100 kPa)Fig.5 Thrust and resistance relationship map(dynamic pressure area 20~100 kPa)
根據圖5可以得出在馬赫數為1.2~7,飛行器在當前氣動和推進系統狀態下存在可飛行范圍。根據圖5(b)可以看出,沖壓發動機初始的凈推力較小,隨著馬赫數增大沖壓發動機逐漸進入較好的工作狀態。并且高超聲速飛行器在Ma為1.2的超聲速初始飛行階段的可行動壓范圍在5~25 kPa范圍內,可飛行范圍相對較窄,隨著飛行速度增加,飛行包線范圍也逐漸擴展。通過對比圖4和圖5所示的推阻關系,可以看出兩者得出的結論一致。所以,采用能量狀態計算高超聲速飛行器的飛行包線范圍具有一定的可行性。
3 基于能量狀態法的節油軌跡設計
本文對傳統能量狀態法進行改進,以速度、迎角和升降舵偏轉角為控制量,考慮飛行過程中的多約束等條件對高超聲速飛行器的爬升軌跡進行尋優。
3.1 優化模型建立
能量狀態法選取飛機的耗油量為優化性能指標,具體定義為:
(16)
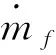
(17)
(18)
對于整個飛行階段,式(17)、(18)可以分解為:
(19)
(20)
式中:下標up、dn表示爬升和下降;VW為風速;λ為巡航飛行中單位距離上的油耗量;dc為巡航里程。此時,軌跡優化問題就轉換為了求解滿足約束(19),使性能指標式(20)最小的優化問題。
3.2 爬升段尋優
總能量E在爬升段是單調增加的,從初始能量E0開始,至末端能量Ef結束,增量為ΔE。采用能量狀態法進行尋優的步驟如下。
1)對每一能量水平Ej,計算最優爬升下的速度、迎角和升降舵偏轉角如下:
(21)
計算相應的飛行高度公式為:
hj=Ej-Vj2/2g
(22)
2)能量水平Ej-1、Ej之間的飛行時間Δtj,軌跡角γj,飛行距離Δdj,以及燃油消耗量ΔFj公式為:
(23)
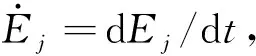
由于爬升段不允許飛機降低高度,故hj≥hj-1,即在能量水平Ej上,高度的最小允許值為hmin,j=hj-1,根據能量方程,這個限制可以轉換為相應的速度上限為:
(24)
為了防止爬升高度超過末端高度hf,高度的最大允許值為hf,其相應的速度下限為:
(25)
除了飛行器的速度約束范圍外,使用能量狀態法尋優的過程中還需滿足如下條件:動壓約束30~100 kPa;高度約束,不允許飛行高度降低;推阻約束(T>D);末端約束。
3.3 爬升軌跡尋優仿真
3.3.1 迎角影響分析
首先采用能量狀態法分析飛行器迎角對最優軌跡和飛行燃油消耗產生的影響。基于改進能量狀態法給出不同迎角下的最省燃油軌跡圖(圖6)以及飛行器質量變化圖(圖7)。
根據圖7和表2中不同迎角下的燃油量可以得知,迎角對發動機的工況和燃油消耗情況影響較大。即使相差較小的迎角,也會產生較大的燃油消耗差異。根據圖6和圖7可以得出,飛行迎角對最優飛行軌跡影響不大,但會對高超聲速飛行器飛行過程中的燃油消耗產生影響很大。
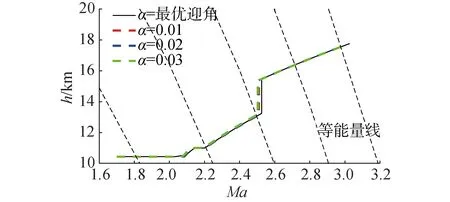
圖6 迎角對軌跡的影響Fig.6 The influence of attack angle on trajectory
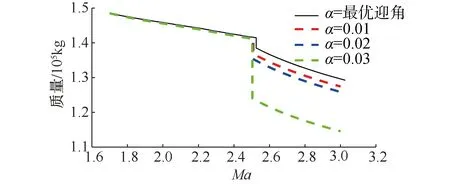
圖7 迎角對燃油消耗的影響Fig.7 The influence of attack angle on fuel consumption

表2 不同迎角下的優化油耗
3.3.2 最優軌跡設計
在此采用改進能量法,考慮飛行過程中的動壓約束、高度約束、推阻約束和末端約束等條件對高超聲速飛行器的爬升軌跡進行優化設計。
采用改進能量狀態法,獲取最優的飛行高度和迎角,進而得到最省燃油軌跡,并且該軌跡滿足飛行過程中的動壓和飛行器舵面物理限制約束。尋優過程設計飛行器從Ma在1.2 ~6.6的最省燃油飛行軌跡。Ma在1.2~6.6,根據上升段尋優過程得到的最省燃油軌跡,如圖8所示。
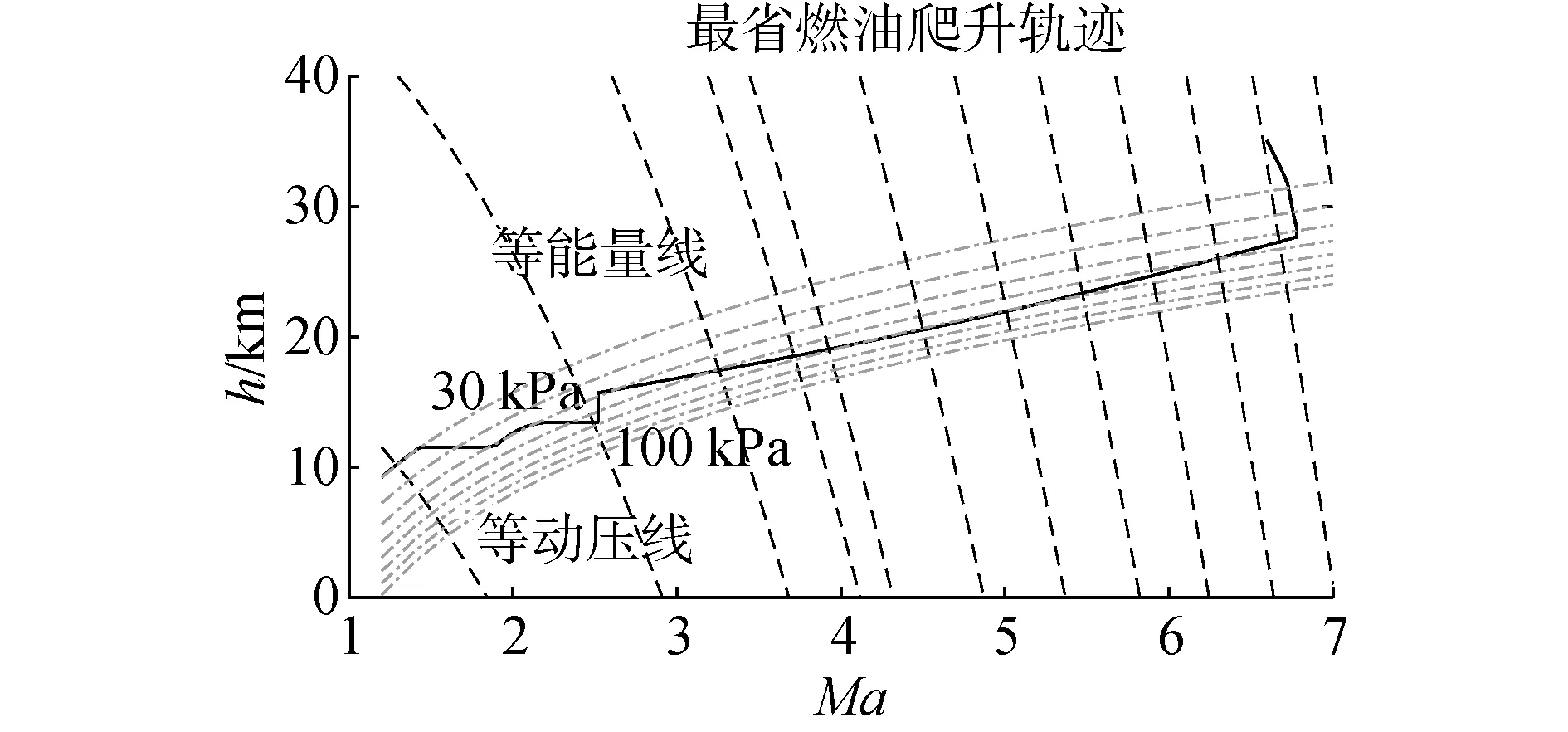
圖8 最省燃油爬升軌跡Fig.8 Minimum-fuel climb trajectory
由能量狀態法獲得的最省燃油爬升軌跡與沿100 kPa等動壓爬升軌跡相比,飛行器沿該軌跡飛行可節省燃油1.87 t。此外,圖8所示的初始時刻沿30 kPa等動壓爬升,與圖5中此時的最大凈推力所對應動壓相吻合。
4 結論
1)采用基于能量狀態法的飛行包線分析,為燃油最省爬升軌跡設計劃定范圍,以避免設計的軌跡在切換至沖壓模態下處于可飛行包線以外。
2)分析迎角對最優軌跡和燃油消耗的影響,以速度、迎角和升降舵偏轉角為控制量,并且考慮飛行過程中的動壓約束、高度約束、推阻約束和末端約束等條件的改進能量狀態法,比常規能量狀態法更適合高超聲速飛行器的爬升軌跡優化設計。

