參數化結構靜態響應特性的減基分析方法

張 正

1.吉首大學信息科學與工程學院，吉首，4160002.吉首大學農礦裝備研發中心，吉首，416000

0 引言

工程實踐中參數化結構的特性分析[1-2]，比如結構響應的靈敏度特性分析[3-4]是一個重要的研究領域。參數化結構的特性分析是建立在參數域與響應集合映射關系之上的，其響應關于參數的靈敏度分析需要計算求解結構響應的有限元向量解。工程中的結構一般較為復雜，離散之后的系統也較為龐大，故而針對結構響應的單次有限元分析耗時較長，尤其對參數域的靈敏度極值這類需要反復多次計算求解結構響應有限元解的問題來說，分析耗時過長，工程上往往難以接受。

結構響應的靈敏度極值分析首先需要分析響應關于參數點的靈敏度計算式，然后在此基礎上將其推廣至全參數域范圍實施遍歷，進而獲得相應的靈敏度極值模型。減基法(RBM)[5-7]能在線高效計算諸多問題的向量解，它在結構響應分析方面計算效率較高，同時在合適的減基空間中計算精度較高[8-10]，故而將減基法直接用于結構響應的靈敏度分析以及靈敏度極值求解等問題具有工程可行性，而這方面的研究工作尚未見諸文獻。

本文研究結構參數域與響應集合之間的減基映射特征，建立結構參數點的靈敏度減基計算式，給出了結構的兩個靈敏度減基極值模型，并通過結構算例進行驗證。

1 減基靈敏度分析

參數化結構靜態響應的有限元平衡方程式為

(1)

式中，μ為結構參數的向量形式;Ω為結構的參數域;m為參數域的維度；K(μ)為結構的參數化剛度矩陣;u(μ)為結構參數化的位移響應向量;F為載荷向量。

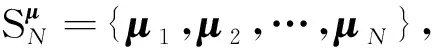
KN(μ)αN(μ)=FN

(2)

(3)

j=1,2,…,p

式中，KN(μ)為結構的N階減基剛度矩陣;FN為與參數無關的N階減基載荷向量;αN(μ)為需求解的N階權系數向量；σj(μ)為受參數影響的標量函數;Kj為結構分離參數獲得的n階剛度矩陣，p為其剛度矩陣分離數目;BN,j、FN分別為不受參數影響的N階矩陣和向量。

綜合減基空間中的基矩陣ZN，可以得到結構在減基空間中的減基位移響應：

uN(μ)=ZNαN(μ)

(4)

離線處理階段將式(3)中的BN,j、FN與ZN予以計算并存儲；在線處理階段則依式(3)、式(2)、式(4)的順序進行調用并計算。

取減基位移響應向量uN(μ)中的一個節點響應作為研究對象，其位移響應記為uN(μ)。在N維減基空間UN中，結構參數向量μ與減基位移響應uN(μ)形成一個連續映射關系：

μuNμ∈Ω

(5)

考慮到結構位移響應隨著結構參數的變化而變化，取參數向量μ的分量，即參數分量μi(i=1,2，…,m)，研究其對結構位移響應的影響，可以得到減基位移響應uN(μ)關于參數分量μi的變化率為

(6)

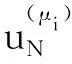
(7)

可以看出，式(7)為減基靈敏度的單步差分形式。由于結構參數向量μ與減基位移響應uN(μ)之間形成的連續映射關系是一個黑箱函數，沒有顯性的表達式，需要利用減基平衡方程式實施點對點的計算，故而減基靈敏度的單步差分式(7)容易造成結構數值計算的奇異性。為了保證結構數值計算的穩定性，需將單步差分形式轉變為兩步差分形式，因此參數化結構的減基靈敏度計算式可變為

(8)

2 減基極值模型

對于參數化結構的分析問題，在全參數域范圍內求解結構節點響應關于參數分量μi(i=1,2,…,m)的靈敏度極值才具有實際的工程意義。由式(8)推導出在結構參數點μ處，節點響應關于參數分量μi的減基靈敏度計算式，如將其在全參數域范圍內遍歷搜尋極值，即可快速獲得參數分量μi的全域靈敏度極值。這是一個減基的工程優化問題。

全參數域上，節點響應關于參數分量μi的靈敏度極值模型的減基形式可表示如下：

(9)

對于減基的工程優化問題(式(9))，只能快速求解節點響應關于參數分量μi的全域靈敏度極值，而不能同時分析全部參數分量的全域靈敏度極值。在全參數域上，同時分析全部參數分量的靈敏度極值是一個工程上的向量優化問題，即多目標優化問題。

綜合式(8)描述的減基靈敏度計算式，節點響應關于全部參數分量的全域靈敏度極值模型的減基形式可表示如下：

(10)

式(10)所示的多目標優化問題沒有具體的工程意義上的優化解，只有Pareto最優解[11]，即會有一個Pareto前沿以供工程上的參考與決策。式(9)和式(10)所描述的兩個工程極值模型由于來源于減基空間下的減基映射關系及其減基列式，因此是兩個具有高效計算特征的工程優化問題，并且它們的離線存儲與在線調用等處理過程與減基法的計算過程是一致的。

3 結構數值算例

研究圖1所示的參數化薄平板結構。l1=0.5 m，l2=0.25 m，厚度為0.02 m，載荷f=380 kN，結構左端為固定端約束。結構的材料參數為彈性模量E(GPa)和泊松比υ，將材料參數記為向量形式μ=(μ1,μ2)T=(E,υ)T∈Ω，其中Ω為結構的參數域(110,220)×(0.15,0.3)，它的維度m=2。將結構用有限元離散成為具有n個自由度(n=3048)的系統，取圖1中節點O處的豎向位移響應進行觀測和研究。在有限元的求解環境下，O點處豎向位移響應關于彈性模量E的靈敏度記為|u(μ1=E)(μ)|，而它關于泊松比υ的靈敏度則記為|u(μ2=υ)(μ)|。該結構算例的數值模擬在MATLAB軟件環境下實施，計算機采用i5-7400CPU、8G內存以及64位操作系統。

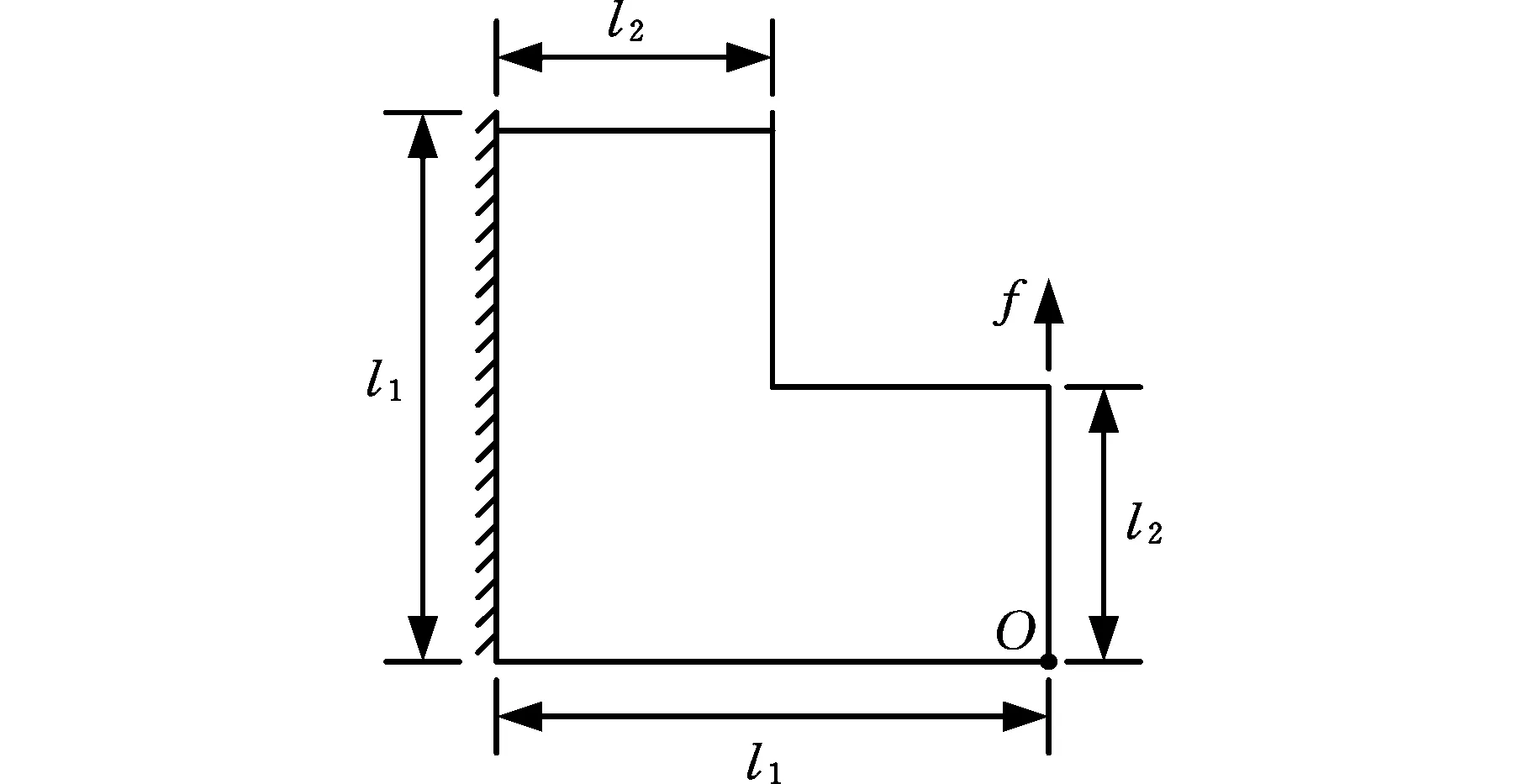
圖1 薄平板結構算例Fig.1 An example of thin plate structure

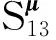
(11)

同樣的過程，依據式(9)獲得利用減基法分析響應關于泊松比υ的靈敏度極值模型：

(12)

類似的過程，依據式(10)獲得同時分析彈性模量E和泊松比υ靈敏度的減基極值模型:

(13)

針對結構算例的靈敏度極值模型(式(11)和式(12))，將數值計算中的有限微元分別選為Δ(μ1)=Δ(E)=1.1×10-3與Δ(μ2)=Δ(υ)=1.5×10-5，并利用遺傳算法[13]進行在線計算。設遺傳算法的種群數為70，最大尋優代數為60，并使其隨機發生器的狀態保持一致。

針對式(11)描述的減基極值模型，利用遺傳算法搜索響應關于彈性模量E的靈敏度極值為2.748 09×10-5m/GPa，其尋優過程如圖2所示。利用遺傳算法結合有限元搜索響應關于彈性模量E的靈敏度極值為2.747 49×10-5m/GPa，其尋優過程如圖3所示。

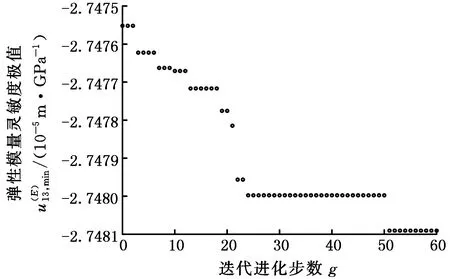
圖2 減基法分析響應彈性模量靈敏度極值Fig.2 The sensitivity extremum of elasticity modulusof response by RBM

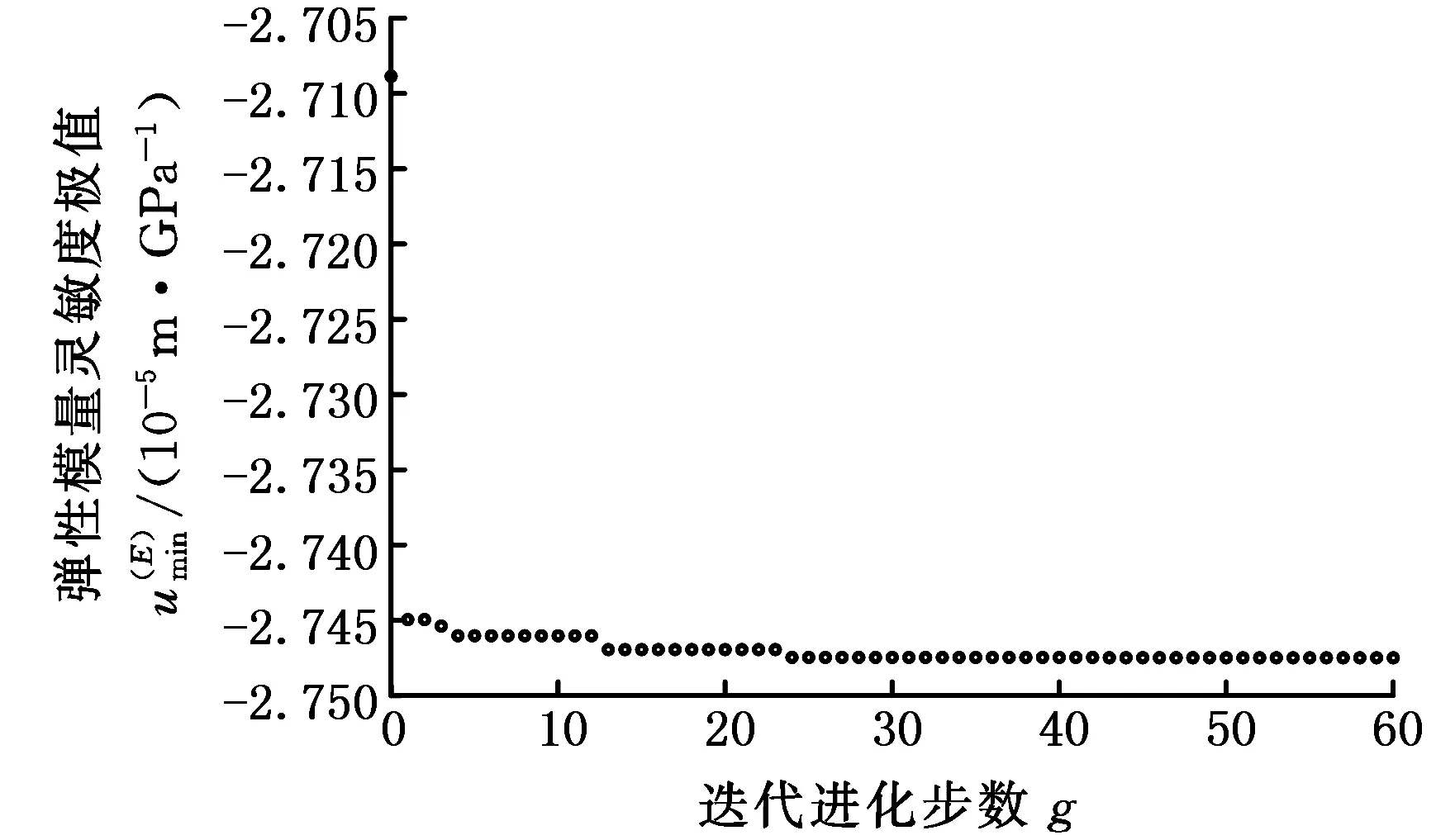
圖3 有限元分析響應彈性模量靈敏度極值Fig.3 The sensitivity extremum of elasticity modulusof response by FE

針對式(12)描述的減基極值模型，利用遺傳算法搜索響應關于泊松比υ的靈敏度極值為0.311 221 mm，其尋優過程如圖4所示。利用遺傳算法結合有限元搜索響應關于泊松比υ的靈敏度極值為0.308 565 mm，其尋優過程如圖5所示。

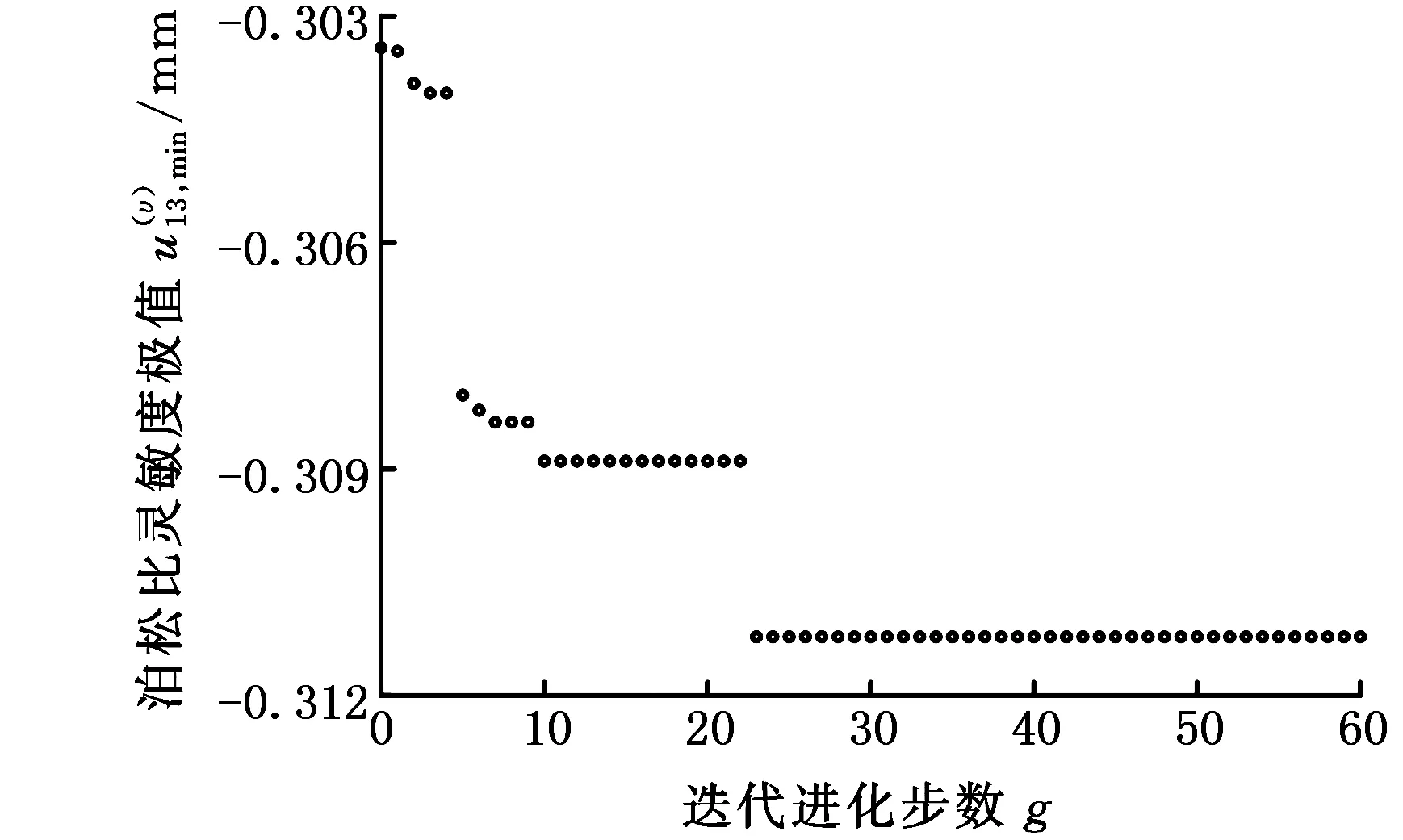
圖4 減基法分析響應泊松比靈敏度極值Fig.4 The sensitivity extremum of Poisson’s ratioof response by RBM

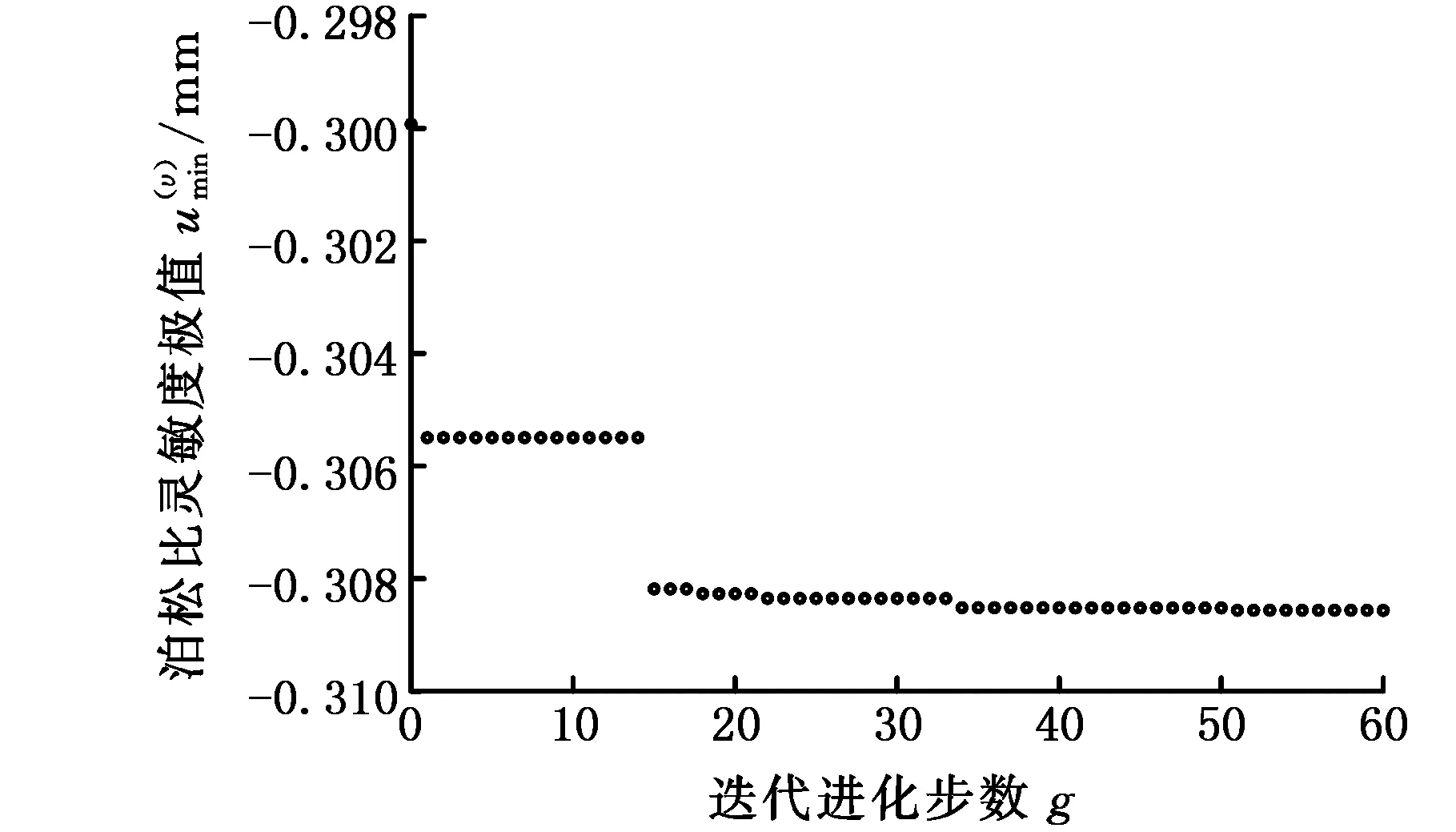
圖5 有限元分析響應泊松比靈敏度極值Fig.5 The sensitivity extremum of Poisson’s ratioof response by FE

將有限元解作為標準解，彈性模量E靈敏度極值的減基算法相對誤差為2.2×10-4，而泊松比υ靈敏度極值的減基算法相對誤差則為8.6×10-3，可以看出，減基法在13維的減基空間中就具有極高的在線計算精確度。另外，同一臺計算機上，利用減基法在線求解彈性模量E和泊松比υ靈敏度極值的計算時間皆約為2.5 s，而采用有限元在線求解彈性模量E和泊松比υ靈敏度極值的計算時間皆約為144.5 s，可以看出，減基法具有相對極佳的在線計算時效性。

針對結構算例的全參數靈敏度極值模型(式(13))，利用多目標遺傳算法[14]進行在線計算。將遺傳算法的種群數量尺寸設置為60，最大尋優代數設置為60，并將其Pareto 前沿的群體比例設置為0.7。針對式(13)描述的減基極值模型，利用遺傳算法尋優獲得的Pareto 前沿如圖6所示。作為比較，利用遺傳算法結合有限元極值模型獲得的Pareto 前沿如圖7所示。由圖6與圖7所示的搜索結果可以看出，利用減基法所獲得的Pareto 前沿與有限元所獲得的Pareto 前沿幾乎是一致的，其中的細微差別是由減基計算中的數值誤差所致。另外，同一臺計算機上，遺傳算法在線求解減基極值模型所耗費的時間約為3.4 s，而遺傳算法在線求解有限元極值模型所花費的時間約為250.5 s，減基法具有相對極佳的計算時效性。

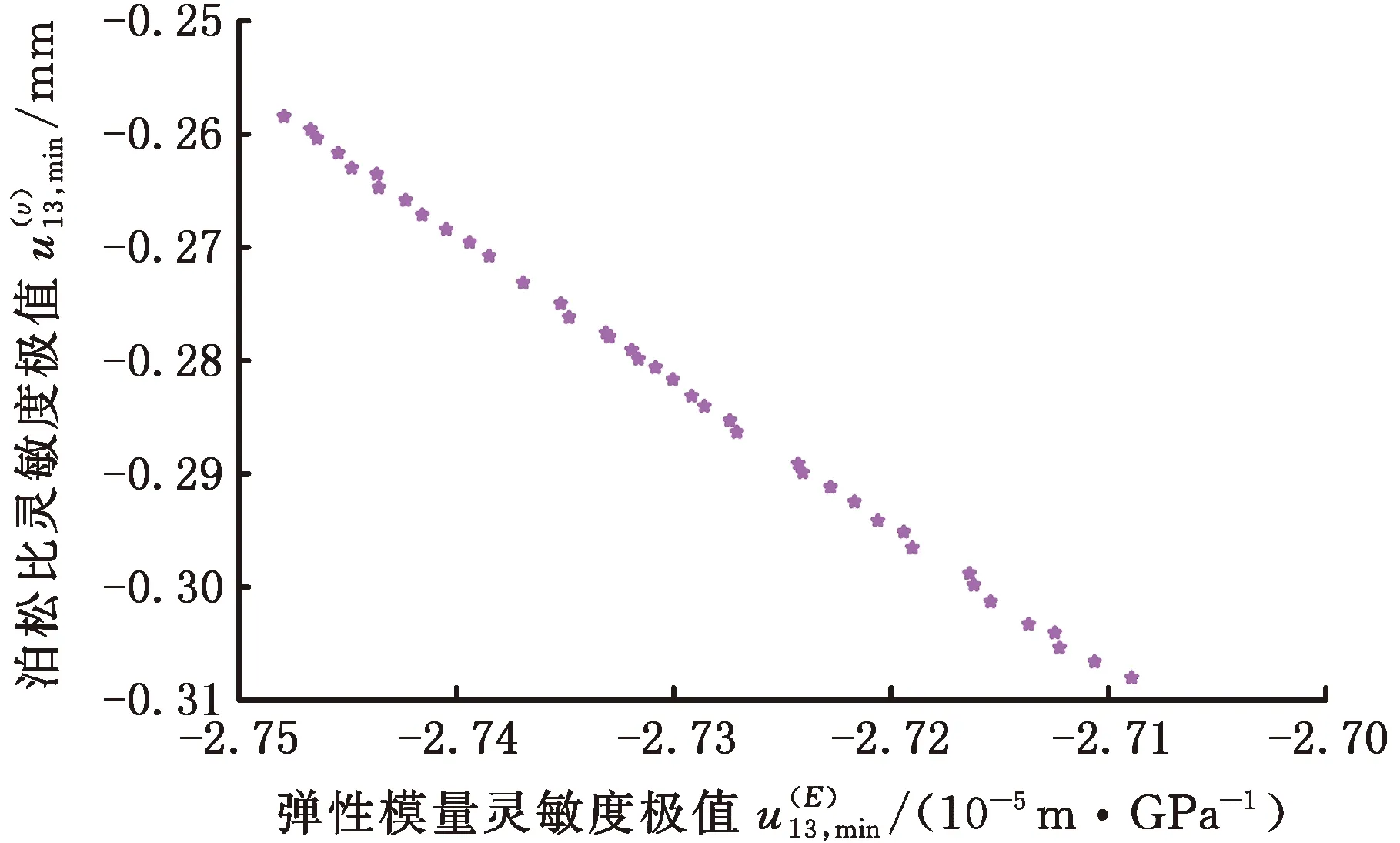
圖6 減基法分析結構響應靈敏度極值的Pareto前沿Fig.6 The Pareto front of sensitivity extremum ofstructural response by RBM

4 結語

本文提出了一種快速分析參數化結構靜態響應特性的減基方法。對于參數化結構,直接利用減基平衡方程作為映射關系進行響應特性分析,同時通過兩步差分法得到了響應關于參數點的靈敏度減基計算式，進而獲得了全參數域范圍上的靈敏度減基極值模型以及全參數的靈敏度減基極值模型。結構算例的數值計算結果表明，相較于有限元法，該方法能夠在確保極高計算精度的條件下獲得極佳的計算效率，具有工程上的可行性和有效性。文中所提的方法為一般性的結構靈敏度分析方法，在具體的工程實踐中可以推廣應用于復雜裝備的響應特性分析工作。