磁軸承激勵下轉(zhuǎn)子系統(tǒng)動力學(xué)特性

李勝遠(yuǎn) 鄭龍席

西北工業(yè)大學(xué)動力與能源學(xué)院，西安，710072

0 引言

高壓壓縮機(jī)轉(zhuǎn)子系統(tǒng)的穩(wěn)定性主要受到油膜軸承和密封動力學(xué)參數(shù)的影響[1]。高密度工作介質(zhì)和高轉(zhuǎn)速使密封的交叉剛度系數(shù)顯著增大，因此轉(zhuǎn)子系統(tǒng)的穩(wěn)定性評價(jià)在高壓壓縮機(jī)的研制中具有重要意義[2-3]。

在API 617標(biāo)準(zhǔn)[4]中，使用一階正進(jìn)動模態(tài)的對數(shù)衰減率來評價(jià)壓縮機(jī)轉(zhuǎn)子系統(tǒng)的穩(wěn)定性。使用磁軸承在軸端進(jìn)行掃頻激勵進(jìn)而獲得對數(shù)衰減率的方法在高壓壓縮機(jī)轉(zhuǎn)子系統(tǒng)的穩(wěn)定性評估中應(yīng)用廣泛。磁軸承主要由電磁鐵、控制器、傳感器和功率放大器組成，通過電磁鐵線圈中的電流產(chǎn)生可控電磁力。相比于傳統(tǒng)的機(jī)械軸承，磁軸承具有無接觸、低機(jī)械磨損、噪聲小和壽命長等優(yōu)點(diǎn)[5]。BAUMANN[6]在額定轉(zhuǎn)速下應(yīng)用磁軸承對轉(zhuǎn)子系統(tǒng)施加了單向簡諧掃頻激勵力，發(fā)現(xiàn)轉(zhuǎn)子系統(tǒng)的反進(jìn)動和正進(jìn)動模態(tài)均被激發(fā)。TAKAHASHI等[7]也采用通過磁軸承施加單向簡諧掃頻激勵力的方法，并應(yīng)用單向頻率響應(yīng)函數(shù)在頻域內(nèi)識別了轉(zhuǎn)子系統(tǒng)一階正進(jìn)動模態(tài)的對數(shù)衰減率。MOORE等[8-9]通過磁軸承對轉(zhuǎn)子系統(tǒng)施加了僅激發(fā)正進(jìn)動模態(tài)的激勵力，并評估了高壓壓縮機(jī)轉(zhuǎn)子系統(tǒng)的穩(wěn)定性裕度。BIDAUT等[10]利用磁軸承在兩個正交方向上分別施加簡諧掃頻激勵力，并通過控制兩個激勵力之間的相位差激發(fā)了轉(zhuǎn)子系統(tǒng)的反進(jìn)動或正進(jìn)動模態(tài)。SOROKES等[11]、SOULAS等[12]和PETTINATO等[13]也分別應(yīng)用磁軸承激勵的方法測試了高壓壓縮機(jī)轉(zhuǎn)子系統(tǒng)的穩(wěn)定性。由上述文獻(xiàn)可知，在不同類型磁軸承激勵力的作用下，轉(zhuǎn)子系統(tǒng)的反進(jìn)動和(或)正進(jìn)動模態(tài)被激發(fā)。然而，從目前公開發(fā)表的文獻(xiàn)看，對磁軸承激勵下轉(zhuǎn)子系統(tǒng)動力學(xué)特性的詳細(xì)分析較少。

為分析磁軸承激勵下轉(zhuǎn)子系統(tǒng)的振動機(jī)理，本文應(yīng)用一維有限元方法建立雙盤轉(zhuǎn)子系統(tǒng)動力學(xué)特性計(jì)算模型，研究在不同類型磁軸承激勵下轉(zhuǎn)子系統(tǒng)的動力學(xué)行為。

1 轉(zhuǎn)子系統(tǒng)有限元建模

1.1 轉(zhuǎn)子軸段的有限元離散

本文采用一維有限元方法對轉(zhuǎn)子系統(tǒng)動力學(xué)建模，采用Timoshenko梁單元以考慮軸段轉(zhuǎn)動慣量和剪切變形的影響。僅考慮轉(zhuǎn)子系統(tǒng)的彎曲振動，轉(zhuǎn)子軸的有限元離散如圖1所示。其中OZ軸為轉(zhuǎn)子系統(tǒng)的旋轉(zhuǎn)軸，第i個轉(zhuǎn)子軸段的廣義坐標(biāo)向量為qi=(uivi,θX,i,θY,i,ui+1vi+1,θX,i+1,θY,i+1)T，(ui,vi)和(θX,i,θY,i)分別為第i個節(jié)點(diǎn)沿X軸和Y軸的橫向位移和轉(zhuǎn)角。轉(zhuǎn)子軸段的局部單元矩陣可由Lagrange方程獲得[14-15]：

(1)

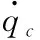
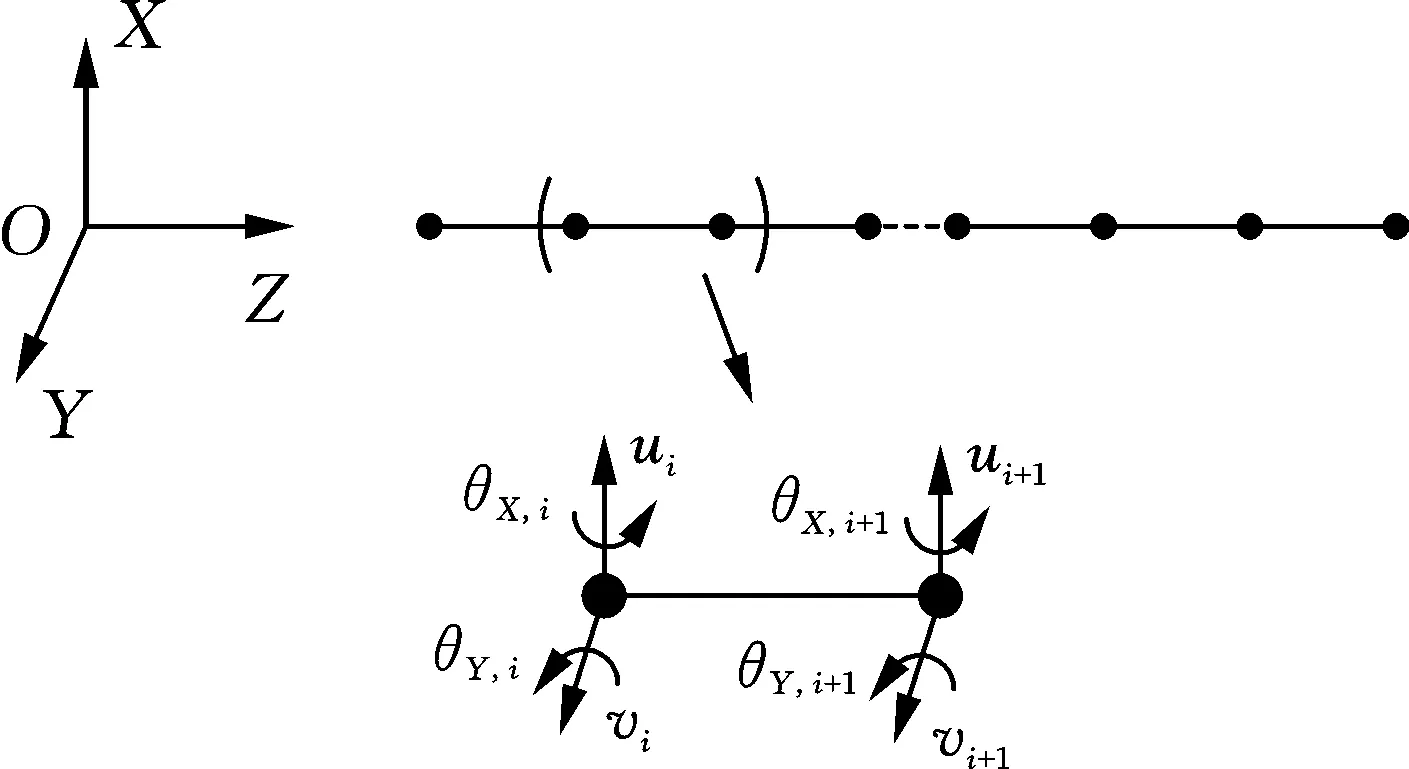
圖1 轉(zhuǎn)子軸的有限元離散Fig.1 Finite element discretization of rotor shaft

分別將T和U代入式(1)可得軸段單元的質(zhì)量矩陣、陀螺矩陣和剛度矩陣。假設(shè)圓盤為剛性盤，忽略其應(yīng)變能，將圓盤的動能代入式(1)可得圓盤的質(zhì)量矩陣和陀螺矩陣。對于支承軸承，假設(shè)其具有線性的載荷變形關(guān)系，由于軸承主要承受徑向載荷，所以只考慮橫向的剛度和阻尼系數(shù)。軸承作用在轉(zhuǎn)子系統(tǒng)上的載荷可寫為軸承處轉(zhuǎn)子位移和速度的函數(shù)[16-17]：

(2)

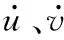
1.2 磁軸承激勵下轉(zhuǎn)子系統(tǒng)動力學(xué)響應(yīng)

轉(zhuǎn)子系統(tǒng)的運(yùn)動微分方程為[18-19]：

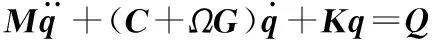
(3)

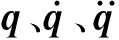
若通過磁軸承在轉(zhuǎn)子系統(tǒng)的l節(jié)點(diǎn)處施加不平衡力形式的激勵力，則該激勵力與轉(zhuǎn)子同向旋轉(zhuǎn)，且在4l-3、4l-2、4l-1、4l自由度處激勵力的分量Q1為[20]

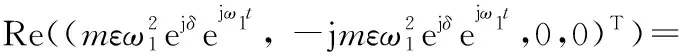
(4)

式中,m為不平衡質(zhì)量;ε為偏心距;δ為相對于X軸正方向不平衡量的相位;ω1為該激勵力的角速度。

若在l節(jié)點(diǎn)處施加角速度為ω2的反向旋轉(zhuǎn)激勵力，則激勵力向量Q2為

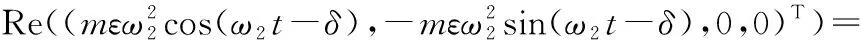
(5)

若通過磁軸承在l節(jié)點(diǎn)的X和Y方向上作用角速度為ω3的簡諧激勵力，則激勵力向量Q3為

Q3=(rcos(ω3t),scos(ω3t+α),0,0)T=
Re((rejω3t,sejω3tejα,0,0)T)=Re(ejω3t(r,sejα,0,0)T)

(6)

式中,r、s分別為X和Y方向上激勵力的大小；α為X、Y兩個方向上激勵力的相位差。

根據(jù)式(4)～式(6)中激勵力的形式，設(shè)作用在轉(zhuǎn)子系統(tǒng)上激勵力和響應(yīng)的形式分別為Qi=Re(Q0ejωit)和qi=Re(q0ejωit)，i=1,2,3，Q0為X和Y方向上激勵力的大小和初相位，q0為復(fù)數(shù)。將Qi和qi代入式(3)可得

(7)

設(shè)復(fù)數(shù)q0的表達(dá)式為

q0=a+bj=|q0|ejβ

(8)

對于激勵力向量Qi，轉(zhuǎn)子系統(tǒng)的響應(yīng)qi為

qi=Re(|q0|ej(ωit+β))=|q0|cos(ωit+β)

(9)

由式(9)可知，復(fù)數(shù)q0的模|q0|為磁軸承激勵下轉(zhuǎn)子系統(tǒng)各個自由度的響應(yīng)幅值；相位β為各個自由度的響應(yīng)相位。

2 轉(zhuǎn)子系統(tǒng)計(jì)算模型

本文研究的雙盤轉(zhuǎn)子系統(tǒng)及軸段的有限元離散模型如圖2所示。轉(zhuǎn)子總長為1.2 m，相鄰節(jié)點(diǎn)間的間隔為0.2 m，轉(zhuǎn)軸直徑為40 mm，轉(zhuǎn)速為3000 r/min。軸承支承在轉(zhuǎn)子兩端，兩個軸承的直接剛度系數(shù)kuu和kvv均為1 MN/m，直接阻尼系數(shù)cuu和cvv均為100 N·s/m，交叉剛度系數(shù)kuv和kvu以及交叉阻尼系數(shù)cuv和cvu均為零。以左端軸承為0位置，圓盤D1和D2分別位于0.4 m和0.8 m處。圓盤的厚度為50 mm，圓盤D1和D2的直徑分別為300 mm和200 mm。轉(zhuǎn)軸和圓盤材料的彈性模量E=211 GPa，剪切模量G=81.2 GPa，密度ρ=7810 kg/m3。

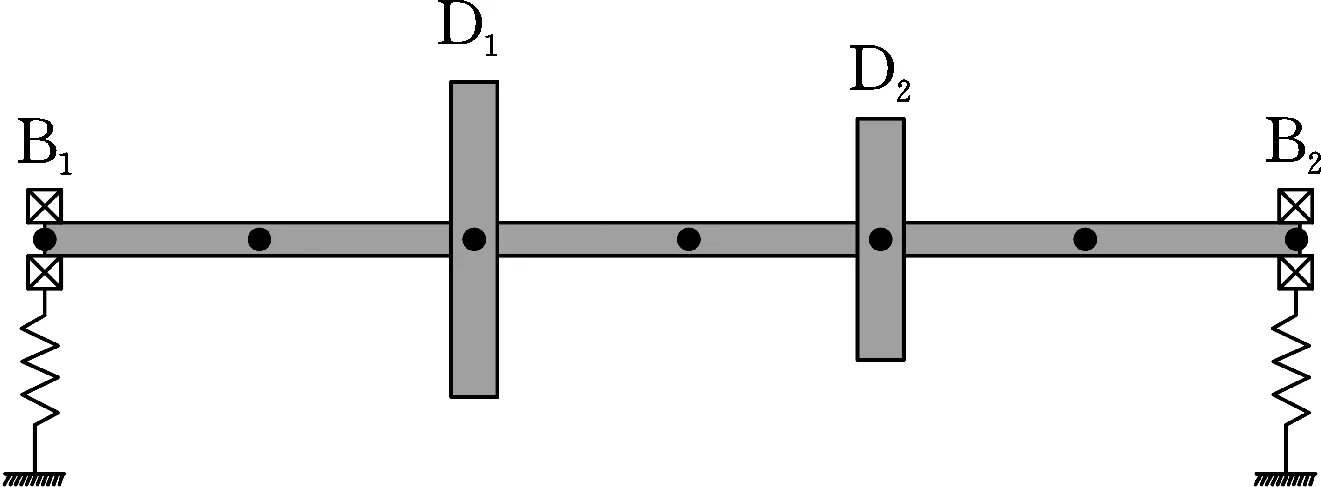
圖2 雙盤轉(zhuǎn)子系統(tǒng)計(jì)算模型Fig.2 Calculation model of a double-disk rotor system

3 計(jì)算結(jié)果

3.1 轉(zhuǎn)子系統(tǒng)固有頻率和模態(tài)振型分析

圖3為該轉(zhuǎn)子系統(tǒng)的Campbell圖。當(dāng)轉(zhuǎn)子轉(zhuǎn)速為3000 r/min時，轉(zhuǎn)子系統(tǒng)的前兩階反進(jìn)動固有頻率分別為18.51 Hz和58.87 Hz，前兩階正進(jìn)動固有頻率分別為18.84 Hz和65.27 Hz。從圖3中可以看出，由于陀螺矩陣的作用，隨著轉(zhuǎn)速的增大，正進(jìn)動固有頻率逐漸增大，反進(jìn)動固有頻率逐漸減小，所以同階反進(jìn)動/正進(jìn)動固有頻率線隨著轉(zhuǎn)速的增大有相互分離的趨勢。

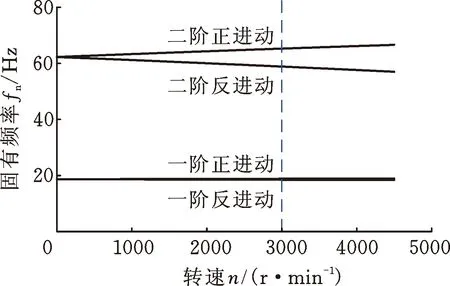
圖3 轉(zhuǎn)子系統(tǒng)的Campbell圖Fig.3 Campbell diagram of the rotor system

由于同階反進(jìn)動/正進(jìn)動固有頻率較為接近，因此同階反進(jìn)動/正進(jìn)動的模態(tài)振型相似。圖4顯示了當(dāng)轉(zhuǎn)速為3000 r/min時，轉(zhuǎn)子系統(tǒng)的前兩階正進(jìn)動模態(tài)振型。對于一階反進(jìn)動/正進(jìn)動模態(tài)振型，轉(zhuǎn)軸進(jìn)動軌道呈U形，兩個圓盤的變形方向相同；而對于二階反進(jìn)動/正進(jìn)動模態(tài)振型，轉(zhuǎn)軸進(jìn)動軌道呈S形，兩個圓盤的變形方向始終相反。

(a) 一階正進(jìn)動模態(tài)振型(fn=18.84 Hz)

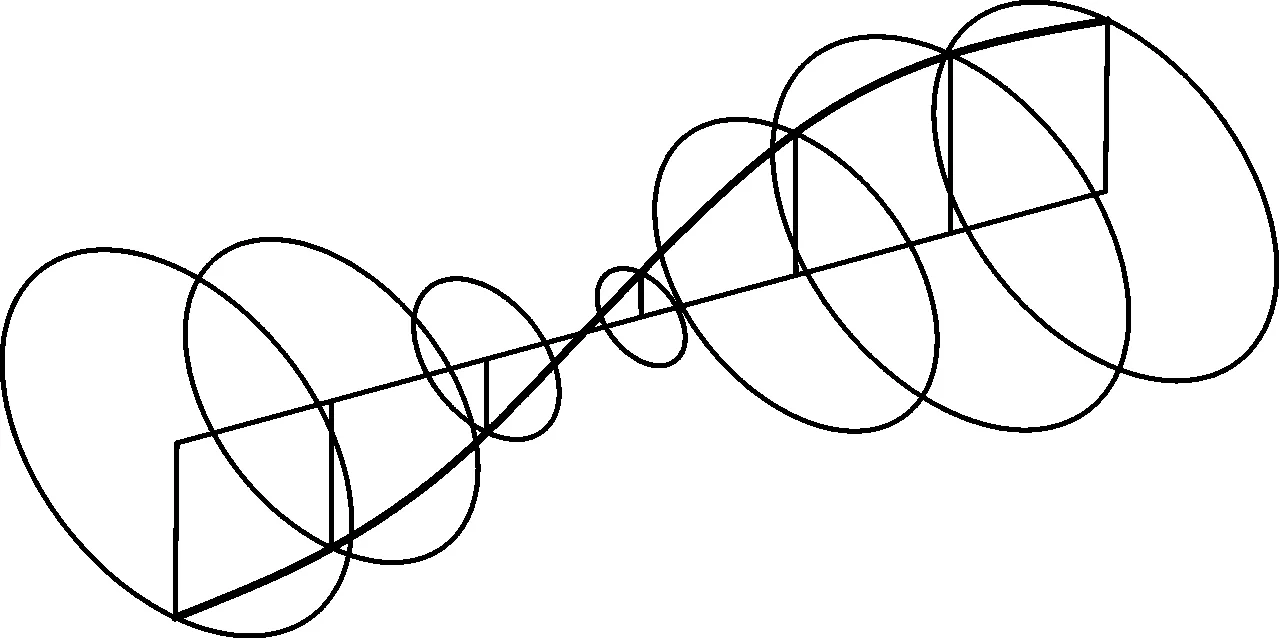
(b) 二階正進(jìn)動模態(tài)振型(fn=65.27 Hz)圖4 轉(zhuǎn)速為3000 r/min時，轉(zhuǎn)子系統(tǒng)的前二階正進(jìn)動模態(tài)振型Fig.4 First two forward mode shapes of the rotor system when the spin speed is 3000 r/min

3.2 同向/反向旋轉(zhuǎn)激勵下轉(zhuǎn)子系統(tǒng)動力學(xué)響應(yīng)

當(dāng)轉(zhuǎn)子轉(zhuǎn)速為3000 r/min，通過磁軸承在轉(zhuǎn)子跨中位置處施加由100 g·mm、0°相位的不平衡量引起的同向旋轉(zhuǎn)激勵力時，圓盤D1和D2的響應(yīng)幅值如圖5所示。從圖中可以看出，在所研究的激勵頻率范圍內(nèi)，圓盤響應(yīng)中出現(xiàn)了兩個響應(yīng)峰值，與圖3比較可知，響應(yīng)峰值對應(yīng)的頻率等于轉(zhuǎn)速為3000 r/min時轉(zhuǎn)子系統(tǒng)的前兩階正進(jìn)動固有頻率，因此，同向旋轉(zhuǎn)的掃頻激勵力激發(fā)了轉(zhuǎn)子系統(tǒng)的正進(jìn)動模態(tài)。

圖6顯示了在響應(yīng)峰值處圓盤的進(jìn)動狀態(tài)，其中“×”表示軌跡起點(diǎn)，“◇”表示軌跡終點(diǎn)，逆時針表示正進(jìn)動，順時針表示反進(jìn)動。從圖6可以看出，在兩個響應(yīng)峰值處，圓盤均為正進(jìn)動，且進(jìn)動軌跡為圓形。在一階正進(jìn)動固有頻率處兩個圓盤的進(jìn)動相位相同，而在二階正進(jìn)動固有頻率處兩個圓盤的進(jìn)動相位相反，這與圖4是一致的。

當(dāng)通過磁軸承在轉(zhuǎn)子跨中位置處施加反向旋轉(zhuǎn)的激勵力時，在不同的激勵頻率下，兩個圓盤的響應(yīng)幅值如圖7所示。與圖3比較可知，圓盤響應(yīng)峰值對應(yīng)的頻率等于轉(zhuǎn)速為3000 r/min時轉(zhuǎn)子系統(tǒng)的前兩階反進(jìn)動固有頻率。圖8顯示了在響應(yīng)峰值處兩個圓盤的進(jìn)動狀態(tài)，可以看出，兩個圓盤均為反進(jìn)動，且進(jìn)動軌跡為圓形，因此，反向旋轉(zhuǎn)的掃頻激勵力激發(fā)了轉(zhuǎn)子系統(tǒng)的反進(jìn)動模態(tài)。當(dāng)轉(zhuǎn)子系統(tǒng)反進(jìn)動時，由于轉(zhuǎn)軸的纖維在進(jìn)動過程中處于拉伸和壓縮的交變狀態(tài)，可能會導(dǎo)致轉(zhuǎn)軸的高周疲勞以及由軸材料內(nèi)阻引起的轉(zhuǎn)子失穩(wěn)，故工程應(yīng)用中應(yīng)避免轉(zhuǎn)子系統(tǒng)出現(xiàn)反進(jìn)動。

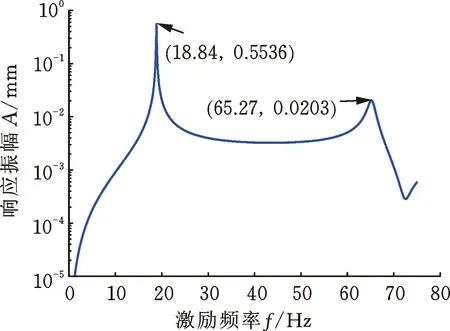
(a) 圓盤D1的響應(yīng)振幅

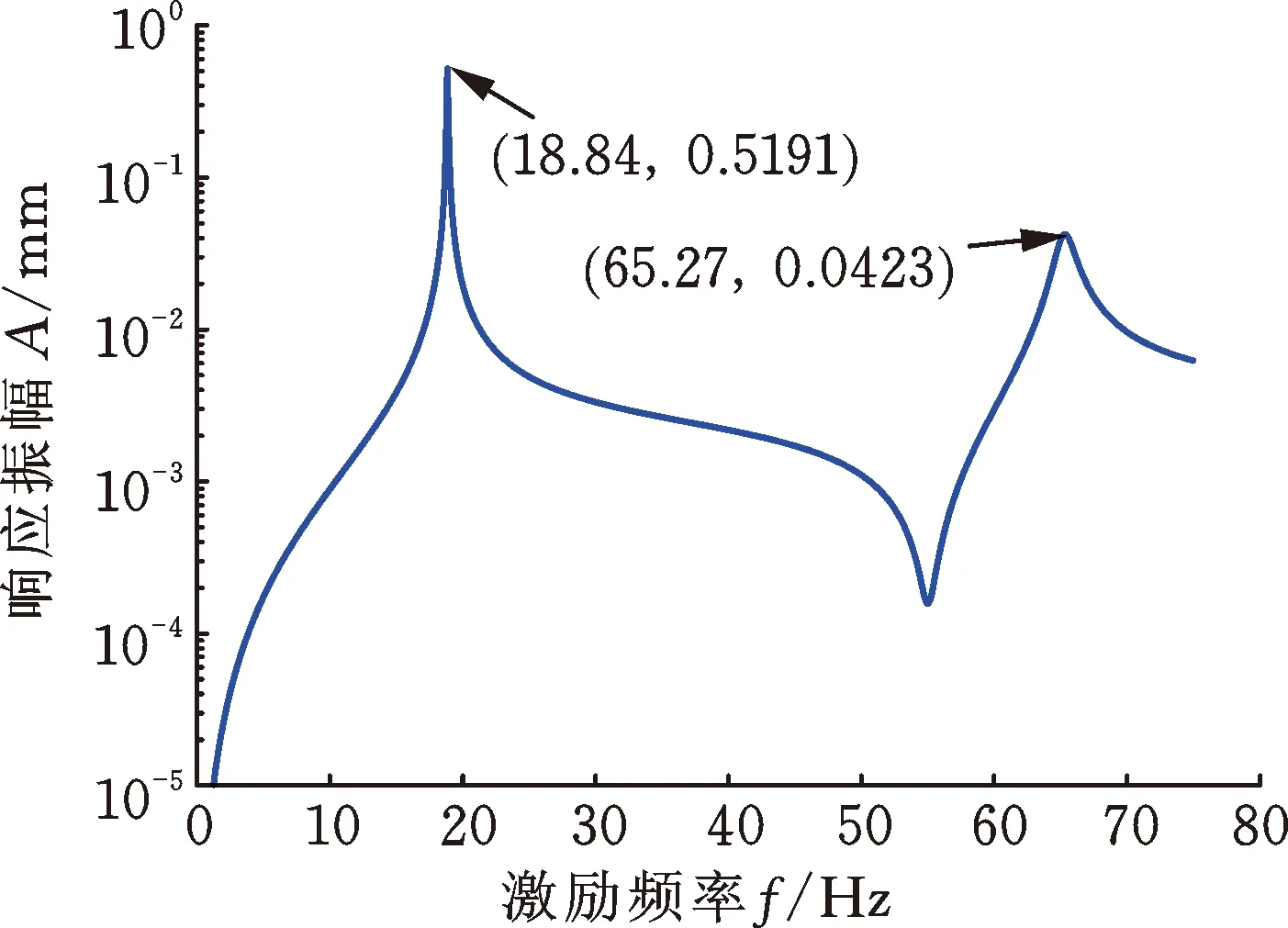
(b) 圓盤D2的響應(yīng)振幅圖5 同向旋轉(zhuǎn)掃頻激勵力下圓盤的響應(yīng)Fig.5 Disks response under co-rotating sweep exciting force

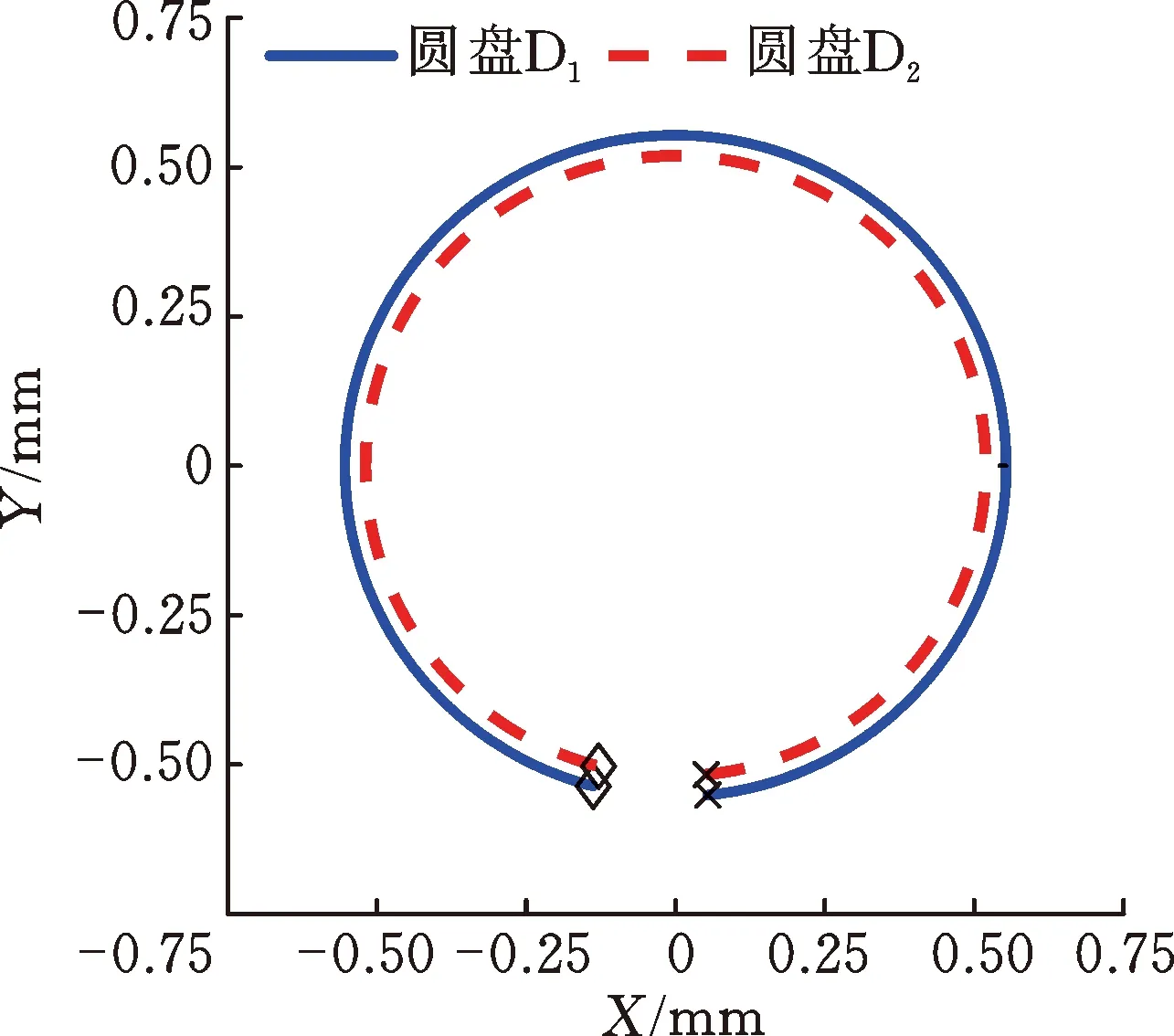
(a) 一階正進(jìn)動固有頻率

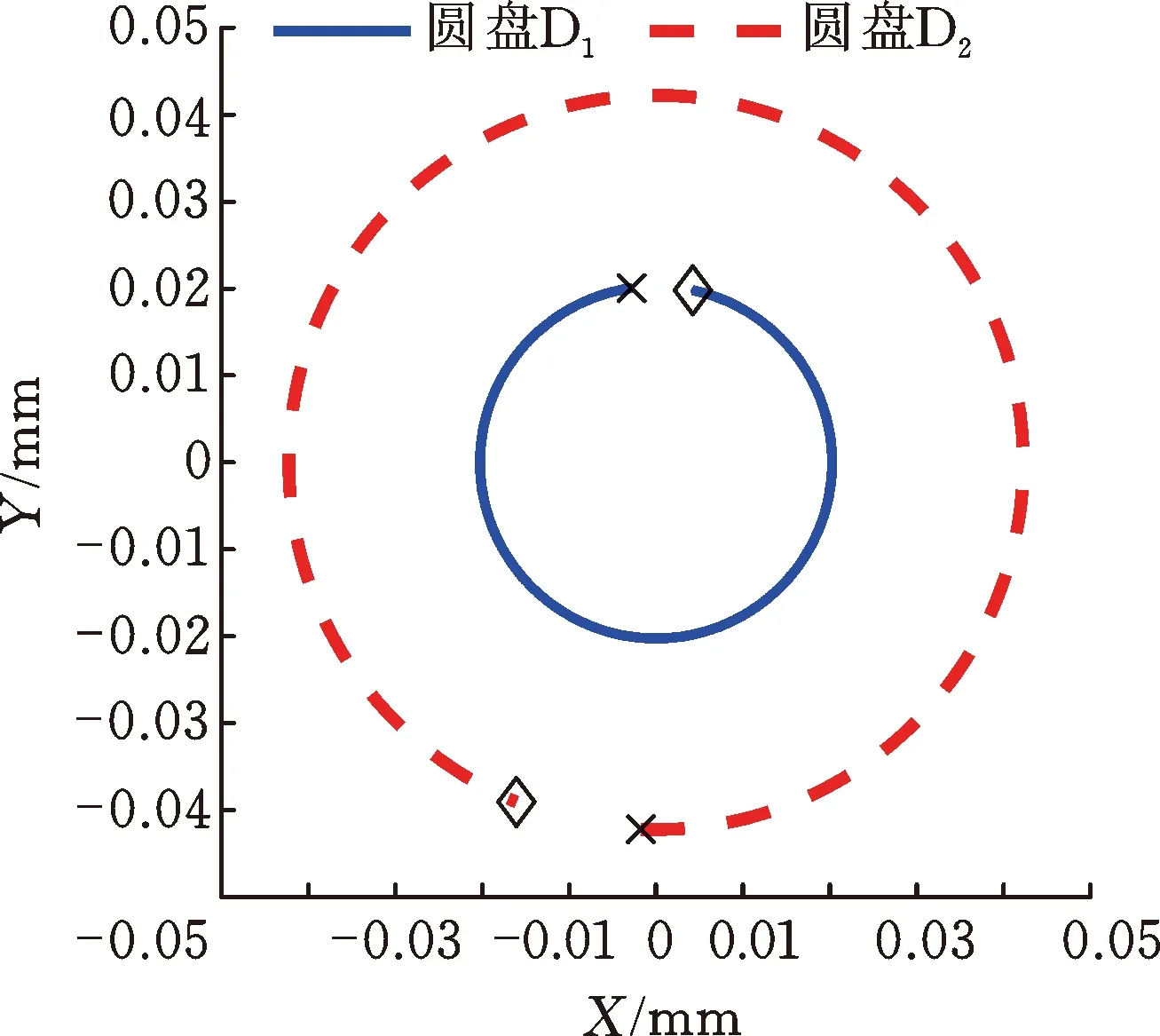
(b) 二階正進(jìn)動固有頻率

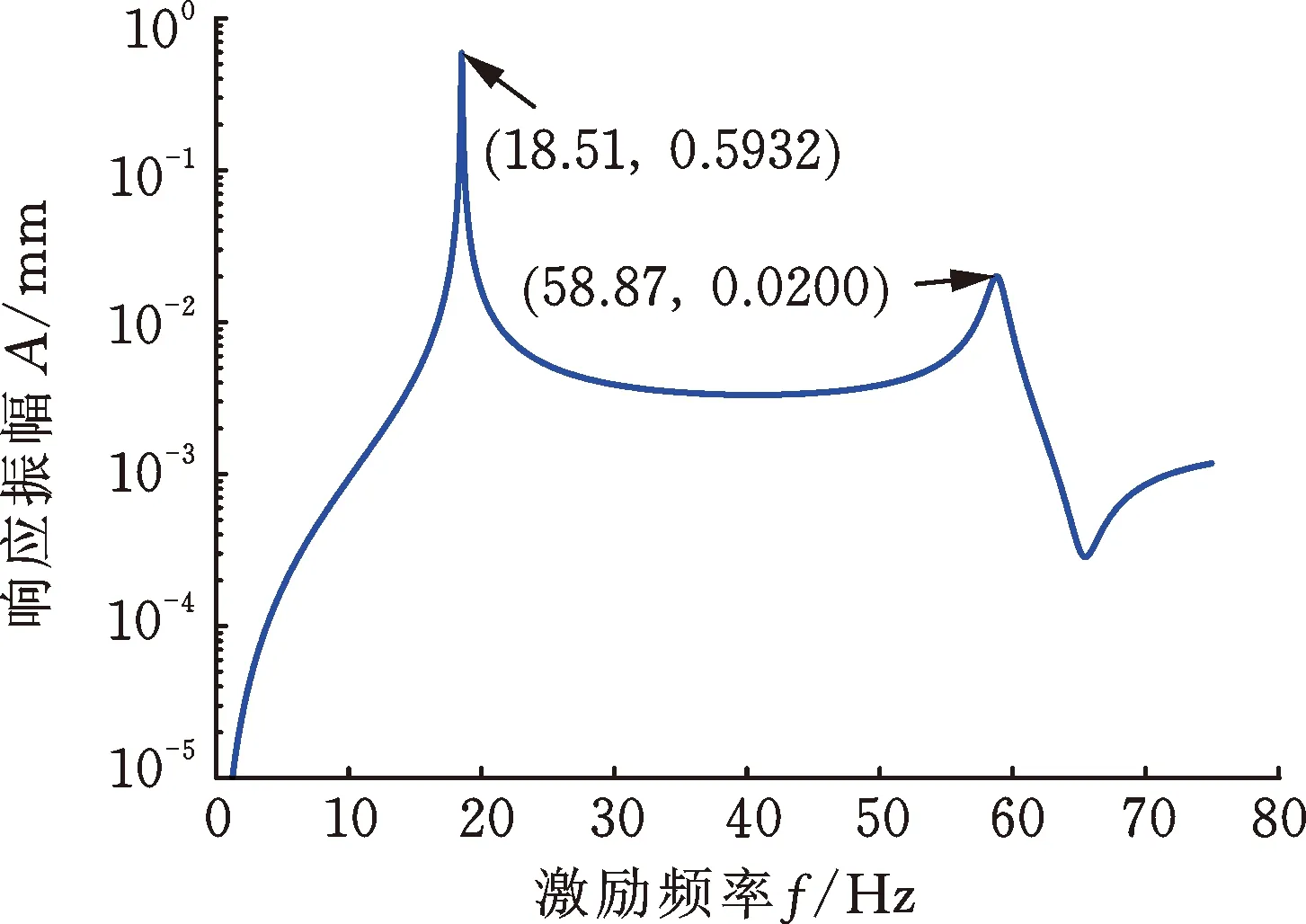
(a) 圓盤D1的響應(yīng)振幅

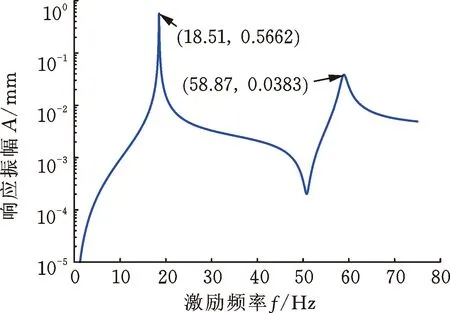
(b) 圓盤D2的響應(yīng)振幅圖7 反向旋轉(zhuǎn)掃頻激勵力下圓盤的響應(yīng)Fig.7 Disk response under counter-rotating exciting forces

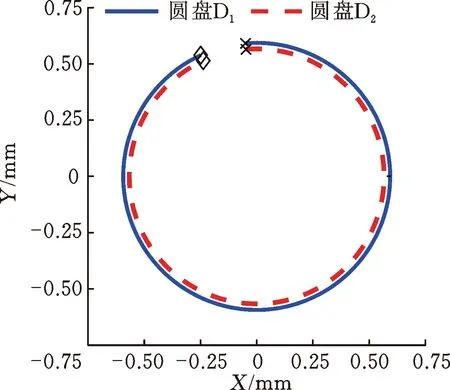
(a) 一階反進(jìn)動固有頻率

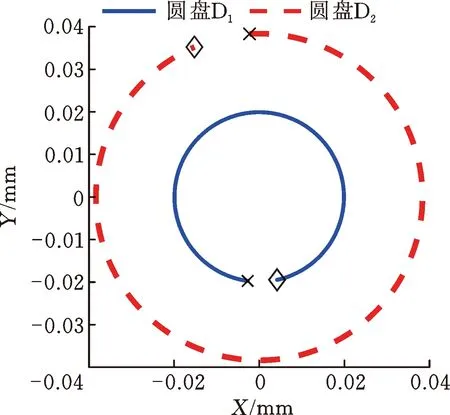
(b) 二階反進(jìn)動固有頻率

3.3 單向簡諧掃頻激勵下轉(zhuǎn)子系統(tǒng)動力學(xué)響應(yīng)

當(dāng)轉(zhuǎn)子轉(zhuǎn)速為3000 r/min時，通過磁軸承在轉(zhuǎn)子跨中位置處的X方向施加簡諧激勵力QX=(cosωt,0,0,0)T，兩個圓盤的響應(yīng)幅值如圖9所示。此時，響應(yīng)峰值對應(yīng)的頻率等于轉(zhuǎn)速為3000 r/min轉(zhuǎn)子系統(tǒng)的反進(jìn)動/正進(jìn)動固有頻率，轉(zhuǎn)子系統(tǒng)的反進(jìn)動/正進(jìn)動模態(tài)均被激發(fā)，原因如下：由歐拉公式可知cosωt=0.5(ejωt+e-jωt)，因此作用在轉(zhuǎn)子系統(tǒng)上的單向簡諧激勵力可以等效為同向旋轉(zhuǎn)激勵力QX1=0.5(cosωt,sinωt,0,0)T和反向旋轉(zhuǎn)激勵力QX2=0.5(cos(-ωt),sin(-ωt),0,0)T之和，二者分別激發(fā)了轉(zhuǎn)子系統(tǒng)的正進(jìn)動/反進(jìn)動模態(tài);當(dāng)對轉(zhuǎn)子系統(tǒng)分別施加激勵力QX1和QX2時，計(jì)算所得的響應(yīng)之和與圖9相同，從而驗(yàn)證了上述分析的準(zhǔn)確性。

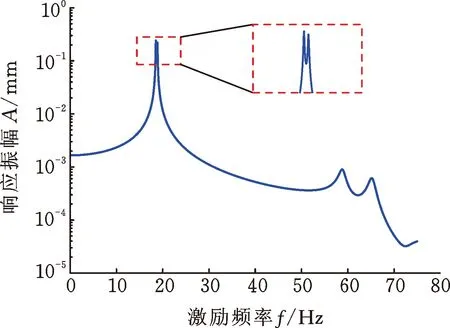
(a) 圓盤D1的響應(yīng)振幅

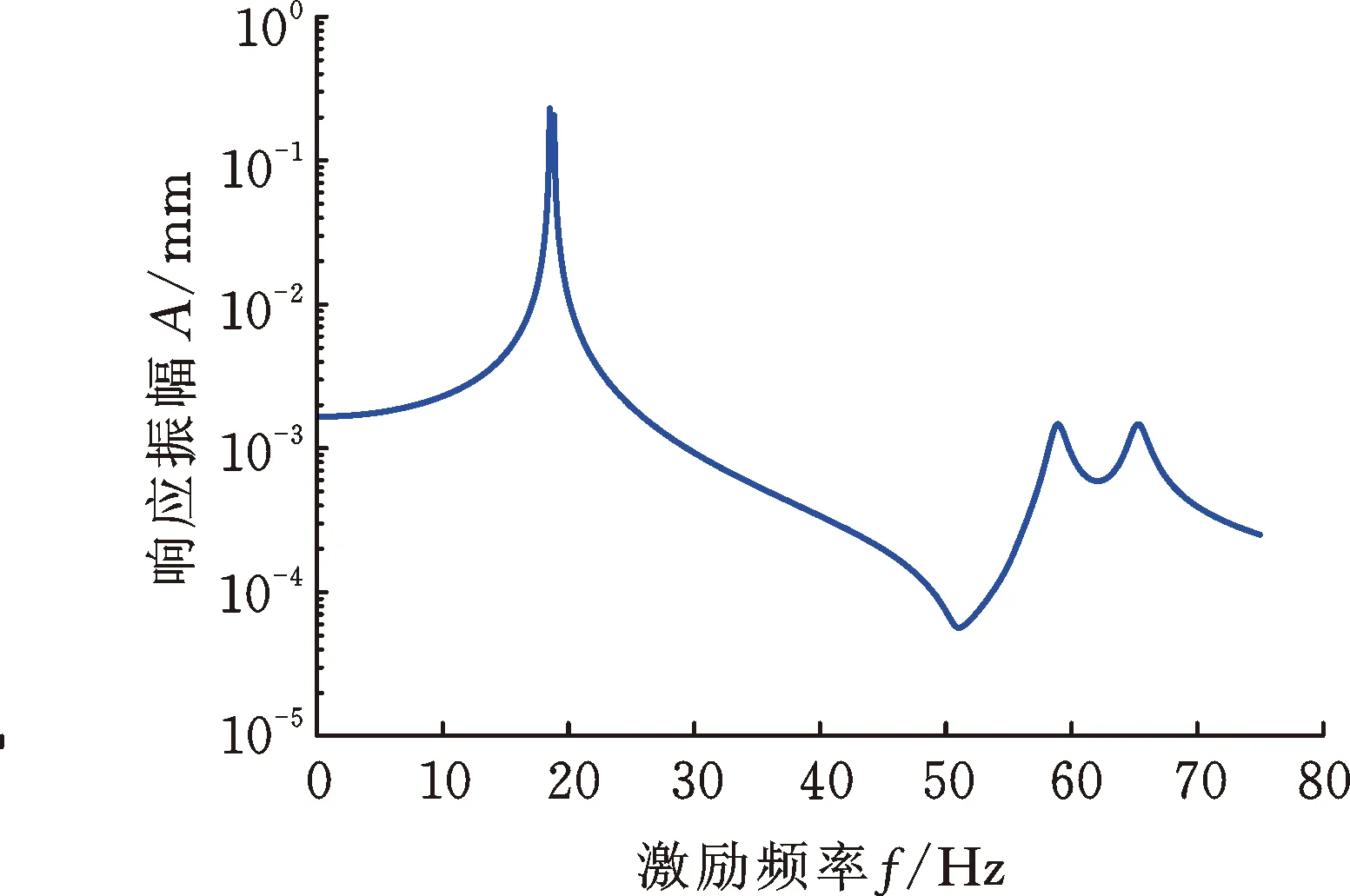
(b) 圓盤D2的響應(yīng)振幅圖9 單向簡諧掃頻激勵下圓盤的響應(yīng)Fig.9 Disk response under unidirectional harmonicsweep excitation

圖10顯示了響應(yīng)峰值處圓盤的進(jìn)動狀態(tài)，可以看出，由于陀螺力矩的耦合作用，故X方向的激勵使Y方向出現(xiàn)了響應(yīng)幅值。由于兩個方向的響應(yīng)幅值存在差異，因此轉(zhuǎn)子系統(tǒng)的進(jìn)動軌跡為橢圓形。

在不同的轉(zhuǎn)速下，通過磁軸承在轉(zhuǎn)子跨中位置施加簡諧激勵力QX=(cosωt，0，0，0)T，轉(zhuǎn)子系統(tǒng)的瀑布圖見圖11。由上述分析可知，此時轉(zhuǎn)子系統(tǒng)的反進(jìn)動/正進(jìn)動模態(tài)均被激發(fā)，由于一階反進(jìn)動/正進(jìn)動固有頻率在低轉(zhuǎn)速時較為接近，因此在瀑布圖中的一階反進(jìn)動/正進(jìn)動固有頻率處未出現(xiàn)明顯的雙共振峰。由于陀螺力矩使二階反進(jìn)動/正進(jìn)動固有頻率的差值隨著轉(zhuǎn)速的增大而逐漸增大，所以從瀑布圖中可以看出二階反進(jìn)動/正進(jìn)動固有頻率線隨著轉(zhuǎn)速的增大逐漸分離，且在較大轉(zhuǎn)速時的二階反進(jìn)動/正進(jìn)動固有頻率處均出現(xiàn)明顯的共振峰。本節(jié)得到的轉(zhuǎn)子系統(tǒng)在單向簡諧掃頻激勵下的進(jìn)動狀態(tài)與文獻(xiàn)[5-6]中的實(shí)驗(yàn)結(jié)果相同，從而驗(yàn)證了本文磁軸承激勵下轉(zhuǎn)子系統(tǒng)動力學(xué)建模的準(zhǔn)確性。

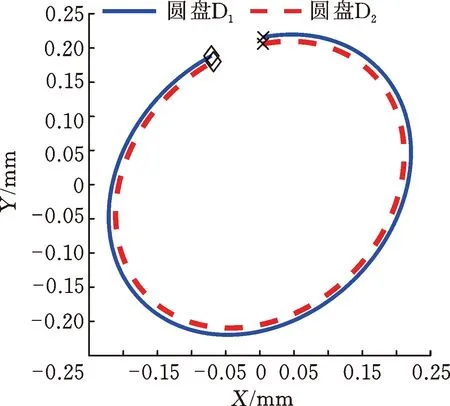
(a) 一階反進(jìn)動固有頻率

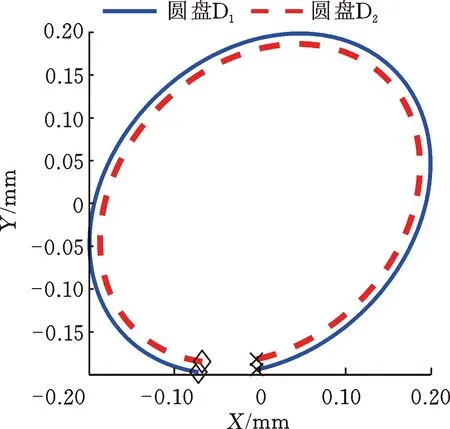
(b) 一階正進(jìn)動固有頻率

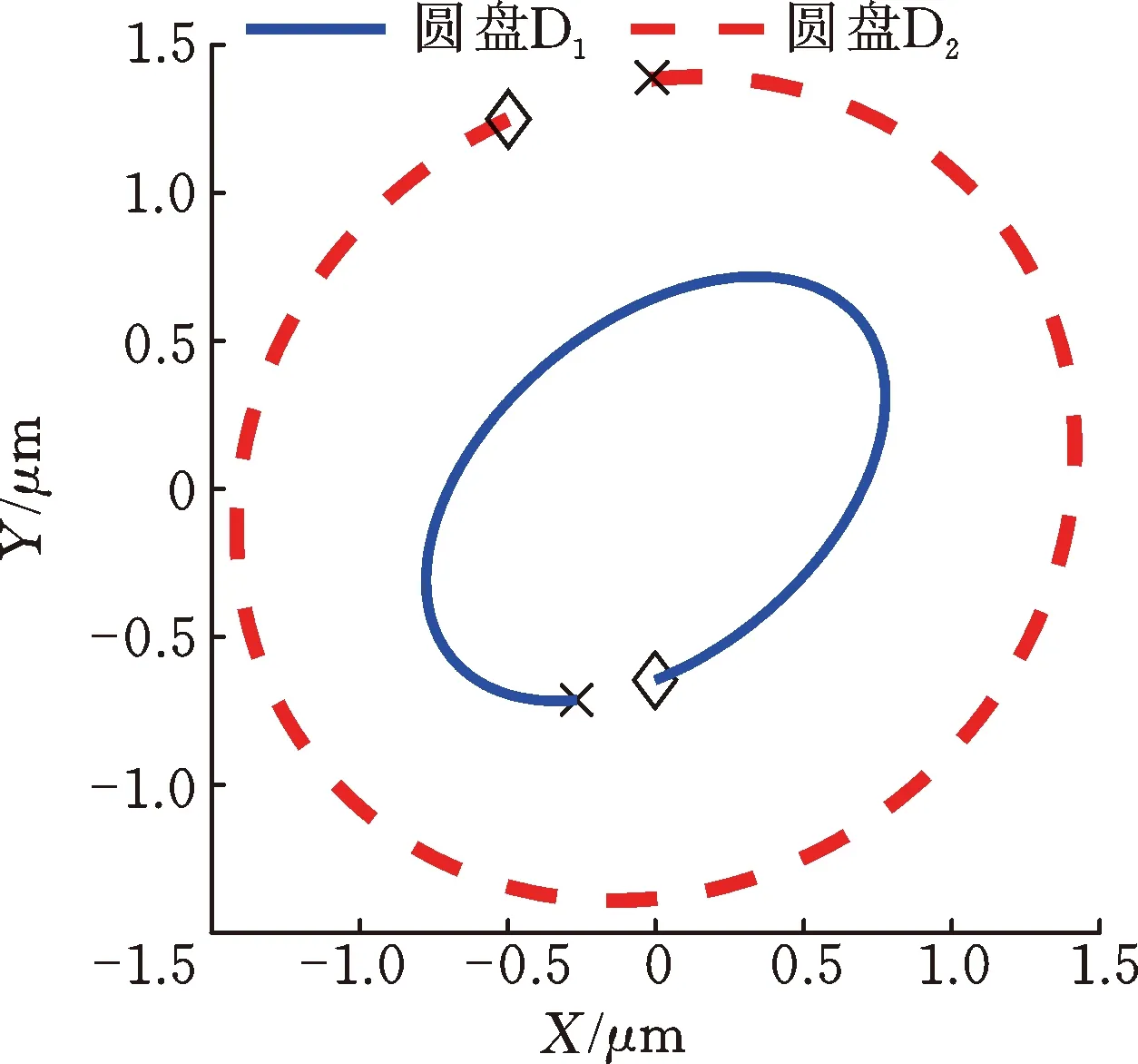
(c) 二階反進(jìn)動固有頻率

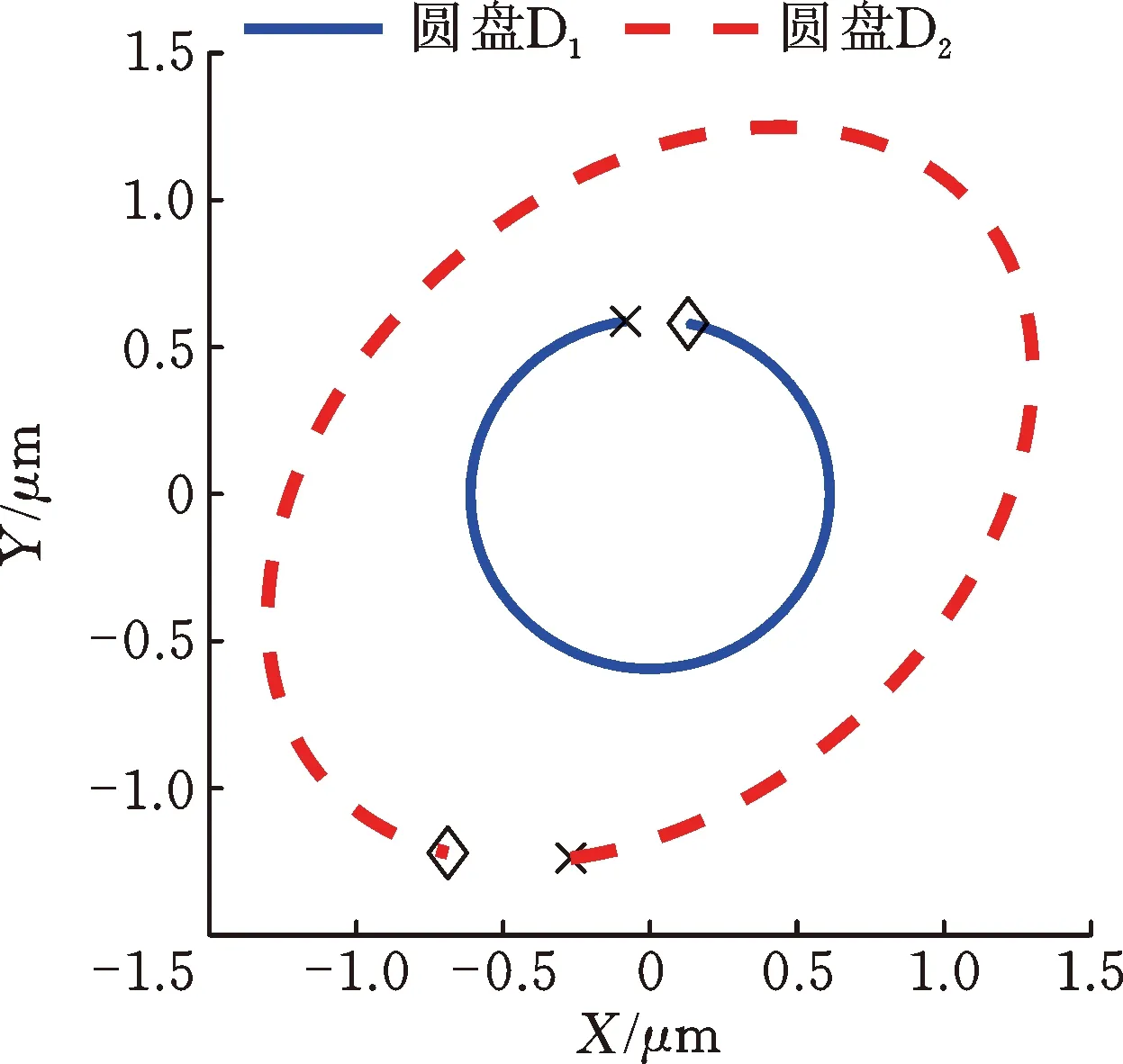
(d) 二階正進(jìn)動固有頻率

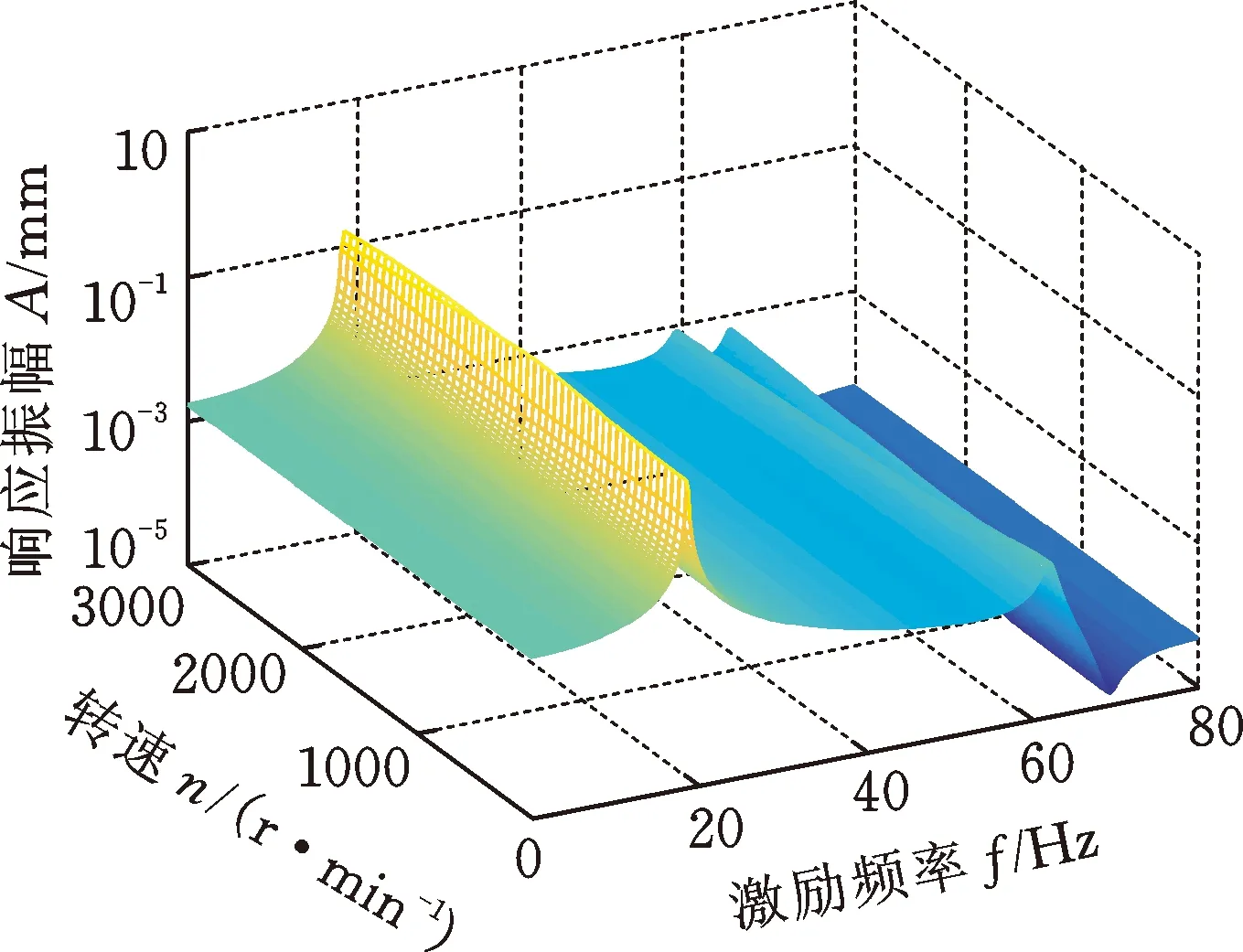
(a) 圓盤D1

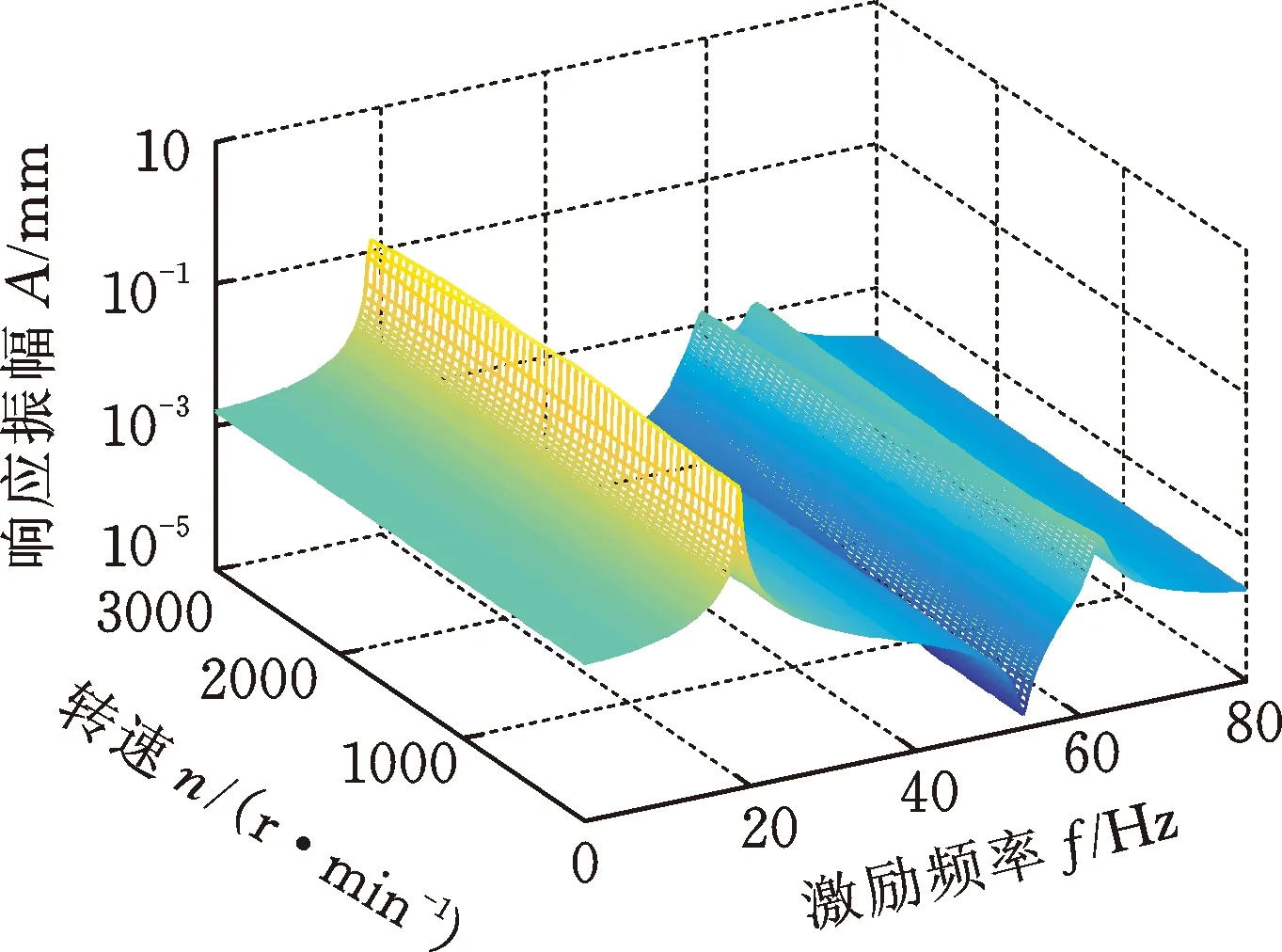
(b) 圓盤D2圖11 轉(zhuǎn)子系統(tǒng)的瀑布圖Fig.11 Waterfall plot of the rotor system

3.4 雙向簡諧掃頻激勵下轉(zhuǎn)子系統(tǒng)動力學(xué)響應(yīng)

當(dāng)轉(zhuǎn)子轉(zhuǎn)速為3000 r/min，通過磁軸承在轉(zhuǎn)子跨中位置的X和Y方向分別施加簡諧激勵力QX=cosωt和QY=cos(ωt+α)，在不同相位值α下，兩個圓盤的進(jìn)動狀態(tài)如表1所示。從表中可以看出此時轉(zhuǎn)子系統(tǒng)的進(jìn)動狀態(tài)取決于兩個方向上激勵力的相位差。當(dāng)相位差為π/2或3π/2時，轉(zhuǎn)子系統(tǒng)的反進(jìn)動或正進(jìn)動模態(tài)被激發(fā)，轉(zhuǎn)子系統(tǒng)以圓軌跡進(jìn)動；而相位差為其他值時，轉(zhuǎn)子系統(tǒng)的反進(jìn)動/正進(jìn)動模態(tài)均被激發(fā)，轉(zhuǎn)子系統(tǒng)以橢圓軌跡進(jìn)動。由此可知，在使用磁軸承對轉(zhuǎn)子系統(tǒng)做雙向簡諧掃頻激勵時，兩個方向上激勵力相位差的選取是至關(guān)重要的。

表1 激勵力相位差對轉(zhuǎn)子系統(tǒng)進(jìn)動狀態(tài)的影響Tab.1 Effect of the phase difference of the excitation force on the whirl state of the rotor system

4 結(jié)論

(1)同向旋轉(zhuǎn)的掃頻激勵力激發(fā)了轉(zhuǎn)子系統(tǒng)的正進(jìn)動模態(tài)，而反向旋轉(zhuǎn)的掃頻激勵力激發(fā)了轉(zhuǎn)子系統(tǒng)的反進(jìn)動模態(tài)，兩種情況下轉(zhuǎn)子系統(tǒng)均以圓軌跡進(jìn)動。

(2)單向簡諧激勵力可以分解為同向旋轉(zhuǎn)激勵力和反向旋轉(zhuǎn)激勵力之和，因此在單向簡諧掃頻激勵力作用下，轉(zhuǎn)子系統(tǒng)的反進(jìn)動/正進(jìn)動模態(tài)均被激發(fā)，轉(zhuǎn)子系統(tǒng)以橢圓軌跡進(jìn)動。

(3)在雙向簡諧掃頻激勵力作用下，轉(zhuǎn)子系統(tǒng)的進(jìn)動方向和進(jìn)動軌跡取決于兩個激勵力的相位差。