一種頻偏條件下新的Chirp-BOK分數域解調方法
寧曉燕, 聶毅帆, 孫志國, 王秋瀅
(信息與通信工程學院 哈爾濱工程大學,黑龍江 哈爾濱 150001)
擴頻通信是一種發射信號占用帶寬遠遠大于發送信息所需帶寬最大值的傳輸方式,由于其具有抗干擾能力強、隱蔽性好、易于實現碼分多址等諸多優點被廣泛應用于定位、通信、測距等領域。線性調頻信號擴頻(chirp spread spectrum, CSS)作為多種擴頻技術的一種,在一定的符號間隔內,Chirp信號頻率掃過一定的范圍,因此占用的頻帶寬度比信息帶寬大得多,實現了對信息的頻譜擴展,因此可將其視為一種擴頻信號[1]。
Tsai等[2]在匹配濾波相干解調基礎上進一步分析了在Rayleigh和Rician衰落信道下采用Chirp信號抗多徑干擾的優勢。基于Chirp信號的多用戶通信、混合擴頻通信等的提出,進一步提升通信系統容量和性能[3-5]。基于Chirp信號的Rake接收的提出,進一步提升系統的抗多徑性能[6]。近年來,多種技術與擴頻通信技術相結合也逐漸成為研究熱點。分數域傅里葉變換(fractional Fourier transform, FrFT)作為傅里葉變換的推廣,其以Chirp信號為基函數,因此Chirp信號在適當的分數域出現聚斂現象[7-8]。在文獻[9-10]中,利用了Chirp信號分數域特性進行參數估計;在文獻[11]中提出將Chirp信號用作OFDM系統的同步信號;在文獻[12]中提出了一種基于FrFT的Chirp信號擴頻調制算法,以二進制數字調制解調為例,探討了基于分數域傅里葉變換的Chirp非相干解調的相關理論問題。通過與匹配濾波解調法的比較可知,FrFT非相干解調的優勢是不受到相位誤差的影響[11],且在對抗多普勒頻移和碼同步誤差的影響時與時域相干解調是相同的[12];分數域非相干解調的性能劣勢是沒有利用到相位信息導致的。
為了保留FrFT非相干解調對抗相位偏差的優勢,并且提升對抗多普勒頻移和碼同步誤差的能力,本文在FrFT非相干解調的基礎上進行了改進,提出了峰值搜索-FrFT非相干解調,與傳統方法進行了對比分析,證明了該方法在頻偏條件下具有更好的誤碼率性能。
1 Chirp-BOK調制解調
1.1 Chirp-BOK調制方案
基于二進制正交鍵控(binary orthogonal keying,BOK),提出了Chirp-BOK調制方式。它利用了Chirp信號的掃頻特性,對Chirp信號的正、反調頻率進行信息攜帶處理,達到信號調制解調的目的,這種方式具有結構簡單、低復雜度、低功耗等特點,是Chirp信號的常用調制方式[13-14]。設k為正整數,本文使用調頻率為k的升頻信號(Up-Chirp)表示“1”,使用調頻率為-k的降頻信號(Down-Chirp)表示“0”。Chirp信號表達式為:
(1)
Chirp-BOK調制框圖如圖1所示。
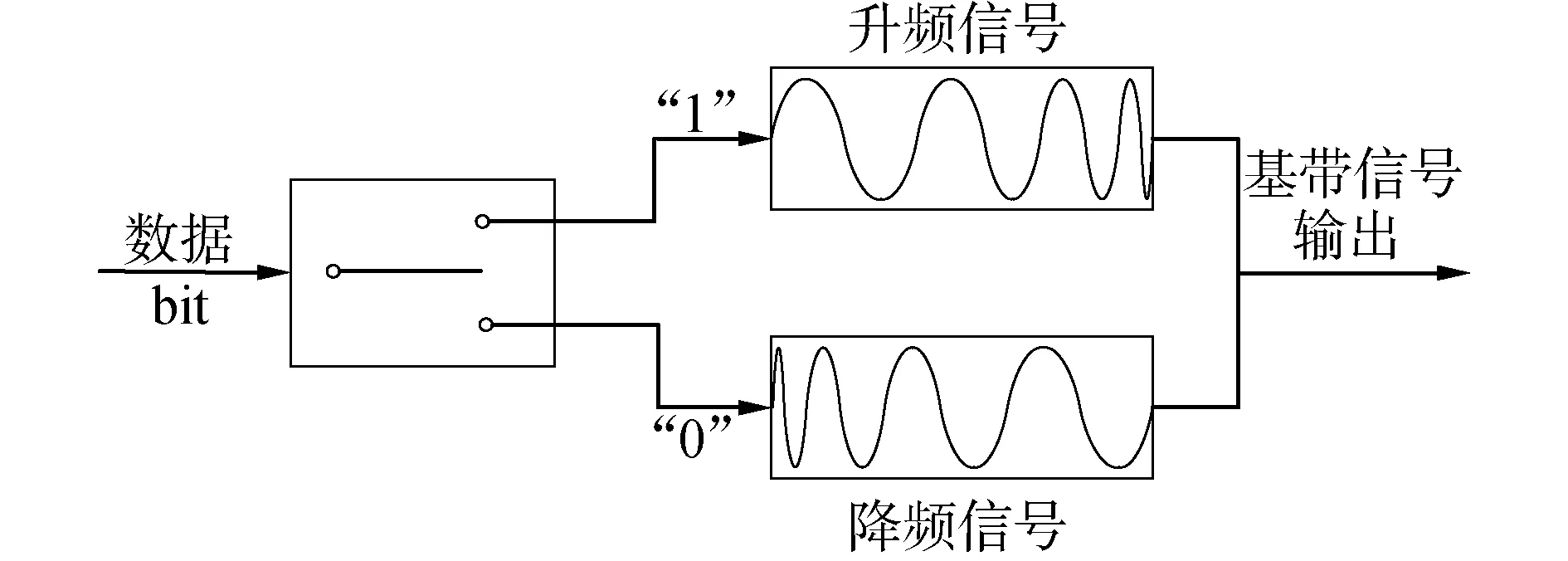
圖1 Chirp-BOK調制Fig.1 The bock diagram of Chirp-BOK modulation
1.2 解調方案
1.2.1 匹配濾波相干解調
Up-Chirp與調頻率相反的Down-Chirp信號互為匹配濾波函數[11],因此接收端解調框圖如圖2所示。

圖2 匹配濾波解調Fig.2 The bock diagram of MF demodulation
以升頻信號為例,匹配濾波輸出如圖3(a)所示,非匹配濾波輸出如圖3(b)所示。
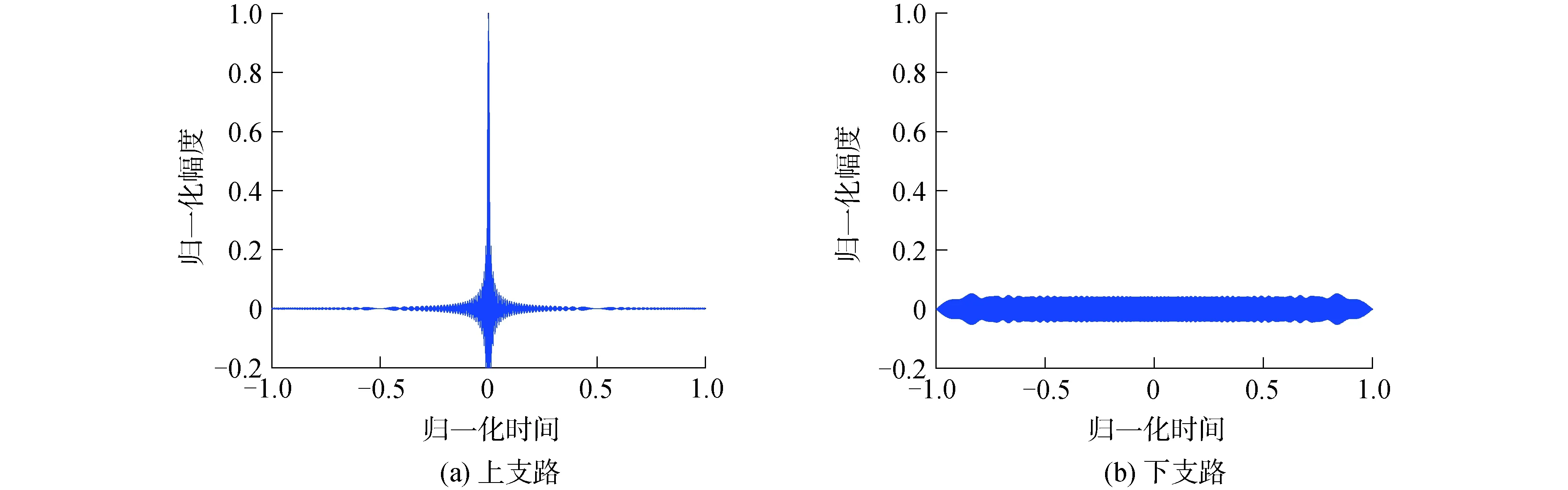
圖3 濾波器輸出波形Fig.3 Output waveform of filter
1.2.2 分數域非相干解調
分數域傅里葉變換可以看作是傳統傅里葉變換的一種推廣。正余弦函數是傅里葉變換的基函數,而Chirp函數正是其調頻率對應階次的分數域傅里葉變換的基函數[15]。分數域傅里葉變換是公認的適合處理Chirp信號的工具,分數域傅里葉變換的定義式[16]為:

(2)
式中:下標p為分數域傅里葉變換的階次;α=pπ/2;u為分數域坐標;t為時域坐標;算子核K(α;u,t)定義為:
2utcscα+t2cotα)]
(3)

調頻率為k的Chirp信號經過p=-2arccot(k/π)階FrFT后出現聚斂峰值,該階次p被稱為Chirp信號的最優階次[7];由高斯分布線性變換不變性,高斯白噪聲經過p階分數域傅里葉變換后仍然是高斯白噪聲。
根據歐拉公式可以將調頻率為k的實Chirp信號拆分為2個調頻互為相反數的復Chirp信號:
(4)
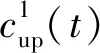
同理,調頻率為-k的實Chirp信號拆分為2個調頻互為相反數的復Chirp信號:
(5)
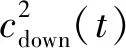
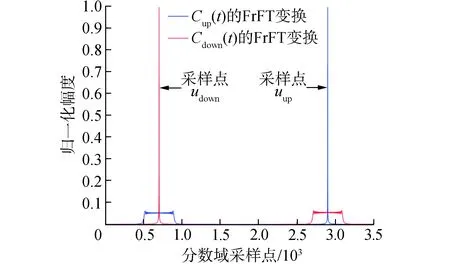
圖4 p階分數域譜Fig.4 Impact of p order fractional domains
1) 定點采樣解調。
根據Chirp信號的分數域性質,對接收到的Chirp信號進行分數域傅里葉變換,然后采樣判決[17-18]。FrFT非相干解調框圖如圖5所示。因為該方法是在固定頻點進行采樣,為了與本文提出的方法進行區分,稱之為定點采樣-FrFT非相干解調。
2) 峰值搜索解調。
針對存在多普勒頻移和碼同步誤差時定點采樣法性能下降嚴重的問題,本文提出了峰值搜索-FrFT非相干解調。峰值搜索示意圖如圖6所示,圖中N為奇數。當分數域峰值位置存在偏移,如果還在原來的位置進行采樣判決,系統的性能將嚴重下降,甚至無法解調。但是峰值位置的大致區域是可以確定的,如果將定點采樣擴展為區域峰值采樣,只要該區域的范圍超過最大偏移的范圍,即可以保證峰值一定能落在該區域內。然后在采樣得到的2N個值中搜索峰值,由峰值所在區域得到判決結果。
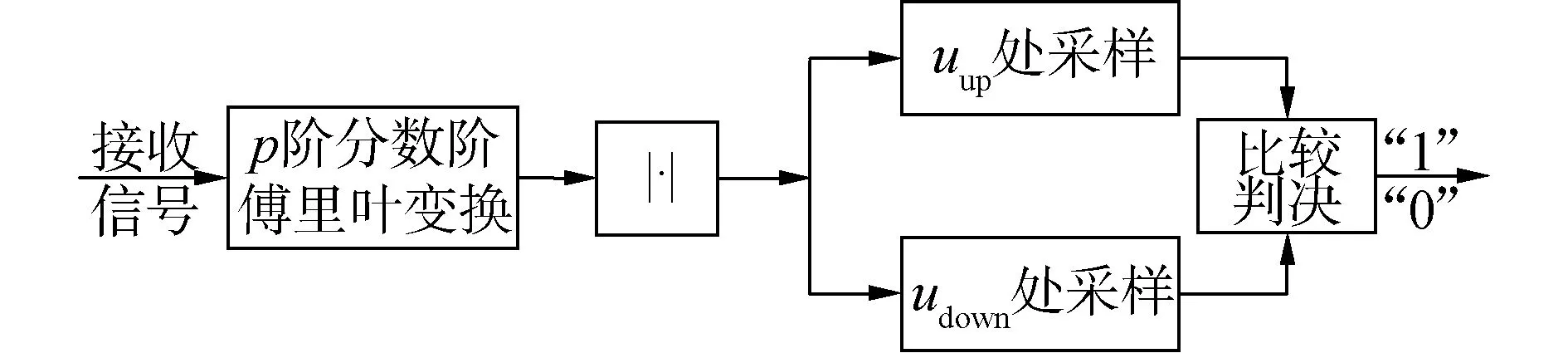
圖5 定點采樣-FrFT非相干解調框圖Fig.5 The bock diagram of Fixed point sampling-FrFT non-coherent demodulation
峰值搜索法的解調框圖如圖7所示。基帶信號先經過p階FrFT,取模值后得到Chirp信號的分數域譜,以cup(t)和cdown(t)對應位置uup和udown為參考點將定點采樣擴展為區域峰值搜索。
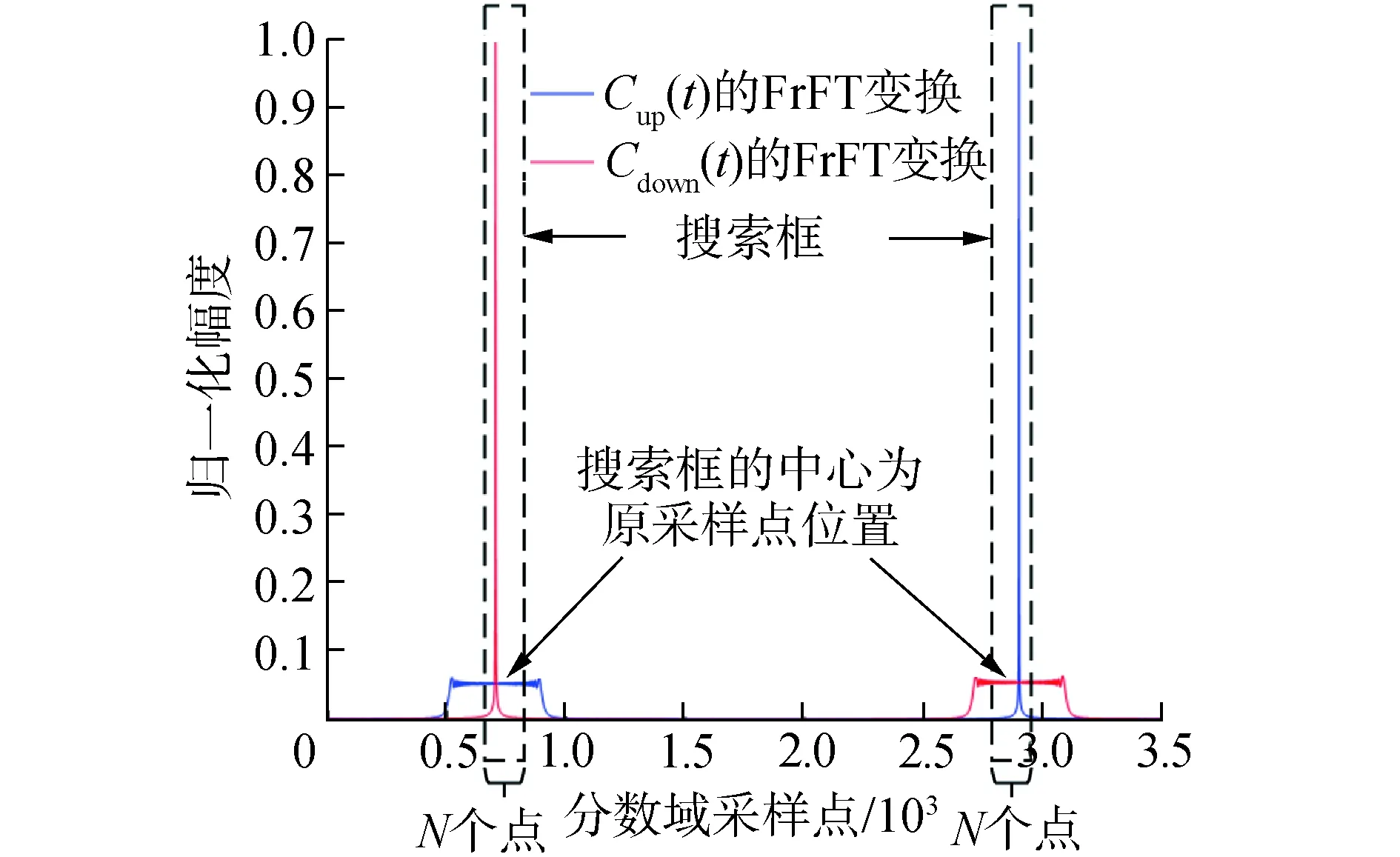
圖6 分數域峰值搜索示意Fig.6 Impact of peak search
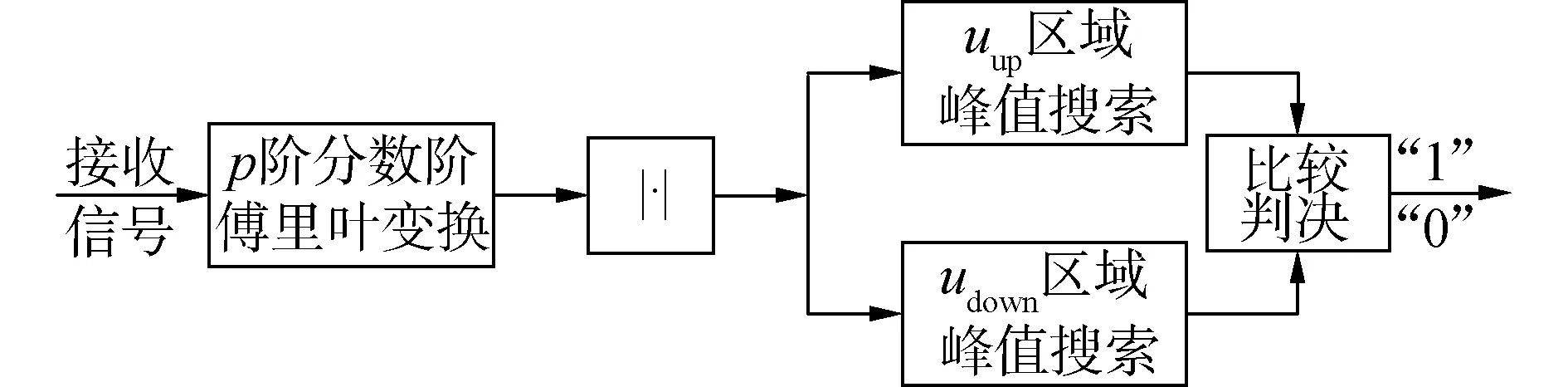
圖7 峰值搜索-FrFT非相干解調框圖Fig.7 The bock diagram of peak search-FrFT non-coherent demodulation
2 性能分析
2.1 AWGN信道下性能分析
2.1.1 匹配濾波法的性能分析
對于匹配濾波相干解調,根據二進制最佳接收公式可以得出其誤碼率公式:
(6)
式中:ρ為升頻信號和降頻信號的相關系數;Eb為碼元能量;n0為帶限高斯白噪聲的單邊功率譜密度。
2.1.2 定點采樣法的性能分析
以調頻率為k的Chirp信號為例,經過AWGN信道后接收到的信號為:
r(t)=Ae2πf0t+πkt2+n(t)ejθ
(7)
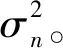
接收信號r(t)經過p階FrFT后,在u1處采樣可以得到:
Rp(uup)=Aejθ0+n(uup)ejθ1
(8)
而在u2處采樣可以得到:
Rp(udown)=ξAejθ0+n(udown)ejθ2
(9)
式中:A為經過最優階次變換的分數域采樣值;ξA是經過非最優階次變換的分數域采樣值,ξ和θ0是與Chirp信號具體參數有關的值;θ1和θ2是由噪聲引入的隨機相位。
調整相位可以得到:
(10)
兩路信號取模值可以得到:
(11)
式中abs(·)表示取模值。
由隨機信號分析可知,abs(Rp(uup))的抽樣值Rup和abs(Rp(udown))的抽樣值Rdown服從萊斯分布。它們的概率密度分布分別為:
(12)
式中I0(·)為第1類零階修正貝塞爾函數。
以升頻信號為例,定點采樣法判決正確的概率為:
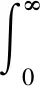
(13)
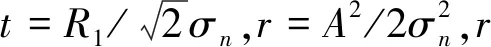
當發送信號為降頻信號時,判決正確的概率Pdown=Pup。
當發送升頻信號和降頻信號的概率相等時,定點采樣-FrFT非相干解調的誤碼率為:
(14)
2.1.3 峰值搜索法的性能分析
對于峰值搜索法,由2點比較判決擴展為2N個點互相比較判決。首先對存在峰值區域的N個點進行搜索,尋找最大值。在AWGN信道且同步準確的情況下,第(N+1)/2個點即峰值所在位置。然后對不存在峰值區域的N個點進行搜索,尋找最大值。將這2N個點記為x1,x2,…,xi,…,x2N,xi的采樣值為:
xi=ξiA+niejθi
(15)
式中:ξiA為每個采樣點的幅值,ξi和θi是與Chirp信號具體參數有關的值,0<ξi≤1。abs(xi)服從萊斯分布,它們的概率密度函數為:
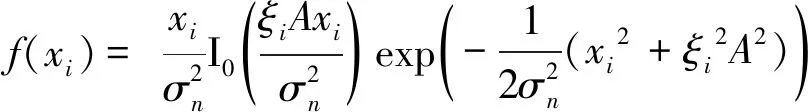
(16)
當xi,i=1,2,…,N為最大值時可以正確解調,則峰值搜索法判決正確的概率為:
xi>x2N|xi)f(xi)d(xi)
(17)
式中2N個采樣點之間相互獨立,互不影響,式(17)可以化簡為:
(18)
式中:
(19)
經過化簡,可得峰值搜索法誤碼率為:
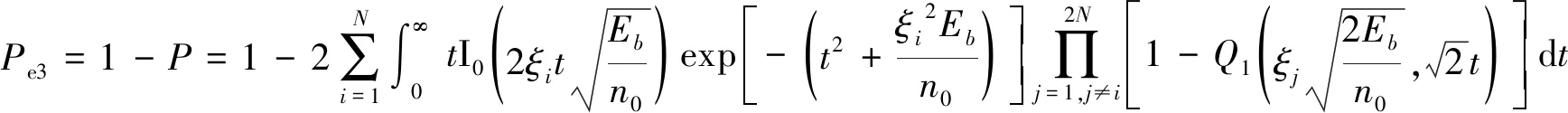
(20)
2.2 頻偏對分數域解調法的影響
以調頻率為k的Chirp信號為例,分析頻率偏移對Chirp信號FrFT非相干解調的影響,以證明將定點采樣改進為區域峰值搜索的必要性和優越性。
首先,頻偏主要來源于位同步誤差、多普勒頻移和收發端接收機參數差異。當存在同步誤差時,本地同步時間與信號實際到達時間存在時刻τ的延時或超前,信號表達式為:
c(t)=cos(2πf0(t+τ)+πk(t+τ)2)
(21)
把τ看做定值,則上式可以化簡為:
c(t)=cos(πfmt+πkt2+Δ)
(22)
式中:fm=f0+kτ/2,Δθ=2πf0τ+πkτ2。可以看到,Chirp信號的時間τ的同步誤差可以轉化為頻率的頻移kτ/2和相位的偏移Δθ;同時,由于存在時間偏差,因此只有部分信號被利用到,造成了能量的損失。
當存在多普頻移時, Chirp信號中心頻率發生偏移,因為入射角的不同多普勒頻移的值將會出現變化,取最大值時Chirp信號表達式為:
c(t)=cos(2π(f0+fd)t+πkt2+φ)
(23)
可以看到,多普勒頻移造成的影響首先是中心頻率偏移fd,與同步誤差造成的影響是類似的。
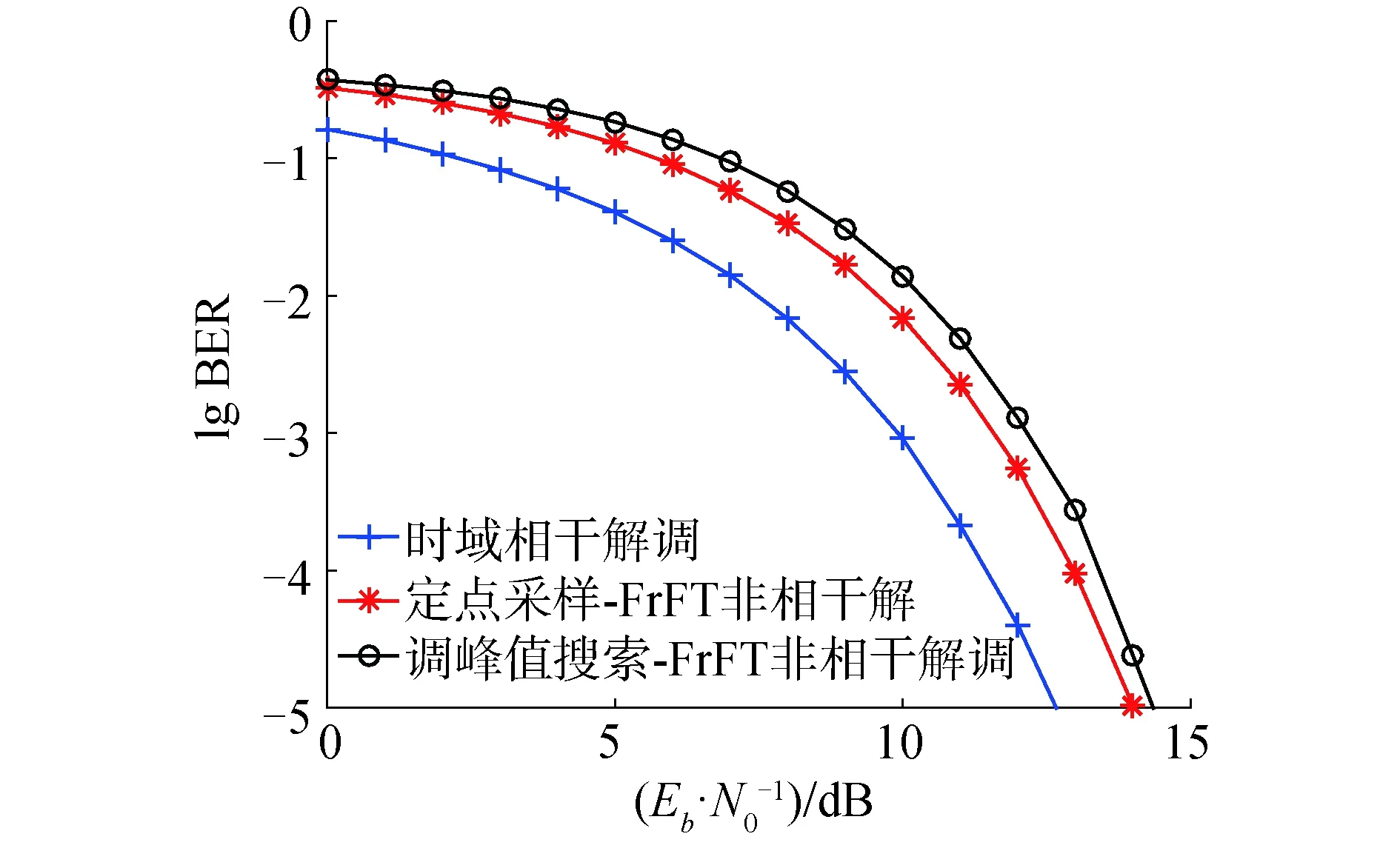
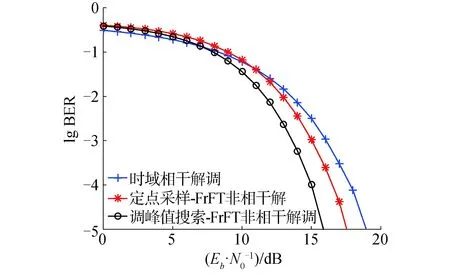
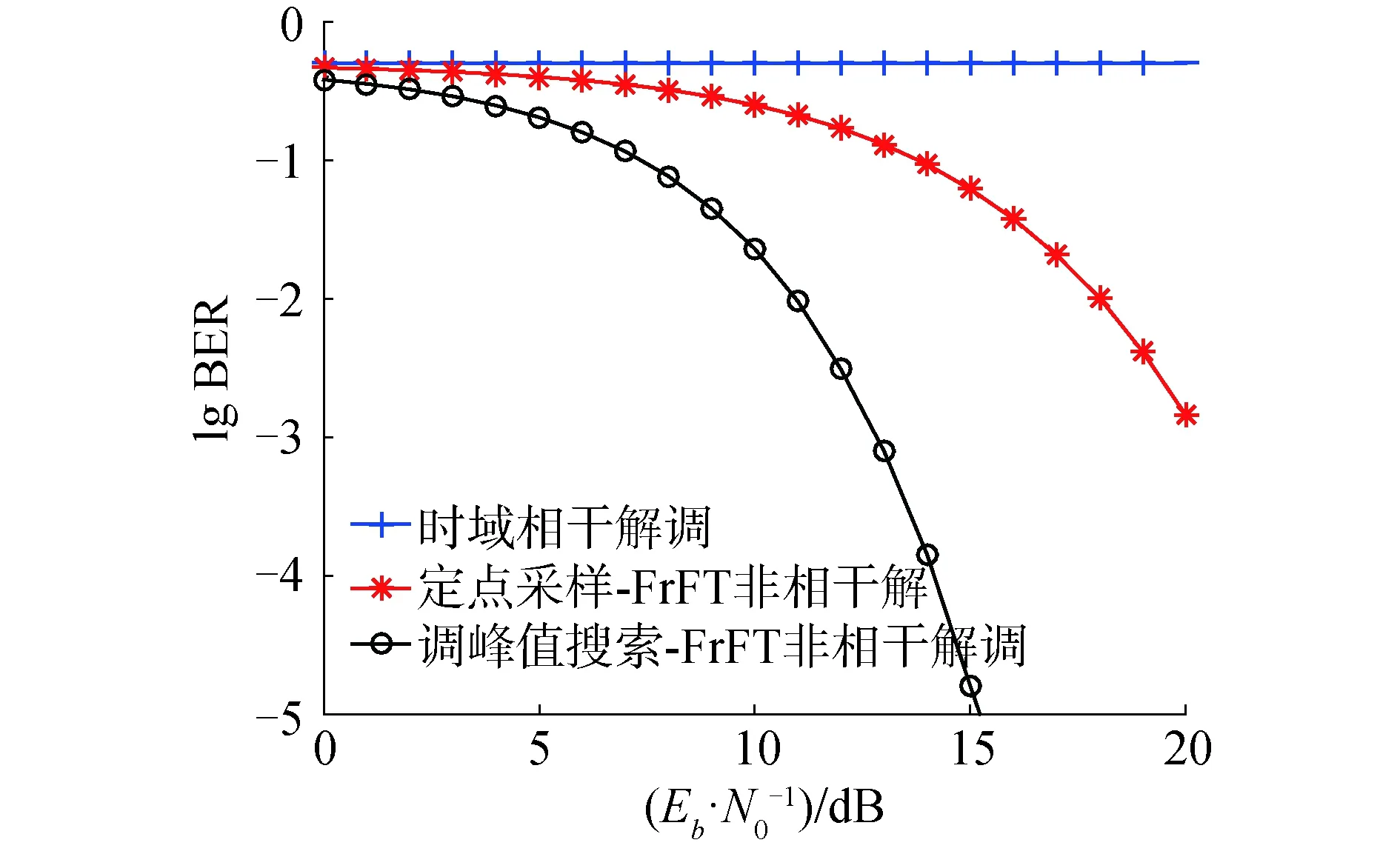
下面分析頻偏對采樣點的具體影響。首先將同步誤差和多普勒頻移造成的頻偏統一記為fd。根據1.2.2節中的分析,以升頻信號為例,在p階分數域的峰值聚斂位置為uup=f0sinα,能量集中在|u-uup| c(t)=cos(2πfmt+πkt2) (24) 新的峰值聚斂位置為um=(f0+fd)sinα,偏移距離fdsinα。當頻偏較大時,能量聚斂位置甚至會完全偏離該區域,如果仍以uup為采樣點,則無法正確解調出信息。 當采樣點移動的區域仍在|u-uup| c(t)=exp(j2πfmt+jπkt2) (25) 將c(t)代入分數域變換公式得: (26) 當k=-cotα,u=f0sinα時,可得: (27) 化簡得: (28) 取包絡得: (29) 可以看出abs(Cp(u))的值與T和fd有關,當T固定時,fd越大,采樣值越小。 綜上,同步誤差、多普勒頻移和接收機收發3端參數差異可以統一轉換為中心頻率的偏移和能量的損失。映射到分數域,對應著峰值位置的偏移和采樣值的降低,嚴重影響了定點采樣-FrFT非相干解調的性能。因此本文提出了峰值搜索-FrFT非相干解調來改善頻偏下的性能。 引入頻率偏移后,峰值搜索-FrFT非相干解調仍然為2N個點互相比較判決,只是峰值所在位置可能不再是第(N+1)/2個點。推導過程與AWGN信道下相同,故誤碼公式也與式(20)相同。系數ξi與引入頻偏的Chirp信號分數域采樣值有關。 圖8對比了Chirp-BOK調制的3種解調方式在AWGN信道下的誤碼率曲線。仿真參數:帶寬20 MHz、碼長10 μs、搜索點數為3個采樣點。從圖8中可以看出相干解調的性能最好;而峰值搜索-FrFT方法的性能相比于定點采樣-FrFT性能下降不超過0.5 dB。 圖8 AWGN信道下3種解調方式性能對比Fig.8 Performance comparison of three demodulation methods in AWGN channel 圖9給出了AWGN信道下峰值搜索-FrFT的理論曲線和仿真曲線。搜索區域長度分別設置為3、21個采樣點。從圖9中可以看出,當搜索區域的長度越小時,本方法在AWGN信道下的性能越好。因此搜索區域范圍的設置要根據頻偏動態地調整,使得搜索范圍盡可能小。 圖9 不同長度搜索區域的誤碼率曲線Fig.9 Performance comparison of different length search ranges 圖10和圖11給出了存在頻偏時3種解調方式的性能對比。通過仿真可以看出,當歸一化頻偏比為0.001 5時,峰值搜索-FrFT的誤碼率性能優于定點采樣-FrFT與相干解調。當頻偏比增大至0.002 5時,定點采樣-FrFT與相干解調的性能迅速下降,但是峰值搜索-FrFT的性能卻幾乎不受影響。 圖10 歸一化頻偏0.001 5時3種解調方式性能對比Fig.10 Performance comparison of three demodulation methods under normalized frequency offset 0.001 5 圖11 歸一化頻偏0.002 5時3種解調方式性能對比Fig.11 Performance comparison of three demodulation methods under normalized frequency offset 0.002 5 1)該方法將傳統的定點采樣改進為采樣點周圍區域的峰值搜索,以提升對位同步誤差、多普勒頻移和收發端參數差異導致的信號頻率偏移的容忍度。 2)推導了該解調方法下AWGN信道的誤碼率公式,在AWGN信道下的性能主要受搜索長度的影響,當搜索長度越短時,性能越接近定點采樣-FrFT;當存在頻偏時,峰值搜索-FrFT可以對峰值位置進行搜索,只要滿足搜索范圍大于偏移范圍,則可以極大程度地改善誤碼率性能,而匹配濾波相干解調和定點采樣-FrFT的性能嚴重惡化。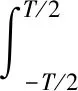
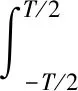
3 仿真驗證
3.1 AWGN信道下性能仿真

3.2 抗頻偏性能分析
4 結論

