一種減小中拱中垂對測深表影響的方法

周運凱，班業平，劉剛，喬利標

(上海外高橋造船有限公司，上海 200137)

船舶油量計算涉及船舶運營成本，如果油量計算出現誤差，直接影響總油價。測深表作為精確計量燃油量的工具，其精度必須得到有效的保證[1]。在船舶運營時，中拱中垂是碼頭常見的工況，因為中拱中垂而產生的測深表使用誤差很常見。因為測深表計量原理假定的是船體梁處于無形變的理論狀態，而當船舶處于中拱中垂狀態時，實際情況與理論狀態存在差異。在考慮變形，采用計算模擬船體形變后，可以減少誤差，通過這種方法，減少中拱、中垂對測深表的影響。

1 實船問題分析

通過某散貨船保單發現，在船舶卸貨前后，使用測深表計算燃油艙艙容,2種狀態下艙容相差較大，見表1、表2。

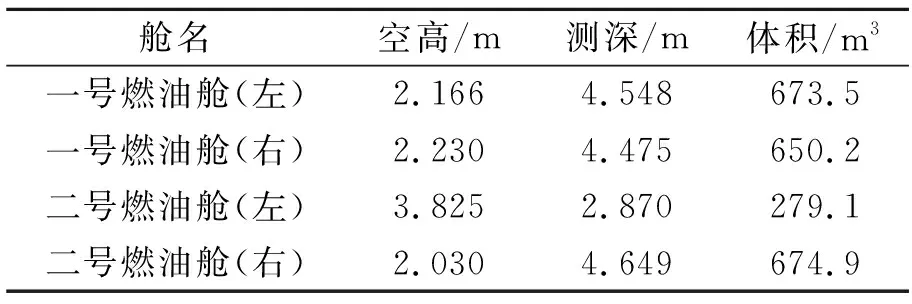
表1 卸貨前船舶狀態及燃油艙油量

表中測深指以測深管底為零點沿測深管量到液面的長度。空高指以測深管口為零點沿測深管量到液面的長度[2]。兩者之和為測深管總長。

上表為根據船舶吃水狀態，以艏艉吃水計算縱傾，結合測深值在測深表中計算的對應艙容值。由表中數據可見，在裝卸貨前后，計算出的燃油總量分別為卸貨前的2 277.7 m3，以及卸貨后的2 322.4 m3，使用測深表測算出的燃油總體積卸貨前后相差44.7 m3。

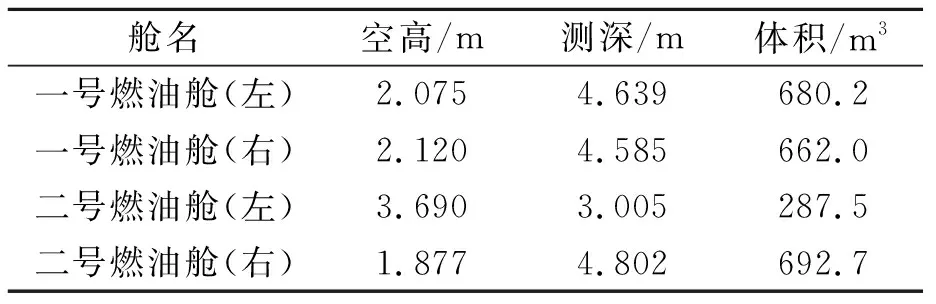
表2 卸貨后船舶狀態及燃油艙油量

由于此過程中燃油并未消耗，理論上2種狀態下計算值應該相同，在檢查模型及測深管定義無誤后，判斷誤差產生于使用測深表的計算中。

2 誤差成因及解決方案

根據SOLAS 要求，船舶縱傾定義為艏吃水值減艉吃水值[3]，常見的船舶運營使用的測深表多為使用船用軟件NAPA輸出的測深表，亦即保單中船員使用的測深表。而NAPA在輸出測深表時假定的船舶狀態為船體梁無形變的理想狀態，表中縱傾值均為艏柱吃水與艉柱吃水差符合SOLAS定義[4]，誤差源于以艏艉吃水計算縱傾時忽略了船舶實際狀態。簡單來講，當船舶存在中垂中拱時，對于處于船舶后半部的燃油艙，其真實的液面傾斜狀態更接近舯吃水與艉吃水差值，而非艏吃水與艉吃水的差值，因為使用的縱傾值與油艙實際傾斜狀態不符，導致計算存在誤差。

2.1 解決方案

精確計算艙容的核心在于需要計算出該艙室實際液面傾斜狀態下對應的假定船舶整體傾斜狀態，即所需的計算縱傾值。由于測深表中假定的船舶狀態不存在中拱中垂，要正確測算艙室容積，使用的縱傾數據必須與測深表假定的船舶狀態匹配。為此，需要模擬實際的形變狀態，由此得出艙室內液面的實際傾斜角度。考慮實際船舶運營時，船員僅能通過液位遙測裝置來獲取船舶的實際吃水狀態，液位遙測裝置僅在艏、舯、艉三處，因此實際能夠獲得的吃水數據僅3個點[5]，由于橫傾影響較小，且船舶處于穩定狀態時，形變相對簡單，使用二次曲線足以較為精確地模擬船舶實際的中拱中垂狀態。對于測深表影響主要原因在于錯誤的僅使用艏艉吃水的直線模型來計算，若將舯吃水納入考量，將模型變為曲線模型，就能夠大大減小誤差。

2.2 計算過程

將船體梁變形簡化為二次曲線，通過定義不同點的坐標位置來定位曲線。假定形變后船體梁為二次曲線，艏、舯、艉處3點與水線的交點坐標分別為(xa,da)、(xm,dm)、(xf,df)。其中：x為船長方向坐標，#0為原點；d為吃水值，基線為0；a、m、f分別對應艉、舯、艏3處。將3個點坐標值代入二次曲線方程求解。

設二次曲線方程為

d=a·x2+b·x+c

(1)

將坐標點代入式(1)中。

(2)

兩兩相減得

(3)

(4)

求解系數a和b。

(5)

(6)

得到系數a和b的表達式后，船長上每一點的吃水值都可以根據方程求得。在考慮艙室液面的實際縱傾時，對于規則艙室只需要考慮最前端與最后端處吃水差值，結合艙室的長度液面的傾斜角度就可計算求得，此數據代表液面的實際傾斜情況，是計算的關鍵。通過假定艙室前后壁的實際位置，即可推算出前后端壁處對應的實際吃水值，即此時該艙內液面傾斜狀態。

2.3 縱傾計算

設目標燃油艙前后壁距#0距離分別為x1和x2,見圖1。

圖1 縱傾計算示例

將x1、x2代入方程中，求取實際對應吃水值。

(7)

此時該燃油艙傾斜角度為

(8)

此角度代表了艙室中液面的實際傾斜角度，如需要在測深表中使用，則需將此角度對應的轉換到假定無形變時，該液面狀態對應的船舶假定縱傾值。

如圖1所示，假定船舶不發生形變，燃油艙實際液面保持不變，此時的液面即為不發生形變時的水線面，取水線面與艏艉柱的交點即為不發生形變狀態下的艏艉柱吃水，二者相減即可得到該燃油艙液面對應不發生形變時的船舶縱傾值，亦即可以在測深表中直接使用的計算縱傾值。

使用公式可以求出該縱傾值為

dtrim=(df-da)+[(xa+xf)-(x1+x2)]·

(9)

由此公式可精確求出某艙室液面對應的計算縱傾值。在實際應用中，根據船舶已有數據可將此公式簡化，便于運用。在吃水已知的情況下，由上式知修正縱傾的計算公式僅與艙室的實際位置有關，若艙室的實際位置確定，其在不同吃水下對應的實際縱傾也相應的確定下來。

2.4 實船應用

實船根據液位遙測位置的不同公式由不同程度的簡化。

2.4.1 當液位遙測位置處于垂線處時

此時讀取的首、尾吃水與測深表中定義相同，可以直接參與計算。此時船舯為垂線間長的中點，公式可進一步簡化，即LPP=xa+xf=2xm，代入縱傾計算公式得到：

dtrim=(df-da)-

(10)

由此可知特定艙室內液面縱傾狀態可以簡單的通過首中尾吃水，以及艙室所在的位置決定，經過公式計算的縱傾值可直接用于測深表計算。

2.4.2 當首尾中吃水在其他位置時(吃水標志處或液位遙測裝置處)

此時需要知道吃水讀取處于垂線的距離，以將之轉換到對應垂線處。

設吃水標志與垂線處距離為：lf，lm，la(locality-perpendicular)，經過線性計算，得到對應垂線處的轉換公式。

(11)

式中：dfp,dmp,dap分別為轉換后的首、中、尾垂線處吃水。

將上述換算公式代入式(10)得：

dtrim=(df-da)[1-(lf-la)/(lpp-la+lf)+

(lpp-(x1+x2))/0.5lpp·(lf+la-2lm)/

(lpp-la+lf)]-(Lpp-(x1+x2))/

0.5lpp(da+df-2dm)

(12)

在提前輸入固定距離參數的情況下，此公式最終也能轉換為僅包含變化值首中尾吃水，以及艙室前后位置的簡單方程。由最終結果方程知，不論吃水是否在垂線處，均只需艙室前后端坐標以及首、中、尾3處吃水值即可計算出此吃水狀態下，該油艙實際傾斜狀態對應的計算縱傾值。使用此縱傾計算艙容，可以得出更精確的計算結果。在使用此公式簡化時，液位遙測所在位置決定了公式中的固定距離參數，這些固定參數均可在原理圖中找到。

3 實船驗證

前述實船保單中，根據該船實際尺度和油艙所在坐標，計算得到1號2號燃油艙實際縱傾計算公式。

NO.1 H.F.O：

Trim=1.102·(df-da)+0.856·(da+df-2dm)；

NO.2 H.F.O：

Trim=1.109·(df-da)+1.296·(da+df-2dm)。

使用此公式計算的縱傾值dtrim,到測深表中計算艙容，結果見表3、4。

表3 根據修正公式計算的卸貨前船舶狀態及燃油艙油量

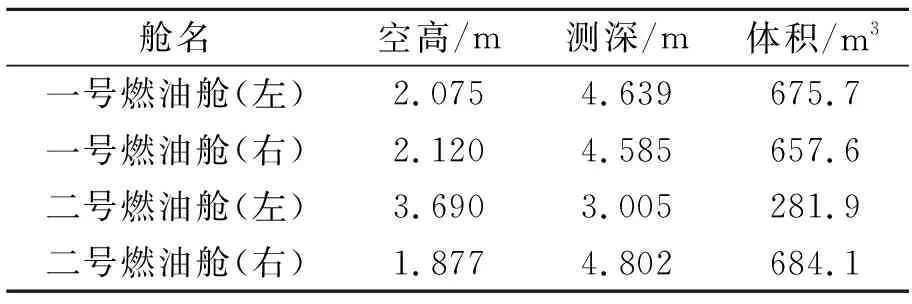
表4 根據修正公式計算的卸貨后船舶狀態及燃油艙油量

使用公式計算縱傾值，卸貨前總燃油量為2 293.3 m3，卸貨后則是2 299.3 m3，2種狀態下總艙容僅相差6 m3，證明了公式的準確性。

對比前后計算結果，使用首尾吃水縱傾計算艙容時因吃水狀態不同誤差也不同，在船舶處于中垂狀態時，計算結果會比實際結果偏小，因為在此情況下中吃水低于計算值，而相應的在船舶處于中拱狀態時，計算結果會比實際結果偏大。

前述保單中的較大誤差一部分原因是裝卸貨兩種情況恰好一為垂、一為中拱，才導致兩種狀態下總艙容相差較大。

當應用于實船時，往往會面臨實際燃油艙的形狀并不規則的情況。考慮到實際船舶運營時油量的計算多以油量計結果為準，艙容測算往往用作驗證手段，因此不需要太高的精度。若不規則油艙總容積較小，此時可以簡單視之為規則形狀來計算修正縱傾。因為縱傾值的微小誤差反饋到艙容計算時影響很小。若不規則油艙體積較大，則可根據其形狀分布將其以吃水高度為界限劃分為若干個規整的區域，在不同的吃水范圍時選用對應的縱傾修正公式，有助于更加精確的測算艙容[6]。由于實際計算時往往會忽略中拱中垂的影響，而中拱中垂的影響事實上不可忽略，當未慮及船舶實際狀態時，難免導致計算的誤差。這也是從業者在測深表輸出或者艙容測算時需要考慮的問題。

4 結論

1)通過曲線模擬得出的測深表縱傾修正公式，在代入實船數據驗證時結果與實際情況更為吻合，表明精確計算艙室的實際狀態能夠得到更加精確的修正結果，減少甚至消除中垂中拱對測深表的影響。

2)在處理燃油艙實際位置時，選取的是常用的規則燃油艙。當面對不規則的艙室形狀時，可以進一步將艙室結構細分，以獲得更準確的修正結果。

3)分析得到的縱傾修正公式，可以用于類似實船縱傾修正計算，以提升測深表使用精度。

4)實際船舶的形變狀態不能簡單地模擬為二次曲線，在不同的海況條件下，受風浪流的共同作用實際的形變情況更加復雜。若對艙室容積測量有更高的精度要求，則需要進一步擬合實際的形變情況。