基于ADE算法優化的木材單板染色全光譜配色模型研究

魏艷秀 管雪梅 李文峰 黃青龍

（東北林業大學機電工程學院，黑龍江 哈爾濱 150040）

木材材色是決定木制品價值的重要因素，為了提高木制品的裝飾作用和產品價值，對木材及木質材料進行適當的材色改進十分重要，通過染色技術改良劣質材、仿制優質材，從而全面提高木材的價值，滿足人們對色彩多樣性的需求。木材染色中一個十分重要環節就是配色，其對染色后木材的材色質量至關重要[1-2]。采用人工配色，其對配色人員的素質要求較高，既費時又難以適應現代工業生產的要求，且成本高、準確性差。有學者提出將計算機配色的方法用于木材染色中加快染料配方生成的速度，提高工作效率，節約成本[3]。然而，計算機配色技術為紡織業的配色而研制，利用庫貝爾卡?芒克理論對測得的顏色相關量進行計算，采用了大量的假設，自適應能力差，難于精確獲得木材染色這類影響因素較多，過程變化復雜的染色配方。近年來，有學者將神經元網絡等智能算法應用于木材染色計算機配色模型的建立中，取得了一定的效果[4]。但僅從標準觀察者與施照態條件下進行了配方的預測，染色木材單板存在的同色異譜現象亟待解決。

物體表面的光譜反射率是表征物體表面顏色的固有屬性，根據該原則，Stearns?Noechel光學模型在計算機配色應用中具有較高的配色精度，有效地解決了配色過程中存在的同色異譜現象。但由于在全光譜波段進行預測，方程組規模特別巨大，但在配色過程中染料組分的數量通常不超過5，導致染料配方預測模型是病態且超定的，無法獲得預測配方精確解。馬崇啟等[5]中針對混色紗線配色問題采用傳統的LS法對超定方程組進行求解，但隨著染料種類的增加以及光譜分辨率的提高，方程規模非常巨大，常規的解法會消耗大量的時間與內存，而且LS方法獲得的模糊度浮點解與真值相差較大，嚴重影響了預測精度[6]。宋叢威等[7]提出了一種基于主成分分析的快速降維算法求解印染行業中的線性超定方程組，雖然縮短了計算時間，但在主成分增多時會導致算法結果不穩定。隨著智能算法的興起，將差分進化算法（DE）應用于優化求解過程逐漸成為研究熱點。DE是一種基于優勝劣汰的自然選擇原理對種群中的個體進行淘汰和保留的算法，算法本身具有一定的自組織、自學習與自適應的特點，但也不可避免的存在陷入局部最優解和搜索停滯的問題[8]。本研究通過對DE的變異因子和交叉因子進行改進，提出了一種自適應差分進化算法，使其隨著迭代過程自適應變化，避免陷入局部最優解以及搜索停止問題，提高病態超定方程組解算精度，進而提高染色配方預測精度。

1 實驗材料和儀器

1.1 材料

選取水曲柳（Fraxinus mandshurica）單板為染色基材，購于黑龍江省哈爾濱市，氣干旋切制成規格為60 mm×40 mm×0.5 mm的單板，干燥至含水率8%。

木材染色染料：活性紅X?3B染料、活性黃X?RG染料、活性艷藍染料，購于黑龍江省哈爾濱市。染色滲透劑JFC、固色劑（無水碳酸鈉）、促染劑（無水乙酸）均購于北京化工廠，均為分析純。

根據郭明輝等[9]中的染色工藝選取單位濃度的活性紅X?3B染料、活性艷藍染料、活性黃X?RG染料制備單一染料組分染色材，水曲柳單板及單一染料組分染色單板如圖1所示。

圖 1 漂白水曲柳單板及單一組分染料染色單板Fig.1 Bleached veneer of ash and single component dyed veneer

標準樣的染色基材選用水曲柳單板，將活性紅X?3B染料、活性艷藍染料、活性黃X?RG染料按比例進行組合，共得到36組染色方案，去掉其中相同比例的28組染色方案后，采用余下的8組染色方案用來制備標準樣，染料比例如表1所示。

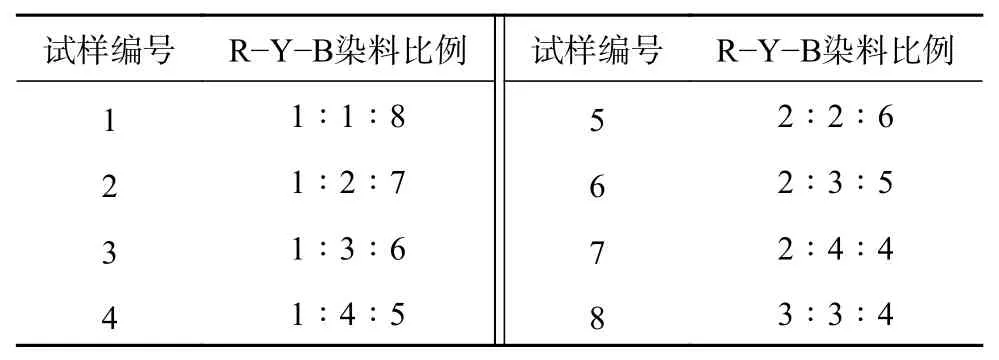
表 1 制備標準樣染料比例Table 1 Preparation of standard sample dye ratio

1.2 儀器

在顏色測量儀器選取中，通常采用RGB原理的彩色相機或分光光度計進行測量，但是彩色相機顏色感知精度較低，分光光度計雖具有較高的感知精度但僅能用于單點測量。高光譜成像技術具有高光譜分辨率，可實現成像與測譜同步進行。故本研究選用SPECIM高光譜成像工作站（SPECIM公司，芬蘭）進行顏色測量，其搭載VNIR?FX10相機，配備雙鹵素燈線性光源（400～2 500 nm）主要工作參數見表2。

表 2 SPECIM高光譜成像工作站工作參數Table 2 SPECIM hyperspectral imaging workstation operating parameters

SPECIM高光譜成像工作站將可見光近紅外光譜技術與高分辨率成像相結合，采用推掃式成像技術對實驗樣品進行逐線全波段光譜采集并同步生成圖像，圖像中每一像素點都記錄了其對應實驗樣品顏色信息的光譜特征，適用于對實驗樣品顏色特征進行定性、定量分析。SPECIM高光譜成像工作站工作方式如圖2所示。實驗中標準樣本對單點的光譜反射率進行3次測量取其平均值，單一組分染料染色材及擬合樣本在其正反面各取6點測量取其平均值，在400～700 nm波段內，步長5 nm進行取值，得到共61個波長下的光譜反射率。

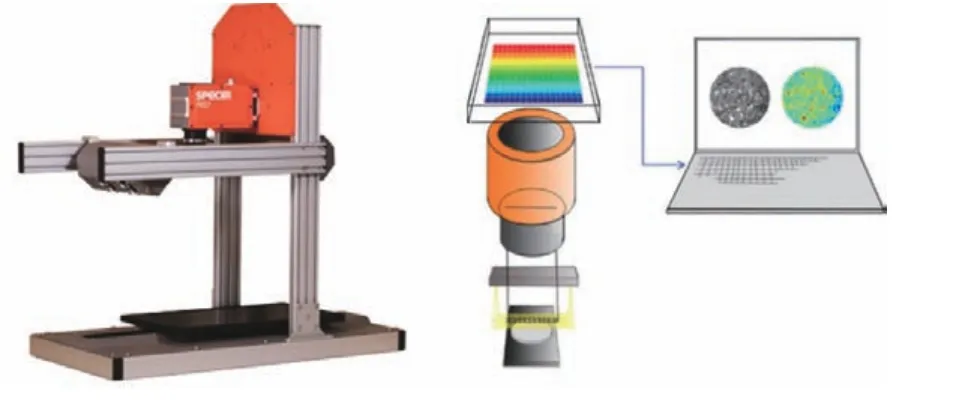
圖 2 SPECIM FX10高光譜成像工作站及其成像方式Fig.2 SPECIM FX10 hyperspectral imaging workstation and its imaging method

2 實驗模型與研究方法

2.1 Stearns?Noechel模型

木材單板染色計算機配色技術主要是研究多染料組分混合配色的光學模型和單一染料組分配比的配色算法。章斐燕等[10]通過單一組分的反射率與混合比例乘積的加和方法求出混合組分反射率的加和公式。但混合組分染料反射率和單一組分染料的配比關系是非線性的，在參考文獻[10]的

理論基礎上引入中間函數f[R(λ)]，使式（1）成立。

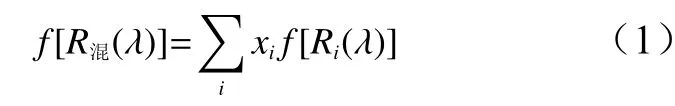
式中：R混(λ)表示波長為λ時混合染料染色單板的反射率；Ri(λ)表 示第i組分染料染色單板在波長為λ時的反射率；xi表 示第i組分染料在混合染料中的質量配比，實際生產中，xi應滿足

Stearns等[11]基于前人研究基礎，通過實驗驗證建立了混合組分反射率計算經驗公式，被稱為Stearns?Noechel模型，如式（2）所示

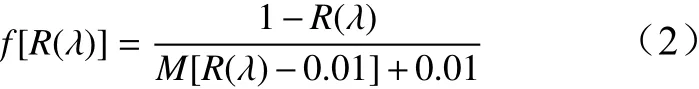
式中：根據Stearns等[11]的研究并結合木材單板染色特點，M為與染料性質和染色基材性質有關的可變常量；R(λ)表 示波長為λ 時的反射率。

根據式（2），可得出R(λ)與f[R(λ)]間的轉換關系如式（3）所示

木材染色單板反射光譜是唯一決定其表面顏色的因素。當前常用的計算機配色方法為三刺激值匹配法，但染色得到的擬合樣的反射光譜和標準樣并不一致，而是利用同色異譜理論進行配色的，所染單板在測色階段施照態和觀察者兩個角度與配色階段環境條件不符時，等色即被破壞，從而出現色差。為達到更高的染色品質，實現木材染色單板與標樣間的無條件匹配，根據參考文獻[2]中所提出的全光譜匹配方法，使標樣與擬合樣的光譜反射率完全相同，如式（4）所示。

選取活性紅X?3B、活性艷藍、活性黃X?RG3種染料求解染色配方xi，選擇波長400～700 nm波段，每間隔5 nm進行測量取值。根據式（1）、（4）可以得到式（5）～（6）。

其中，標準樣光譜反射率矩陣如式（7），擬合樣光譜反射率矩陣如式（8），單色染色單板光譜反射率矩陣如式（9），染料組分質量比例矩陣如式（10）。根據全光譜匹配定義，存在式（11）。由于在實際生產中，xi應滿足故需要對根據式（11）求得的染色配方進行歸一化處理，為滿足各組分質量比之和為1，如式（12）。歸一化后反射率滿足式（13）。

2.2 自適應差分進化算法優化全光譜配色模型

當λ=400,405,···,700時，根據線性代數理論，顯然式（6）沒有精確解，屬于超定方程組求解問題，本研究提出一種采用ADE算法求解超定方程組優化Stearns?Noechel模型，實現木材單板染色的全光譜配色。

DE的基本思路是，取2個個體之間的差分向量，將這個差分向量的1個加權形式加到第3個個體上從而產生1個新的候選解。DE由Storn等[12]提出，全局尋優能力強、收斂速度快并具有良好的魯棒性。DE的主要步驟如下：

1）設置種群規模N、最大進化代數（Max-Iter）、變異因子（F）和交叉因子（CR）等參數，初始化種群。

2）變異操作：隨機選出xr2和xr32個個體，其中r2≠r3，將這2個個體之間的差的伸縮形式加到第3個隨機選擇出的個體xr1中 ，r1?{r2,r3}。進而獲得1個可能被候選解種群接收的變異vi。

3）交叉操作：建立變異因子vi后，vi與1個差分進化個體xi交叉，得到試驗{向量ui，對于染色體j∈[1,n]，ui的第j個分量其中vij是vi的第j個分量，rcj是[0,1]上均勻分布的隨機數，jrand是[1,n]上均勻分布的1個隨機整數，xij是xi的 第j個分量。

4）選擇操作：在生成N個試驗向量ui后比較向量ui和xi， 在每對(ui,xi)中選擇適應性更強的向量作為差分進化的下一代。

通過對DE的分析與介紹可以得到算法流程圖如圖3所示。

在DE中，變異因子F和交叉因子CR的設置依賴于實際問題，通常情況下F∈[0.4,0.9]和 CR∈[0.1,1]，F的最優值一般與種群規模N的平方根成反比，CR的最優值一般隨著目標函數的可分離性減小[13]。交叉因子CR控制著ui的每一個分量來自變異向量vi的可能性，變異因子F決定了差分向量對變異向量的影響。當F與CR取值大時，全局搜索能力較強，取值小時，收斂速度較快，為權衡全局搜索能力與收斂速度，獲取最優算法性能。本研究采用自適應的變異因子和交叉因子改進DE，如式（15）所示。

式中：Ni表示當前迭代次數，Nmax表示最大迭代次數。自適應變異因子（F?）可以使算法在迭代前期具有良好的全局搜索能力，自適應交叉因子（ CR?）使算法在迭代后期快速收斂并具有更高的計算精度，保證了在超定方程求解過程中的計算效率與計算精度。

圖 3 DE流程圖Fig.3 DE algorithm flowchart

ADE具體步驟如下：

1）設置種群規模N、最大進化代數（Max-Iter），進行種群初始化。

NiNmax

2）判斷是否小于 ，是則進入循環，否則輸出最優解，記錄個體位置。

3）變異操作：采用如式（15）所示的自適應變異因子F?進行變異操作，在種群中隨機選出xr2和xr32個個體，其中r2≠r3，將這2個個體之間的差的伸縮形式加到第3個隨機選擇出的個體xr1中 ，r1?{r2,r3}。進而獲得1個可能被候選解種群接收的變異vi。

4）交叉操作：建立變異因子vi后，vi與1個差分進化個體xi交 叉，得到試驗{向量ui， 對于染色體j∈[1.n]，ui的第j個分量其中vi j是vi的第j個分量，rcj是[0,1]上均勻分布的隨機數，jrand是[1,n]上均勻分布的1個隨機整數，xij是xi的 第j個分量， CR?是自適應交叉因子。

5）選擇操作：在生成N個試驗向量ui后 比較向量ui和xi， 在每對(ui,xi)中選擇適應性更強的向量作為差分進化的下一代。

6）判斷全局最優解精度是否滿足要求，是則輸出結果，否則轉入步驟2）繼續執行。

通過對ADE算法的分析與介紹可以得到算法流程圖如圖4所示。

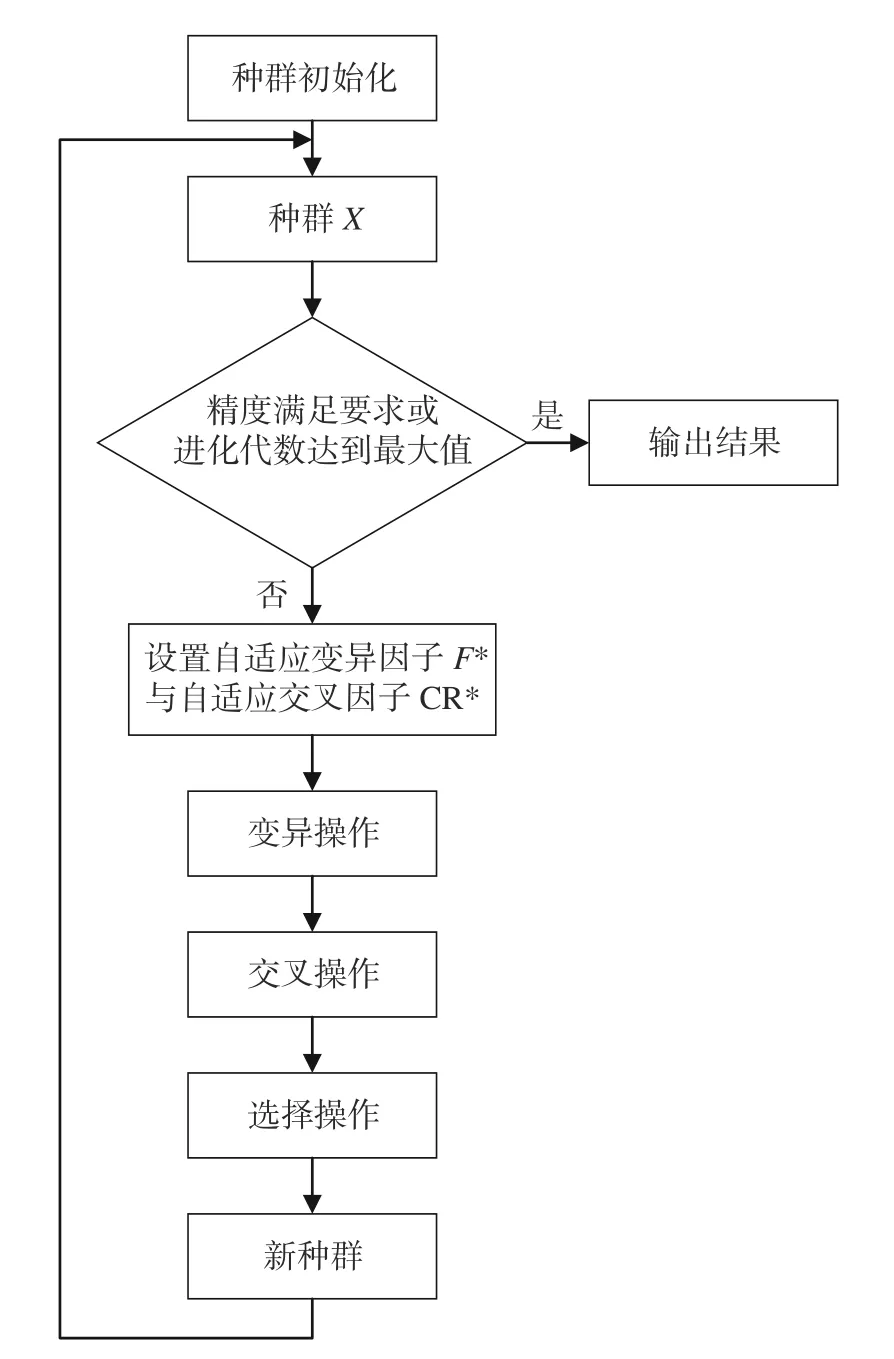
圖 4 ADE算法流程圖Fig.4 ADE algorithm flowchart

2.3 參數M最優值選取

M值作為Stearns?Noechel模型中的唯一可變參量，合理選取M值對達到標準樣與擬合樣顏色最優匹配具有重要意義。傳統選取M值的方法是已知混色樣品配方，將單組分樣品反射率以及質量分數代入Stearns?Noechel模型中反推M值，通過匹配實驗，選取所有試樣平均色差最小時的M值為最優值[14]。韓瑞葉等[15]和沈加加等[16]研究發現模型參數M與波長在部分波段存在線性相關，采用數據擬合的方法建立最優M值與波長的線性相關方程，增加了模型的預測能力，但采取這種方式的最優M值并不適用于所有的實驗樣本，依然對擬合樣的匹配造成了一定的誤差。本研究采用王泉等[17]提出的循環迭代取值方法求取最優M值，經過針對木材單板配色最優M值采用反推法進行多次實驗的基礎上，確定M通常取值范圍為[0,1]，設置初始值M0=0，步長為0.01循環迭代計算M值，選取色差最小時的M值作為最優M值，求得8組混合比例標準樣最小色差時的M值為0.21。

綜上，本研究提出的基于ADE算法優化Stearns?Noechel模型的單板染色全光譜配色過程見圖5。

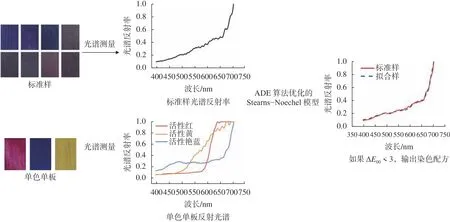
圖 5 基于ADE算法優化的木材單板染色全光譜配色過程Fig.5 Full-spectrum color matching process of wood veneer dyeing based on ADE algorithm

3 實驗結果與分析

為驗證本研究提出方法的有效性，根據以上流程設計實驗。采用SPECIM FX10高光譜成像工作站分別采集單組分染料染色單板及標準樣的反射光譜曲線如圖6所示。通過軟件ENVI 4.8在400～700 nm波段每隔5 nm進行取值，進而得到單色染色單板光譜反射率矩陣（F）與標準樣光譜反射率矩陣（F(Standand)），以標準樣1為例，采用ADE算法對式（6）進行求解。

圖 6 單色染色單板及標準樣的反射光譜曲線Fig.6 Reflectance spectrum curves of single component dyed veneers and standard samples

設置種群規模=50，最大迭代次數=100，傳統DE算法中，變異因子=0.5和交叉因子=0.9，ADE算法中變異因子及交叉因子按式（15）自適應選擇。

為保證實驗結果的可靠性，減少由于智能算法采用隨機搜索帶來的誤差，取100次優化結果平均值作為最終結果，并與LS法、GA算法、DE解算結果進行對比，以CIEDE2000色差（ ?E00）為解算精度評價標準，結果如表3所示。采用ADE優化全光譜配色模型對8組擬合樣染色配方進行預測，并根據預測結果進行擬合樣染色，預測配方及擬合樣與標準樣對比結果如表4所示。

根據表3，利用ADE求解染色配方得到的擬合樣與標準樣1的色差最小，與傳統的LS法、GA和基本DE相比，色差分別約為1/5、1/3、1/2。其中，利用LS法求解染色配方得到的擬合樣與標準樣1間的色差較大，產生的色差人眼可以分辨。

通過表4可以得出，8組實驗標準樣與擬合樣的明度差絕對值均值為1.15，擬合樣與標準樣明度相近，其中第1、4、6組明度差為負值，表明擬合樣顏色略深于標準樣，第2、3、5、7、8組明度差為正值，表明擬合樣顏色略淺于標準樣；8組實驗標準樣與擬合樣的彩度差絕對值均值為1.6875，擬合樣與標準樣顏色純度相近；8組實驗標準樣與擬合樣的色差均值為2.09，其中第4組擬合樣與標準樣的色差最大為2.9，第6組擬合樣與標準樣的色差最小為1.3，均滿足木材染色單板生產顏色質量要求。

表 3 標準樣1解算結果對比Table 3 Standard sample 1 solution comparison

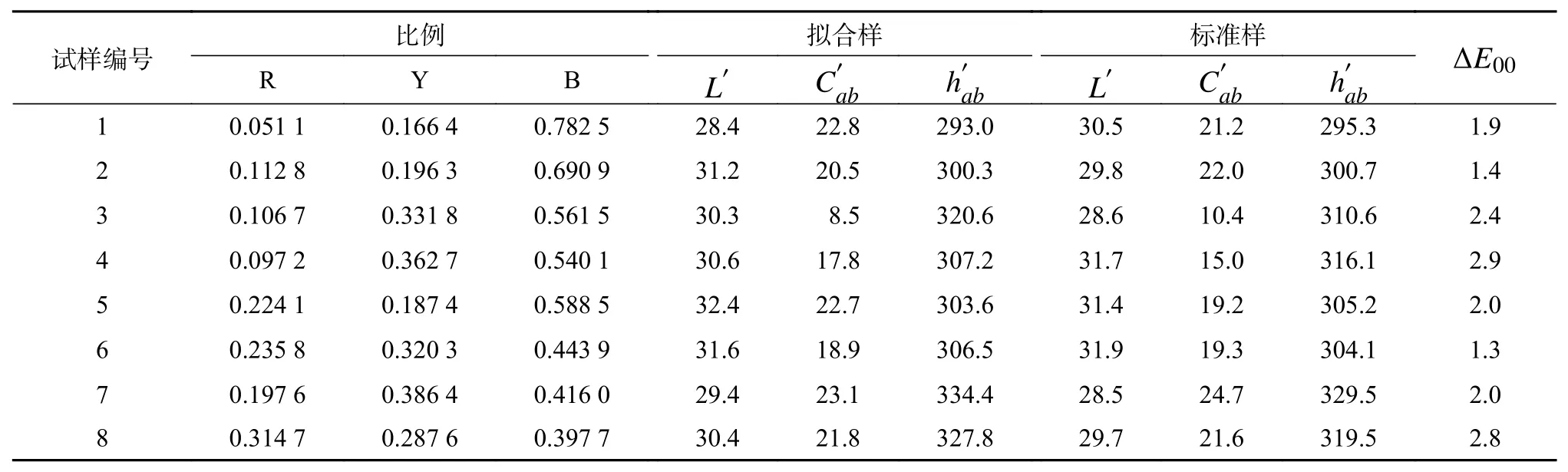
表 4 ADE優化全光譜配色模型預測結果Table 4 ADE optimized full-spectrum color matching model prediction results

基于Matlab 2016a平臺，分別使GA、DE、ADE迭代次數滿足搜索到最優解的要求，得到不同進行解算優化過程曲線如圖7所示。其中，GA迭代次數約為230，DE迭代次數約為60，ADE迭代次數約為30。可見基于ADE優化Stearns?Noechel模型的木材單板染色全光譜配色可以高效解算出精準的染色配方。

圖 7 不同算法優化過程曲線Fig.7 Different algorithm optimization process curves

4 結論

通過高光譜成像技術對染色木材單板進行反射光譜 采 集，采 用ADE優化Stearns?Noechel全光譜配色模型，并通過循環迭代法選取模型中M參數的最優值。將ADE的計算結果與其他優化算法的計算結果進行對比，可以看出，通過循環迭代法在[0,1]區間內確定染色木材單板配方預測模型中參數M的最優值為0.21。通過采用不同優化算法對標準樣1進行配方預測，LS、GA、DE和ADE預測配方得到的擬合樣與標準樣間的色差分別為11.7、6.3、3.9和1.9，結果表明，ADE優化模型得到的配方具有更高的預測精度。采用ADE優化模型對8組標準樣進行配方預測，得到擬合樣與標準樣色差分別為1.9、1.4、2.4、2.9、2.0、1.3、2.0、2.8，色差均小于3，顏色差異人眼不可辨識。GA與DE分別在迭代230次與60次時搜索到最優解，而ADE搜索到最優解的迭代次數僅為30次，結果表明，相同條件下，ADE的尋優效率更高。

綜上，基于ADE優化的染色木材單板全光譜配色模型可以有效地預測染色配方，且具有較高的計算效率與預測精度，滿足染色木材單板顏色質量要求。