高山松單木地上生物量模型不確定性研究

王柯人 舒清態 趙洪瑩 譚德宏 袁梓健

（西南林業大學林學院，云南 昆明 650233）

森林作為“地球之肺”，其生物量的估測、監測和評價一直是學術界的關注熱點，其中生物量估測的建模發揮著重要作用。國內外關于森林地上生物量估算的方法眾多：基于單木水平生物量模型構建[1-2]、基于林分生物量模型構建[3-5]。在建立單木地上生物量模型時，為評價模型擬合優度，國內外學者采用確定系數（R2）、估計值的標準差（SEE）、平均系統誤差（MSE）及總相對誤差（TRE）等[6]。

關于單木地上生物量模型建立過程中的不確定性來源一般分為三方面：抽樣誤差、模型誤差和測量誤差[7]。Shettles等[8]認為，模型誤差在3種誤差來源中所占比重最大。鑒于此，本研究重點為模型誤差的分析。模型誤差來源分為四方面：變量本身的誤差、殘差變異性、參數估計產生的誤差、所選擇模型的誤差[9-10]。當前國內外關于模型的誤差分析集中于多個模型精度評價和比較[1,11-12]，變量本身的誤差分析，也就是測量過程中誤差分析[13-14]，關于模型參數不確定性及殘差變異性分析常被忽略。王仲鋒等[15]認為采用非線性最小二乘回歸法求解單木地上生物量冪函數的參數及參數協方差矩陣，可獲得較高精度，對模型參數不確定進行分析。傅煜等[16-17]認為對于非線性模型，運用泰勒級數一階展開項度量非線性模型的參數誤差可以取得較好的效果。如何計算量化多種多樣的不確定性以提高森林地上生物量估算的精確度已成為當前研究的重要挑戰。

本研究以云南省香格里拉市為研究區，基于香格里拉市2016年森林資源二類調查數據，通過建立一元、二元地上生物量模型來估算高山松（Pinus densata）單木地上生物量[18-19]，并分析了2種模型的不確定性，以期為提高高山松森林地上生物量估測精度提供參考。

1 研究區概況

香格里拉市位于云南省西北部（99°23′06.08″～

100°18′29.15″E，26°52′11.44″～28°50′59.57″N），總面積114.2萬hm2，東、南、西三面被金沙江環繞，是滇、川、藏三省區交界地，也是世界自然遺產“三江并流”景區所在地。主要地貌類型為山地，地形總趨勢西北高、東南低，海拔為1 503～5 545 m。區域內高山松作為我國西南部香格里拉地區及青藏高原地區的特有森林建群種，起源于油松（Pinus tabuliformis）與云南松（Pinus yunnanensis）的天然同倍體雜種，在高山地區形成大面積純林，對保持高原森林生態環境有十分重要的意義[19]。

2 材料與方法

2.1 高山松單木數據

研究所使用的113株高山松地上部分生物量數據通過收獲法獲取，并測量單木胸徑（DBH）、樹高（H）以及木材、樹皮、樹枝及樹葉鮮質量，分別抽樣帶回實驗室，在85 ℃下恒溫烘干至恒質量，稱量樣本干質量，換算得出樣木各組分干質量，匯總得出立木地上生物量。高山松單木建模數據統計特征見表1。單木各部分生物量數據中，單木胸徑在每個徑階分布不均，單木地上生物量最大值為2 058.5 kg，最小值為4.03 kg。單木各個部分生物量平均值及標準差差異顯著，干材生物量平均值及標準差最高，樹葉生物量平均值及標準差最低。

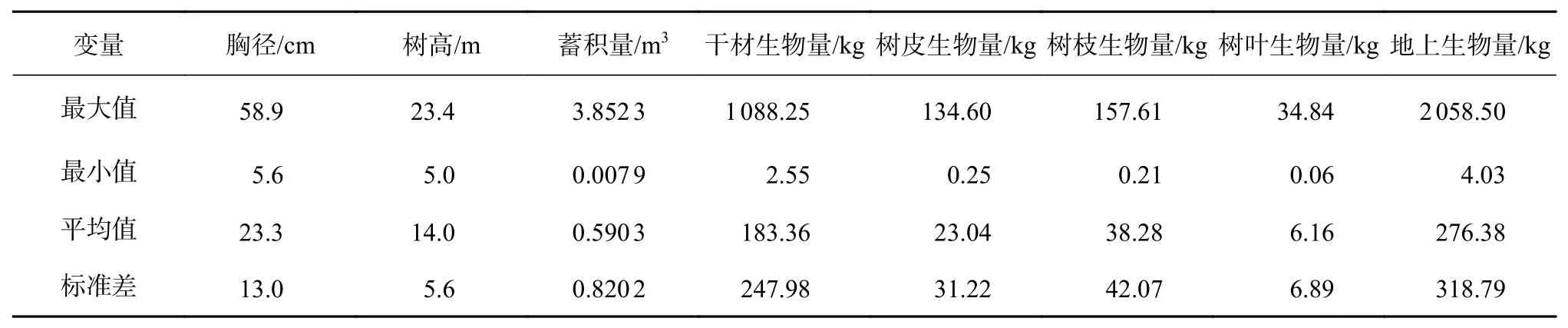
表 1 高山松單木建模數據統計特征Table 1 Statistical characteristics of modelling data sets

2.2 生物量模型的構建

已有研究表明，冪函數在針葉林生物量模型構建中效果較好[1-3]。本研究基于冪函數進行高山松單木地上生物量模型構建，分別采用胸徑單變量和胸徑?樹高進行擬合，并采用最小二乘法求解公式中的參數采用最小二乘法求解公式中的參數，計算公式由式（1）、（2）表示。

2.3 模型誤差變異不確定性分析

回歸模型建立過程中，利用殘差值表示回歸分析中測量值與方程預測值的差值來反映生物量模型擬合的效果[18]，如式（1）、（2），則模型誤差可表示為：

研究發現，殘差的標準差隨單木地上生物量的增加而增加，呈線性關系[9]。即：

式中：μ為殘差值的標準差，β為擬合參數。

在計算μ時，本研究采用六步法計算[20]，將單木地上生物量的實測值AGB進行升序排列，計算預測值及殘差值ε，再以n個樣本為一組，若最后一組不足n，則計入上一組，n取5、8、10。最后計算每組數據生物量預測值的平均值及殘差的標準差με，此時，對于生物量預測值的平均值、殘差值的標準差和擬合參數可通過下式計算：

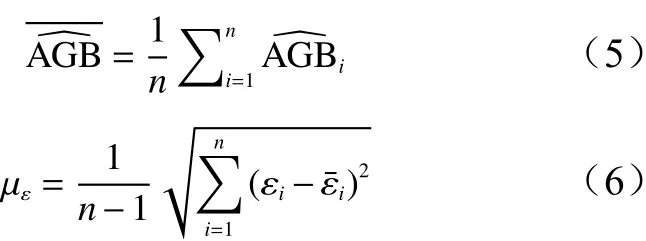
2.4 模型參數對生物量模型估計不確定性分析

采用非線性最小二乘法的原理求解單木高山松地上生物量模型參數a、b、c。參數引起的不確定性，可以采用泰勒級數對式（1）、式（2）展開[9-10,16]。則有：

式中： AGBi(x,γ)中參數γ可反映最近似真實值的

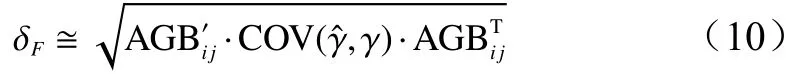
2.5 模型不確定性合成

模型誤差指在生物量模型估計中的誤差，其中最主要的是模型殘差變異不確定性和模型參數估測誤差。由已有研究可知，生物量模型估測中不確定性來源于抽樣誤差和單木生物量外推時傳播并累計下來的誤差，并具有傳遞性[17,21-22]。因此高山松單木地上生物量估測模型綜合不確定性（ξ）可通過模型殘差變異性和模型參數估測誤差來表示：

式中：β為模型殘差不確定值，δF為地上生物量模型參數引起的模型估測誤差。

3 結果與分析

3.1 生物量模型評價

本研究以高山松單木胸徑以及樹高和胸徑組合分別構建一元和二元回歸模型，結果見表2。由表2可知，2個模型回歸系數以及調整后的回歸系數（Radj2）均大于0.9，說明模型擬合效果較好；二元地上生物量模型調整回歸系數、均方根誤差（RMSE）均優于一元地上生物量模型。根據生物量建模數據繪制單木地上生物量、胸徑及樹高散點圖見圖1～2。由圖1可知，高山松單木建模數據集中于胸徑0～30 cm，高山松胸徑小于20 cm時，地上生物量增長緩慢，當胸徑大于30 cm，地上生物量呈上升狀態，且增長速率增大。由圖2可知，單木樹高、胸徑和地上生物量呈明顯的線性關系。

表 2 單木生物量模型的構建Table 2 Construction of individual biomass model

圖 1 高山松一元地上生物量模型Fig.1 Univariate biomass model ofP. densata

圖 2 高山松二元地上生物量模型Fig.2 Binary biomass model ofP. densata

3.2 一元地上生物量模型的不確定性分析

3.2.1 模型的殘差變異不確定性分析

根據模型殘差標準差與預測值的散點圖（圖3），一元單木地上生物量模型殘差變異引起的不確定性可表示為：0.615。對于一元地上生物量模型，由模型殘差變異引起的不確定性約為6.20%。

圖 3 殘差值的標準差與高山松生物量預測值的關系Fig.3 The relationship between the SD of the residuals and biomass prediction

3.2.2 模型參數對生物量模型估計不確定性分析

一元地上生物量模型參數對生物量模型估計的不確定性在MATLAB下將一元地上生物量回歸模型經過泰勒級數展開后求得靈敏度系數矩陣，也就是參數的協方差矩陣，可求得參數不確定性。其中，一元模型參數的協方差矩陣為可求得一元模型中由于模型參數帶來的不確定性δ=30.20%。根據殘差變異不確定性及參數不確定性進行不確定性合成，因此高山松單木一元地上生物量模型的綜合不確定性約為30.83%。

3.3 二元地上生物量模型的不確定性分析

3.3.1 模型的殘差變異不確定性分析

根據二元模型殘差值的標準差與預測值的變化，由圖4可知，從圖中可看出殘差值的標準差隨著單木地上生物量預測的增加而增加，與一元地上生物量模型的殘差標準差與單木地上生物量變化的趨勢相同。其變化規律可表示為：因此對于二元地上生物量模型而言，由模型殘差變異引起的不確定性約為5.17%。

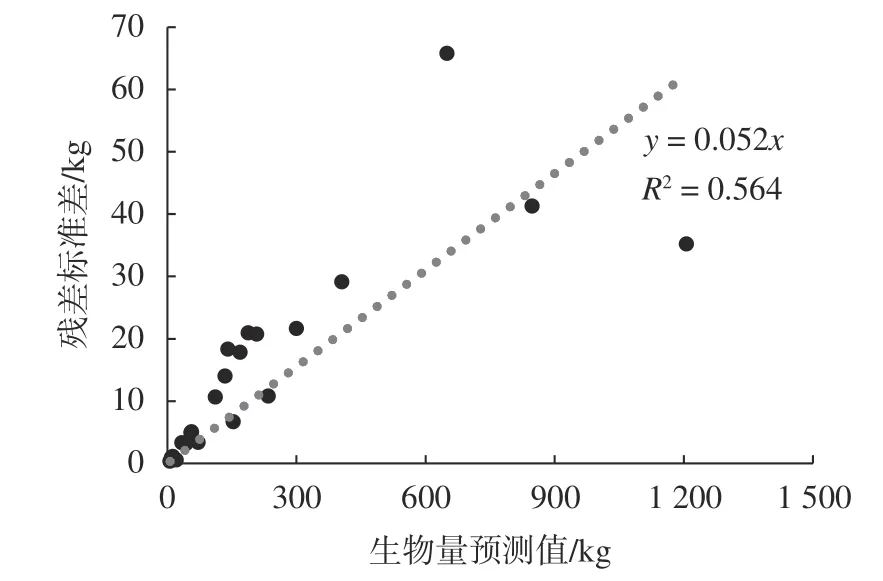
圖 4 殘差的標準差與高山松生物量預測值的關系Fig.4 The relationship between the SD of the residuals and biomass prediction

3.3.2 模型參數對生物量模型估計不確定性分析

將二元地上生物量回歸模型經過泰勒級數展開后求得靈敏度系數矩陣得到二元模型參數的協方差矩陣可

求得二元地上生物量模型的參數不確定性δ=3.12%。根據參數不確定性進行不確定性及殘差變異不確定性合成，因此高山松單木二元地上生物量模型的綜合不確定性約為6.04%。

3.4 建模樣木數量及分組方式對模型不確定性的影響

由于建模樣本數量一定程度反映了模型的適應性和可拓展性，本研究使用了113株樣木數據建模，為探究建模樣本數對模型構建的影響，本研究總樣本數（N）為113，隨機抽取了N/3、2N/3的樣本量，計算不同樣本量條件下的模型參數不確定性。其次，對比相關研究來看，不同分組樣本數對模型殘差的不確定性也有一定影響，為探究不同分組數據對模型殘差變異的影響，本研究還探討了5株一組、8株一組、10株一組的分組方式進行殘差不確定性變化分析，結果見表3。

表 3 不同建模樣木數量及分組方式對模型不確定性影響Table 3 Model uncertainty influence of different modeling sample quantity and grouping methods

由表3可知，當分組樣本數為5時，二元地上生物量模型的殘差變異不確定性、參數不確定性及綜合不確定性均優于一元模型，且模型參數引起的不確定性大于模型殘差變異不確定性。基于113株高山松單木生物量構建一元地上生物量模型中由模型參數引起的不確定性為30.30%，模型殘差變異引起的不確定性約為5.17%，綜合不確定性約為30.83%；二元回歸模型中由模型參數不確定性為3.12%，殘差變異引起的不確定性約為6.18%，綜合不確定性約為6.94%；隨著樣本量的增加，模型的參數不確定性及殘差變異不確定性逐漸減小，當建模樣本量從38增加至71時，模型的不確定性變化顯著，一元模型的參數不確定性和殘差變異不確定分別由49.89%和7.58%降低至35.39%和6.33%，綜合不確定性減少14.52%；二元模型參數不確定性和殘差變異不確定分別由41.47%和12.06%降低至5.82%和6.26%，綜合不確定性減少34.96%；當樣本數量大于71以后，模型不確定變化逐漸減小。分析得出一元地上生物量模型由單一變量構建，沒有考慮到樹高對于生物量估測的影響，因此一元地上生物量模型參數誤差引起的不確定性顯著高于二元地上生物量模型。

上述結果表明隨著樣本量的增加，模型的殘差變異不確定性逐漸減小；同時，隨著分組樣本數的增加，無論一元地上生物量模型和二元地上生物量模型，其模型的殘差變異不確定性也逐漸減小，雖呈現出一定的規律，但差異并不是很明顯，當分組樣本數分別為5株一組、8株一組、10株一組，一元地上生物量模型殘差變異不確定性分別為6.20%、4.85%、4.10%，二元地上生物量模型殘差變異不確定性分別為6.18%、4.81%、4.09%。分析得出，樣本數量較少時，分組的數量對于模型殘差變異不確定性有所影響，但影響較小，在計算模型殘差變異不確定性進行分組時應考慮樣本總量。

4 結論與討論

本研究基于113株香格里拉高山松單木地上生物量實測數據建立一元、二元地上生物量模型，并通過六步法計算模型殘差變異不確定性，泰勒級數展開式對模型參數不確定性進行計算，進行模型的參數及殘差變異的不確定性量化。通過分析得出以下結論：

1）二元地上生物量模型的殘差變異不確定性、參數不確定性及綜合不確定性均優于一元模型，且模型參數引起的不確定性大于模型殘差變異不確定性，隨著樣本量的增加，模型的參數不確定性及殘差變異不確定性逐漸減小，當樣本數為113時，生物量模型的不確定性最小。

2）隨著分組樣本數的增加，無論一元地上生物量模型和二元地上生物量模型，其模型的殘差變異不確定性也逐漸減小。

3）模型殘差變異不確定性和參數不確定性是單木地上生物量模型構建中不確定性的主要來源，增加模型參量能有效降低單木地上生物量模型中參數引起的不確定性。

本研究所使用的單木建模數據來源于香格里拉2個高山松天然林樣地，單木胸徑范圍為5.6～58.9 cm，胸徑均值為23.3 cm，標準差為13.03 cm，單木胸徑在每個徑階分布不均。在計算一元、二元模型殘差變異不確定時，當單株預測生物量介于500～1 500 kg時，殘差的標準差值產生較大波動，對殘差變異不確定性計算產生較大影響。本研究結果中的參數誤差引起的不確定性高于傅煜等[16,22]、Chen等[23]的研究，其原因主要為傅煜等使用了150株杉木作為建模樣本，并在模型分析法中引入了Monte Carlo法對模型進行了1 000次模擬，其有效降低了參數協方差矩陣的變異性，對參數殘差引起的不確定性度量更為準確；Chen等[23]采用了4 004株樣木進行建模，遠高于本研究，說明當樣本量足夠大時，參數誤差引起的不確定性趨近于零；其次，本研究基于113株高山松為樣本對高山松地上生物量估算不確定性分析，并在此基礎選取了總樣本量的1/3、2/3進行對比分析，可看出當建模樣本量從38增加至71時，模型的綜合不確定性變化顯著，而當建模樣本數量大于71以后，模型的綜合不確定變化趨于平緩。說明樣本量的增加能顯著降低模型殘差變異不確定性，參數不確定性以及模型綜合不確定性，該結果與秦立厚等[9,21]的研究結果一致，但建模最優樣本量還待今后進一步分析。

模型誤差來源分為四個方面，其中變量本身的誤差和所選擇模型的誤差已有較多研究。趙平安等[13]基于臨安市森林資源清查樣地數據和臨時樣地調查數據得出對于地上碳儲估算，誤差占比最大的為抽樣誤差和遙感影像坐標校正定位誤差。曾偉生等[24]的研究基于150株落葉松和馬尾松的立木生物量實測數據，對地下生物量模型的一元、二元回歸模型方案進行對比分析，得到馬尾松地下生物量模型估測精度可達90%以上，落葉松可達85%以上。本研究僅對殘差變異性和參數估計產生的誤差進行了計算，未對另外兩方面進行分析，今后還需進一步研究。