非緊致氣動噪聲半空間傳播基本解的邊界積分方法

錢振昊，賀 菲，劉秋洪

(西北工業(yè)大學(xué) 翼型葉柵空氣動力學(xué)重點實驗室，西安 710072)

0 引 言

聲比擬理論在低馬赫數(shù)流動氣動噪聲預(yù)測中應(yīng)用廣泛[1-2]。當固體邊界靜止且剛性時，頻域聲學(xué)積分方程為[3]：

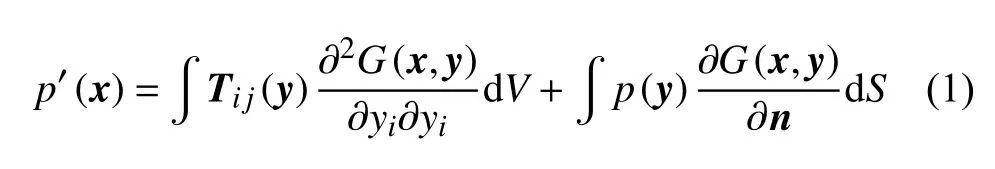
其中，p′為聲壓，p表示單位面積固體表面作用在流體上的力，Ti j為Lighthill應(yīng)力張量，x和y分別是觀察點和聲源，n為邊界的外法線方向，G(x,y)為格林函數(shù)。如果格林函數(shù)G(x,y)滿足邊界條件：

那么方程(1)可簡寫為[4]：

這種滿足聲學(xué)邊界條件的格林函數(shù)稱為精確格林函數(shù)，是聲波在空間傳播的基本解，包含非緊致邊界（邊界的幾何特征尺寸不是遠小于聲波波長）的聲散射，從而有效簡化氣動聲源的聲學(xué)建模。通過理論解析可得到簡單幾何結(jié)構(gòu)的精確格林函數(shù)，而對復(fù)雜非緊致邊界，精確格林函數(shù)需采用數(shù)值方法獲得[5-7]。

低馬赫數(shù)流動噪聲在半空間內(nèi)的傳播是氣動聲學(xué)領(lǐng)域的一個典型問題。若采用方程（3）進行噪聲預(yù)測，就必須獲得聲波在半空間傳播的基本解。當半空間邊界為聲學(xué)硬邊界時，一般采用半空間格林函數(shù)[8]和邊界元方法獲取聲傳播基本解。在此基礎(chǔ)上，利用Weyl-van der Pol公式[9-10]還可進一步得到阻抗半空間邊界聲散射的基本解，但這僅是一個工程近似處理方法。結(jié)合鏡像源方法、等效源原理和邊界元方法可得半空間阻抗邊界聲散射的基本解[11]，但需要處理奇異積分。Ochmann[12]提出復(fù)等效源方法以避免奇異積分，并采用邊界元方法計算了靜止均勻介質(zhì)中三維球體聲散射的基本解[13]。需要指出的是，Ochmann并沒有采用可靠算例驗證復(fù)等效源方法的正確性。

本文基于等效源方法，建立半空間二維圓柱聲散射基本解的理論模型，用以驗證復(fù)等效源方法的可靠性，并采用邊界積分方法獲得低馬赫數(shù)流動氣動噪聲在半空間傳播的基本解，考慮了均勻運動介質(zhì)對聲傳播的影響，為復(fù)雜物理問題的工程數(shù)值解提供理論支持。

1 復(fù)等效源方法與邊界積分方程

如圖1（a）所示，半空間內(nèi)y(y1,y2)點有一圓頻率為ω的單位強度簡諧單極子點聲源，x(x1,x2)為觀察點，聲場解用Gh0(x,y)表示。聲傳播控制方程為Helmholtz方程：

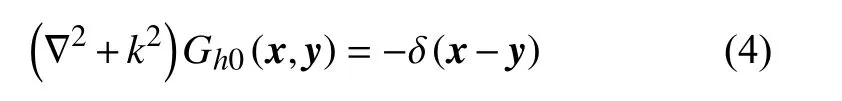
其中，c0為聲傳播速度，k=ω/c0為聲學(xué)波數(shù)。在半空間邊界處滿足邊界條件：

其中，nb為半空間邊界的外法線方向；γ為半空間邊界的聲學(xué)邊界條件參數(shù)，當γ=0時為聲學(xué)硬邊界；對阻抗邊界，一般Im(γ)＞0，Re(γ)＞0時為剛度型阻抗邊界，而Re(γ)＜0時為質(zhì)量型阻抗邊界。

采用鏡像源方法和復(fù)等效源原理考慮阻抗半空間邊界的聲散射問題，如圖1（b）所示。鏡像源和復(fù)等效源坐標分別為y′(y1,-y2)和ys(y1,-y2-si)，s∈[0,+∞)。假設(shè)聲場Gh0(x,y)具有如下形式：

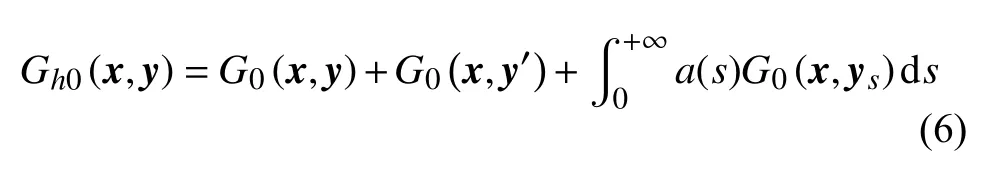
其中G0(x,y)、G0(x,y′)、G0(x,ys)分 別為點源y、鏡像點源y′和復(fù)等效點源ys的輻射聲場。

利用?/?nb=?/?x2，當觀察點位于半空間邊界上時x2=0，有G0(x,y)=G0(x,y′)，且有：

圖1 復(fù)等效源方法示意圖Fig. 1 Schematic of complex equivalent source method

將式（6、7）代入式（5），得到：

再利用關(guān)系式：

和分部積分，得：

如果a(s)G0(x,ys)|s=+∞→0，那么有：

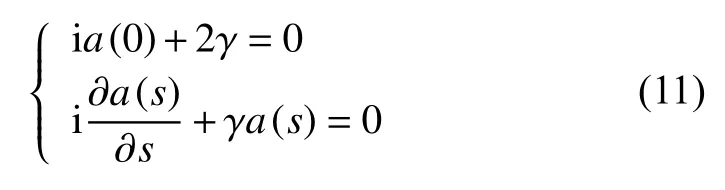
解得：

無論對質(zhì)量型半空間邊界Re(γ)＜0，還是對剛度型半空間邊界Re(γ)＞0有：

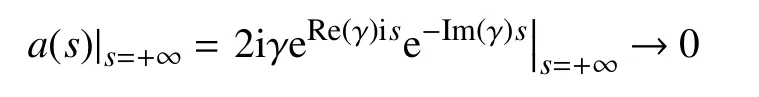
即a(s)G(x,ys)|s=+∞→0的假設(shè)是成立的。聲場的理論解為：

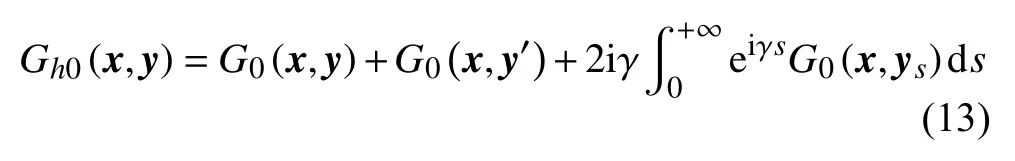
如果半空間中存在表面為S的剛性散射體，觀察點x處的聲場積分解用GN(x,y)表示，則有：

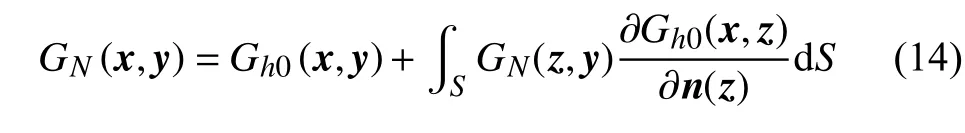
式中，n(z)為散射體表面z點的單位外法線。采用方程（14）不需要離散鏡像散射邊界，只需在離散散射邊界的基礎(chǔ)上，先將觀察點置于散射表面z點，采用邊界元方法求得邊界上的聲場GN(z,y)，然后再積分計算觀察點的聲場GN(x,y)。

對于二維問題，假設(shè)介質(zhì)均勻，且沿x軸方向以馬赫數(shù)Ma運動，自由空間格林函數(shù)G0(x,y)可表示為：

式中，i 為虛數(shù)單位，H0為零階第一類Hankel函數(shù)，

2 半空間圓柱聲散射理論解

如圖2所示，全空間中有兩個半徑為a的二維剛性圓柱C1和C2，圓心O1和分O2別位于x軸上下距離為h/2處，圓頻率為ω的單位強度簡諧單極子點源位于y點，x為觀察點。以O(shè)1為原點建立極坐標系，聲源點和觀察點坐標分別為(r1y,θ1y)和(r1x,θ1x)；以O(shè)2為原點建立極坐標系，聲源點和觀察點坐標分別為(r2y,θ2y)和(r2x,θ2x)。產(chǎn)生的用Gh(x,y)表示：

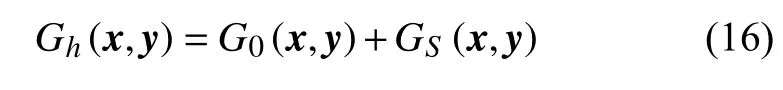
其中G0(x,y)和GS(x,y)分別為聲源聲輻射和圓柱聲散射。對于二維問題，假設(shè)介質(zhì)靜止均勻，有：

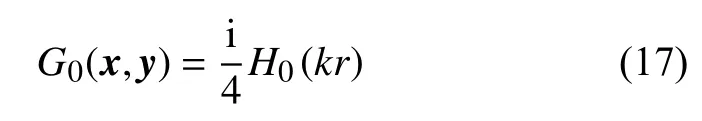
其中r=|x-y|。 圓柱C1和C2的聲散射用gs1(x,y)和gs2(x,y)表示，并假設(shè)：

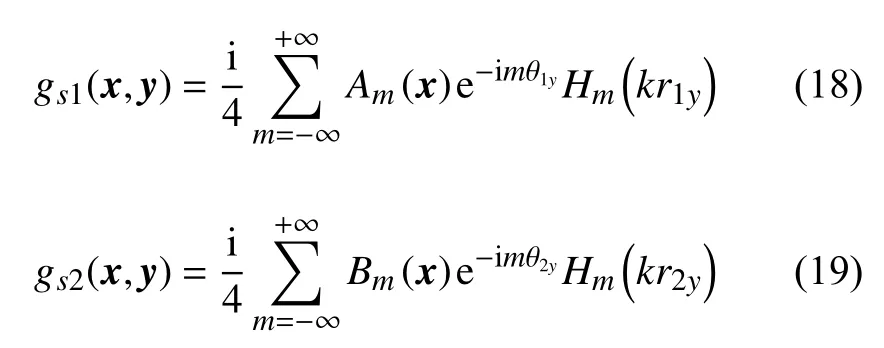
即GS(x,y)=gs1(x,y)+gs2(x,y)。Gh(x,y)在圓柱表面上滿足聲學(xué)硬邊界條件：

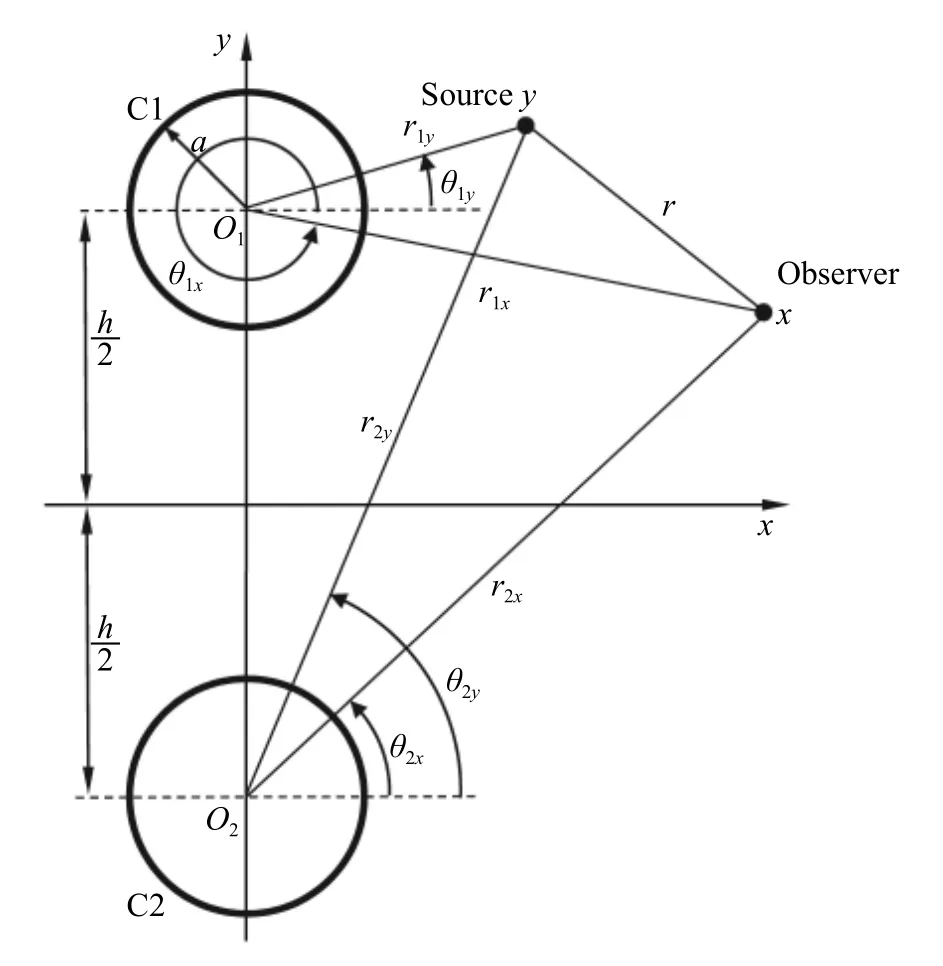
圖2 雙圓柱聲散射示意圖Fig. 2 Schematic of sound scattering from two cylinders

將源點置于圓柱C1表面，可得級數(shù)展開式：

式中，Jm和Hm分 別為m階Bessel函數(shù)和m階第一類Hankel函數(shù)。根據(jù)Graf加法定理[14]：

可得：

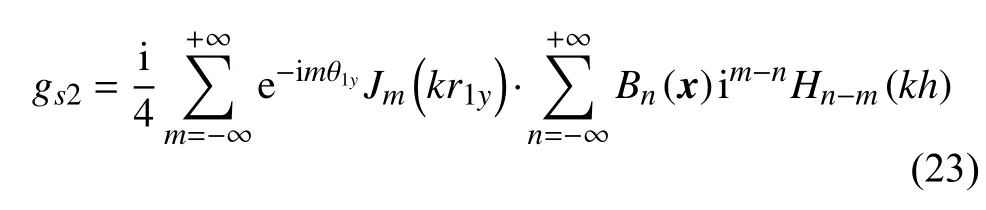
將式（18、21、23）代入邊界條件（20）即可得到：

將源點置于第二個圓柱 表面，可得：

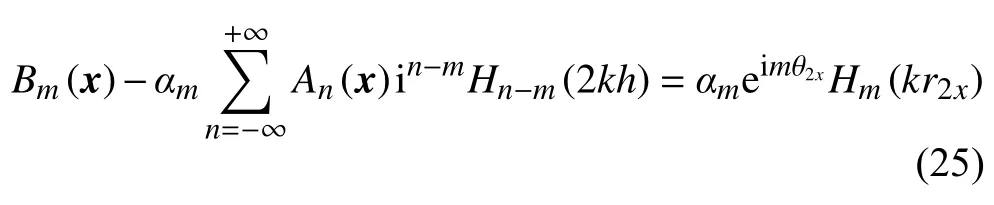
將方程(24、25)改寫為：

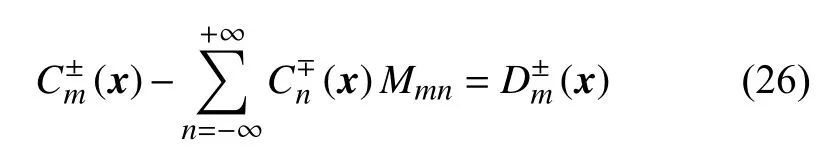
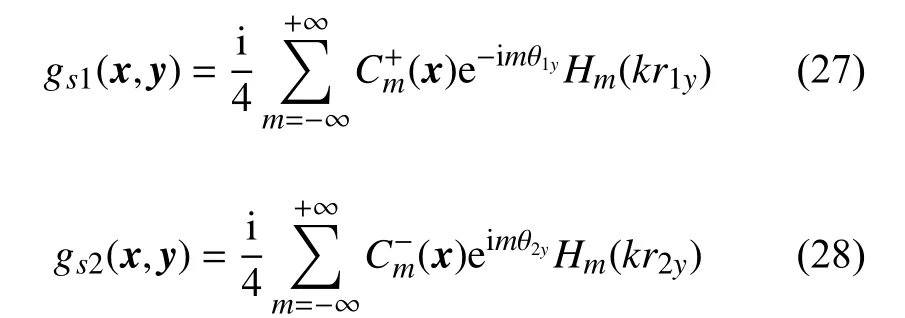
采用等效源方法將圖3（a）所示的半空間圓柱聲散射轉(zhuǎn)化為圖3（b）所示的全空間雙圓柱聲散射。對質(zhì)量型阻抗半空間邊界，鏡像源和等效源坐標分別為y′(y1,-y2)和ys(y1,-y2-s)，s∈[0,+∞)。觀察點聲場用GA(x,y)表示，仿照復(fù)等效源方法，可得等效源方法的結(jié)果為：

同理，對剛度型阻抗半空間邊界，有：

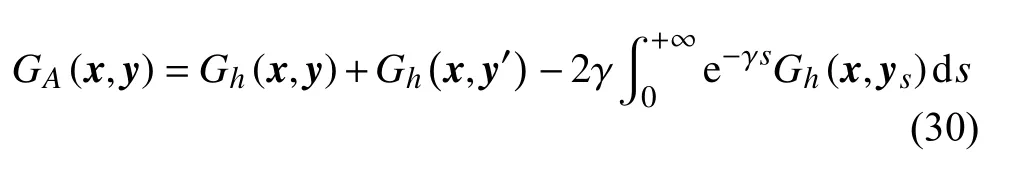
其中等效源坐標為ys(y1,-y2+s),s∈[0,+∞)。

圖3 等效源方法示意圖Fig. 3 Schematic of equivalent source method

3 算例驗證

如圖4所示，半徑a=0.05 m二維圓柱位于無窮大邊界上方h/2=2.0 m處，簡諧單極子點源與圓柱圓心位于同一水平位置，距離圓心d=0.1 m，觀察點分布在以圓柱圓心為中心、半徑為12.8 m的半圓上，其中P點坐標為 (256a,2)。對靜止均勻聲傳播介質(zhì)，理論計算過程中m取 值范圍為 [-50,50]以保證足夠截斷精度。有限區(qū)間數(shù)值積分采用四點Gauss-Legendre積分方法，半無窮區(qū)間數(shù)值積分采用五十點Gauss-Laguerre積分方法。

取γ=-5+5i， 此時半空間邊界為質(zhì)量型阻抗邊界。圖5是基于復(fù)等效源方法的邊界積分數(shù)值解|GN(x,y)|和 基于等效源方法的理論解 |GA(x,y)|在空間P點隨波數(shù)的變化圖。在各頻率下，復(fù)等效源方法和等效源方法的解吻合一致。

圖4 半空間圓柱聲散射算例示意圖Fig. 4 Schematic of the computational cases for sound scattering from a cylinder in half-space

圖5 質(zhì)量型平面上方剛性圓柱聲散射在P點隨波數(shù)的變化Fig. 5 Wave number dependence of sound scattering from a cylinder above a mass-like impedance plane at point P

波數(shù)為20時，點源輻射聲波的波長與圓柱直徑的比值約為3，圓柱聲學(xué)非緊致，聲散射的空間指向性分布如圖6所示。理論解與數(shù)值解在所有的觀察點處相吻合。對剛度型半空間邊界，取阻抗參數(shù)γ=5+5i。基于復(fù)等效源方法的數(shù)值解和基于等效源方法的理論解在不同波數(shù)和觀察點處仍然是一致的，這里不再贅述。

圖6 質(zhì)量型阻抗平面上方圓柱聲散射指向性分布圖Fig. 6 Acoustic directivities of sound scattering from a cylinder above a mass-like impedance plane

4 半空間聲傳播基本解

對直徑為D=0.1 m 的二維剛性圓柱，假設(shè)均勻無窮遠來流沿x軸方向，馬赫數(shù)Ma=0.2 ，雷諾數(shù)Re=9×104。文獻[15]對該流動進行了數(shù)值模擬，得到圓柱無量綱渦脫落頻率為St=0.235。圓柱繞流產(chǎn)生的噪聲主要集中在渦脫落頻率St=0.235及其一次諧波St=0.47上，分別為升力和阻力脈動對應(yīng)的頻率，聲波的波長λ與圓柱直徑D的比值分別約為24和12。

取P點為觀察點，假設(shè)介質(zhì)靜止均勻。不考慮圓柱邊界和半空間邊界對聲傳播的影響，認為聲波在全空間中自由傳播，格林函數(shù)虛部Im(G0(P,y))的空間分布如圖7所示。進一步考慮圓柱邊界的聲散射，精確格林函數(shù)虛部 Im(GN(P,y))的空間分布如圖8所示。當 λ/D≈24時，圓柱表面附近聲源輻射的聲波仍然呈現(xiàn)非緊致特性。

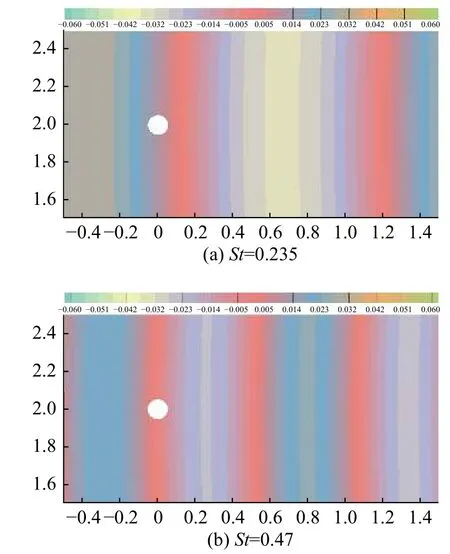
圖7 自由空間I m(GN(P,y))的空間分布Fig. 7 Distributions of I m(GN(P,y)) in free-space

從方程(3)可知，若氣動聲源Tij已知，噪聲計算的關(guān)鍵就在于獲得精確格林函數(shù)的空間二階偏導(dǎo)數(shù)。在精確格林函數(shù)數(shù)值解的基礎(chǔ)上，采用五點中心差分格式先求精確格林函數(shù)的空間一階偏導(dǎo)數(shù)，再求二階偏導(dǎo)數(shù)。圖9所示為精確格林函數(shù)二階混合偏導(dǎo)數(shù)虛部 Im(?2GN(P,y)/?y1?y2)的空間分布。

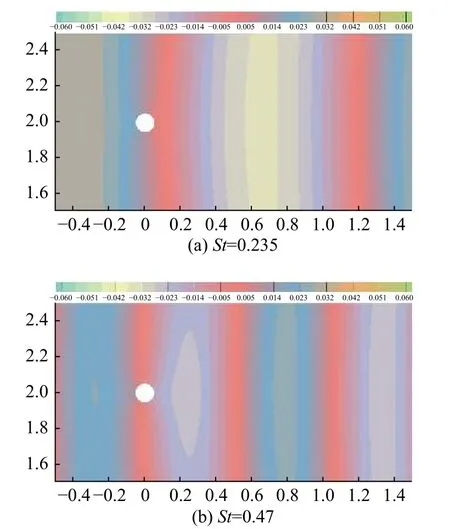
圖8 全空間I m(GN(P,y))的空間分布Fig. 8 Distributions of I m(GN(P,y)) in full-space

Im(?2GN(P,y)/?y1?y2)圖9 全空間 的空間分布Im(?2GN(P,y)/?y1?y2)Fig. 9 Distributions of in full-space

對圖4所示半空間圓柱，由于圓柱距離半空間邊界足夠遠，可忽略半空間邊界對流動的影響，認為無量綱渦脫落頻率仍為St=0.235。對質(zhì)量型半空間阻抗邊界取 γ=-5+5i， 對剛度型半空間阻抗邊界取γ=5+5i。半空間邊界分別為聲學(xué)硬邊界、質(zhì)量型阻抗邊界和剛度型阻抗邊界時，精確格林函數(shù)GN(P,y)的虛部在St=0.235處的空間分布如圖10所示。由于半空間邊界的散射作用，聲場的分布與圖8（a）相比存在很大不同。

圖10 半空間I m(GN(P,y))在在渦脫落頻率處的空間分布Fig. 10 Distributions of I m(GN(P,y)) at the vortex shedding frequency in half-space

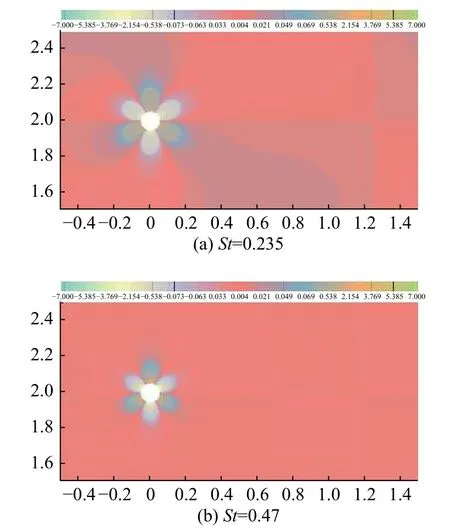
圖11為半空間邊界分別為聲學(xué)硬邊界、質(zhì)量型和剛度型阻抗邊界時，精確格林函數(shù)GN(P,y)虛部的空間二階混合偏導(dǎo)數(shù) Im(?2GN(P,y)/?y1?y2)在渦脫落頻率一次諧波St=0.47處的空間分布。與圖9（b）相比可清晰看出半空間邊界的存在強化了圓柱附近聲源的聲輻射能力。

考慮介質(zhì)運動對聲傳播的影響，取無窮遠來流的速度為均勻介質(zhì)的運動速度，即介質(zhì)運動馬赫數(shù)為Ma=0.2。觀察點P正好在來流的下游，介質(zhì)運動在這個方位上的影響最大。半空間邊界分別為硬邊界、質(zhì)量型和剛度型阻抗邊界時，精確格林函數(shù)虛部空間二階混合偏導(dǎo)數(shù) Im(?2GN(P,y)/?y1?y2)在渦脫落頻率一次諧波處的空間分布如圖12所示。與圖11相比可以發(fā)現(xiàn)此時介質(zhì)運動對聲場的影響比較小。圓柱繞流噪聲的主要聲源位于尾渦脫落區(qū)域，影響其噪聲輻射能力的主要是圓柱邊界的散射作用，而不是介質(zhì)運動的對流效應(yīng)。階混合偏導(dǎo)數(shù) Im(?2GN(P,y)/?y1?y2)在渦脫落頻率一

圖11 半空間I m(?2GN(P,y)/?y1?y2)在渦脫落頻率一次諧波處的空間分布Fig. 11 Distributions of I m(?2GN(P,y)/?y1?y2) at the first harmonic of vortex shedding frequency in half-space

圖12 介質(zhì)運動 Ma=0.2， 半空間I m(?2GN(P,y)/?y1?y2)在渦脫落頻率一次諧波處的空間分布Fig. 12 Distributions of I m(?2GN(P,y)/?y1?y2) at the first harmonic of vortex shedding frequency for the medium moving at Mach number 0.2 in half-space

圖13是半空間邊界為聲學(xué)硬邊界且介質(zhì)均勻運動馬赫數(shù)為0.25和0.3時精確格林函數(shù)虛部空間二次諧波處的空間分布圖。與圖11（a）對比可發(fā)現(xiàn)，當介質(zhì)均勻運動馬赫數(shù)超過0.2時，氣動聲源輻射的聲波特性會發(fā)生明顯改變。在這種情況下，必須考慮介質(zhì)運動的對流效應(yīng)。

圖13 介質(zhì)運動Ma=0.25,0.3，半空間硬邊界條件下Im(?2GN(P,y)/?y1?y2)在渦脫落頻率一次諧波處空間分布Fig. 13 Distributions of I m(?2GN(P,y)/?y1?y2) at the first harmonic of vortex shedding frequency for the medium moving at Mach number 0.25 and 0.3 in half-space with acoustic hard-wall boundary condition

5 結(jié) 論

基于復(fù)等效源方法，建立了半空間中非緊致聲傳播基本解的邊界積分方程，考慮了介質(zhì)均勻運動對聲傳播的影響。同時，利用等效源方法提出了一種半空間二維非緊致圓柱聲散射模型，推導(dǎo)了靜止介質(zhì)中聲散射基本解的理論表達式，驗證了邊界積分方程基本解的正確性。

對直徑0.1 m、無量綱渦脫落頻率St=0.235的二維圓柱繞流噪聲在半空間中傳播的基本解進行預(yù)估，重點研究了渦脫落頻率及其一次諧波聲源的聲輻射特性，結(jié)果顯示：1）圓柱對渦脫落頻率的聲波呈現(xiàn)明顯的非緊致特性；2）半空間邊界對聲傳播的影響顯著，能強化聲源的聲輻射能力；3）當流動馬赫數(shù)低于0.2時，介質(zhì)均勻運動對聲傳播的影響可以忽略。

盡管本文研究的是二維聲傳播問題，但復(fù)等效源方法對三維聲散射問題也是有效的。在后續(xù)工作中，我們將利用邊界積分方程的基本解對復(fù)雜結(jié)構(gòu)的氣動噪聲進行預(yù)測。