基于Simulink 軟件的組合滑模控制仿真實驗

趙海濱，田亞男

（1.東北大學 機械工程與自動化學院，遼寧 沈陽 110819；2.東北大學 信息科學與工程學院，遼寧 沈陽 110819）

滑模控制器具有響應速度快、對參數變化及擾動不靈敏和物理實現簡單等優點，廣泛用于非線性系統控制[1]。傳統的滑模控制器，穩態誤差不能在有限時間內收斂到零，從而提出了終端滑模控制的概念。終端滑模控制器能夠在有限時間內收斂到零，而且對建模不確定和外部干擾信號具有魯棒性。快速終端滑模控制器的收斂速度非常快，但是在接近平衡狀態時存在奇異問題[2]。本文將快速終端滑模控制器和線性滑模控制器相結合，設計了組合滑模控制器，并采用組合滑模控制器進行二階Duffing 混沌系統的平衡控制。

本文以二階Duffing 混沌系統為研究對象，采用組合滑模控制器進行系統的平衡控制，狀態變量快速收斂到零。采用Simulink 軟件建立仿真實驗系統進行仿真實驗，并對仿真結果進行分析。組合滑模控制器能夠進行不同初始狀態Duffing 混沌系統的平衡控制，能夠避免奇異問題，具有非常快的收斂速度。

1 二階非線性系統

二階Duffing 混沌系統常用于微弱信號的檢測[3]，是典型的二階非線性系統。對于Duffing 混沌系統的控制，已經提出很多方法[4-5]。Duffing 混沌系統的狀態方程表示為

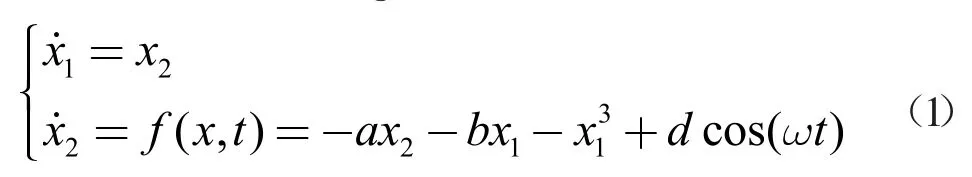
其中，x1和x2為系統的狀態變量，t 為時間，a、b、d 和ω 為常數。當a=0.4，b=-1.1，d=1.5，ω=1.7 時，該系統處于混沌狀態。

根據Duffing 混沌系統的狀態方程，采用Simulink 軟件進行仿真，采用變步長的ode45 算法，最大步長為0.001 秒。Duffing 混沌系統的初始狀態設定為x1（0）=0.2，x2（0）=0.3，系統的仿真時間設定為300 秒。……