600 MPa級配筋暖磚墻體的抗震性能研究

晁 崇，祝英杰

(青島理工大學 土木工程學院，青島 266033)

暖磚墻體全稱為承重框架保溫暖磚墻體，是一種新型承重復合墻，目的在于替代現有磚混結構承重墻，用在多層結構中.墻體外層為模具壓制成的EPS聚苯板，充當保溫層和砌筑模板，插入豎向鋼筋和水平鋼筋后向內部空腔澆筑混凝土，起承重和抗震作用.混凝土硬化后，一部分聚苯塊留在墻體中，由于聚苯塊強度很低，這部分可以視為孔洞.目前對于暖磚墻體的研究還不夠多，祝英杰等[1-2]對暖磚墻體進行了基本力學試驗，提出軸壓強度、抗剪強度、彈性模量及泊松比的確定方法，對高強鋼筋在暖磚墻體中的應用尚沒有研究.目前，國內對配置600 MPa級鋼筋的混凝土構件研究較少且多集中在混凝土梁和柱方面，對配置600 MPa級鋼筋的剪力墻的研究也不多.郭蓉等[3]通過對配置HRB600級鋼筋的剪力墻進行擬靜力試驗，研究了HRB600級鋼筋用于邊緣約束構件和墻板時的抗震性能.傅劍平等[4]對配置HRB600級鋼筋的工字形截面剪力墻進行低周反復加載試驗，研究了等強代換前后配置600 MPa級和400 MPa級2種墻體的性能差異，考慮配筋率、軸壓比對抗震性能的影響.本文使用ANSYS有限元軟件對暖磚墻體分別進行擬靜力分析，研究配置高強鋼筋的墻體與配置普通鋼筋的墻體在等強代換原則下抗震性能的差異.對配置高強鋼筋的墻體考慮軸壓比、剪跨比2種因素，對抗震性能進行對比分析.

1 暖磚有限元模型的建立

1.1 模型尺寸及配筋

HSSW1—HSSW3為配置了HRB600級鋼筋的暖磚墻體，CSSW1為配置HRB400級鋼筋的暖磚墻體.HSSW是將CSSW1的端柱縱筋、端柱箍筋以及墻體水平分布筋、墻體豎向分布筋按照“等強代換”原則配置了HRB600級鋼筋.4片墻體的尺寸及配筋如圖1所示.CSSW1，HSSW1，HSSW3三片墻體豎向軸力均為3028 kN，對應軸壓比為0.38；HSSW2豎向軸力為1514 kN，對應軸壓比為0.19.墻體的詳細參數見表1.

表1 墻體參數

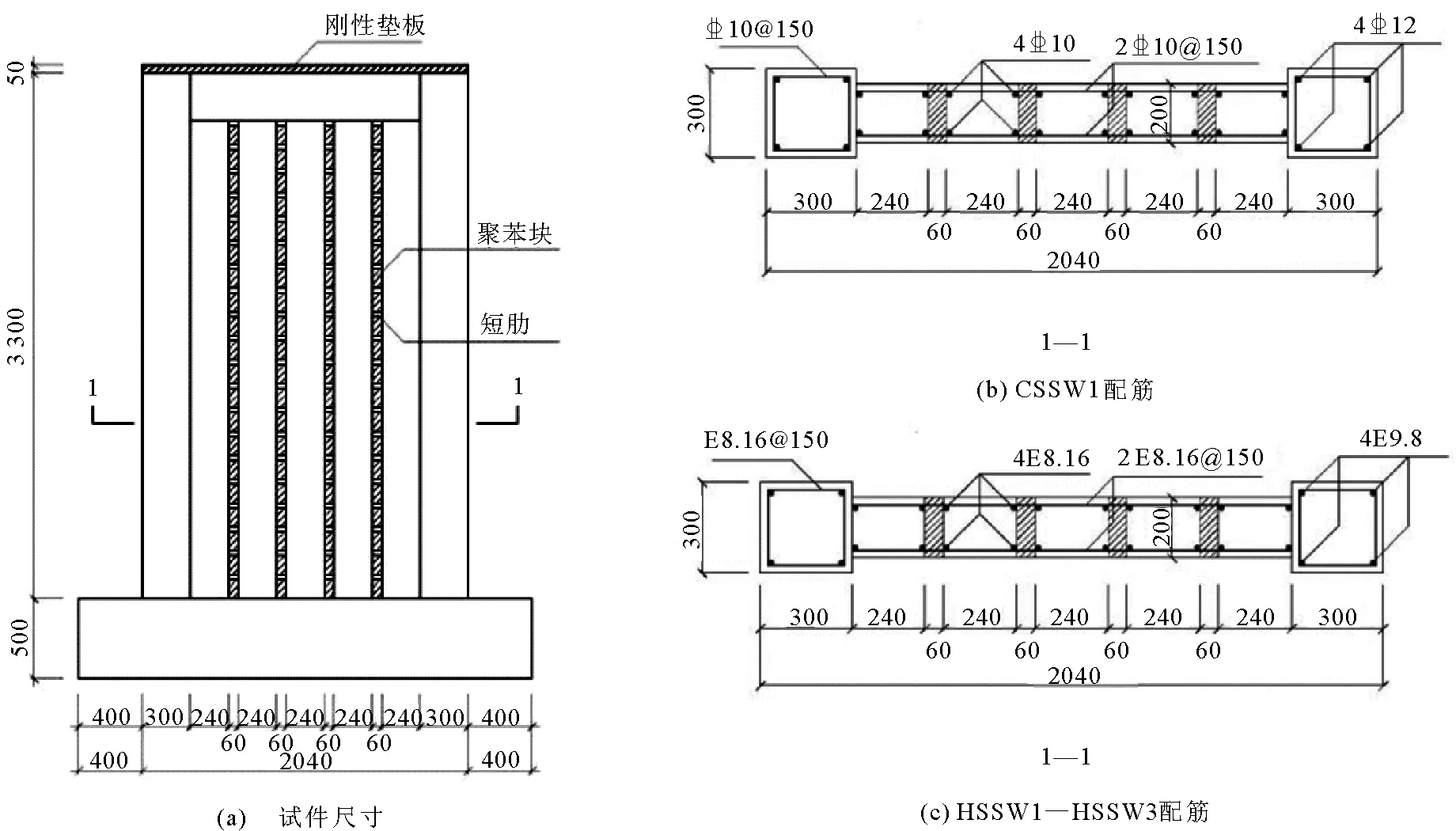
圖1 墻體尺寸及配筋

1.2 建模方式和單元類型

墻體采用分離式建模，即假定鋼筋和混凝土之間沒有相對滑移，分別用實體單元和桿單元模擬混凝土和鋼筋.混凝土采用實體單元Solid65，可以模擬混凝土的拉裂、壓碎、塑性形變和蠕變等非線性材料性質.鋼筋采用桿單元Link8，能承受軸向的拉壓但不能承受彎矩作用.為了不讓加載節點處產生較大的應力集中現象導致混凝土提前破壞造成不收斂，在剪力墻的框架梁頂部增加剛性墊板，使用Solid45單元.

1.3 材料本構關系和材料屬性

混凝土本構關系采用多線性隨動強化模型(MKIN)，該模型可以考慮包辛格效應.多線性隨動強化模型的屈服準則為Mises屈服準則，破壞準則采用 William-Warnke五參數破壞準則.應力-應變全曲線方程選用Hognestad提出的本構關系曲線，上升段采用拋物線，下降段簡化為斜直線.其表達式為

(1)

(2)

混凝土的本構關系曲線如圖2(a)所示，圖中E表示混凝土初始彈性模量，混凝土加載與卸載時的彈性模量都為E；ε0的值為0.002；εcu的值為0.0038；σun，εun分別表示混凝土開始卸載時的應力和應變.混凝土材料參數的確定參考《混凝土結構設計規范》(GB 50010—2010)第5.5.1條規定，結構進行彈塑性分析時，材料的性能指標宜取平均值，并宜通過試驗分析確定.按《混凝土結構設計規范》C.2.1平均值的計算方法：

fcm=fck/(1-1.645δc)

(3)

式中：fck為混凝土軸心抗壓強度標準值；δc為混凝土強度變異系數.

模型所選用的混凝土強度等級為C40，抗壓強度平均值為36.05 MPa，抗拉強度取抗壓強度的1/10，即3.605 MPa.

鋼筋本構關系采用通用多線性隨動強化模型(KINH)，可以比MKIN模型定義更多的應力-應變數據點，采用Mises屈服準則.鋼筋的單調受拉應力-應變曲線選用ESMAEILY-XIAO[5]模型，引入屈服點、強化起點、應力峰值點和極限點，能反映出鋼筋線彈性階段、屈服階段、強化階段和軟化階段，如圖2(b)所示.鋼筋的材料參數參考陳昉健對HRB600級鋼筋單調受拉試驗的試驗數據[6].屈服強度fy為600 MPa，鋼筋的彈性模量E為2×105MPa，強化起點與屈服點應變之比為k1，應力峰值點與屈服點應變之比為k2，極限點與屈服點應變之比為k3，鋼筋峰值強度與屈服強度之比為k4，抗拉屈服強度與抗壓屈服強度之比為k5，鋼筋的材料參數取值見表2.

圖2 混凝土和鋼筋的本構關系

表2 鋼筋的材料參數

1.4 網格劃分

ANSYS判斷混凝土單元是否開裂時使用的是最大拉應力開裂依據，網格質量不佳容易導致應力集中現象，混凝土的抗拉強度較小，容易造成混凝土單元的提前開裂，造成收斂困難，所以為了盡量避免應力集中現象，單元尺寸應控制在50～100 mm，且盡量使用六面體單元[7].為了避免混凝土提前開裂導致不收斂，模型中忽略了保護層厚度.

1.5 邊界條件和加載制度

為了不讓地梁產生位移，限制地梁頂部節點在X軸、Y軸、Z軸3個方向上的位移自由度和3個轉動自由度.墻體頂部設置剛性墊板并于其上施加豎向分布力，不限制墻體頂部轉動自由度.加載方式按照《建筑抗震試驗規程》(JGJ/T 101—2015)中規定的荷載-位移混合加載制度，屈服前每級荷載反復1次，屈服后宜反復3次.墻體屈服前采用荷載控制，先多次試算屈服荷載，依次按照屈服荷載的25%，50%，75%，100%分4次加載，屈服后按屈服位移的50%作為位移增量，每級加載循環3次，直到墻體承載力下降到峰值荷載的85%.

2 試驗驗證

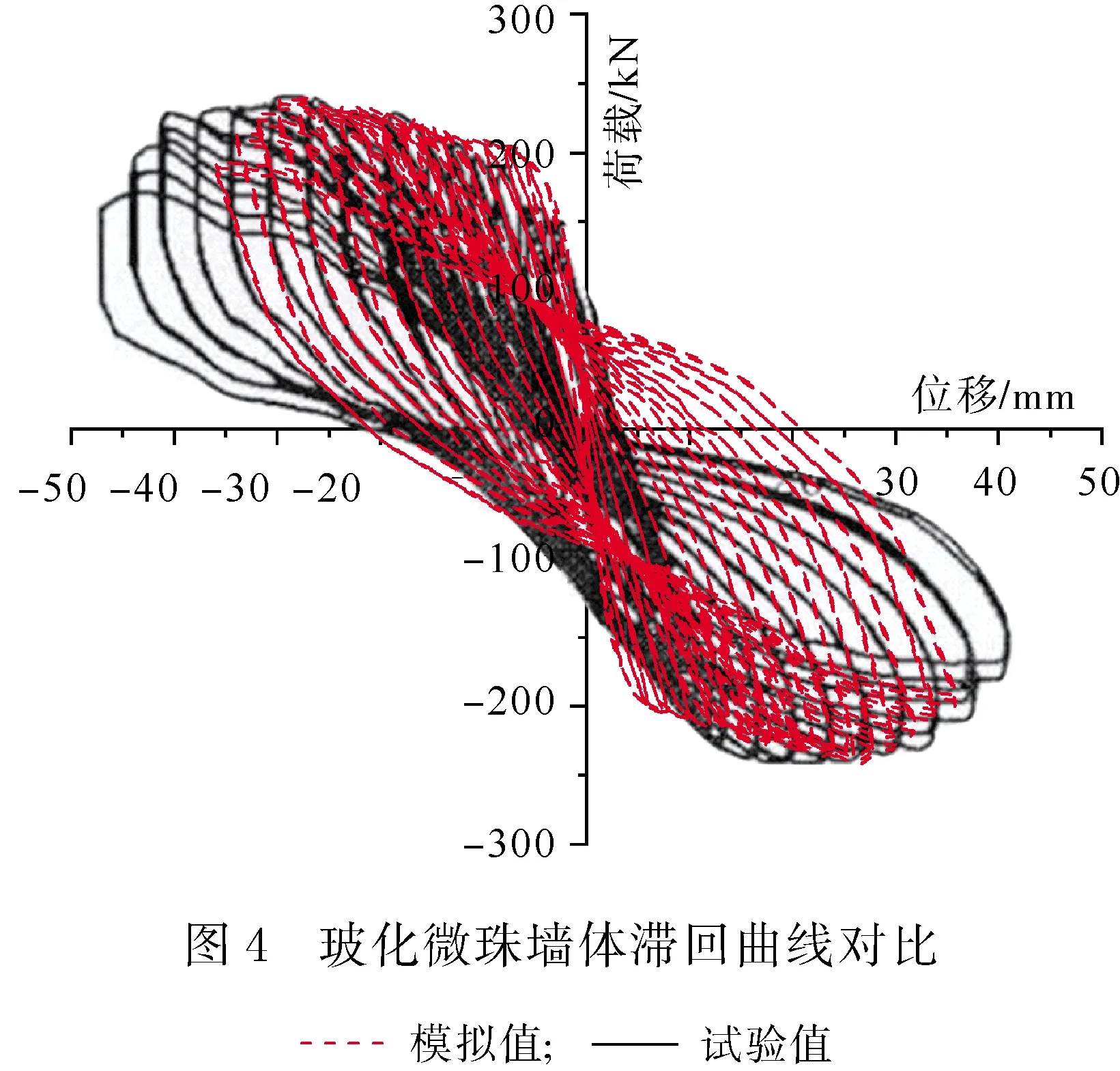
本文選擇朱民偉[8]所做的玻化微珠免拆模復合剪力墻擬靜力試驗為驗證，該類型的墻體與暖磚墻體的區別主要在于保溫墻模的材料和尺寸的不同.對SSW1250墻體進行有限元模擬.混凝土強度等級為C40，本構關系采用Hognestad應力-應變曲線；鋼筋牌號為HPB235，本構關系采用彈性-強化模型.材料屬性均采用文獻中材料性能試驗的結果.有限元模擬的加載制度與試驗所采取的保持一致，屈服前采用荷載控制分級加載，屈服后采用位移加載，每級加載循環往復2次，試驗結果與模擬結果的對比見表3.與試驗值相比，模擬所得的開裂荷載、開裂位移及屈服位移偏小，屈服荷載、峰值荷載及峰值位移符合較好.圖3為墻體破壞時的裂縫開展情況，圖4為試驗滯回曲線與模擬滯回曲線的對比.

表3 試驗與模擬結果對比

圖3 墻體破壞時的裂縫

3 有限元模型模擬結果及分析

3.1 墻體破壞過程

4片墻體的破壞形式接近，以HSSW1為例分析墻體的破壞過程.由于墻體帶豎縫，墻肢之間只有30 mm厚的短肋相連，最終破壞形式類似于帶豎縫剪力墻的破壞形式[9]，墻肢上下根部縱筋屈服，形成了塑性鉸，裂縫分布廣泛，幾乎布滿墻體.墻體開裂前基本處于線彈性狀態，荷載位移曲線基本為直線.隨著水平荷載的增加，墻體上部的短肋首先開裂，由于洞口的存在，短肋處容易發生應力集中.水平荷載繼續增加，框架柱根部受拉一側出現水平裂縫，緊接著墻肢根部受拉側也出現水平裂縫，墻體下部的短肋開始開裂.水平荷載接近屈服荷載的70%左右時，上下部短肋處的裂縫開始向墻體的4個角部擴展，水平荷載達到屈服荷載的75%時，墻肢上下兩端混凝土均開裂，框架柱下部裂縫先貫通，反向加載后框架柱上部裂縫貫通，與框架柱相連的墻肢開裂范圍比其他墻肢大，這是因為邊緣墻肢受到相連框架柱的拉壓作用明顯，中間墻肢相互之間只有短肋約束，約束作用有限.墻體水平荷載逐漸達到屈服荷載時，框架柱受拉一側外側縱筋屈服，墻體上下的裂縫開始向中部發展，框架柱上斜裂縫傾角接近45°.屈服時混凝土的Mises應力云圖和裂縫分別如圖5(a)和(b)所示，鋼筋應力云圖如圖5(c)所示.繼續增加水平荷載，直到墻體破壞時，墻體基本布滿裂縫，框架柱和墻體縱筋屈服范圍擴大，框架柱端部箍筋也已經屈服，破壞時的鋼筋應力云圖如圖5(d)所示.

圖5 加載過程中墻體的應力云圖和裂縫開展情況

3.2 滯回曲線

4片墻體低周往復加載的滯回曲線如圖6所示.加載前期荷載位移曲線基本為直線，卸載后基本沒有殘余變形，滯回環狹長包圍面積小.開裂后荷載位移曲線開始有彎曲段，卸載后有殘余變形.隨著荷載的增加，曲線開始向位移軸傾斜，墻體的剛度逐漸降低，滯回環越來越飽滿，耗能能力繼續增加；達到峰值承載力后，配置HRB600級鋼筋的HSSW1— HSSW3的滯回曲線有明顯的平直段，表明墻體屈服后的強化階段更長，變形能力更強.配置HRB400級鋼筋的CSSW1更早地到達峰值承載力，滯回曲線下降較早.

比較CSSW1和HSSW1的滯回曲線，二者形狀、飽滿程度接近，表明等強代換后，配置HRB600級鋼筋的墻體抗震性能并不低于配置HRB400級鋼筋的墻體；比較HSSW1和HSSW2，二者形狀接近但HSSW1的滯回曲線更飽滿，耗能能力更強，說明在本次模擬的軸壓比條件下，隨著軸壓比的增加，墻體的耗能能力有提高的趨勢；對比HSSW1和HSSW3，隨著剪跨比的降低，構件的承載能力提高，滯回曲線也較為飽滿，耗能能力良好.

圖6 墻體的滯回曲線

3.3 承載能力和變形能力

圖7是比較考慮等強代換、軸壓比和剪跨比3種因素的骨架曲線.墻體的承載力和位移見表4.

由表4可知：HSSW1，CSSW1的峰值承載力相差不大，但HSSW1的峰值位移更大，說明高強鋼筋的材料性能會在變形的后期發揮出來.HSSW1的屈服荷載和屈服位移比CSSW1有所提高，但是延性有所降低，說明配置HRB600級鋼筋可以提高墻體的屈服荷載，由于HRB600級鋼筋的屈服應力和屈服應變比HRB400更高，所以屈服位移也更高，而2片墻體的極限位移十分接近，因此延性有所降低；對比HSSW1和HSSW2，HSSW1的屈服荷載與峰值承載力都高于HSSW2，但延性低于HSSW2，說明隨著軸壓比增加，墻體的屈服荷載與峰值承載力也隨之增加，但墻體的變形能力降低；對比HSSW1和HSSW3，HSSW3的屈服荷載、峰值承載力高于HSSW1，說明隨著剪跨比的增加，承載能力減小.HSSW3的屈服位移、峰值位移、極限位移都比另外3片墻體要低，延性比HSSW1和HSSW2略高，這是因為暖磚墻體上的豎縫改變了墻體的受力特點，豎縫將墻體劃分為若干墻肢，墻肢協同受力，墻體以彎曲破壞為主，變形能力增強.

表4 承載力、位移及延性

3.4 剛度退化曲線

第i級加載的割線剛度用Ki來表示并按下式計算：

(4)

式中：+Fi，-Fi分別表示第i級加載正、反向峰值承載力；+Xi，-Xi分別表示第i級加載正、反向峰值承載力對應的位移值.

圖8給出了不同影響因素下的墻體剛度退化曲線.可以看出：4片墻體的剛度退化速率前期都較快，后期剛度退化速率變慢最終剛度趨于穩定；HRB400級鋼筋等強代換為HRB600級鋼筋后墻體的剛度變化

圖8 墻體剛度退化曲線對比

不大，甚至CSSW1墻體屈服前剛度略高于HSSW1.這是因為兩類鋼筋的彈性模量是相同的，所以從鋼筋尚未屈服的前期來看，CSSW1的配筋率更高因此剛度更大.但是高強鋼筋的優勢會在后期發揮出來，剛度退化速率更慢；相比于HSSW1，HSSW2的剛度退化更快，說明軸壓比小的墻體剛度退化較快；對比HSSW1和HSSW3，HSSW3的初始剛度約為HSSW1的2倍，但HSSW3的剛度退化也最快.可以看出剪跨比對剛度的影響十分顯著，剪跨比小的構件初始剛度大，破壞的過程中退化速率快.

3.5 耗能能力

墻體的耗能能力常采用等效黏滯阻尼系數he來評價，圖9是4片墻體的等效黏滯阻尼系數和位移的關系.從圖中可以看出，加載前期4片墻體處于線彈性階段，等效黏滯阻尼系數基本一致，隨著墻體進入塑性階段等效黏滯阻尼系數逐漸增大，耗能能力隨著變形的增加不斷增強.

配置600 MPa級鋼筋的墻體耗能能力略小于配置400 MPa級鋼筋的墻體，從極限位移時刻的鋼筋的應力來看，C40的混凝土還不足以完全發揮高強鋼筋的材料性能；對比HSSW1和HSSW2可以看出，墻體耗能能力隨著軸壓比的增大而增大；對比HSSW1和HSSW3，因為HSSW3的承載力較大，初期的耗能能力更好，但是剪跨比較大的墻體在后期有更多耗能能力的儲備.

4 結論

1) 4片墻體的破壞形式接近，短肋處最先開裂，破壞時墻肢上下根部形成塑性鉸，裂縫分布廣泛，最終整面墻體都布滿裂縫.

2) 使用HRB600級鋼筋等強替代HRB400級鋼筋后，HSSW1的屈服荷載和屈服位移比CSSW1分別提高了5.3%，29.1%，峰值承載力基本不變，延性降低了23.7%；配置高強鋼筋可以提高屈服荷載，但是延性會降低，耗能能力也有所下降.

3) HSSW1比HSSW2屈服荷載提高了33.8%，峰值承載力提高了19.74%，延性降低了10.6%.隨著軸壓比的增加，墻體的承載能力增加，同時剛度增加、耗能能力增強，但延性降低.

4) HSSW1比HSSW3的屈服荷載、峰值承載力分別降低了27.5%，27.98%.隨著剪跨比的增加，墻體的承載能力、剛度均會降低.加載初期，剪跨比小的墻體耗能能力較強；加載后期，剪跨比大的墻體有較多的耗能能力儲備.