基于關鍵點及光流的平面物體跟蹤算法

季皓宣燁，梁鵬鵬，柴玉梅，王黎明

（鄭州大學信息工程學院，鄭州 450001）

0 概述

平面物體跟蹤算法在增強現實、監控、基于視覺的控制和重建等計算機視覺鄰域有著廣泛的應用。近年來，研究人員對平面物體跟蹤算法的研究取得了較大進展，但現實中的遮擋、模糊、尺度變換等各類復雜場景，會影響跟蹤器的跟蹤性能［1］。因此，需要設計一個魯棒的平面物體跟蹤算法以適應現實中的復雜場景。

平面物體跟蹤算法分為基于關鍵點［2-4］的平面物體跟蹤算法和基于區域［5-7］的平面物體跟蹤方法。基于區域的方法直接使用圖像中像素點的外觀，并通過優化目標物體與輸入圖像之間的相似度度量確定目標物體的位置，這類方法容易受到尺度變換、部分遮擋以及快速移動等擾動因子的干擾［8］。而基于關鍵點的方法可以視作圖像之間檢測到的關鍵點的匹配問題，通過將目標物體描述為一組關鍵點以及帶有關鍵點標識的描述符集合，使得這類方法能夠捕捉到關鍵點及其局部區域外觀的變化，從而能夠充分探索目標物體本身的結構信息，使基于關鍵點的方法能夠使圖像在受到旋轉、光照以及視角變換等擾動因子下具備不變性［9］。此外，由于這類方法在跟蹤過程中僅利用部分關鍵點匹配就能得到良好的跟蹤結果，因此基于關鍵點的平面物體跟蹤算法適合目標物體被部分遮擋的情況。相較于基于區域的方法，基于關鍵點的方法更能夠適應復雜場景下的平面物體跟蹤。

為進一步提高在各類復雜場景下基于關鍵點的平面物體跟蹤算法的魯棒性，本文提出一種基于關鍵點并融合光流的平面物體跟蹤算法。對目標物體與輸入圖像分別檢測關鍵點以及帶有關鍵點標識的描述符，通過最近鄰匹配方法建立目標物體與輸入圖像之間的關鍵點匹配集合，利用光流法計算圖像序列中目標物體關鍵點的光流，計算出目標物體的關鍵點在當前圖像中的位置，得到圖像之間關鍵點的對應關系。通過相應的懲罰系數，由加權平均的策略將已得到的兩組關鍵點對應關系進行融合，得出修正后目標物體與輸入圖像之間的關鍵點匹配集合，通過魯棒的幾何驗證方法估計目標物體相對于輸入圖像的單應性變換，從而得出當前圖像中目標物體的位置，并在POT［10］數據集上進行實驗證明。

1 相關工作

1.1 基于關鍵點的平面物體跟蹤算法

通過局部描述符尋找圖像間的關鍵點對應關系，是基于關鍵點的平面物體跟蹤算法的核心。該方法的目的是設計更健壯的局部描述符，并探尋利用距離度量改善描述符匹配。文獻［4］將關鍵點匹配問題轉換為分類問題，在進行分類器的訓練時，將一個關鍵點的外觀集合當作一個類用以訓練分類器，因此，計算的開銷轉移到訓練階段的方法能夠快速地執行關鍵點的分類。文獻［11］使用樸素貝葉斯分類框架來表達關鍵點識別問題，通過數百個簡單的二進制特征描述關鍵點鄰域圖像斑塊，并使用分類器計算每個關鍵點類別的后驗概率。為了在跟蹤過程中利用空間和時間的一致性，文獻［12］通過一個度量學習驅動方法學習了一個魯棒的基于關鍵點外觀的模型。文獻［13］對SIFT［2］和FERNS［11］進行改進，使它們能夠在移動設備上進行實時跟蹤。為充分探索對象的結構信息，減少各種擾動因素的干擾，文獻［8］提出了基于圖的跟蹤器Gacker，文獻［14］將關鍵點匹配和變換估計結合到一個統一的框架中，并且采用線性結構化支持向量機（SVM）使對象模型快速適應給定的環境。

1.2 光流法

光流法是一種利用光流方程求解目標在圖像平面上運動參數的方法。基于光流的跟蹤方法［15］由于高效的特性而受到廣泛的關注。按照理論基礎與數學方法的區別，文獻［16］將光流計算技術分為基于梯度的方法、基于區域匹配的方法、基于能量的方法和基于相位的方法4 種。基于梯度的方法稱為微分法，利用時變圖像灰度的時空微分計算像素點的速度矢量，具體代表為Horn-Schunck 光流計算方法［17］，該方法通過在光流基本約束方程的基礎上附加全局平滑假設，從而計算出光流場。文獻［18］采用有條件的平滑約束，通過加權矩陣的控制對梯度進行不同的平滑處理。針對多運動的估計問題，文獻［19］提出了分段平滑的方法。基于區域匹配的方法［20-21］通過定位相似區域，由相似區域的位移計算光流，通過對圖像序列進行時空濾波處理，使基于能量的方法［15，22］適于均勻的流場。文獻［23］提出了基于相位的方法，根據與帶通速度調諧濾波器輸出中的等相位輪廓相垂直的瞬時速度來定義分速度，使帶通濾波器按照尺度、速度和定向來分離輸入信號。針對大位移在弱紋理情況下的光流信息計算誤差較大的問題，文獻［24］提出一種基于改進V1-MT 前饋模型的光流計算方法，能在大位移、弱紋理情況下更為準確地計算光流信息。近年來，利用神經網絡建立的光流計算技術［25-26］取得了廣泛的關注與研究。

2 基于關鍵點并融合光流的跟蹤過程

在實現本文算法的過程中，對于基于關鍵點的平面物體跟蹤算法的選取，由于基于SIFT［2］的平面物體跟蹤算法是這類方法中的一個經典的方法，并且在平面物體跟蹤任務中具有良好的表現［10］，因此本文將目標物體的SIFT［2］關鍵點處的光流引入基于SIFT［2］的平面物體跟蹤算法中。

基于關鍵點并融合光流的平面物體跟蹤算法的主要思想是根據相應的懲罰系數，對由SIFT［2］和光流法建立的圖像間的兩組對應關系，通過加權平均的方式進行融合，生成最終的對應關系。這兩個懲罰系數會根據不同算法在同一個有序圖像序列下的表現，增強或削弱其對修正后匹配點位置的貢獻。

2.1 基于SIFT 的關鍵點匹配集合

對輸入的帶有目標物體M的圖像序列I，需要使用SIFT［2］構建I中的圖像與M之間的關鍵點匹配集合。對目標物體M，由高斯差分函數來識別潛在的對于尺度以及旋轉不變的關鍵點。首先通過圖像的尺度變換以及高斯差分生成高斯差分金字塔，尋找極值點確定候選關鍵點。然后通過泰勒展開去除低對比度的特征點，并由海森（Hessian）矩陣消除邊緣的響應點。由上述方法對M構建關鍵點集合K0，以K0中每個關鍵點為中心采樣周圍16×16 作為特征區域，計算區域內每個像素點的梯度幅值與方向，統計個數最多的方向為該關鍵點的主方向，將坐標軸旋轉至主方向，隨后將每個特征區域分為4×4 的子域，每個子域計算8 個方向（45°，90°，…，360°）的梯度方向直方圖，通過繪制每個梯度方向的累加值，形成一個種子點，這樣對16 個子域生成16 個包含8 個方向向量的種子點，這樣就生成了128 維的SIFT 特征向量，經過歸一化后生成關鍵點的描述符集合D0，構建元組(K0，D0)。

為便于說明基于SIFT 的匹配點集合的構建過程，以圖像序列I中的第i張圖像Ii為例。用SIFT 算法提取Ii的關鍵點集合KIi及存儲關鍵點標識的描述符集合DIi，構建元組(KIi，DIi)。對D0中的第m個描述符D0，m以歐式距離作為相似度度量，采用暴力匹配的方式，找出DIi中與D0，m最相似的描述符DIi，n，由關鍵點的標識(m，n)得到匹配的關鍵點對(K0，m，KIi，n)，可以表示M與Ii之間一對匹配的關鍵點。隨后將元素(K0，m，KIi，n)送入關鍵點匹配集合中。重復上述過程直至遍歷K0中所有的元素。至此，對圖像Ii構建出基于SIFT 的關鍵點匹配集合。

2.2 融合光流的關鍵點匹配集合修正

本文使用Lucas-Kanade［27］算法計算目標物體的關鍵點集合K0中每一個關鍵點的光流，該算法基于亮度不變假設和鄰域光流相似假設兩個不變性假設。基于上述兩個假設，對時刻t時的圖像函數Img（x，y，t）建立光流方程，由最小二乘法可得近似解：

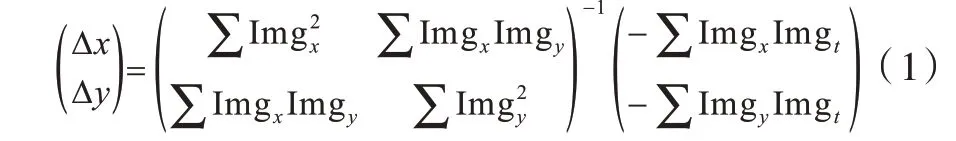
其中，Img 表示整幅圖像，Imgx、Imgy、Imgt分別表示Img 對x、y、t的偏導數，由式（1）得出(Δx，Δy)，表示在時刻t時x、y方向的速度。

對有序圖像序列I，有第一張圖像I0以及預先指定的目標物體的關鍵點集合K0，對光流法F，有LI1=F(K0)，LI2=F(LI1)，…，LIn=F(LIn-1)，其中，LIn為In中與K0對應的點的集合，與K0中的坐標是一一對應的。同理，對圖像Ii，由上述過程得出的點的集合LIi，由LIi與K0構建對應關系：

其中，Ind（x）為指示函數，當x成立時，Ind（x）=1，否則Ind（x）=0，Δ(a，b)表示a、b之間的歐氏距離。

為計算λ1、λ2的值，本文基于以下的觀察：在SIFT進行平面物體跟蹤的過程中，圖像序列中的前N（N較小）張圖像所預測的跟蹤框通常是可靠的。基于該觀察對圖像序列中的前N張圖像，計算這些圖像中目標物體的單應性變換矩陣。由K0中元素的位置，通過透視變換得到變換后的點TruthIi。此時，記CL為僅使用Lucas-Kanade 進行關鍵點對應時發生錯誤（Δ(LIi，m，TruthIi，m)＞μ1r）的次數，CS為僅使用SIFT 進行關鍵點匹配時發生錯誤（Δ(KIi，n，TruthIi，m)＞μ1r）的次數。對(λ1，λ2)的值，由式（4）計算：

通過式（3）、式（4）可以得出修正后的匹配點集合?Ii。由魯棒的矩陣估計方法，對?Ii計算單應性矩陣HIi，由HIi與序列I中第1 張圖像中目標物體M的標注點，通過透視變換得出圖像Ii中目標物體的位置預測值RIi，即為Ii中目標的跟蹤結果。算法1 描述了基于關鍵點并融合光流的平面物體跟蹤算法對輸入圖像序列中目標物體M的跟蹤過程。

算法1基于關鍵點并融合光流的平面物體跟蹤算法

3 實驗

通過實驗在公開數據集上評測了本文提出的算法（SIFT+OF），并與SIFT［2］、FERNS［11］、SURF［3］、SOL［14］、GPF［28］、SCV［6］、ESM［7］、GO-ESM［20］、IC［5］、L1APG［29］和IVT［30］11 個經典算法進行了比較。

3.1 數據集

實驗所用數據集為POT 數據集［10］，該數據集對30 個物體的7 種運動狀態進行采集，這7 種運動狀態分別是尺度變換、旋轉、透視失真、運動狀態的模糊、遮擋、出視野和無限制移動。POT 數據集中每張圖像的像素為1 280×720，有52 500 張圖像標注了目標物體4 個角點的坐標，由于數據集中的圖像序列均為野外場景拍攝，因此可以很好地模擬實際應用中復雜多變的環境。

3.2 評價指標

按照文獻［10］中的評測辦法，以校正誤差作為評價指標，該指標基于物體的4 個角點，計算跟蹤器預測的跟蹤結果與真實值之間的歐氏距離的平均值，如式（5）所示：

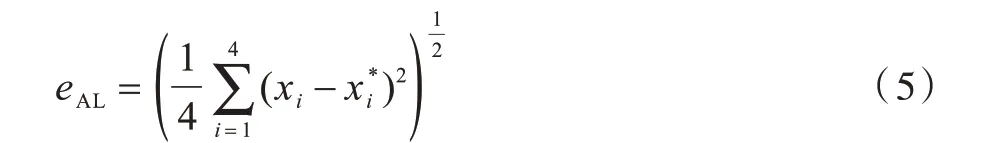
其中，xi是跟蹤器預測的目標物體的4 個角點坐標，為真實標注的目標物體4 個角點的坐標。

通過精度圖反映跟蹤器的質量［31］，它表示校正誤差eAL小于閾值tp的幀所占的百分比。

3.3 實驗結果與分析

本次實驗環境為Ubuntu16.04 系統，使用OpenCV3.2.0 設計實現，實驗設備為CPU：Intel Core i7-7700HQ CPU，內存16 GB。實驗參數設置為閾值μ1=1，μ2=3，半徑r=3，N=10。為驗證SIFT 與光流融合的平面物體跟蹤算法（SIFT+OF）的有效性，本文實驗評測了SIFT+OF 在平面物體跟蹤任務［10］中的跟蹤精度以及跟蹤速度。

3.3.1 平面物體跟蹤任務

本節評估了SIFT+OF 在POT 數據集［10］上的跟蹤精度，并與11個經典的平面物體跟蹤算法［2-3，5-7，11，14，20，28-30］的跟蹤精度進行了比較。其中，除SIFT+OF 外，其余算法的結果均引用文獻［10］中的評測結果。圖1 為12 種算法在7 種運動狀態下的跟蹤精度圖以及所有狀態下的平均結果，其中tp為校正誤差閾值。表1 為校正誤差閾值tp=5 時的跟蹤精度，其中最優值加粗表示。

圖1 不同算法在POT 數據集中的跟蹤精度Fig.1 Tracking accuracy of different algorithms in the POT dataset

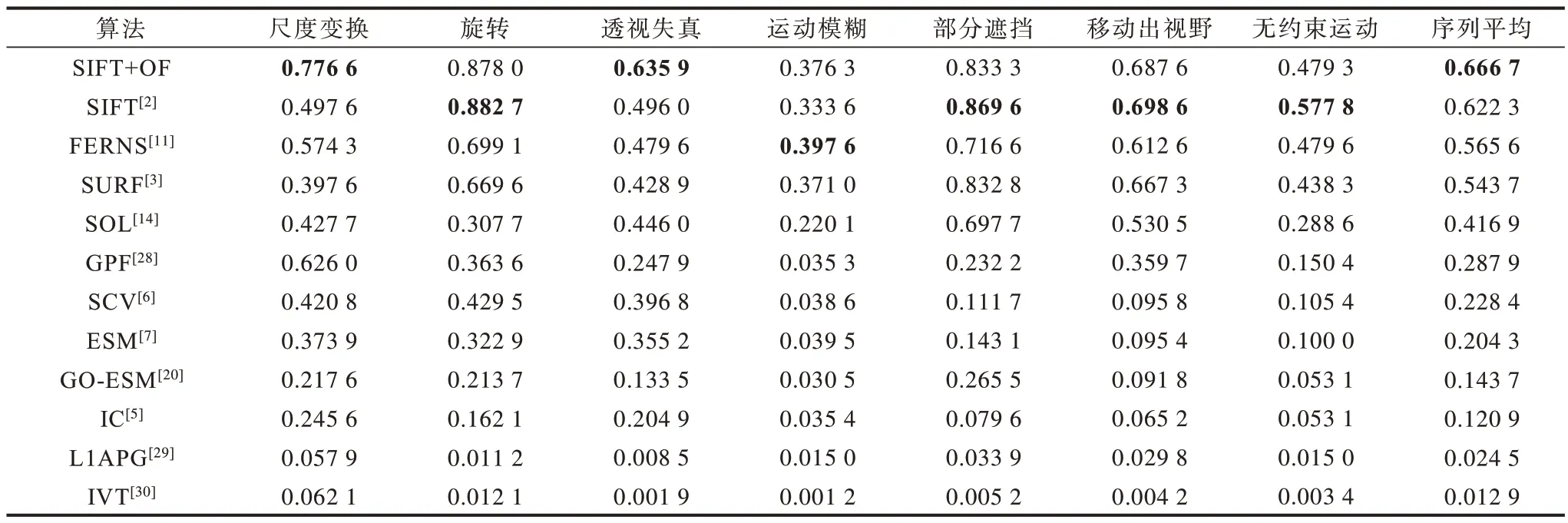
表1 校正誤差閾值為5 時不同算法在POT 數據集中的跟蹤精度Table 1 Tracking accuracy of different algorithms in the POT dataset when the correction error threshold is 5

實驗結果表明，將SIFT 與光流融合的平面物體跟蹤算法（SIFT+OF）優于基于SIFT［2］的平面物體跟蹤算法。特別地，在尺度變換（圖1（a）、表1）、透視失真（圖1（c）、表1）狀態下取得最好的效果，運動模糊（圖1（d）、表1）優于基于SIFT 的平面物體跟蹤算法。從整體表現來看，在校正誤差閾值為5 時，SIFT+OF 在POT 數據集［14］中的跟蹤精度與基于SIFT［2］的平面物體跟蹤算法相比，提高了4.4%。

3.3.2 跟蹤速度對比

由于SIFT+OF 與基于SIFT［2］的平面物體跟蹤算法相比增加了額外計算，為探究SIFT+OF 的運行速度，本文對SIFT+OF 與11 種經典的跟蹤算法的運行速度進行測評。表2 統計了各個算法的跟蹤速度。

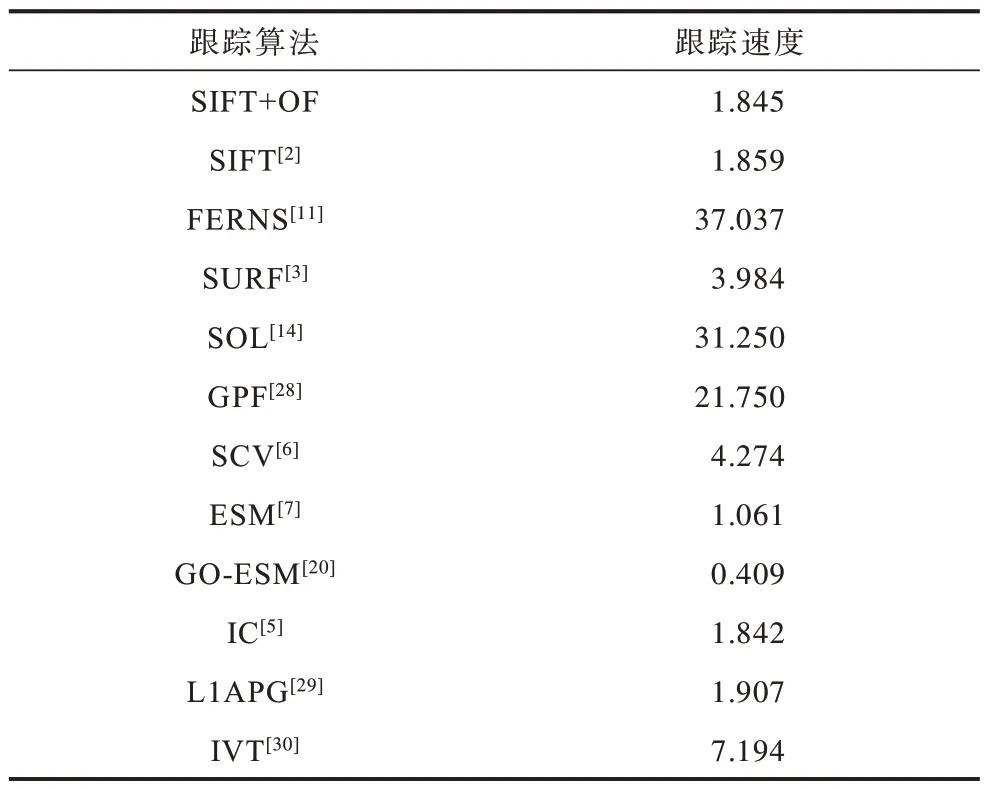
表2 不同算法在POT 數據集中的跟蹤速度Table 2 Tracking speed of different algorithms on the POT dataset（frames·s-1）

從表2 可以看出，對FERNS［11］而言，由于計算的開銷轉移至訓練階段，因此具有更高的運行速度，而SIFT+OF 與SIFT［2］具有相似的運行速度，更具體地，SIFT［2］的跟蹤速度為1.859 frames/s，略快于SIFT+OF 的1.845 frames/s。因此，可得出SIFT+OF 的運行速度稍慢于SIFT［2］算法。綜合上述的實驗結果及分析可以得出，本文提出的算法（SIFT+OF）能夠在平面物體跟蹤的評測任務中取得良好的表現，且具有較高的運行速度。

4 結束語

本文提出一種基于關鍵點并融入光流的平面物體跟蹤算法。將Lucas-Kanade 算法計算的目標物體關鍵點的運動信息融入SIFT 算法特征匹配的過程中，根據加權平均策略對目標物體與輸入圖像關鍵點的對應關系進行調整，從而得出目標與輸入圖像關鍵點之間的對應關系。利用魯棒的幾何驗證方法計算目標物體在當前圖像中的單應性變換，基于該變換矩陣，通過目標物體關鍵點的角點坐標由透視變換得出跟蹤結果。基于POT 數據集52 500 張帶標注圖像的實驗結果表明，該算法相比經典的跟蹤算法能夠取得更高的跟蹤精度。下一步研究是將基于深度學習的方法與本文提出的方法相結合，在保證跟蹤速度的同時，提高對圖像序列中目標物體的跟蹤精度。