基于視覺傳達效果的圖像壓縮感知重建算法研究

沈鳳仙

(三江學院 計算機科學與工程學院， 江蘇 南京 210000)

0 引言

磁共振成像(Magnetic Resonance Imaging，MRI)技術能夠提供活體組織的細節圖像，同時具有對人體無輻射性傷害等優點，因此被廣泛地應用于人腦、胸部、心臟以及人體其他部位結構的成像。但是，MRI成像技術存在成像速度慢的缺點，這樣會導致心臟成像、腹部成像和功能成像中產生偽影；另外，由于過長的采樣時間會造成患者心理的不適感。為了提高MRI數據采樣速度和成像速度，Crawley和Wajer等人采用部分傅里葉變換和非笛卡爾采樣實現k空間數據的欠采，但是會引入部分圖像偽影。壓縮感知(Compressed Sensing，CS)最早由Donoho[1]和Cande[2]等人提出，其打破了傳統采樣理論對采樣頻率的限制，可以采集數據且可以壓縮采集的數據，能夠降低數據采樣量、節約數據的存儲空間以及計算時間。CS最先由Lustig[3]引入MRI圖像的采集和重建，從k空間隨機欠采樣產生的偽影視為噪聲的角度出發，通過最小化l1范數的非線性重建實現MRI圖像中偽影的去除。

為解決MRI圖像欠采樣易產生階梯狀偽影的問題，Knoll等人[4]提出一種基于高階總變分法的圖像重構偽影去除法，實驗結果表明，可以有效地抑制階梯狀偽影。

Qu等人[5]提出一種聯合稀疏變換的MRI圖像重構算法，通過一個稀疏變換重構偽影實現另外一個稀疏變換的抑制，達到MRI圖像偽影的去除，實現圖像重構質量的提高。

Islam等人[6]結合小波域和高斯模型，提出一種基于小波域的高斯混合尺度模型的MRI圖像欠采樣重構算法，實驗結果表明，該方法同傳統方法相比較可以提高信噪比0.5 dB，效果較好。

目前，稀疏變換和表示在MRI圖像重建處理中發揮著重要作用，曲波變換作為圖像稀疏變換的重要方式已被廣泛地應用于圖像處理。但是，傳統的曲波變換只能提取有限的方向性信息，且變換基也是預先設定的，因此無法完全抑制圖像的噪聲和保留圖像的邊緣信息。針對傳統曲波變換存在的缺點，將圖像分塊理論引入壓縮感知圖像重建，結合曲波變換具有適合表達邊緣細節信息和曲線信息的優點，利用曲波變換對MRI圖像進行稀疏表示，提出一種基于圖像分塊的曲波變換的MRI圖像壓縮感知圖像重構算法，從而實現MRI圖像噪聲的抑制和邊緣信息的保留。

1 壓縮感知MRI(Compressed Sensing MRI，CS-MRI)

Do等人[7-10]研究發現二維小波變換缺少稀疏表示光滑邊緣和輪廓的能力，使得重建后的MRI圖像仍然存在偽影現象。針對小波變換無法實現最優逼近，本文結合曲波變換具有適合表達邊緣細節信息和曲線信息[11-12]，采用曲波變換對MRI圖像進行稀疏表示。

MRI圖像稀疏重建實質上是求解l1范數最優化的問題[13-16]，如式(1)。

(1)

式中，l1范數||α||1表示向量α中所有元素的絕對值之和。交替方向優化算法被廣泛地應用于MRI圖像重建，其可以將式(1)的最優化問題轉化[17]，如式(2)。

(2)

式中，ψH表示稀疏變換，主要實現圖像x的稀疏化；傅里葉欠采算子FUx表示被重構的MRI圖像；y∈CM表示獲得的k空間數據。

2 圖像塊的方向性曲波變換的CS-MRI圖像重建

2.1 圖像塊方向性曲波變換(Graph Patch-based Directional Curvelet Transform，GPBDCT)

MRI圖像分塊結果，如圖1所示。

(a) 分塊結果

令φT表示圖像x的二維正向曲波變換，Rj表示將圖像x系數φTx分成塊的算子bj=RjφTx(j=1,2,…,J)，實現圖像的分塊操作，候選方向集為θ={θ1,θ2,…,θd,…,θD}，對于第j個塊的幾何方向，那么曲波變換域內子帶系數塊的幾何方向wj能夠通過S個曲波系數的最小逼近誤差實現估算[18]，如式(3)。

(3)

(4)

(5)

式中，c表示每個像素的重疊系數。

2.2 基于PBDCT的CS-MRI圖像重建

在CS-MRI圖像重建過程中，通過約束變換系數的l1范數，使得其最小化，而l0范數則能用較少的測量值實現圖像重建。因此，通過約束l0范數最小化進行MRI圖像重建，其重建式，如式(6)。

(6)

2.3 算法流程

為了方便求解和計算，將輔助變量αj=ψTP(θj,d)Rjx引入式(6)，則有式(7)。

(7)

式(7)在求解過程中，隨著β的增大，前一次β值的解作為下一次β下的初始解。當β值一定時，式(7)通過下面兩步實現求解。

(1) 固定x，計算每一個αj，如式(8)。

(8)

(9)

式(9)可以通過正則化方程進行求解，如式(10)。

(10)

由于ψψT=I,PT(θj)P(θj)=I，式(10)可以簡化，如式(11)。

(11)

MRI圖像系數重建結果，如式(12)。

(12)

其算法流程如下。

3 實驗與結果分析

3.1 評價指標

(13)

(14)

(15)

實驗中，采用笛卡爾采樣模板實現k空間數據欠采，如圖2所示。

(a) 35%數據欠采

所有k空間數據均由SIMENS 3T成像儀采集得到，成像參數TR/TE=6 100/99 ms，層厚為3 mm，視野為220*220 mm。

標準實驗圖像，如圖3所示。

(a)

(e)

為評估本文算法的有效性，以圖3(a)-圖3(h)為研究對象，其中，圖3(a)-圖3(d)為笛卡爾坐標采樣圖像，因為笛卡爾坐標采樣被廣泛地應用于工程實踐和科學研究，具有很好的效果；圖3(e)-圖3(h)為2維欠采樣圖像。

GPBDCT、塊方向性曲波變換(Patch-based Directional Curvelet Transform，PBDCT)和平移不變離散余弦變換(Shift-invariant Discrete Cosine Transform，SIDCT)重構結果，如圖4所示。

(e) 模板

圖4表示不同方法MRI圖像重構結果對比圖，圖4(b)和圖4(f)分別表示SIDCT結合l0范數的MRI圖像重構結果和重構誤差；圖4(c)和圖4(g)分別表示PBDCT結合l0范數的MRI圖像重構結果和重構誤差；圖4(d)和圖4(h)分別表示GPBDCT結合l0范數的MRI圖像重構結果和重構誤差。通過對比分析發現，GPBDCT結合l0范數的MRI圖像重構結果優于SIDCT和PBDCT。由圖4(f)—圖4(h)MRI圖像重構誤差可知，提出的GPBDCT比SIDCT和PBDCT在抑制噪聲和保持邊緣細節方面更具優勢。另外，由不同重構方法的評價指標對比結果，如表1所示。

表1 不同重構方法的評價指標對比結果

由表1可知，GPBDCT結合l0范數進行圖像重構，在信噪比(SNR)、相對l2誤差(RLNE)和匹配度(γ)三個評價指標上，均優于SIDCT和PBDCT，GPBDCT結合l0范數的信噪比比SIDCT和PBDCT分別提高了2.8 dB和1.69 dB，相對l2誤差比SIDCT和PBDCT分別提高降低0.015和0.001 9，從而證明本文方法GPBDCT結合l0范數進行圖像重構質量在抑制噪聲和保留邊緣的優越性。

3.2 不同數據采樣頻率對圖像重構質量的影響

為了研究不同采樣頻率，對MRI圖像重構質量的影響，通過對比不同采樣頻率下，GPBDCT、PBDCT和SIDCT三種方法的MRI圖像的相對l2誤差(RLNE)。其對比結果，如圖5所示。

(a)

(c)

(e)

(g)

圖5表示不同方法下，不同采樣頻率對圖像重構質量的影響，其評價指標為相對l2誤差(RLNE)。圖5中的橫坐標表示采樣頻率，采樣頻率分別為0.15、0.25、0.35、0.45、0.55、0.65、0.75、0.85和0.95，縱坐標為相對l2誤差。以圖5(a)為例，SIDCT和PBDCT的相對l2誤差明顯大于GPBDCT，在采樣頻率為0.15時，局部的相對l2誤差高達0.101，隨著采樣頻率的增加，相對l2誤差也隨之降低，GPBDCT法的相對l2誤差總體低于SIDCT和PBDCT的相對l2誤差。圖5中的(a)—(h)分別對應圖3中的(a)—(h)。圖5(b)—(h)表示不同測試圖像的相對l2誤差，通過圖5(b)—(h)可知，GPBDCT方法在不同采樣頻率下，其圖像重構結果均優于SIDCT和PBDCT，從而說明本文算法具有很強的穩定性和魯棒性。

3.3 抗噪能力分析

為了驗證本文算法抵抗噪聲的能力，分別對MRI圖像的k空間的實部和虛部加入方差為0.03的高斯白噪聲。不同方法噪聲圖像重構結果，如圖6所示。

(a) 全采樣加噪圖像

不同重構方法的評價指標對比結果，如表2所示。

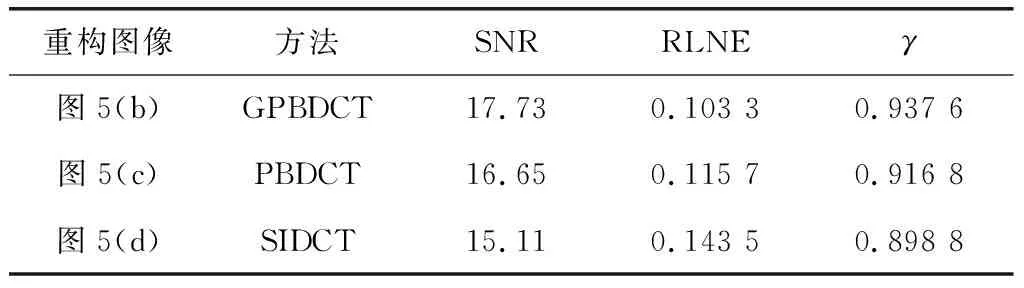
表2 不同重構方法的評價指標對比結果

由表2可知，在信噪比(SNR)、相對l2誤差(RLNE)和匹配度(γ)三個評價指標上，有噪聲MRI圖像重構的信噪比，GPBDCT比SIDCT和PBDCT分別提高2.62 dB和1.08 dB，相對l2誤差分別降低0.040 2和0.012 4，匹配度分別提高0.020 8和0.040 8，從而證明本文算法GPBDCT具有很強的抗噪能力，效果較好，同時在抑制噪聲和保持邊緣細節方面更具優勢。

4 總結

為提高MRI圖像壓縮重構后的視覺傳達效果和圖像重建質量，將圖像分塊理論引入壓縮感知圖像重建，結合曲波變換具有保持圖像邊緣細節信息和曲線信息的優點，利用曲波變換實現MRI圖像的稀疏表示，提出一種基于圖像分塊的曲波變換的MRI圖像壓縮感知圖像重構算法。GPBDCT在進行MRI圖像重構時，從信噪比、相對l2誤差和匹配度三個評價可以看出，本文提出的GPBDCT方法均優于SIDCT和PBDCT，具有很強的抵抗噪聲的能力，在保持圖像細節和邊緣方面效果很好。