剛性包帶式星箭連接裝置解鎖分離過程動力學分析
郭 欣, 朱仕堯, 劉觀日, 于 兵, 唐 科, 雷勇軍
(1.國防科技大學 軍事職業教育技術服務中心,長沙 410073;2.國防科技大學 空天科學學院,長沙 410073;3.北京宇航系統工程研究所,北京 100076)
隨著運載火箭向重型化發展,傳統點式和柔性包帶式的星箭連接裝置已無法滿足其承載要求。新型剛性包帶形式的連接裝置,如圖1所示。(以下簡稱剛性包帶裝置)采用環繞上、下端框的整根楔形截面圓弧包帶作為連接裝置,能夠有效提升星箭連接剛度,具有重要的工程應用價值。
國內外研究人員針對柔性包帶軸向承載能力和分離過程的動力學運動規律已開展了較為深入的研究。秦朝燁等[1-4]對柔性包帶連接的剛度、軸向振動響應和動力學特性進行了分析。白邵竣等[5]基于接觸理論提出了柔性包帶連接的非線性動力學有限元建模方法。譚雪峰等[6-8]提出了包帶分離面徑向沖擊預示的簡化圓環方法,并對包帶連接結構進行了動力學模擬及故障分析。Singaravelu等[9]應用斷裂力學研究了包帶式星箭系統的承載能力。Barrans等[10]采用有限元法對包帶的極限軸向承載能力進行預測。武新峰等[11-12]對包帶連接結構進行優化設計并基于LS-DYNA對分離過程和沖擊響應進行了分析。康士朋等[13]采用解析法和Abaqus軟件研究了溫度變化對柔性包帶裝置預緊力的影響。由于剛性包帶裝置的設計概念提出較晚[14],結構形式、預緊力加載方式以及分離和捕獲方法與柔性包帶差異較大,且涉及熱力耦合、非線性接觸等復雜力學問題,因此目前尚沒有針對剛性包帶裝置的分離運動規律和捕獲回收過程的詳細研究。

圖1 連接狀態下的剛性包帶式星箭連接裝置三維示意圖
針對剛性包帶分離與捕獲過程中的動態響應問題,本文首先介紹了剛性包帶式運載火箭星箭連接裝置的系統組合和結構特點;然后在合理假設基礎上建立其非線性多體動力學有限元分析模型,與試驗結果對比驗證模型正確性;隨后分析剛性包帶接頭速度、解鎖運動軌跡、捕獲運動狀態以及解鎖沖擊等動力學響應特點;最后研究了緩釋解鎖裝置解鎖時間和包帶預緊力等參數對剛性包帶分離與捕獲動力學過程的影響規律。
1 剛性包帶式星箭連接裝置簡介
由圖2可知,剛性包帶形式的運載火箭星箭連接裝置由單條整體式剛性包帶、上下端框、緩釋解鎖裝置以及捕獲器組成。剛性包帶為采用鋁制鍛環制造的整體式包帶,包帶內側為V型槽結構,相比柔性包帶具有較高的結構剛度和強度。剛性包帶兩端接頭均設置有安裝孔,緩釋解鎖裝置固定在安裝孔之間。剛性包帶的頂端和底端分別設有上、下端框,且上端框(即衛星連接端)的底端面和下端框(即火箭連接端)的頂端面均有楔形凸緣,從而與剛性包帶內側V型槽進行連接配合。下端框外壁周向均布安裝捕獲器,且捕獲器的內側安裝有彈簧片,用于實現對剛性包帶的捕獲和限位。
初始狀態的剛性包帶徑向尺寸大于端框楔形凸緣,并呈現開口狀態。在安裝過程中,剛性包帶首先升溫,然后逐漸收緊包帶接頭,使包帶V型槽與上下端框凸緣配合,并用緩釋解鎖裝置固定包帶接頭相對位移,利用包帶自然降溫收縮在內部產生預緊力,實現星箭間連接承載功能。剛性包帶分離時,通過緩釋解鎖裝置緩釋包帶接頭,在儲備的彈性勢能作用下向外彈出,受到捕獲器限制而停止外擴,并在倒鉤型彈簧片作用下減少反彈,最終實現包帶捕獲;與此同時上端框在分離彈簧作用下與下端框實現分離,如圖 2所示。
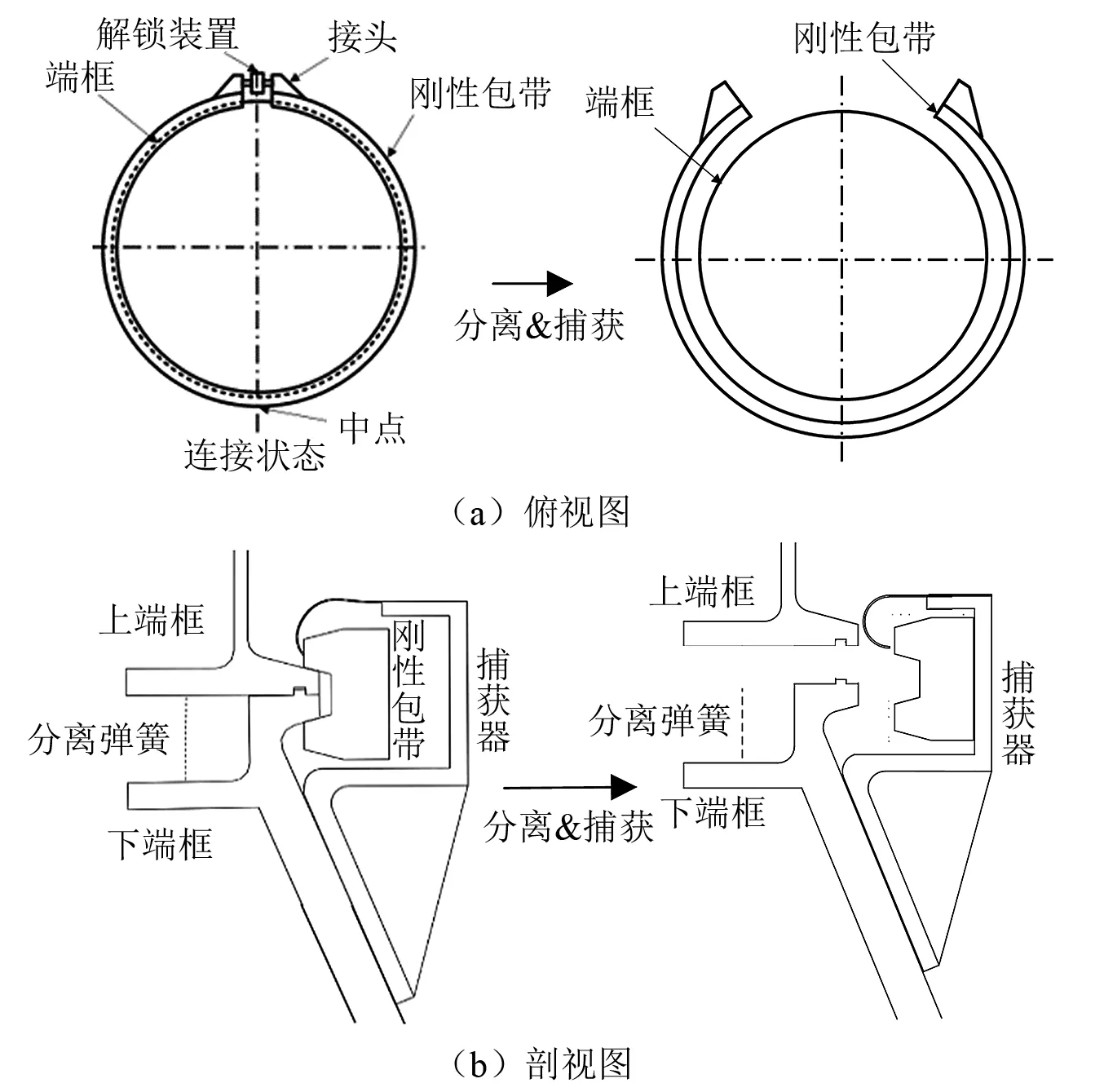
圖2 剛性包帶式星箭連接裝置的分離前后示意圖
2 剛性包帶式星箭連接裝置模型建立
由于剛性包帶安裝和預緊所儲備的彈性勢能在釋放時轉化為分離的動能,該彈性勢能對分離和捕獲過程影響較大,因此本文考慮剛性包帶從自由、連接再到釋放的全過程,將整個仿真過程分為安裝、固定和釋放3個過程。其中安裝過程主要完成包帶升溫和安裝,固定過程主要用來通過降溫產生預緊力,釋放過程主要完成包帶的分離與捕獲。
2.1 連接裝置結構有限元模型
首先,按照圖3所給截面參數繪制上、下端框和包帶的回轉體幾何模型,采用有限元分析軟件Abaqus進行部件網格劃分,除了分離彈簧外所有部件均采用體單元建模,并在有接觸關系的表面劃分較為細致的網格以避免模型接觸失效。然后,根據部件間物理連接關系進行結構系統組集,建立了剛性包帶式星箭連接裝置自由狀態下的有限元模型,如圖4所示。其中共劃分單元59 875個,節點83 910個。上、下端框、包帶以及捕獲器主體結構均為鋁合金材料(牌號2A14T6),僅捕獲器掛鉤部分為不銹鋼材料(牌號PH13-8Mo),相關材料參數如表1所示。
2.2 載荷邊界條件
如表2所示,對不同分析步中載荷與邊界條件進行逐一設置,其中下端框底端固支約束在3個分析步中保持不變;上端框頂端簡支只在安裝過程中施加,以抵消包帶未安裝時的分離彈簧作用力,在包帶安裝后隨即失效。在安裝過程內,先對包帶施加溫度載荷,然后在包帶的接頭處施加位移載荷,使包帶接頭收緊至固定位置。此外,安裝過程只考慮上下端框間、包帶與上下端框和包帶與捕獲器的掛鉤間的接觸,不考慮包帶與捕獲器的接觸,因此包帶可以直接穿越捕獲器進行安裝;而在固定與釋放時間步中考慮所有可能的接觸關系,從而實現捕獲器對包帶的捕獲。
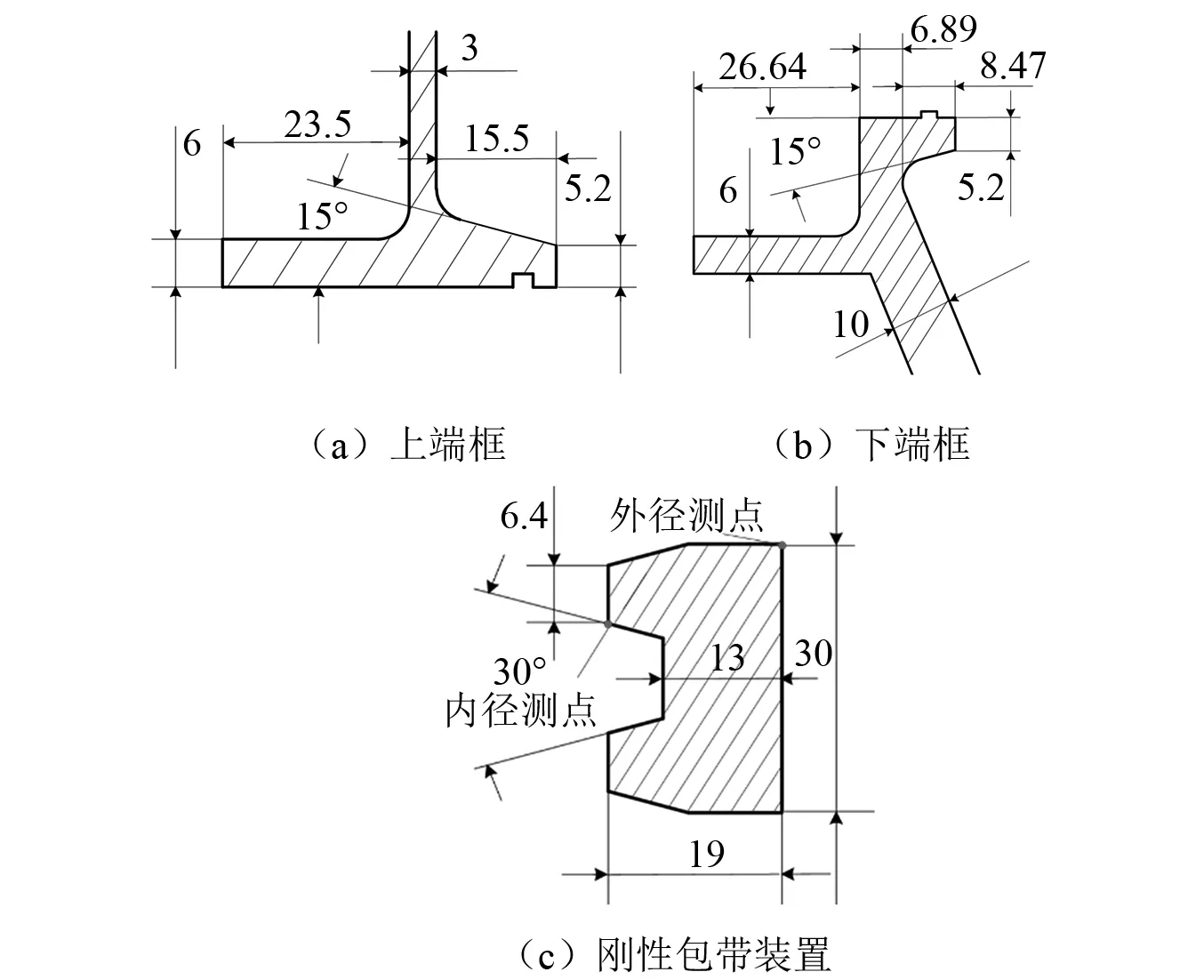
圖3 剛性包帶式星箭連接裝置結構參數(mm)
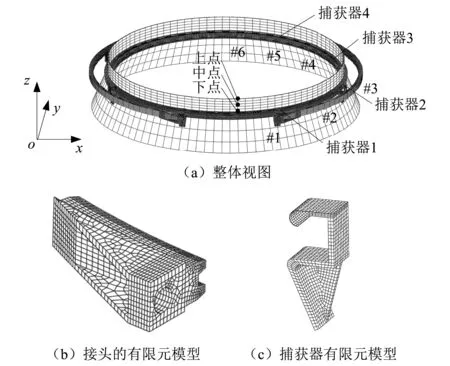
圖4 剛性包帶式星箭連接裝置的有限元模型
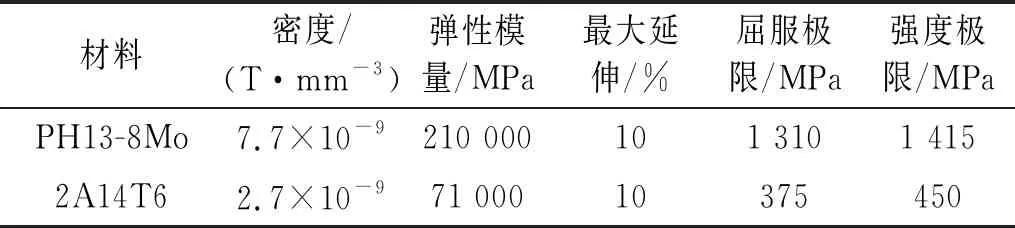
表1 端框和包帶的材料參數

表2 不同分析步中的載荷和邊界變化
2.3 模型正確性驗證
包帶接頭預緊力在安裝-預緊過程中的變化,如圖5所示。安裝過程中,接頭預緊力用于克服包帶自身變形,隨時間緩慢增大;安裝后,包帶熱量向端框傳導,自身溫度逐漸降低,接頭預緊力迅速增大;當兩者溫度趨同時,預緊力趨于穩定。分析結果與地面試驗結果基本吻合,最終預緊力分別為17.9 kN和16.4 kN。剛性包帶在降溫預緊后周向預緊力的分布圖,如圖6所示。從圖6可知,剛性包帶的預緊力從0°(包帶接頭)到180°(包帶中點)逐漸增大。分析結果與試驗結果規律相符。綜上,接頭預緊力變化規律和包帶周向預緊力分布的分析結果與地面試驗結果較為一致,說明所建模型和分析方法合理可信。

圖5 剛性包帶接頭預緊力隨時間變化曲線
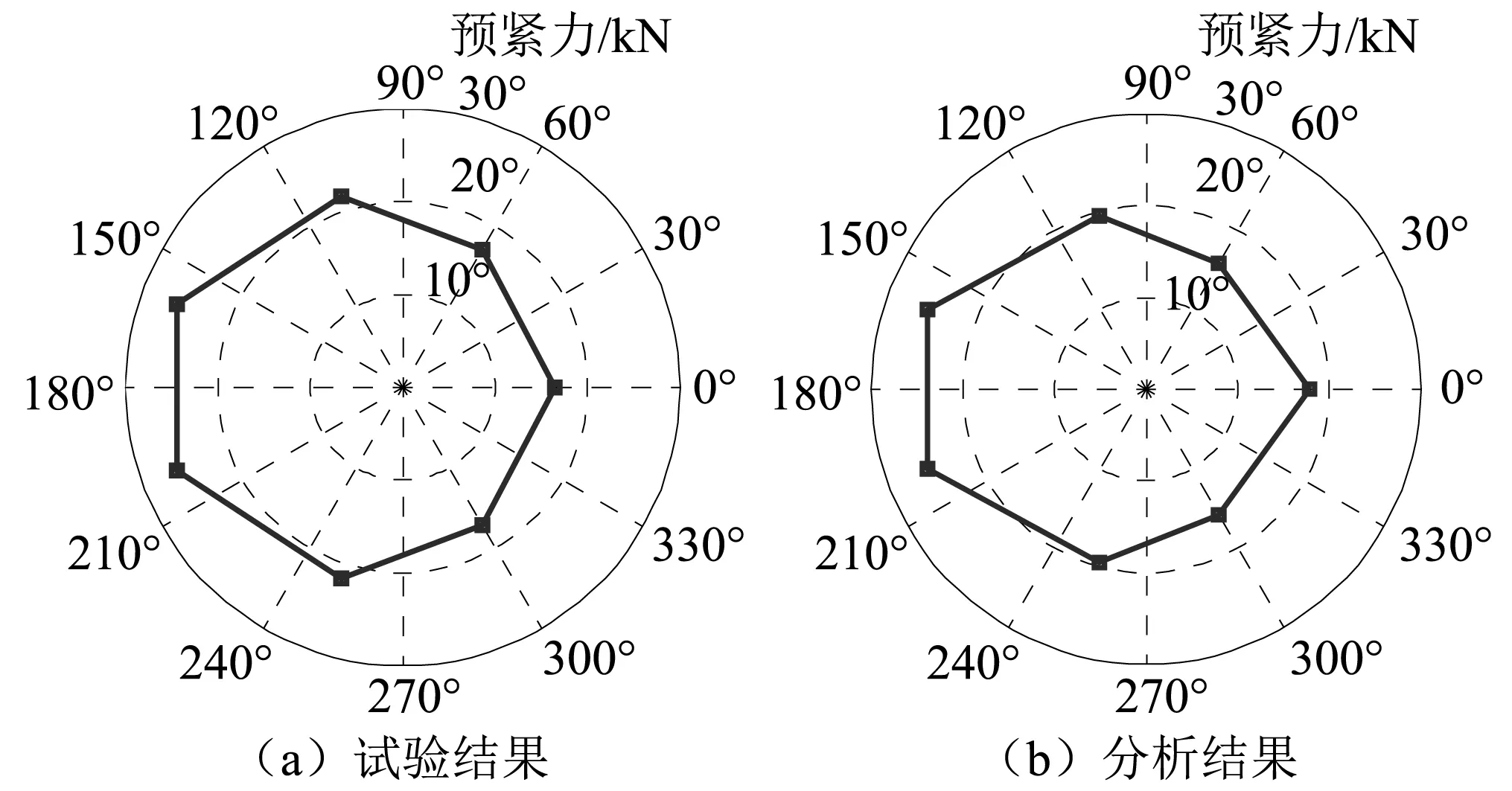
圖6 剛性包帶周向預緊力分布圖
包帶接頭預緊力隨包帶和端框單元總數變化的曲線,如圖7所示。通過對比不同網格細分下的分析結果可以發現:隨著有限元模型網格的不斷細化,單元數量逐漸增大;當單元數量大于59 000時,分析結果對網格尺寸不敏感(相對偏差小于2%);本研究所建模型單元數量達到59 875個,滿足網格無關性要求。
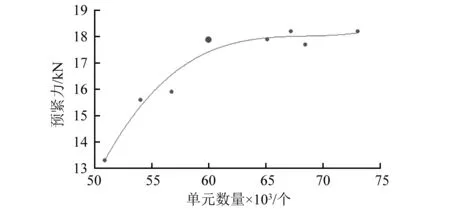
圖7 剛性包帶接頭預緊力隨單元數變化曲線
3 分離與捕獲過程動力學分析
本部分在34 kN預緊力和2 ms緩釋解鎖狀態下,分析剛性包帶分離與捕獲過程中的接頭運動速度、包帶運動規律和上端框沖擊響應。為便于結果討論,在+x側包帶上沿周向選取6個特征截面,其中1#截面為包帶接頭,2#~5#截面依次對應與捕獲器1~4接觸位置,6#截面位于包帶中點,截面位置見圖4(a),測點位置見圖3(c)。取1#截面上的特征點作為接頭速度測點。在與包帶接頭對應的上端框位置,沿+z方向由上至下選取上、中和下3個位置作為沖擊響應測點,測點位置見圖4(a)。
3.1 接頭運動速度分析
①0~2 ms:在該階段包帶處于緩釋狀態,隨著限位載荷逐漸減小,接頭速度隨時間單調遞增至5.72 m/s;此過程整個包帶未與捕獲器碰撞,始終處于外擴狀態;②2~7.2 ms:包帶接頭速度呈現小幅波動式緩慢增長,最大值可達10.01 m/s;此過程中包帶存在釋放殘余振動且各典型截面先后開始碰撞捕獲器,導致接頭速度波動;③7.2~20 ms:接頭速度迅速衰減,隨后在4.00 m/s附近振蕩變化,此過程包帶受到捕獲器阻攔發生反彈,內能與動能開始相互轉化,因此速度具有明顯振蕩特征。
3.2 包帶運動規律分析
包帶內側徑向位置隨時間變化曲線,如圖8(a)所示。其中1#截面在3 ms最先脫離端框,隨后6#和5#截面在3.4 ms附近脫離,2#和4#截面在4 ms附近脫離,最后3#截面在5.9 ms與端框脫離。整個包帶脫離過程持續5.9 ms,其中包帶接頭與中點位置首先脫離,中間部分隨后脫離,最后分離的位置位于2#與3#截面之間(即捕獲器1與捕獲器2之間)。這是由于包帶接頭位置在解鎖過程中最先釋放,而從接頭到中點的包帶預緊力逐漸越大,因此存儲的彈性勢能也越來越多,因此1#和6#截面會較快分離。此外,3#截面位置在18.5 ms后徑向位置又小于端框半徑,但上端框在11.2 ms(圖中豎直線)已高于捕獲器,上下端框完成分離,因此包帶與上端框并不會發生碰撞。
包帶外側徑向位置隨時間變化曲線,如圖8(b)所示。其中1#和6#截面分別在5 ms和7 ms附近沖出捕獲器徑向包絡,隨后包帶5#和2#截面在6.5 ms附近與捕獲器內壁發生碰撞,4#截面與捕獲器碰撞時間為8 ms,而3#截面與捕獲器最后碰撞,碰撞時間為10 ms;以上4個位置與捕獲器碰撞后,2#~5#截面位置均存在小幅反彈。說明捕獲器彈簧片在一定程度上限制了包帶的回彈運動。
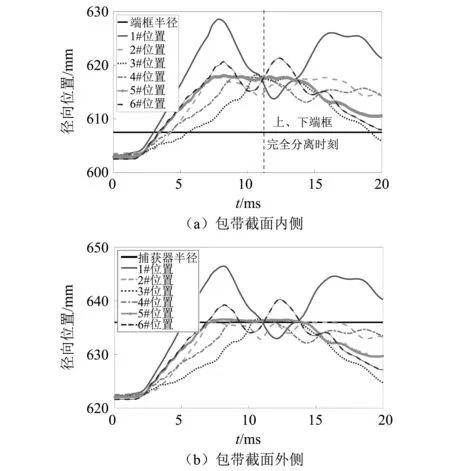
圖8 剛性包帶徑向關鍵位置的徑向位置時間歷程曲線
3.3 上端框沖擊響應分析
上端框測點的沖擊響應時間歷程曲線,如圖9所示。從圖9可知,下點的響應整體幅值最大(峰值為1.9×104m/s2,對應11 ms),中點次之,上點處的響應整體幅值最小(峰值為5.1×103m/s2,對應11 ms)。不難發現:隨著節點位置遠離端框分離截面,分離沖擊響應迅速減小至3.7%,說明分離沖擊對衛星連接端的影響較小。
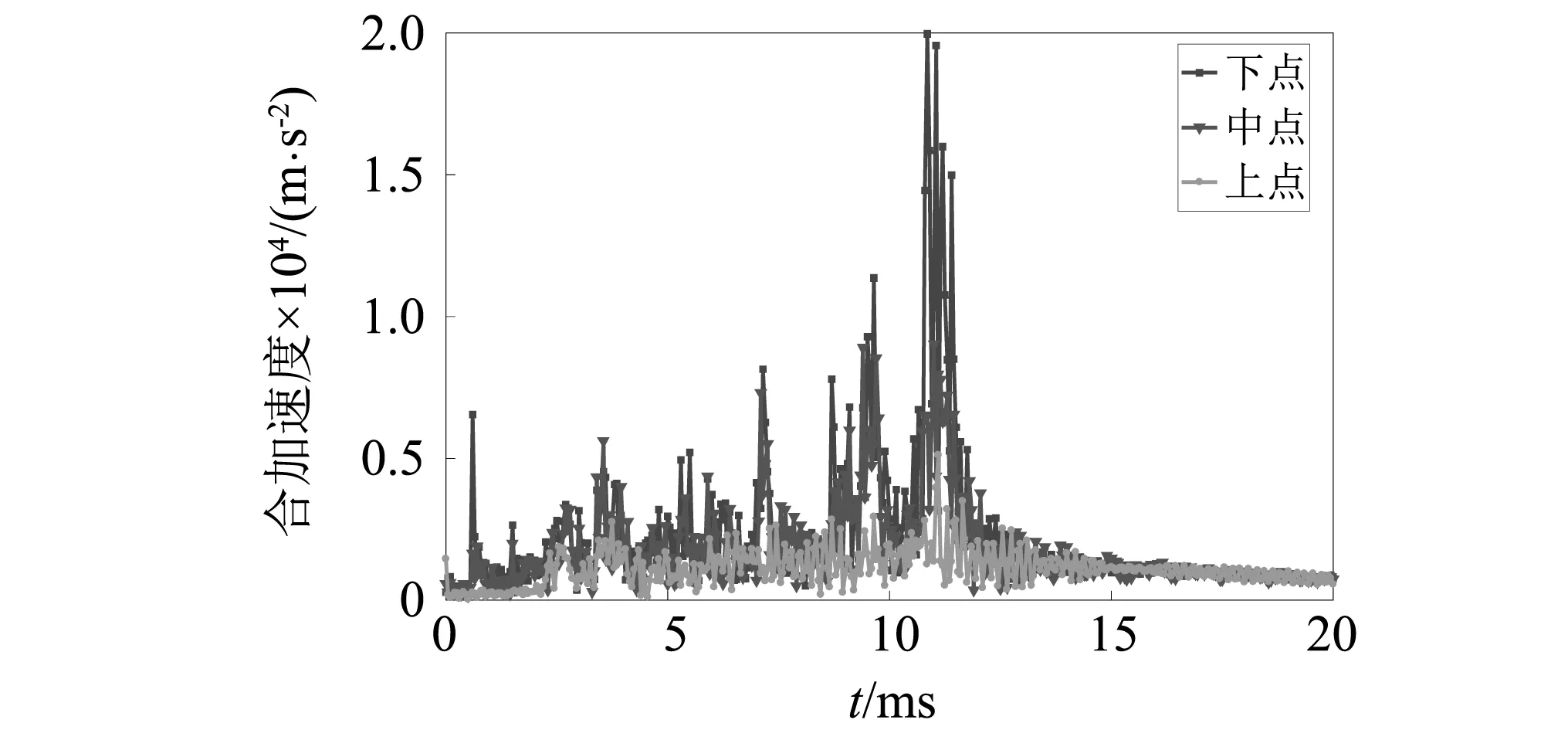
圖9 上端框關鍵測點的加速度沖擊響應
4 包帶分離與捕獲過程影響因素分析
在構型確定的情況下,緩釋解鎖裝置的解鎖時間和剛性包帶的預緊力水平會直接影響剛性包帶分離過程的動力學行為,需要對其影響規律進行詳細研究。
4.1 解鎖時間對包帶運動分離與捕獲過程的影響
當釋放開關啟動后,緩釋解鎖裝置內部螺桿與飛輪需要一定解鎖時間以完成相對螺旋式滑動從而實現解鎖操作,因此解鎖時間(或解鎖速度)會影響預緊剛性包帶的彈性勢能釋放過程,進而影響其分離運動。本部分主要關注包帶解鎖時間對包帶分離和捕獲運動的影響規律,并假設解鎖過程中包帶預緊力按線性規律減小。不同解鎖時間條件下的接頭運動速度時間歷程,如圖10所示。從圖10可知,隨著解鎖時間由2 ms延長至6 ms,接頭速度的變化趨勢較為相似,即緩釋段速度明顯增大,隨后速度增大至峰值并迅速減小,最后呈現波動變化規律。在緩釋過程中的接頭速度整體呈減小趨勢,且速度峰值出現時間逐漸后移,峰值取值由10.01 m/s下降至7.05 m/s,減小29.6%。
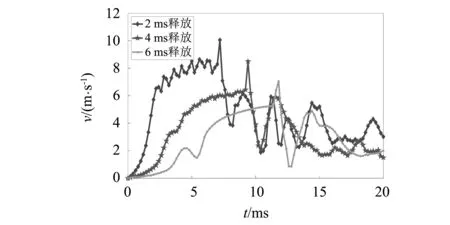
圖10 不同緩釋時間條件下的包帶接頭速度時間歷程
不同解鎖時間條件下的包帶與端框和捕獲器配合時間,如圖11所示。從圖11可知,隨著解鎖時間延長,包帶與端框分離時刻和與各捕獲器接觸時刻均延后。當解鎖時間達到6 ms時,在20 ms內包帶甚至仍未與端框分離,只有接頭位置與捕獲器發生碰撞,并且分離順序由先1#和6#截面再中間截面的順序變為1#~6#截面依次分離。這是由于隨著解鎖時間逐漸延長,包帶分離運動明顯放緩,導致包帶中點處較大的彈性勢能得到緩慢釋放,使#6截面的彈出速度明顯減小,最終包帶呈現從接頭處緩慢展開的運動趨勢。雖然包帶緩慢分離可以降低沖擊響應,但是上述運動趨勢容易導致上端框傾斜分離,在工程實踐中應盡量避免。
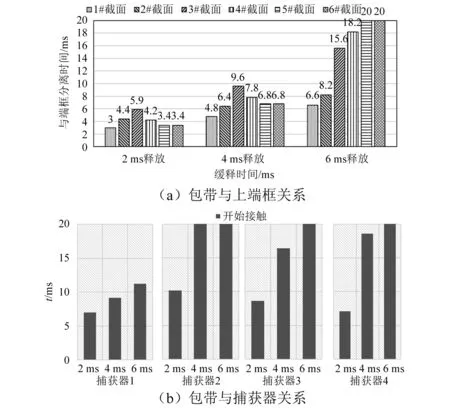
圖11 不同緩釋時間條件下的包帶與端框和捕獲器配合關系
衛星安裝平面處的加速度沖擊響應時間歷程曲線,如圖12所示。從圖12可知,隨著解鎖時間延長,衛星所承受的沖擊響應不斷減小,沖擊峰值出現時間在8~10 ms,峰值取值由1.90×104m/s2下降至1.45×104m/s2,減小23.7%。
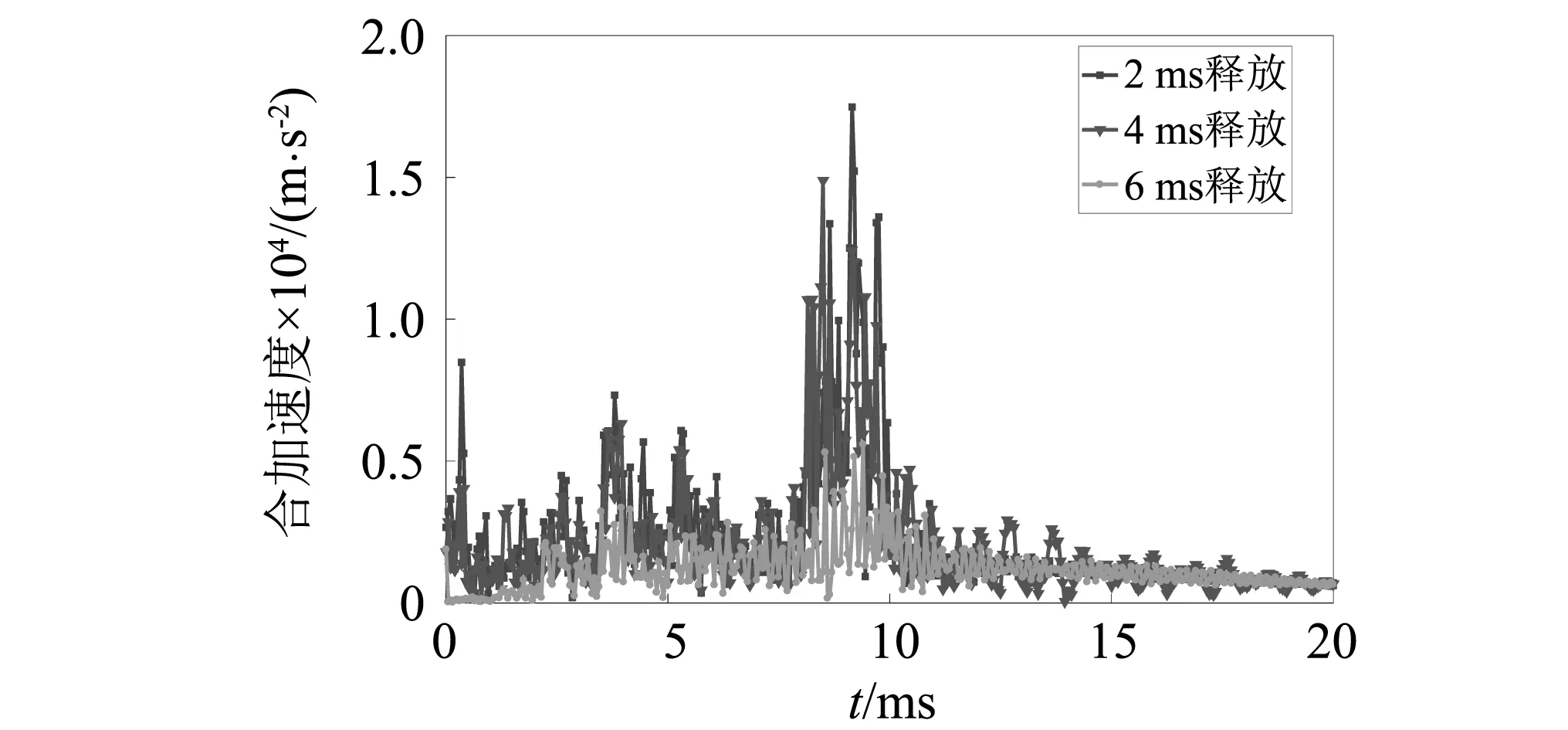
圖12 不同解鎖時間條件下的上端框沖擊加速度響應
4.1 預緊力對包帶分離與捕獲過程的影響
由于預緊力水平直接關系到預緊剛性包帶的彈性勢能總量,因此會對剛性包帶的分離過程產生明顯影響。同時預緊力在剛性包帶靜力學設計中也具有重要地位,需要同時滿足材料強度極限限制和靜力學承載要求。本部分在滿足靜力學要求的預緊力范圍內(20~40 kN),重點研究包帶預緊力對包帶分離與捕獲運動的影響規律。不同預緊力條件下的包帶接頭速度變化規律,如圖13所示。從圖13可知,接頭速度變化規律未發生本質改變,但隨著預緊力逐漸增大,0~2 ms緩釋階段的接頭速度整體呈增大趨勢。緩釋后速度呈現小幅波動式緩慢增大(對應2~6 ms),且波動幅度隨預緊力增大而明顯增大。速度峰值出現時間隨預緊力增大而有所提前,且峰值取值由7.79 m/s提升至10.65 m/s,增加36.7%。在6~20 ms的波動變化區間內,接頭速度的振蕩幅度也同樣隨預緊力增大而增大。
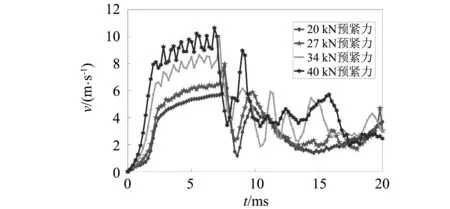
圖13 不同預緊力條件下的包帶接頭速度時間歷程
不同預緊力情況下的包帶與端框和捕獲器的配合時間,如圖14所示。從圖14可知,包帶各典型截面的分離順序會因預緊力不同而發生明顯改變。當預緊力等于20 kN時,包帶按照1#~6#截面順序依次分離,且率先與捕獲器1接觸,與其他捕獲器接觸時刻均延后10 ms以上。當預緊力大于等于27 kN時,包帶按先1#和6#截面再到中間截面順序分離,且包帶與捕獲器接觸時刻均隨預緊力增大而提前。這是由于預緊力越小,包帶儲存的應變勢能越小,包帶中點位置的彈性勢能在緩釋階段得到充分釋放,不能產生較大的分離速度,導致包帶接頭速度明顯大于包帶中點。與解鎖時間增長類似,預緊力過小也可能導致上端框傾斜分離,因此應盡可能提高預緊力幅值。
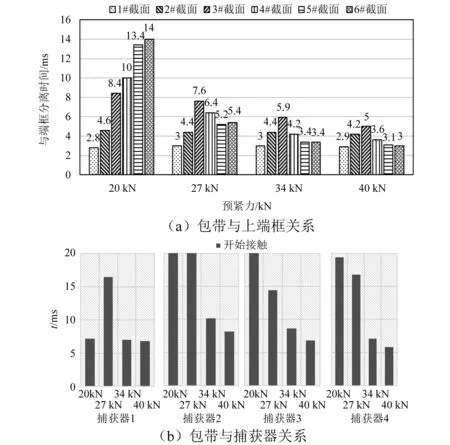
圖14 不同預緊力條件下包帶與端框和捕獲器配合關系
不同預緊力情況下的衛星安裝平面加速度沖擊響應,如圖15所示。從圖15可知,隨著預緊力的增大,沖擊響應也在不斷增大,且峰值出現時間也明顯發生改變,最大沖擊由1.69×103m/s2上升至2.7×104m/s2,提高一個量級。從減小沖擊響應角度出發,應盡量限制預緊力水平,這與改善包帶運動規律相矛盾。

圖15 不同預緊力條件下的上端框沖擊響應時間歷程
5 結 論
本文以應用于重型運載火箭的剛性包帶式星箭連接裝置為對象,建立其完整“安裝-預緊-分離”過程非線性多體動力學分析模型,重點研究剛性包帶分離與捕獲過程中的動力學響應規律及其關鍵影響因素。主要結論如下:
(1)包帶接頭分離速度在緩釋階段速度迅速增大,隨后波動式緩慢增長,直至與捕獲器接觸;包帶接頭和中點位置率先與端框分離和與捕獲器接觸;分離沖擊沿火箭軸線方向迅速衰減。
(2)隨著解鎖時間延長和預緊力減小,包帶接頭分離速度逐漸降低,與捕獲器接觸時刻延后,接觸時長增加,衛星所受沖擊逐漸減小;與脫離端框時間逐漸增大,甚至可能改變包帶分離運動規律,引起衛星傾斜分離。
(3)解鎖時間和預緊力對包帶分離運動和加速度沖擊的影響規律相反,取值過大或過小對包帶分離過程均有不利影響,在工程應用中應給予綜合考慮。

