基于矩量法非對稱平行耦合微帶線濾波器的設計

(景德鎮陶瓷大學機電學院,江西景德鎮 333403)

隨著有線、無線通信技術的發展,微波濾波器在雷達技術、衛星通信、電子對抗、通訊安全等領域得到廣泛應用。微波濾波器的作用是篩選不同頻率的信號,允許系統指定的信號通過,過濾干擾信號。在某些領域中,微波濾波器的性能對整個系統有決定性的作用。

濾波器發揮著日益重要的作用,因此如何精確高效地設計性能優良的微波濾波器得到大量研究。在此背景下各種電磁仿真軟件相繼問世,為設計優化濾波器提供了多種選擇,但是選擇不當會將簡單問題復雜化。電磁仿真軟件有各自的特點,例如 ADS(Advanced Design System)仿真效率高,優化效果好,但是仿真優化過程在相對理想條件下,導致仿真結果與實際情況有較大差異。版圖仿真效率低于ADS,但是其仿真準確性優于ADS,與HFSS(High Frequency Structure Simulator)相比仿真準確性有所不及。HFSS仿真結果精確,但是算法復雜,效率較低。因此如何合理的使用仿真軟件是能否精確、高效設計濾波器的關鍵。

平行耦合線濾波器因具有相對帶寬大、與射頻電路匹配度高等優點,而得到了深入的研究[1-9],其主要研究方法有:軟件分析法[1-8]、傳輸線理論分析法[9],本文選擇軟件分析法。文獻[1-2]設計的濾波器通帶寬、帶內損耗小,但是通帶反射較差,由于其優化全程在HFSS 完成,因此這種方法耗時,效率低。文獻[3]利用ADS 設計了一種五階平行耦合線濾波器,帶內損耗小。文獻[4-5]所設計的平行耦合線濾波器帶內損耗小,但是濾波器選擇性較低。文獻[6]制作了一種四階平行耦合微帶線帶通濾波器,其設計過程在ADS 中優化在版圖中驗證,若不符合要求則返回ADS 再次優化,其過程十分繁瑣耗時。文獻[7-8]闡述了一種基于ADS 高效設計平行耦合線帶通濾波器的方法,但是這種方法依賴ADS 的自動優化,只適用于粗模型仿真得到初始結構參數,若要制作實物,后期仍需要大量時間優化。上述文獻所設計的平行耦合線濾波器存在通帶反射差、阻帶選擇性較低、優化方法不當等問題。

為了提高優化設計濾波器的精確性、效率與阻帶選擇性,本文通過合理的使用電磁仿真軟件,在保證精確性的前提下,提高設計優化濾波器的效率與性能。并設計優化七階平行耦合微帶線濾波器驗證,具體措施如下:一是采用非對稱結構來獲得更好的通帶反射;二是采用矩量法與ADS 聯合仿真優化提高設計優化效率,在版圖中建模,在ADS 中優化,只在HFSS 中進行驗證與微調,保證精確性的前提下,提高設計優化效率;三是增加濾波器的階數,改善其選擇性。

1 設計過程

1.1 耦合微帶線結構參數的計算

本文中設計一個七階平行耦合微帶線帶通濾波器,選擇切比雪夫低通濾波器原型,如圖1 所示。濾波器的技術指標為:中心頻率f0=4.8 GHz,帶寬(1.2±0.2) GHz,帶內衰減≤2 dB,端口反射損耗≥25 dB,3.4 GHz 以下和6.2 GHz 以上的阻帶衰減大于50 dB。選擇基板厚h=1 mm,相對介電常數εr=2.7。設計步驟如下。

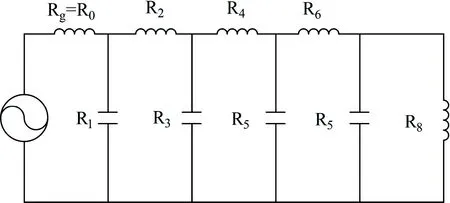
圖1 低通濾波器原型Fig.1 A low pass prototype

(1) 計算歸一化頻率:

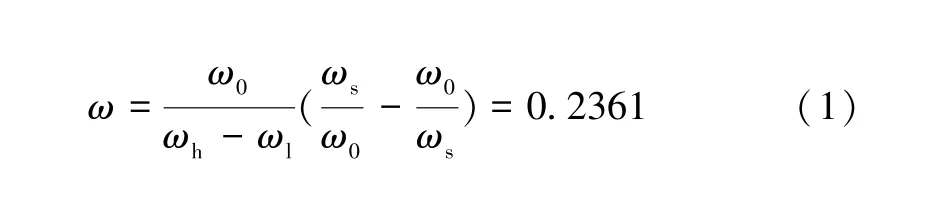
式中:ω0為中心頻率;ωs為帶外頻率;ωh、ωl分別為通帶上邊頻與下邊頻。選擇0.1 dB 波紋的切比雪夫低通濾波器原型,查衰減曲線得N=7,可以滿足阻帶衰減要求。查表得歸一化元件值g0=g8=1.00,g1=g7=1.81,g2=g6=1.42,g3=g5=2.10,g4=1.57。

(2)計算導納變換器的導納值Ji,i+1[10]:

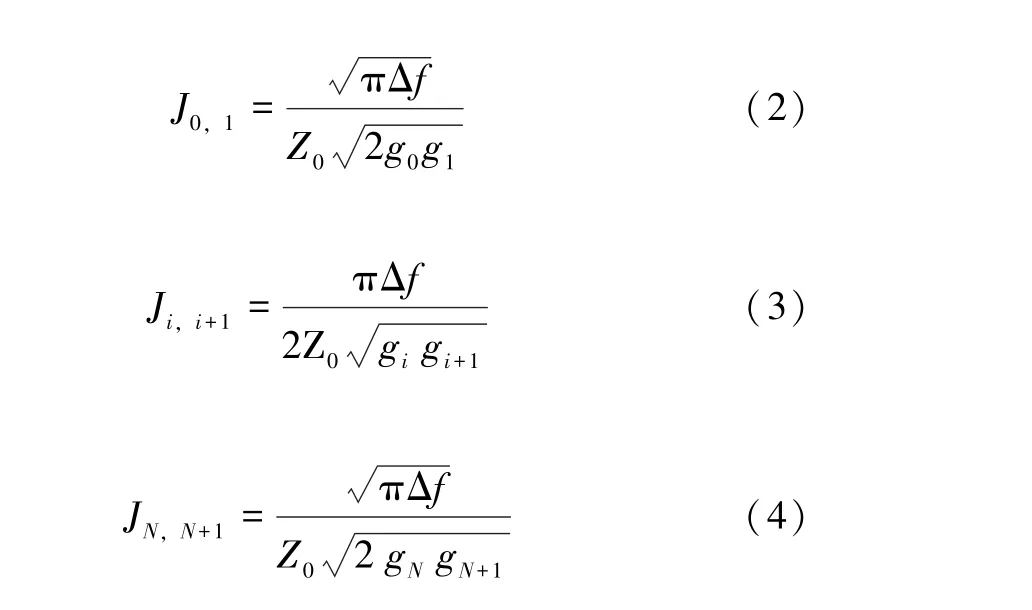
式中:Δf為相對帶寬;Z0是端口的阻抗。

(3) 計算各段耦合線的偶模、奇模的特性阻抗Zoe、Zoo:

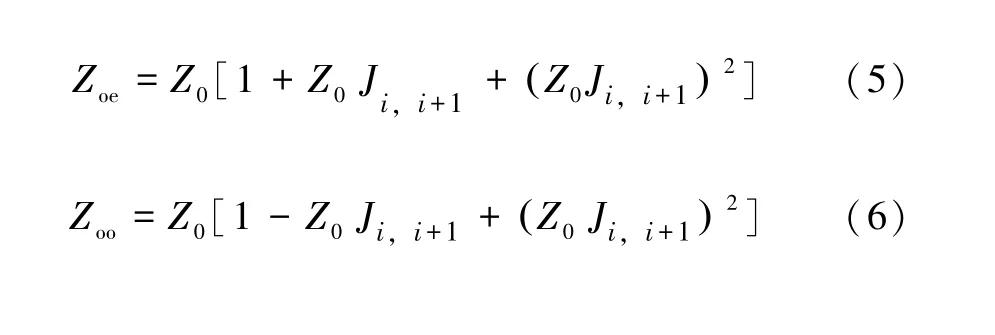
式中:Z0=50 Ω。

(4) 根據基板的參數和奇偶模阻抗,利用ADS 中Line Calc 進行計算,計算結果列于表1 中,wi、si、li(i=1,2,…,8)分別為相應諧振器的寬度、間距、長度,其原理圖如圖2 所示。

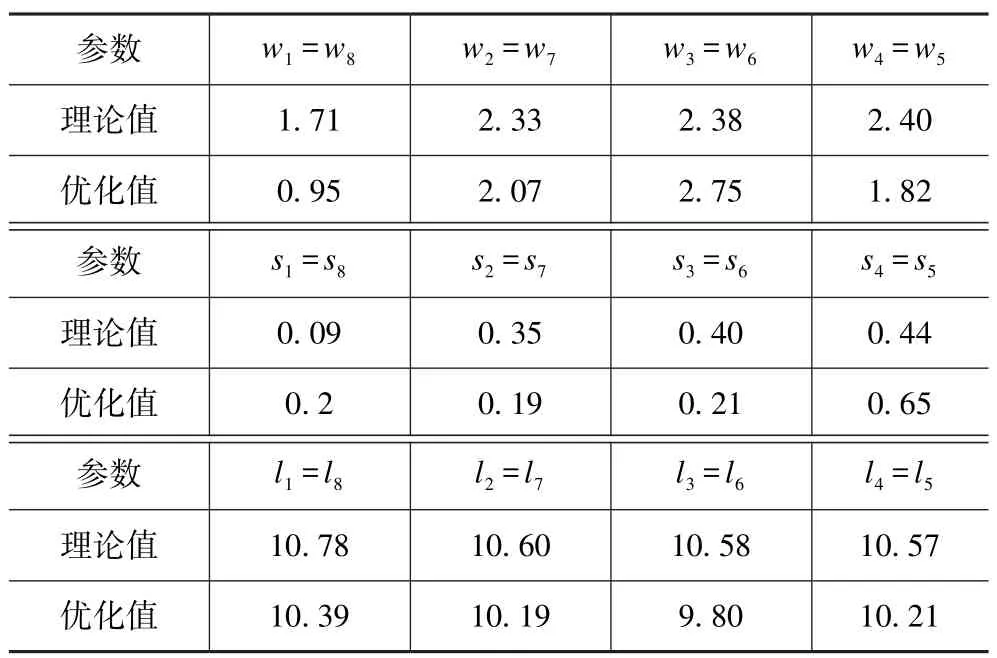
表1 ADS 中濾波器結構參數的理論值與優化值Tab.1 Theoretical and optimal values of filter structural parameters in ADS mm

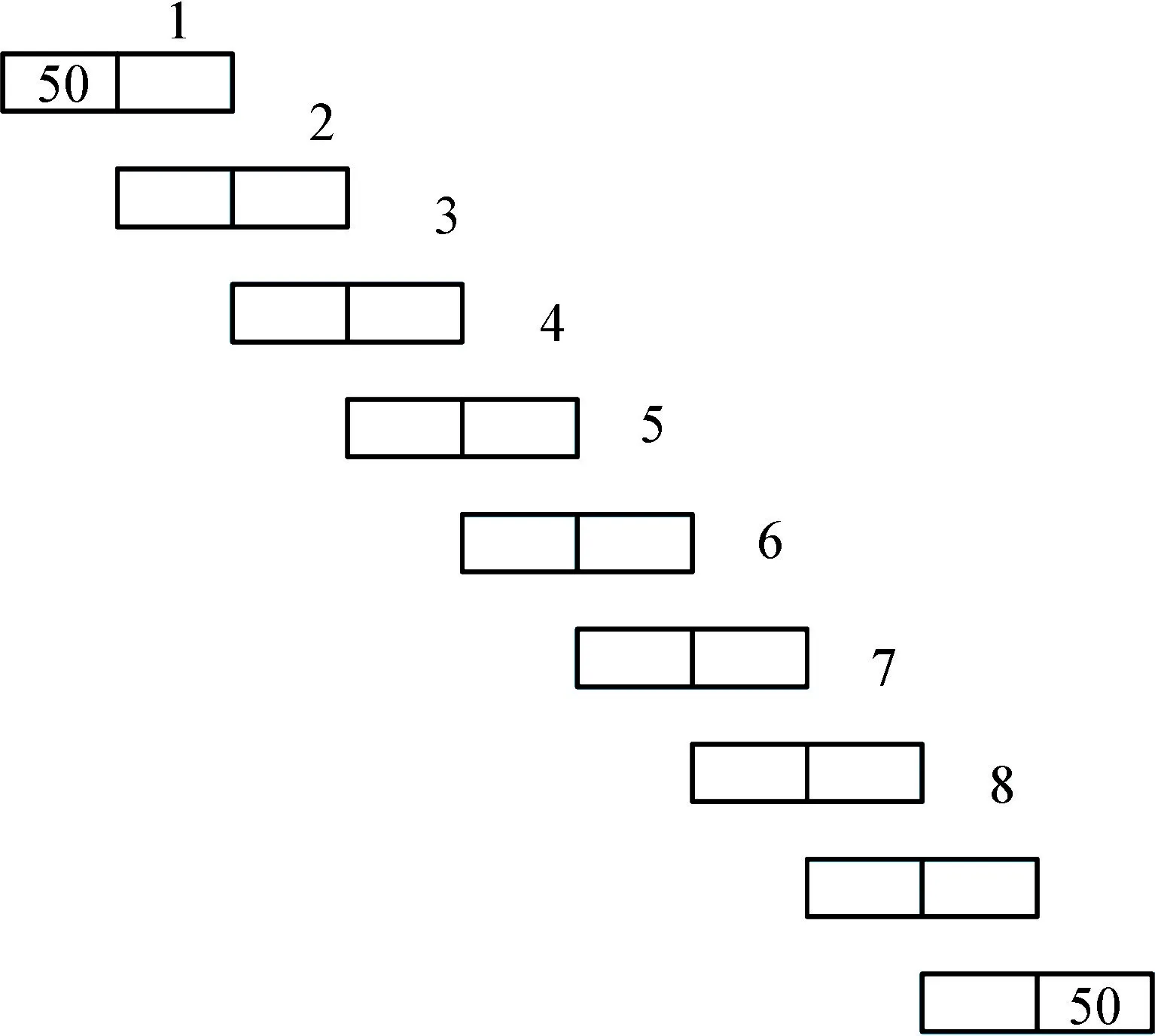
圖2 七階平行耦合微帶線帶通濾波器原理圖Fig.2 Schematic diagram of seventh-order parallel coupled microstrip line bandpass filter

1.2 濾波器的仿真與優化

以表1 中的理論結構參數在ADS 中建模如圖3 所示,并對此模型仿真,仿真結果如圖4 所示,其通帶較理論值窄,反射損耗差,不符合設計要求,因此要對其優化。

采用ADS 自帶的優化功能進行優化,優化后的結構參數也列于表1 中,優化后的波形如圖4 所示。通過圖4 對比可以看出,優化后的通帶與反射曲線均符合設計要求。將優化后的結構參數代入HFSS 驗證,仿真波形如圖5 所示,由圖5 觀察得HFSS 與ADS 仿真結果存在差異,尤其是反射損耗與ADS 仿真結果不符。這是ADS 原理圖仿真沒有考慮到不相鄰微帶線之間的耦合所造成。

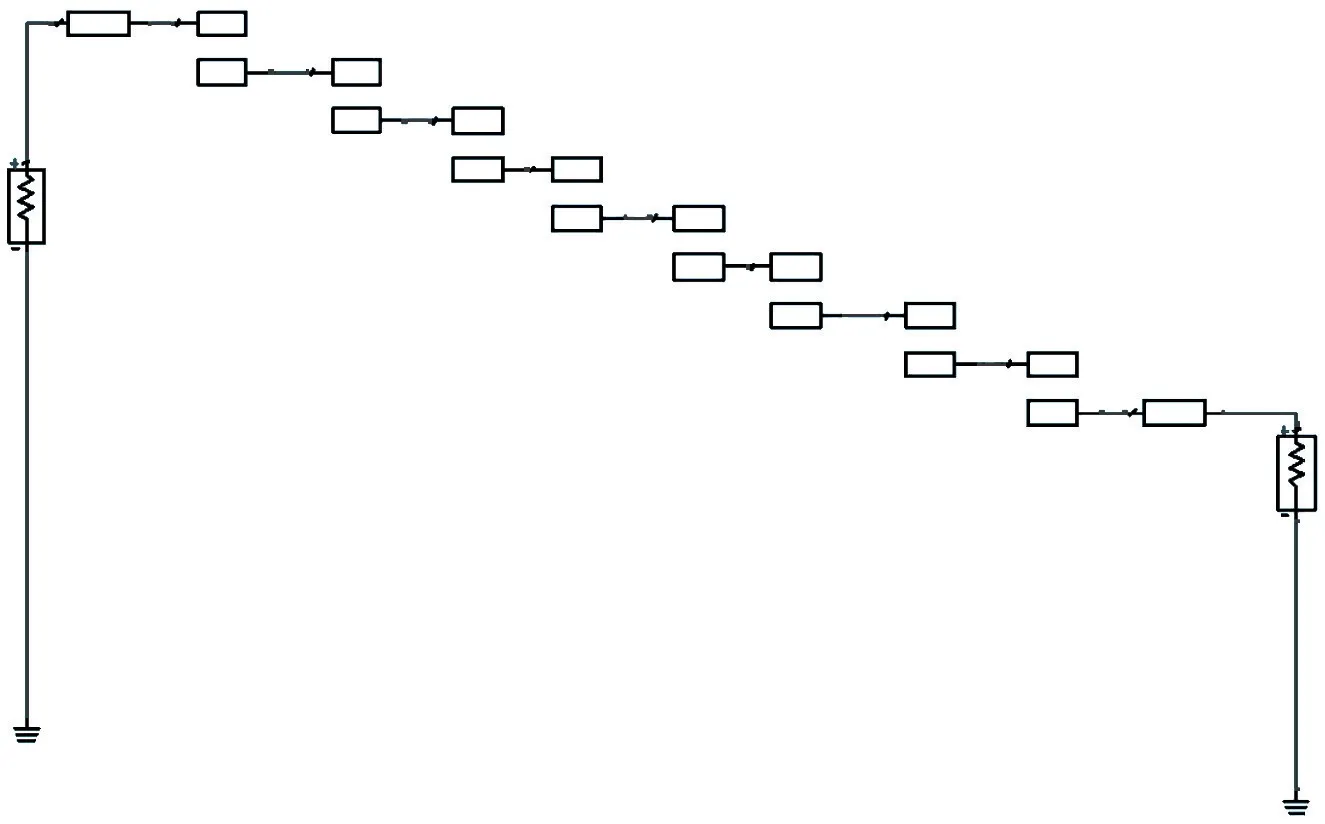
圖3 濾波器在ADS 中仿真模型Fig.3 Simulation model of filter in ADS

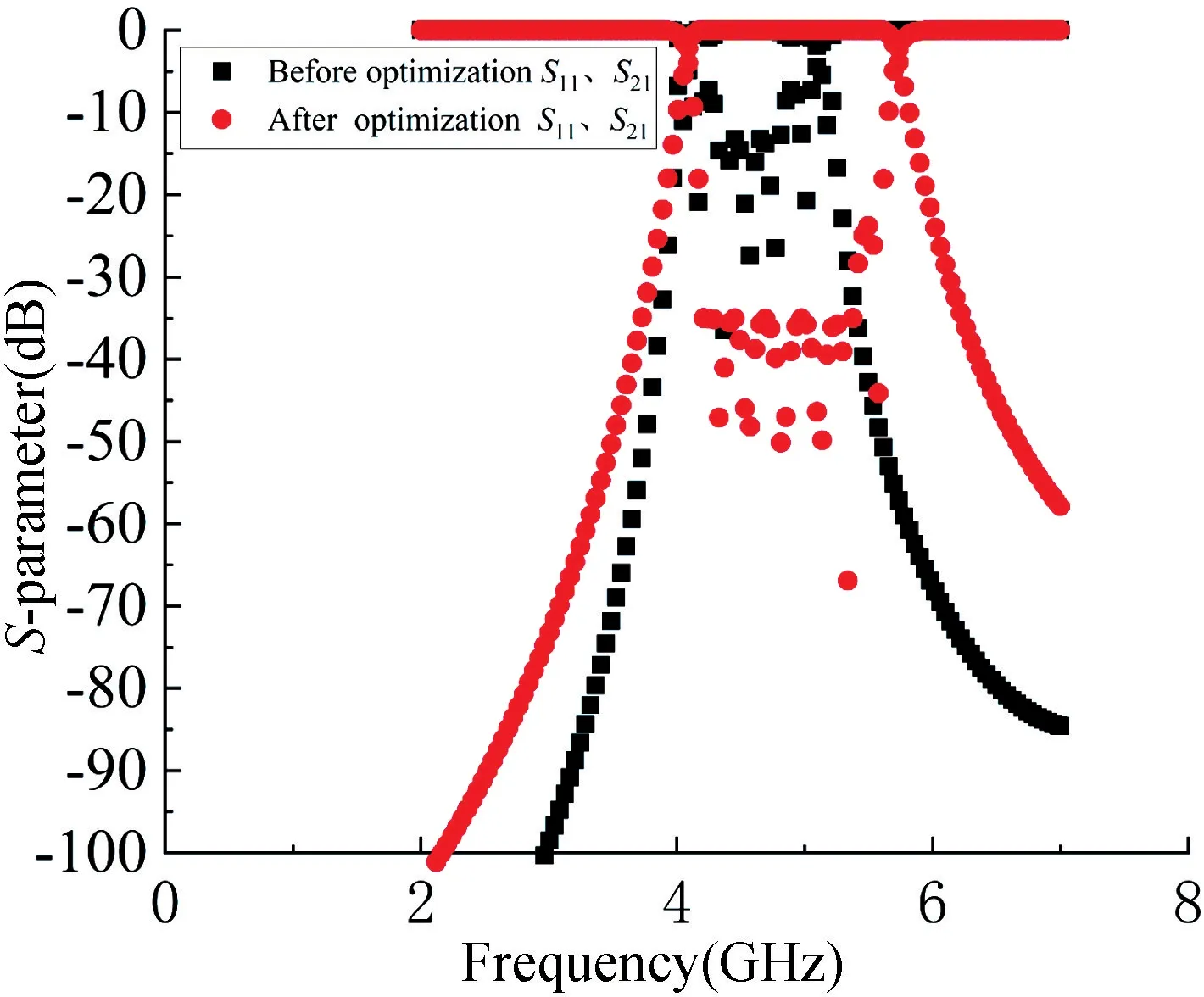
圖4 濾波器在ADS 優化前后的S 參數Fig.4 The S-parameters of filter in ADS before and after optimization

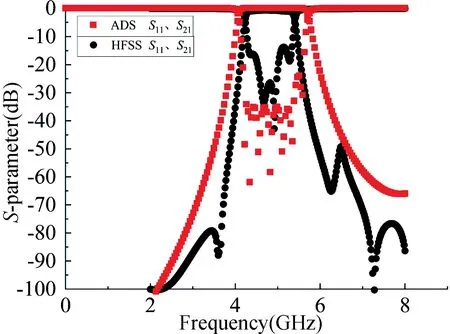
圖5 ADS 仿真結果與HFSS 仿真結果Fig.5 The simulation results of ADS and HFSS

HFSS 精度高,但是算法復雜,耗時多,為了提高優化效率,采用版圖和原理圖聯合仿真優化。在版圖中建模,如圖6 所示,在ADS 原理圖中進行優化仿真,如圖7 所示,圖中的7pole 是圖6 的版圖模型,優化結果如圖8 所示。

圖6 七階平行耦合微帶線帶通濾波器版圖模型Fig.6 Layout model of seventh-order parallel coupled microstrip line bandpass filter

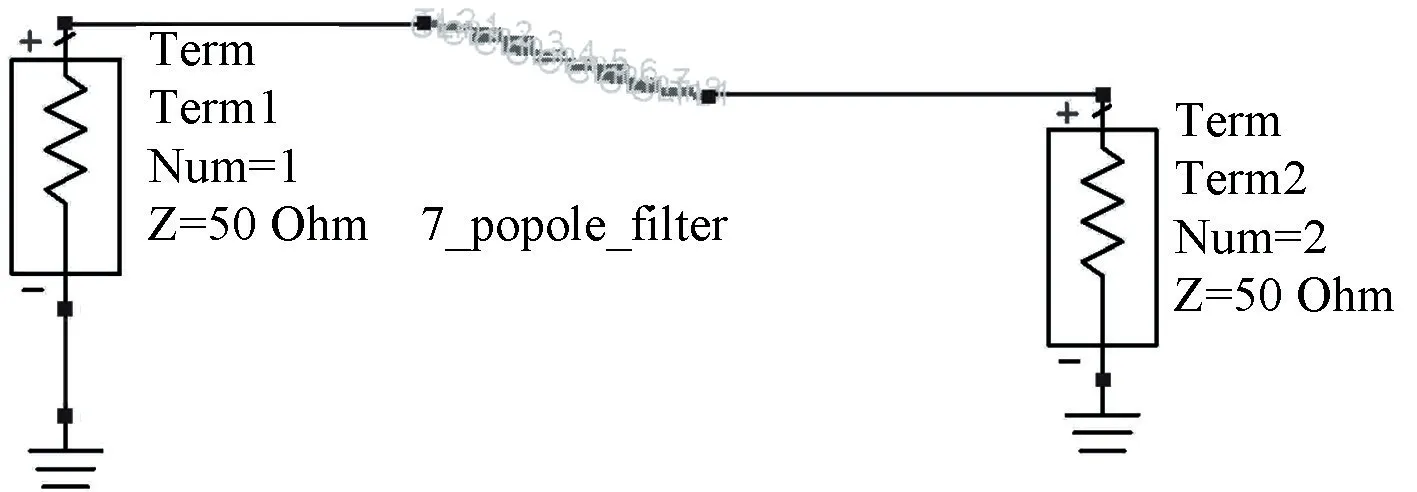
圖7 ADS 中版圖與原理圖聯合仿真Fig.7 Layout and schematic joint simulation in ADS

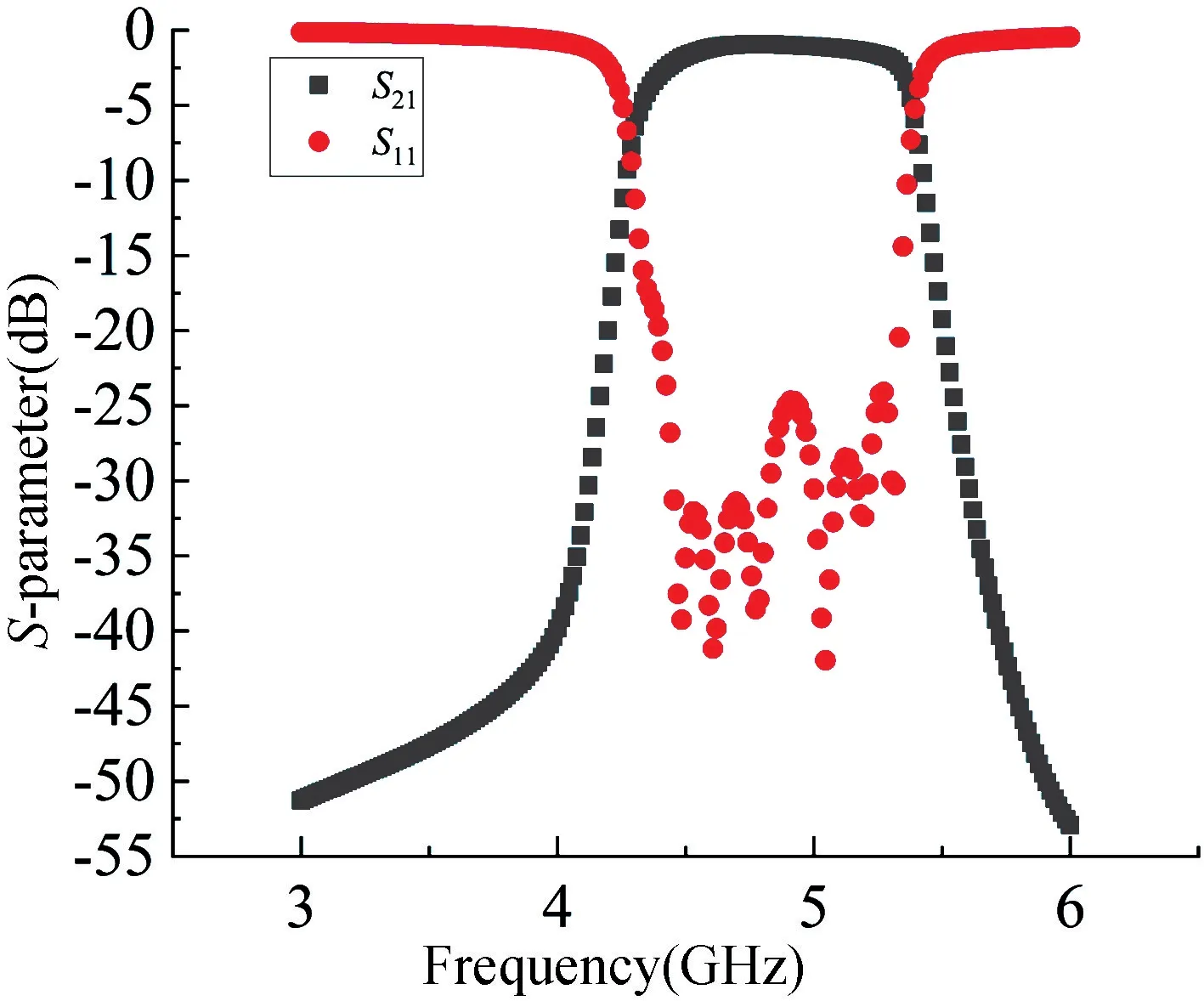
圖8 ADS 中版圖優化仿真結果Fig.8 Layout optimization simulation results in ADS

將優化后的結構參數放到HFSS 中進行驗證,如圖9 所示,性能基本達到要求,僅需微調。版圖仿真是基于矩量法,而HFSS 仿真是基于有限元法,因此兩者仿真會有所差異。版圖優化僅僅只需要2 h 即可達到要求,而HFSS 中仿真一次就需要12 min,優化所需時間長,顯然版圖優化仿真省時,效率高。

在HFSS 中對參數進行微調時發現:li影響中心頻率,隨著li的增大,中心頻率變小,wi影響其損耗,si影響其帶寬,并且隨著si的增大,帶寬變窄。在優化過程中若采用對稱結構很難達到預期要求,反射損耗一直達不到理想要求,于是采用非對稱結構,對參數進行微調。采用非對稱結構并運用上述規律,對濾波器進行優化,考慮制作工藝,將參數精度調整到0.01 mm,結構參數如表2 所示。從表2 可以看出,濾波器的結構不完全對稱,即w1≠w8,w2≠w7,…,l3≠l6。仿真結果如圖10 所示,濾波器已達到設計要求,并且獲得比較好的性能。綜上所述,采用不對稱結構可以提高濾波器的反射性能。

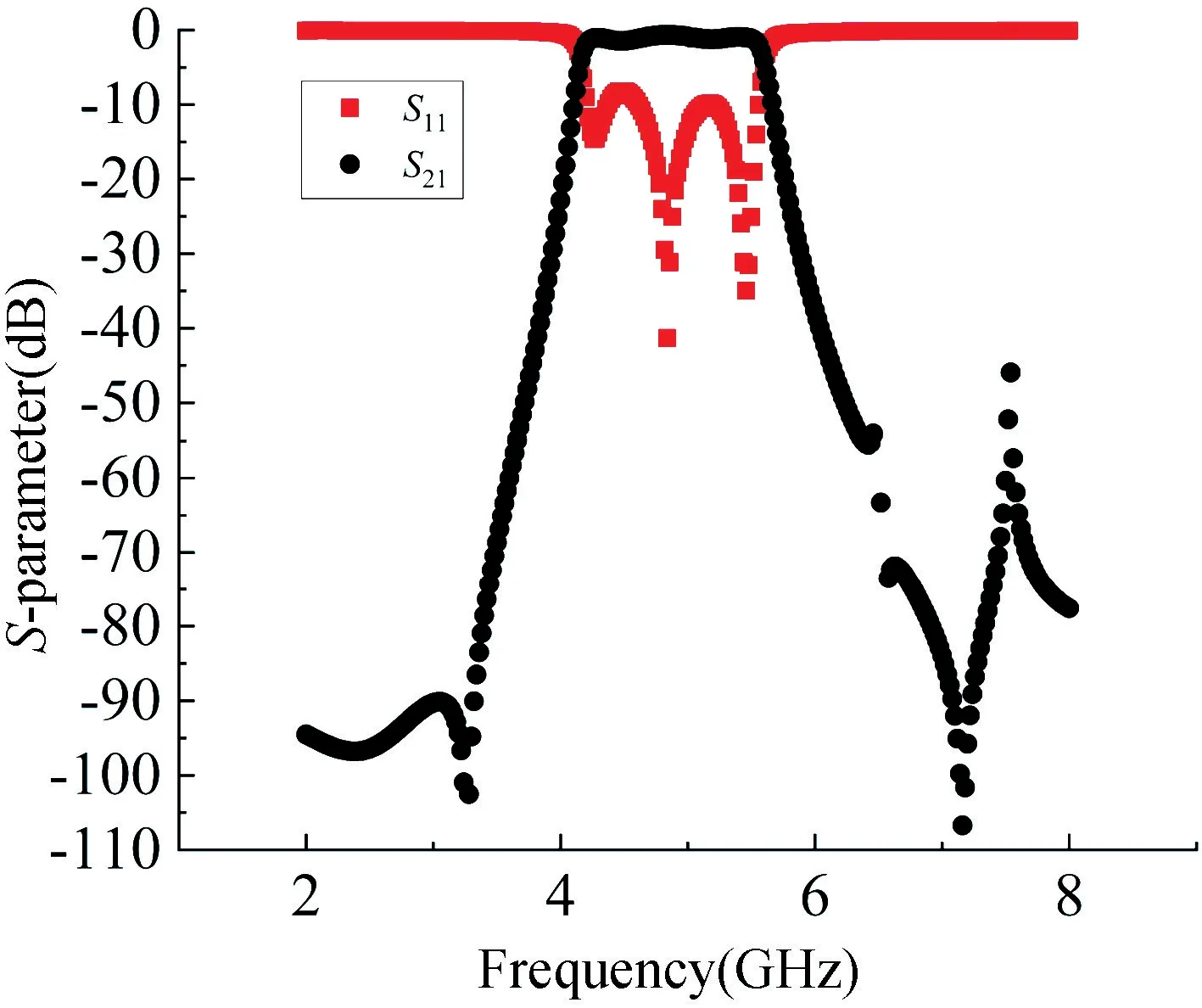
圖9 版圖優化后HFSS 驗證結果Fig.9 HFSS verification results after layout optimization

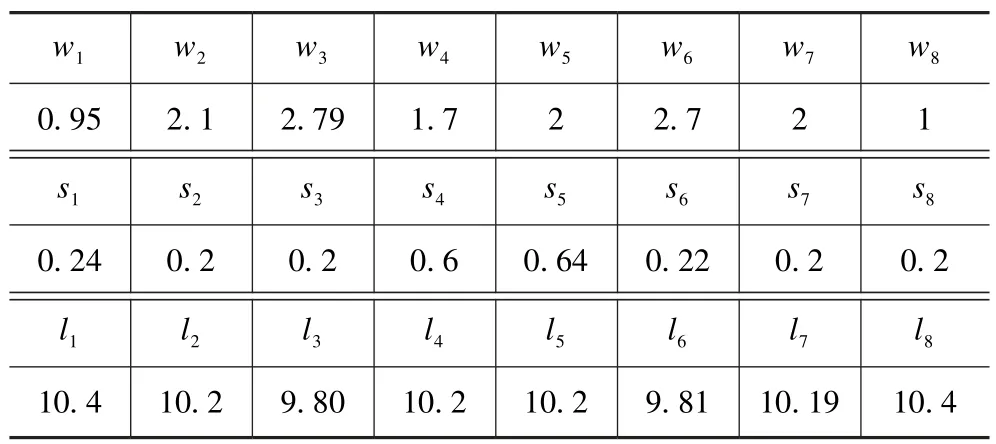
表2 優化后各結構參數Tab.2 The optimized structure parameters mm

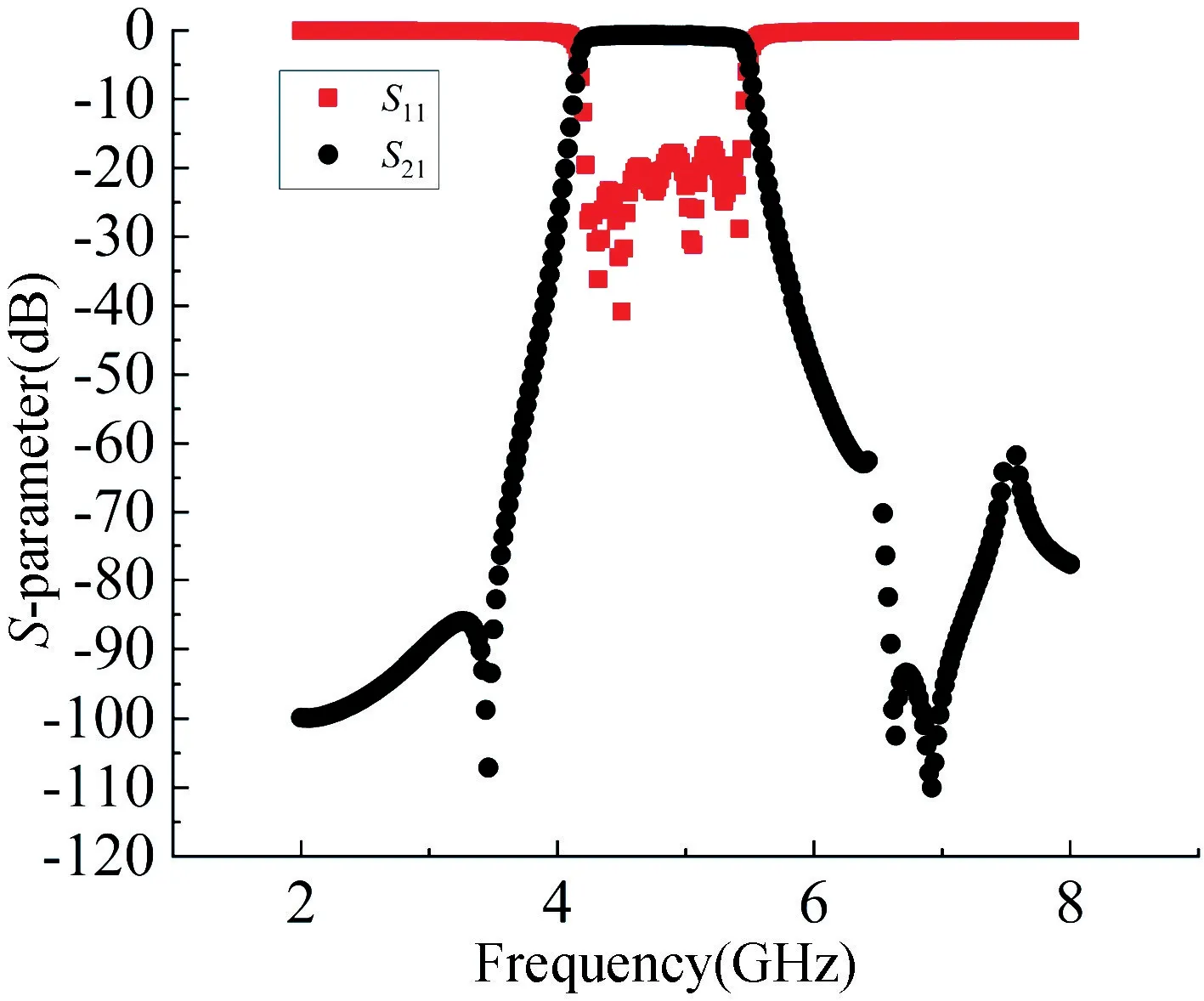
圖10 HFSS 優化后仿真結果Fig.10 Optimized simulation results of HFSS

2 實物的制作與測量

以表2 的結構和尺寸制作實物,實物照片如圖11所示。用網絡分析儀Agilent E5071B 進行測量,測量數據如圖12 所示,中心頻率為4.86 GHz,帶寬BW=1.2 GHz,插入損耗為1.2 dB,反射損耗大于25 dB,3.4 GHz 以下和6.2 GHz 以上的阻帶衰減均大于50 dB。測量結果與仿真結果相比,除中心頻率偏高外,其余均相符。

圖11 七階平行耦合微帶線帶通濾波器實物照片Fig.11 The photo of the seventh-order parallel coupled line bandpass filter

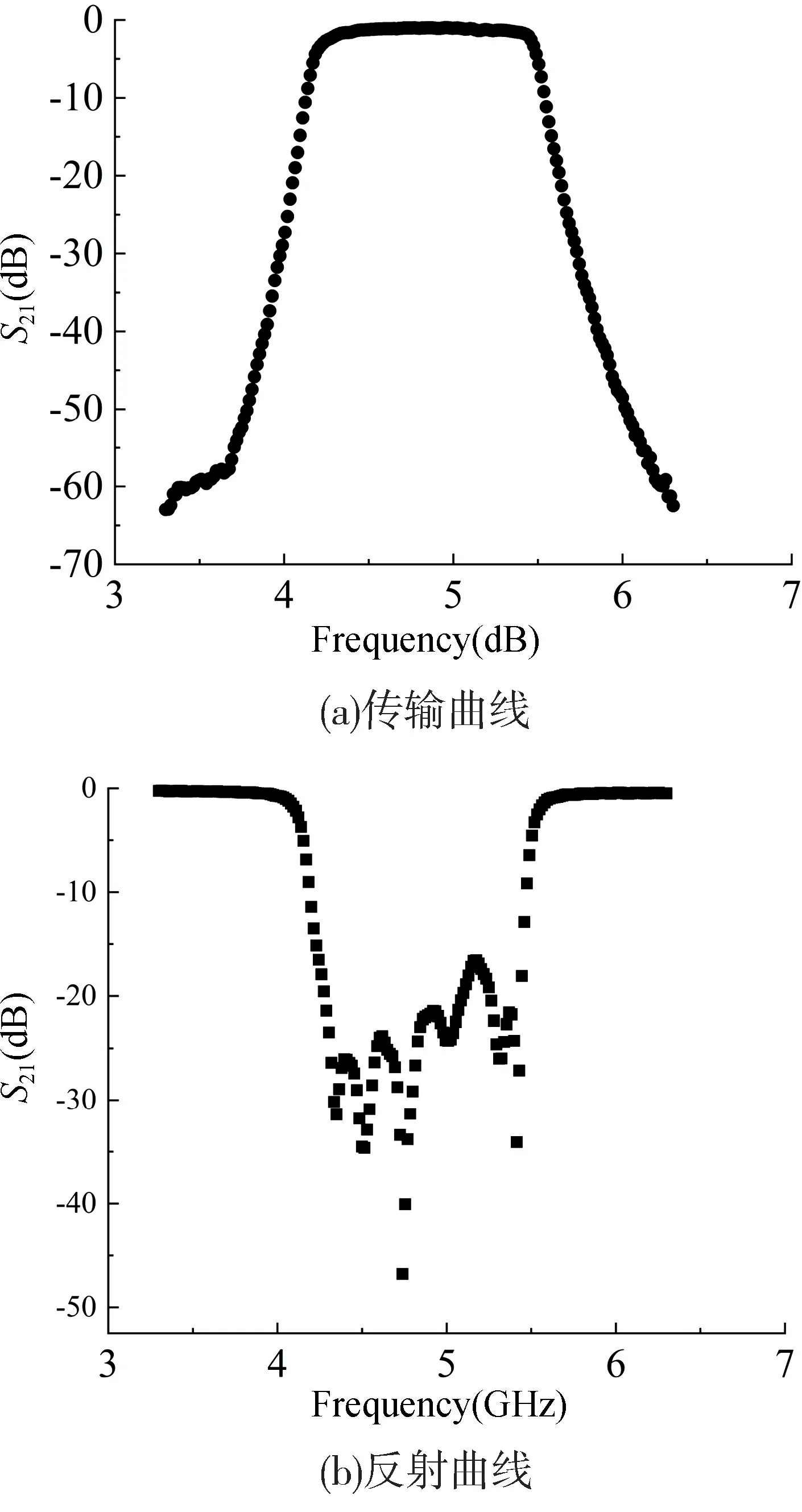
圖12 七階平行耦合線帶通濾波器實測曲線Fig.12 The measured curves of the seventh-order parallel coupled linebandpass filter

表3 列出了本文的測量結果與其他文獻所報道的結果,從表中看出,本文的濾波器的插入損耗小、反射特性好,矩形系數高。

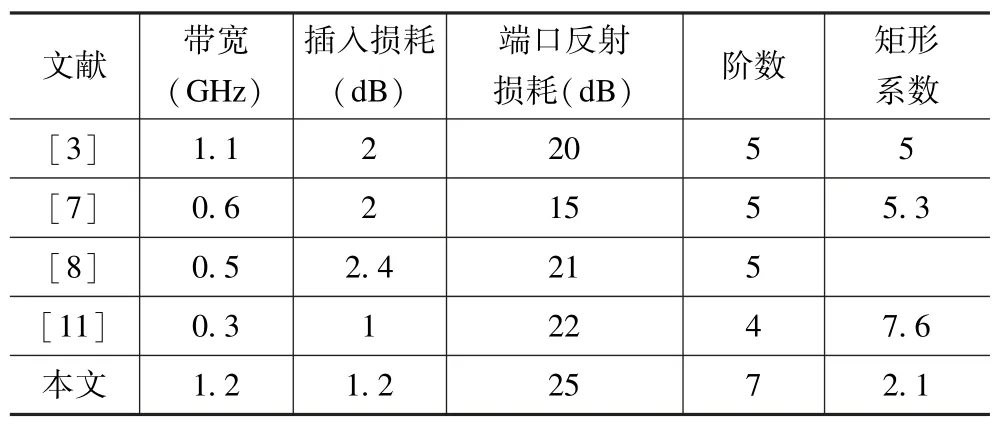
表3 與其他平行耦合微帶線帶通濾波器性能對比Tab.3 Compared with other parallel coupled microstrip line bandpass filters

3 結論

提出一種濾波器的設計方法:在版圖中建立模型,將模型放到ADS 原理圖中進行仿真優化,然后在HFSS 中進行驗證微調。該方法結合ADS 原理圖仿真優化的省時高效與版圖仿真的準確性,大大提高了濾波器設計與優化的效率。并用此方法設計制作了七階平行耦合微帶線濾波器,實驗驗證了矩量法的可行性與高效性,且驗證了非對稱結構對改善濾波器的性能有良性作用。該方法與結構可應用到其他微波元器件的設計中。