基于正交分析的地鐵目標頻段隔振排樁參數研究

姜博龍

(中國鐵路設計集團有限公司城市軌道交通數字化建設與測評技術國家工程實驗室,天津 300308)

排樁屏障被認為是軌道交通環境振動路徑隔振中的一種有效方式，因而被廣泛研究[1-3]，其隔振效果影響因素包括樁徑、樁間凈距、土層與樁的材料參數、樁長、樁的布置范圍、樁的埋深與地鐵埋深的相對關系等。近年來，周期結構帶隙理論被引入到排樁隔振的研究中，為目標頻段的隔振排樁設計提供了理論基礎[4]。

大量學者圍繞目標頻段隔振的周期排樁展開研究。黃建坤[5]將該問題簡化為二維平面應變問題來研究體波的傳播衰減規律，進行了無限周期假設和周期邊界處理，求解得到樁-土周期系統的頻散關系，揭示了首階完全帶隙隨樁徑、樁間距、樁與地層材料參數等因素的變化規律；劉心男[6]將三維有限元計算結果與二維平面應變模型計算結果對比，發現隨著樁長的增加，二者計算結果逐步接近；蒲興波[7]提出了全新的面波頻散曲線識別方法；另外，還有部分學者圍繞復阻尼周期排樁[8]以及飽和土條件下周期排樁[9]展開研究。目前，已有原理性實驗驗證了周期排樁帶隙分析理論的正確性[10]，證明在采用無線周期排樁求解的帶隙頻率范圍內與之對應的有限周期排樁會對振動產生大幅衰減；另外，地鐵-地層-周期排樁三維有限元模型被建立來預測設計排樁在相應帶隙頻段內阻隔地鐵振動的效果[11]；此外還有研究涉及優化選型方法[12]等。

目前隔振排樁隔振效果研究中針對地下隧道振源的、可以設計調節隔振頻段的研究并不多。基于帶隙特性的周期排樁設計頻段內的隔振性能研究主要分為無限周期排樁帶隙特性和有限周期排樁傳輸衰減特性。由上述分析以及表1可以看出，在帶隙特性研究中廣泛采用的無限周期、無限樁長假設，明確了帶隙隨樁徑、樁間凈距、樁與地層材料的變化規律，但是對樁長、樁的布置數量以及振源與樁相對位置關系等問題研究得不夠充分，而這些因素將直接決定計算帶隙范圍內振動的實際衰減情況，包括排樁屏障后有效衰減區域以及不同區域的振動衰減水平。此外，上述因素對隔振效果影響的強弱順序、設計取值亟需參數化分析，提供相應的理論依據。本文基于正交理論[13]、帶隙理論和數值模型，針對地下振源，對影響有限周期排樁帶隙范圍內振動衰減效果的因素進行參數研究，包括樁排數、樁列數、樁長、樁到地鐵水平距離、樁與地鐵埋深相對位置關系等，獲得各因素作用主次順序以及在某種典型地層條件下的建議取值。

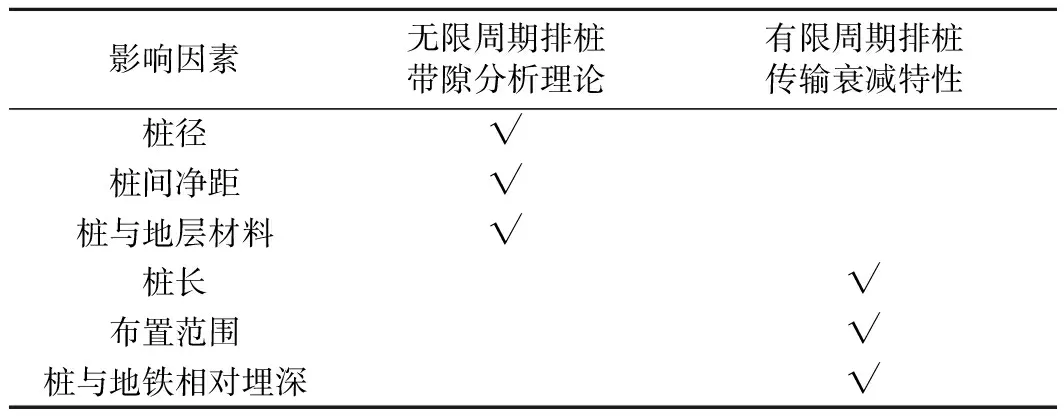
表1 排樁影響因素及對應研究方法

1 周期排樁頻散計算的平面波展開法

1.1 平面波展開法

平面波展開法[14]可用于求解周期排樁帶隙特性，其基本假設包括無限周期假設和無線樁長假設，此時振動在排樁-土層中的傳播可視為平面應變問題，并解耦為平面內問題和出平面問題。不失一般性，波動方程可表示為式(1)的形式

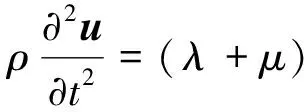
(1)

式中,ρ為密度；λ和μ為拉梅常數；u為位移矢量；uj表示位移分量。

其中,u=[ux，uy，uz]

j=x，y，z

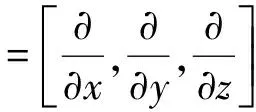
由于排樁的周期性排列，密度ρ和拉梅常數λ和μ可按照傅里葉級數展開為

(2)

式中，G1為倒格矢；r為位置矢量。

其中，f=ρ(r)，λ(r)或μ(r)，r=(x，y，z)

根據Bloch-Floquet理論，位移解可展開為：

(3)

式中，K為波矢；G2為倒格矢；ω為角頻率；u(r，t)為位移矢量。

把方程(2)和方程(3)代入方程(1)，可得到本征方程

(4)

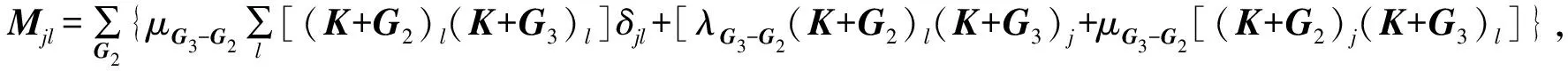
G3=G2+G1;

i，j，l=x，y，z。

對于散射型排樁，傅里葉系數可表示為

(5)

其中，

η=(πR2)/S

(6)

式中，η為單個基本單元中樁的占比；P(G1)為結構函數；S為典型單元面積；J1為第一類第1階貝塞爾函數。

使波矢K掃掠第一不可約Brillouin區，即得到排樁-土體體系的頻散曲線和帶隙。

1.2 計算算例

排樁布置形式及基本單元見圖1，其中，a=4 m、R=1.2 m、r=0.8 m。粉質黏土(圖1(b)中A)密度為2 010 kg/m3，動彈性模量為308 MPa，動泊松比0.327，阻尼比0.03，壓縮波速472.6 m/s，剪切波速235.0 m/s。樁體的材料參數見表2。計算帶隙如圖2所示。

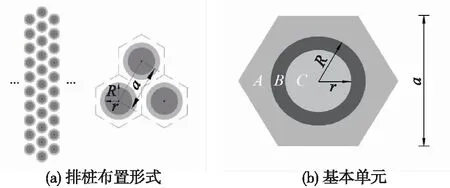
圖1 排樁布置形式及基本單元

表2 排樁材料參數

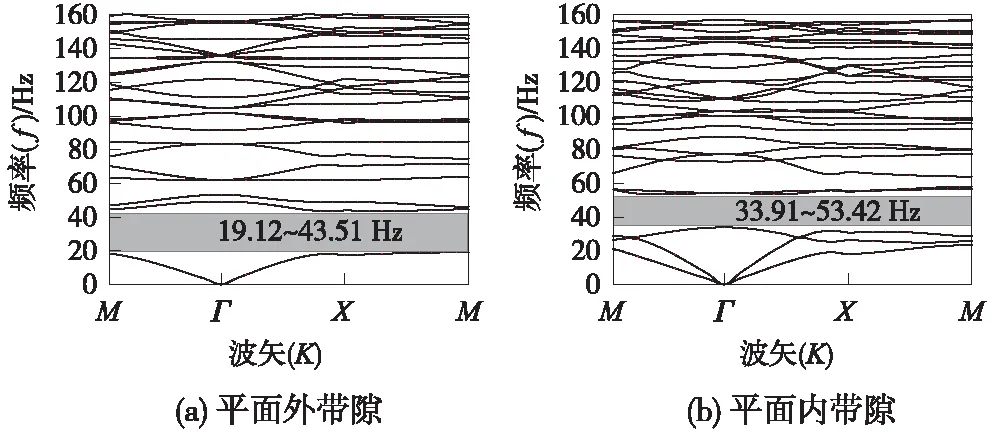
圖2 帶隙分布

2 采用正交分析的參數研究

由上文可知，對于樁-土周期系統的帶隙分布直接相關的參數包括樁徑、樁間距、樁與土的材料參數，文獻[5]已對其進行了參數化分析。由于帶隙分析采用了無限周期、無限樁長的基本假設，因此，忽略了樁長、列數、排數、排樁到隧道水平距離、隧道埋深等5個因素影響，本文采用正交分析方法對這5個因素展開參數分析。本文正交分析所采用的土體信息、樁的排布形式與參數取自上文計算算例，帶隙分布見圖2。

2.1 相關因素選定

設計帶隙頻段內振動衰減水平以及屏障后衰減的有效空間受樁長、列數、排數、排樁到隧道水平距離、隧道埋深等5個因素影響。因此，本節開展5因素、4水平的標準正交分析。

2.2 確定水平

根據周期帶隙理論，每一排隔離樁對振動都有一定的衰減作用，隨著周期復現，最后達到對某些頻段完全濾波的目的，從而形成帶隙，即樁排數越多，隔振效果越好。然而，考慮工程實際的施作空間及成本限制，很少見到5排及以上排樁，故本次正交分析中樁的排數選取的4個水平為1、2、3、4排。

列數并無嚴格的限制，本文采用的4個水平為10、8、6、4列。

根據《鐵路隧道設計規范》[15]和《地鐵設計規范》[16]，振源深度的4個水平選取為0 m(地表情況)、6 m、12 m、18 m，其中0 m為地表振源、6 m為常規淺埋隧道，二者具典型性，其余水平按照增量原則設計。

樁長取1～6倍隧道埋深，并按照等差遞增，樁長設計為12，24，30，36 m。

依照《環境影響評價技術導則—城市軌道交通》[17]，7.5 m是環境振動的一個轉折距離，將其設為排樁到隧道距離的一個水平。壓縮波VP、剪切波VS、瑞利波VR波速關系[18]如式(7)所示

(7)

可得本算例中土層瑞利波速VR=204.9 m/s，關心頻段(帶隙)介于20～80 Hz，土體波長LR介于2.25～10.245 m。泊松比μ=0.327<0.35，隸屬較硬土質，排樁到振源距離r=1.0LR，特征因數ar=2π[19]。

因此，選取排樁到隧道的水平距離為2，7.5，15，22.5 m，遠近場均有涉及。

2.3 選用正交表

正交分析采用標準正交表L16_4_5，即5因素4水平共16次試驗。根據因素與水平，給出有限元計算的具體方案，見表3。

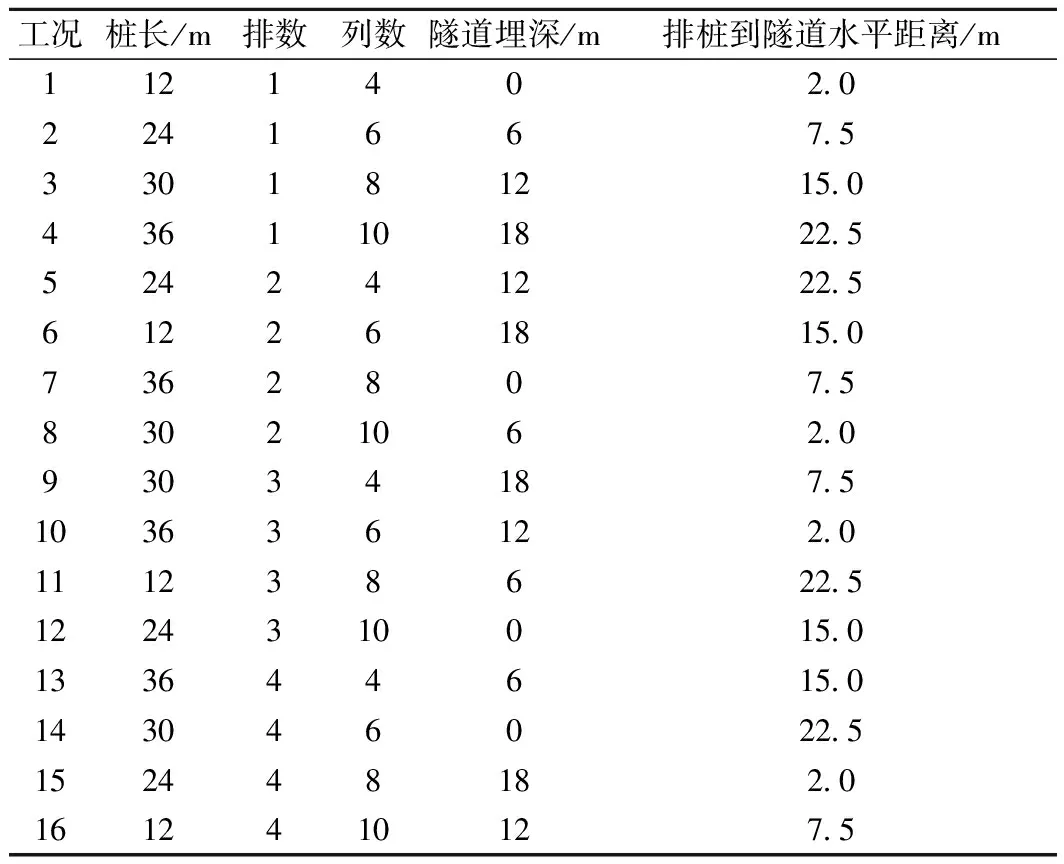
表3 正交分析計算工況

2.4 實施方案

按照設計的正交工況，每組工況計算有樁和無樁兩個模型，參數設置相同。

首先，建立隧道-土體-有限周期排樁動力有限元空間模型。由前文可知，首階帶隙主要分布在19～54 Hz頻段，土體剪切波速為Vs=235 m/s，故λs，max=12.37 m，λs，min=4.35 m。當荷載位置到邊界距離D=1.5λs，max=18.56 m時位移收斂結果較好，當網格尺寸R=λs，min/6=0.725 m時，除靠近荷載0.5λs，min=2.175 m距離外，其余位置計算結果較為理想。本文計算模型范圍取為85 m(長)×40 m(寬)×36 m(高)，振源距左邊界18 m，隧道內外徑分別為5.4，6 m，基底厚0.36 m。左邊界網格尺寸為1 m，隧道與排樁區附近網格尺寸取0.5 m，其他部分采取過渡尺寸網格。按照16種工況的設計參數建立16個模型，并建立16個對應的無樁模型對比，共計32個模型。圖3給出了工況16有樁條件下計算模型。

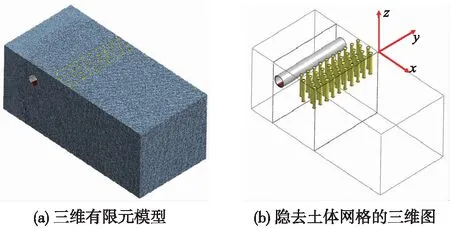
圖3 正交分析中工況16的三維有限元計算模型

土體阻尼比取0.03，分析頻率1～100 Hz。瑞利阻尼常數α和β分別為：α=0.37，β=9.46×10-5。采用彈簧阻尼邊界來解決動力分析中截斷邊界的波動反射，按照法向和切向兩個方向添加。因僅考慮排樁隔振效果與帶隙范圍內的隔振表現，模型采用脈沖荷載作為激振輸入，可節約計算時間且不影響減振效果隨參數變化的作用規律，具體時程和頻譜參見圖4，力的作用點為隧道內道床板上表面的中心點，如圖5所示。

圖4 激勵力的時程和頻譜

圖5 激勵力作用點

2.5 分析指標

本研究的評價量應能夠同時反映帶隙頻段振動衰減水平以及有效衰減區域兩項結果，故定義有限周期排樁首階帶隙中心頻率處的分析指標ER作為評價量

(8)

其中

Arn=a有樁/a無樁

式中，δn為樁后區域某點無樁條件下的加速度響應；δp為樁后區域某節點有樁條件下的加速度響應；SR為積分域，即樁后有衰減的區域；Sn、S為節點所占面積；Arn為節點振幅衰減系數；a有樁為減振工況下排樁后節點的振動加速度響應；a無樁為未設置隔振排樁的對比工況下相同位置節點的振動加速度響應；n為節點數。

評價量ER綜合反映隔振排樁后區域內有效衰減范圍和衰減水平兩項內容，ER越大表明衰減效果越佳。本文對樁后地表一定范圍進行振動提取，考慮邊界效應，提取范圍與邊界保持一定距離，取40 m(y方向)×45 m(x方向)，如圖3所示。計算該范圍首階帶隙的中心頻率振幅衰減系數，將其繪制成云圖，由云圖求解評價量ER，分析評價量ER隨各因素的變化規律。

2.6 結果分析

(1)直觀分析

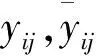
Ri=max[yi1，yi2，…]-min[yi1，yi2，…]

(9)

表4給出了16組正交工況中豎直方向的ER，表5給出了豎直方向ER的極差Ri，并將豎直方向ER結果繪于圖6，極差Ri繪于圖7。水平方向亦同，僅給出極差結果，繪于圖8。由圖7和圖8可知，各因素對豎向振動衰減影響的主次順序：隧道埋深>樁長、排數>列數>排樁到隧道的距離；對水平向影響的主次順序：排樁到隧道距離>隧道埋深、排數>樁長>列數。

表4 各工況豎直方向ER計算結果 m2

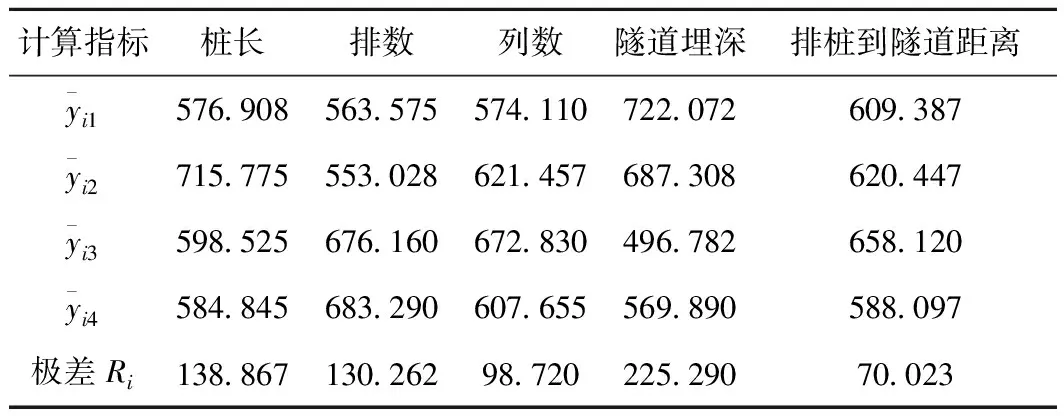
表5 指標ER豎直方向影響因素極差分析結果 m2

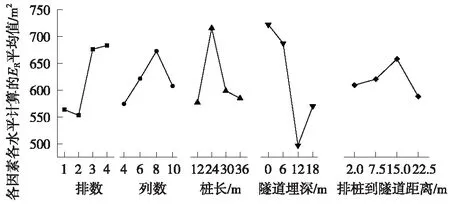
圖6 豎直方向效果曲線

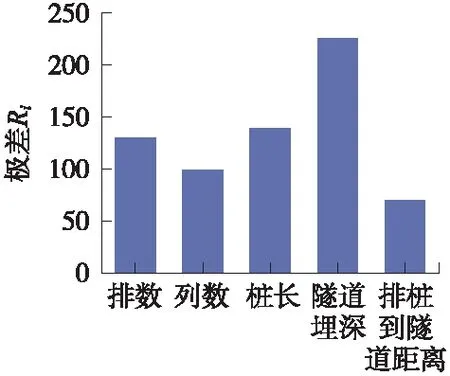
圖7 豎直方向極差柱狀圖

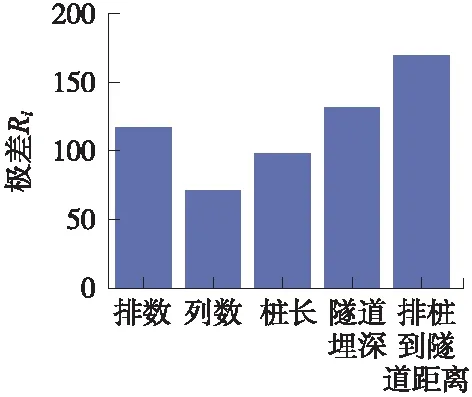
圖8 水平方向極差柱狀圖

(2)方差分析

方差反映數據離散程度，可衡量試驗條件穩定性，根據Fisher偏差平方和加和性原理，在偏差平方和分解的基礎上依托F檢驗法，對影響效果及其交互效果進行分析，此方法稱為方差分析[20]。將方差分析結果列于表6和表7，并將F比值繪于圖9。

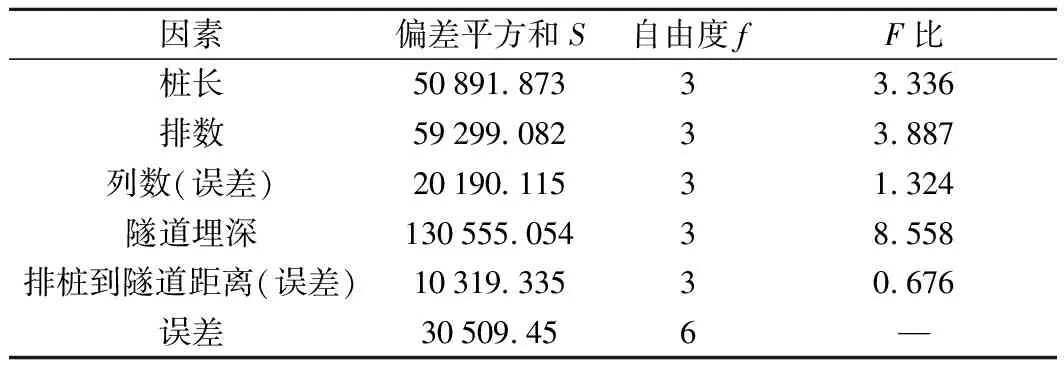
表6 豎直向方差分析

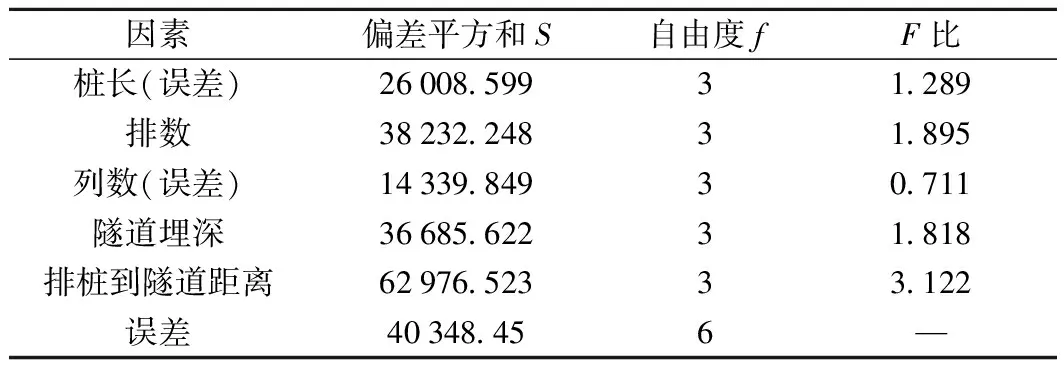
表7 水平方向方差分析

圖9 F比

根據方差分析理論，由表6、表7和圖9可知，在豎直向，隧道埋深對隔振效果的影響最顯著；水平向無顯著性影響因素，但相對來說排樁到隧道距離影響較大。

豎直方向，各因素對隔振效果影響排序為：隧道埋深>排數>樁長>列數>排樁到隧道距離；水平方向順序為：排樁到隧道距離>排數>隧道埋深>樁長>列數。這與直觀分析結果一致。

(3)交互分析

交互作用指因素的聯合作用對結果的影響，它表征因素間相互促進或相互抑制的作用[20]。正交分析中，交互作用記作A×B，原則上交互作用應當作一個因素看待。為研究直觀分析和方差分析中顯著因素(豎直方向包括振源埋深、排數、樁長，水平方向包括振源距排樁距離、排數、振源埋深)間兩兩因素的交互作用，故拆分成多張3因素2水平標準正交表，其中第3個因素為前2個因素的交互作用。如當排數參與交互作用分析時，可選水平組合為(1排、2排)或(2排、3排)或(3排、4排)的3種方式，便可覆蓋全部水平。

兩因素交互有3×3=9種組合，表8和表9分別給出豎直方向排數-隧道埋深交互分析的9種組合中1種的設計表和極差結果，圖10給出了結果柱狀圖。涉及其他因素組合時情況類似，在此不再贅述，僅將主導因素匯總表整理給出，詳見表10～表15。分析過程中，為使體波傳播規律不失一般性，有關長度、距離物理量全部以帶隙中心頻率所對應的土體的體波波長λ作為參照量進行無量綱化，給出相對樁長、相對距離及相對埋深。其中，豎直方向以首階帶隙中心頻率fV=31 Hz對應土體SV波長λSV(λSV=VS/fV=7.58 m)為參照量；水平方向同理取土體的SH波長λSH(λSH=VP/fH=10.74 m)為參照量。

表8 豎直方向隧道埋深(0、6 m)與排數(1、2排)交互作用極差分析結果 m2

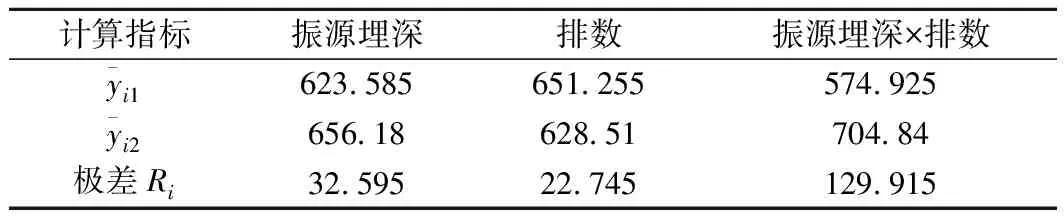
表9 豎直方向隧道埋深(0、6 m)與排數(1、2排)交互作用極差分析結果 m2

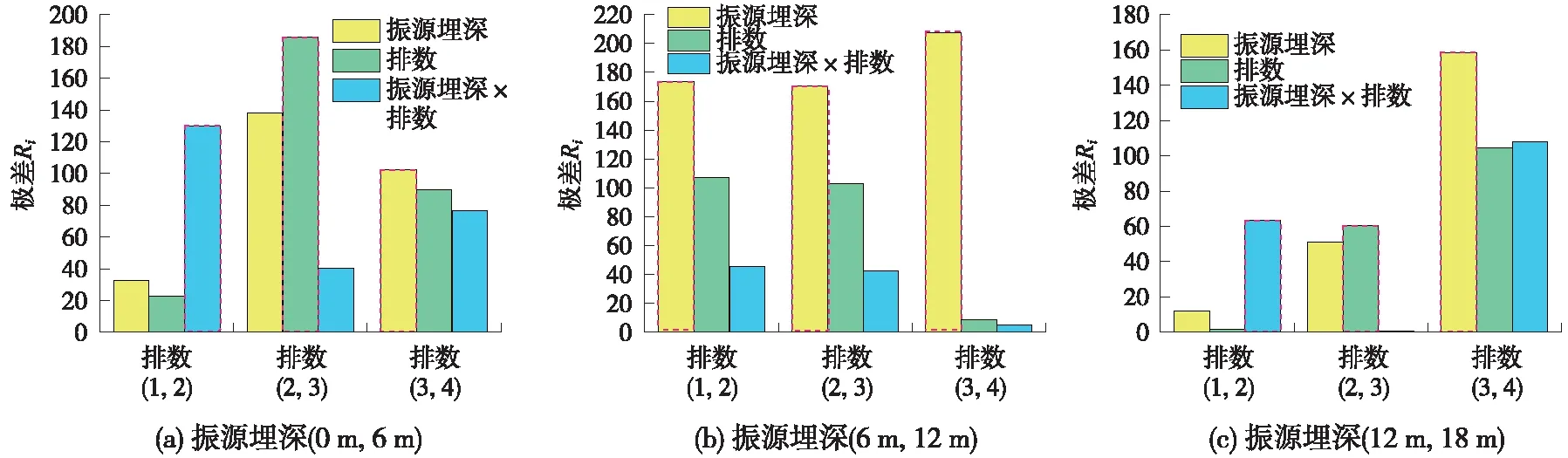
圖10 豎直向振源埋深和排數的交互作用極差

表10 豎直方向隧道埋深-排數交互主導因素

表11 豎直方向樁長-隧道埋深交互主導因素

表12 豎直方向樁長-排數交互主導因素

表13 水平向隧道埋深-排樁到隧道距離交互主導因素

表14 水平向排數-排樁到隧道距離交互主導因素

表15 水平向排數-隧道埋深交互主導因素

分析表8～表15，考察樁排數，為取得較好的豎向衰減效果，排數可以考慮增加到3排，繼續增加排數改善效果不顯著；在距離隧道0.7λSH～2.1λSH區間內布設排樁時，增加排數衰減效果改善明顯；1.4λSH～2.1λSH范圍內增加樁排數到3排就可以獲得較好的水平向衰減，在0.7λSH～1.4λSH范圍內增加到4排效果更佳；當隧道埋深為0.56λSH～1.12λSH時，增加排數，水平向衰減效果改善明顯，4排效果最佳。

考察樁長：隧道埋深不足0.8λSH時，樁長達到3.2λSH即可取得較好的豎向隔振效果；隧道埋深處于1.6λSH～2.4λSH時，在1.6λSH～3.2λSH和4λSH～4.8λSH范圍內增加樁長可有效改善豎直方向隔振效果。

考察排樁到隧道距離：為取得較好的水平向衰減，隧道埋深為0～1.12λSH時，宜采用近場隔振，在距隧道0.7λSH以內設置排樁，效果更顯著；隧道埋深1.12λSH～1.68λSH時，不宜采用近場隔振，在距振源1.4λSH以外布置排樁可取得更好的水平向隔振效果；在近場(0.186λSH～0.7λSH)隔振時增加排樁到隧道距離可改善水平向隔振效果。

3 結論

在粉質黏土地層條件下，針對地下振源、頻段可調的排樁隔振屏障，基于帶隙理論和正交分析理論，研究樁長、排數、列數、隧道埋深以及排樁到隧道距離等因素對振動衰減效果的影響規律，研究結論如下。

(1)各因素對豎向振動衰減影響主次排序：隧道埋深>樁長、排數>列數>排樁到隧道距離。

(2)各因素對水平振動衰減影響主次排序：排樁到隧道距離>隧道埋深、排數>樁長>列數。

(3)為在豎直方向帶隙范圍內取得良好振動衰減效果，建議如下：隧道埋深<0.8λSV時，樁長取3.2λSV；隧道埋深介于1.6λSV～2.4λSV時，在1.6λSV～3.2λSV和4λSV～4.8λSV范圍內增加樁長；排數達到3排就能取得較為穩定的隔振效果。

(4)為在水平方向帶隙范圍內取得良好振動衰減效果，建議如下：距離隧道1.4λSH～2.1λSH范圍內設置排樁，采用3排樁可以取得較為穩定的隔振效果，其他距離建議增至4排；隧道埋深為0～1.12λSH時，距振源0.7λSH以內范圍布置排樁；隧道埋深處于1.12λSH～1.68λSH時，在距隧道1.4λSH以外布置排樁。