運用數學思想，提升學生思維能力
——數形結合思想例談

顧麗鳳

（江蘇省無錫市甘露實驗小學 江蘇無錫 214117）

《義務教育數學課程標準（2011 版）》把“數學的基本思想”作為“四基”目標之一，并明確指出：“數學課程內容不僅包括數學的結果，也包括數學結果的形成過程和蘊涵的數學思想。”數學思想方法是數學知識的靈魂和精髓，是知識轉化為能力的橋梁[1]。掌握數學思想方法，對提升學生的思維品質，對數學學科的后續學習，對其他學科的學習，乃至對學生的終身發展都具有十分重要的意義。那么，在課堂教學中，教師就要有意識地挖掘數學思想方法，讓學生在學習中逐步感悟數學思想，切實提高數學素養。下面就以“數形結合思想”為例，粗淺地談談我在教學時是如何運用數學思想方法，幫助學生提高數學思考能力的。

“數”與“形”是貫穿整個小學數學教材的兩條主線，是貫穿小學數學教學始終的基本內容。我國著名數學家華羅庚先生說過：“數無形，少直觀；形無數，難入微?！睌敌谓Y合思想是小學階段的一種重要數學思想，數形結合，優勢互補，相輔相成，各展其長，有機地使邏輯思維和形象思維統一了起來。因此，教師在教學時，要根據數與形之間的對應關系，把數與形有機地結合在一起，通過數與形的相互轉化，培養學生“見數想形，因形思數，數形結合”的數學意識，引導學生有效解決問題。

一、數形結合，化解學習難點

數形結合不僅是一種數學思想，也是一種很好的數學方法。對于題型結構復雜、抽象，學生難于理解和掌握的教學內容，在教學時，教師可以充分利用“形”的直觀、形象，引導學生有效地運用數學知識、探尋解題的方向和入口，使數學思想方法在知識能力的形成過程中共同生成。

案例：《行程問題》（四下）

出示例題：小明和小芳同時從家出發走向學校。小明每分鐘走70 米，小芳每分鐘走60 米，經過4 分鐘兩人在校門口相遇。他們兩家相距多少米？

師：你能結合圖，說說小明和小芳兩人上學時的情景嗎？

生1：小明和小芳兩人是同時從家出發的。

生2：小明和小芳兩人是面對面地走。

師：兩人面對面地走，這是“相向而行”。

生3：小明和小芳最后在校門口相遇。

師：你能用畫圖的方法來整理題目中的條件和問題嗎？

引導學生根據題意畫出線段圖。

師：現在從圖中你能一眼看出題中的條件和問題了嗎？

你能根據所畫的圖來解決這個問題了嗎？

由于相遇問題是形式化的數學模型，問題的結構比較抽象，且涉及運行時間、方向等諸多因素，學生理解起來有一定的困難。為此，根據題意畫圖整理題中的條件和問題，并借助直觀圖分析數量關系 ，化解了學習的難點，從而能幫助學生順利進行解答。

二、數形結合， 理解數量關系

實際問題中的數量關系是抽象化的，對于一些學生來說，很難理解題中的數量關系，為幫助學生更好地解答實際問題，提高學生的解題能力，教師在教學中可以引導學生通過畫圖，進行“數”與“形”的轉化，把“看不見”變“看得見”，化抽象的數量關系為形象的圖形，從而更好地幫助學生理解數量關系，提升學生的思維能力。

案例：《畫示意圖》（四下）

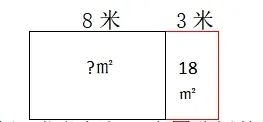
出示例題：梅山小學有一塊長方形花圃，長8 米。在修建校園時，花圃的長增加了3 米，這樣面積就增加了18 平方米。原來花圃的面積是多少平方米？

師：根據題中的條件和問題，你能想到什么？

生1：花圃的長增加了3 米是什么意思？

生2：要求“原來花圃的面積是多少平方米？”，寬未知，怎么求寬呢？

師：想一想，要把題里數量之間的關系看得很清楚，有沒有什么好的辦法？

生：用畫圖的方法，應該可以看得更清楚。

師：那就請同學們試著畫圖吧。

學生在教師的幫助下畫出了示意圖。

師：你能根據示意圖分析數量關系，確定先算什么嗎？

生1：要求原來花圃的面積，要先算它的寬是多少米。

生2：花圃的長增加了3 米，實際上就是增加了一個寬為3米的小長方形。

生3：原來花圃的寬，就是增加的小長方形的長。

生4：面積增加了18 平方米，就是增加的小長方形的面積。

生5：根據18 平方米和3 米，可以求出增加的小長方形的長，也就是原來花圃的寬。

這一教學片斷，通過引導學生畫示意圖，在分析數量關系和解決問題之間架設起了一座橋梁，學生從示意圖中直觀地理解了題意，發現了數量之間的關系，從而使抽象的數學問題具形化，輕松簡單地解決了問題，同時通過這道題的講解，學生切實感受到了畫圖的重要作用，對數形結合思想在解題中的運用起到了潛移默化的作用。

三、數形結合，探索數學規律

學生的學習應當是一個生動活潑的，主動的和富有個性的探索和思考的過程。運用數形結合的思想方法，有助于學生探索數學規律。在教學中，教師要抓住時機，適時引領學生經歷知識的形成過程，學會構造模型來直觀描述數學問題，從中感悟數學思想方法，培養學生思維的創造性，提升學生的數學素養。

案例：《轉化》（五下）

第一步：讓學生仔細觀察給出的算式，引導學生用自己的方式說清楚算式的特點。

第二步：讓學生嘗試用自己的方法計算出結果，并要求他們在小組內交流各自的計算方法。

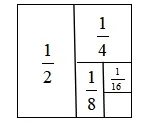
第四步：引導學生將根據圖形想到的計算方法與自己先前采用的計算方法進行對比 ，說說哪一個更簡便。回顧解題過程，反思解題方法，讓學生說說哪個環節對自己的啟發最大。

這一教學過程，在學生觀察算式特點后，啟發他們產生采用非常規思路進行計算的解題需求，教師適時出示“形”，引導學生借助圖形的直觀來解決問題。“形”的出現，豐富了學生的表象，引發了學生更深層次的思考，他們清晰地發現了規律，從而化難為易，把一組連加計算轉化成了簡單的減法計算。在此思考過程中，學生實實在在地感受到了數形結合的思想方法對于數學學習的價值。

四、數形結合，揭示圖形特點

“形”有其直觀形象的優勢，但也有其粗略、不便于表達的劣勢。在教學中，教師要順勢引導學生數形結合，讓學生借助數的優勢來彌補形的不足，使學生在獲得知識的同時，感悟到數學思想方法的價值，使數形結合的思想方法扎根學生心中。

案例：三塊邊長都是12 厘米的正方形鐵皮，分別按下圖剪下不同規格的圓片。剩下的鐵皮面積相等嗎？（五下）

(1)

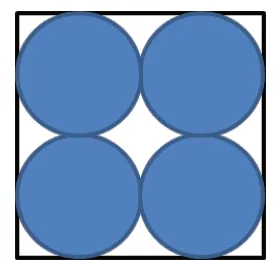
(2)

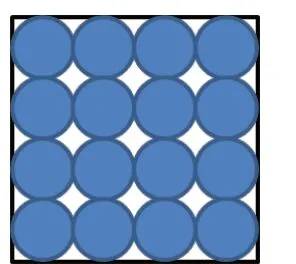
(3)

這是一個圖形的面積問題，但是如果我們只從形的角度直觀觀察是無法得到結果的，即便學生能猜到結果，但也是沒有依據的。因此在教學中必須引導學生從數的角度，通過計算去加以說明驗證。

圖（1）圓的面積：π×（12÷2）2=36π

圖（2）圓面積之和：π×（12÷2÷2）2×4=36π

圖（3）圓面積之和：π×（12÷4÷2）2×16=36π

這樣，通過計算，學生對正方形里圓面積之間的關系有了更加理性和深入的認識，學生也深刻體會到了數形結合思想在解決問題中的有利作用。

數學思想方法是溝通知識與能力的橋梁，在課堂教學中，教師要深入鉆研教材，做教學的有心人，努力挖掘教材中可以進行數學思想方法滲透的各種因素，從學生發展的全局著眼，從具體的教學過程入手，把滲透數學思想方法教學作為一種有意識的教學行為，引導學生在學習過程中不僅僅滿足于正確知識結論的獲得，更應著力于對知識形成過程的理解，領會蘊涵其中的數學思想方法，提高數學素養。