計及分布式電源不確定性的多微網魯棒博弈研究

姜明軍,任明遠,徐蘭蘭,孫旺青,劉曉峰

（1.國網甘肅省電力公司，甘肅 蘭州730046；2.國網甘肅省電力公司 營銷服務中心，甘肅 蘭州730046；3.南京師范大學 電氣與自動化工程學院，江蘇 南京210023；4.東南大學 電氣工程學院，江蘇 南京210096）

0 引言

近年來，我國電力能源行業飛速發展，電網中風、光等分布式電源的接入比例不斷提高，有效緩解了能源緊缺問題。為了提高可再生能源利用效率，通常以微網形式實現可再生能源的就地消納[1]，[2]。微網一般由分布式電源、儲能系統和負荷構成，可以在并網與孤島模式下運行。然而，由于單個微網發展規模較小，供電可靠性低，因此往往將地域相鄰的各微網互聯組成多微網系統[3]，[4]。多微網系統不僅可以降低微網對大電網的依賴，增強供電可靠性，還可以促進分布式電源就地消納，提升微網的經濟效益。

現階段，針對多微網系統調度優化問題的研究主要以系統運行成本最小化為目標構建調度模型，進而利用相關優化算法求解。文獻[5]結合遺傳與模擬退火算法求解微網全壽命周期成本與收益調度模型，可以在維持系統穩定的同時降低運行成本。文獻[6]構建了微網群之間的主從博弈模型，有效提高了多微網的經濟效益。文獻[7]提出一種聯合優化調度模型，上層以調度中心成本最小為目標，下層以各微網成本最小為目標，并設計了基于塊坐標下降-不精確嵌套乘子法的求解算法，可以有效完成多微網的雙層優化。

上述文獻從不同方面開展對多微網系統的調度優化研究，卻忽略了分布式電源出力的不確定性[8]～[10]。目前，已有學者對單個微網的不確定性展開了研究。文獻[11]考慮了微網分布式電源和負荷的不確定性，采用Benders分解算法對所構建的不確定性優化模型進行求解，與改進的非支配排序遺傳算法相比，其魯棒性更優。文獻[12]構建了計及分布式電源不確定性的微網調度魯棒優化模型，并采用多階段求解策略對其求解。文獻[13]提出了一種模糊隨機優化方法，為求解交直流混合微網調度的不確定性問題提供了新思路。文獻[11]～[13]均以單微網為研究對象，均屬于單主體決策的不確定性問題。多微網系統中存在多個微網，各微網分布式電源出力均存在不確定性，對整個多微網系統將產生重要影響。因此，開展多主體決策不確定性問題的研究，對于多微網系統的運行優化調度具有重要意義。

針對多微網系統分布式電源出力的不確定性問題，本文構建了以各微網運行費用最小為目標的非合作魯棒博弈優化模型，從而可以解決計及不確定性的多主體決策問題。本文首先建立了多微網系統分布式電源、儲能系統以及負荷響應模型；然后構建了各微網在非合作方式下的魯棒博弈模型，并給出了求解方法；最后通過算例仿真驗證了所提方法的有效性。

1 系統模型

本文所述場景如圖1所示。多微網系統由N個微網組成，微網由風光分布式電源、儲能系統和用戶負荷構成，微網間可通過信息網絡實現信息的交互。多微網系統控制中心負責用戶負荷、電價等信息的收集與發布。

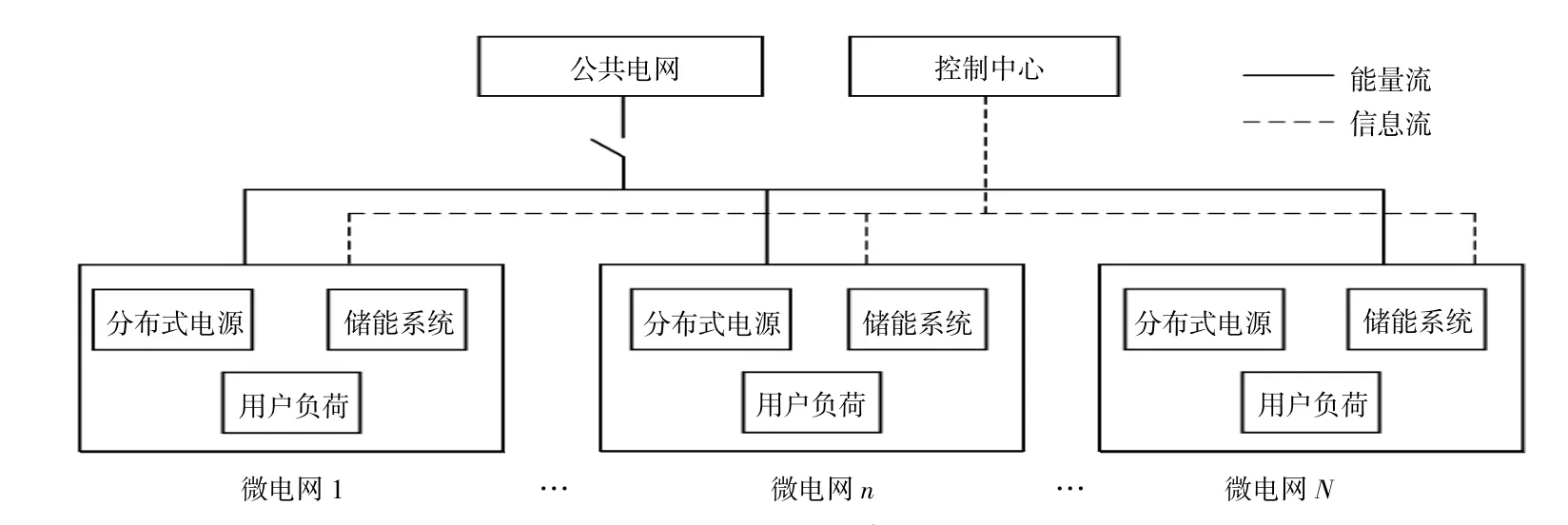
圖1 多微網系統場景Fig.1 Scenario of multi-microgrid system

1.1 分布式電源模型

風光分布式電源既能滿足用戶負荷需求，也能在負荷低谷時段為儲能系統充電，從而可以提升多微網系統的新能源消納率，降低系統運行成本。微網n須要支付分布式電源發電費用，其費用表示為[14]

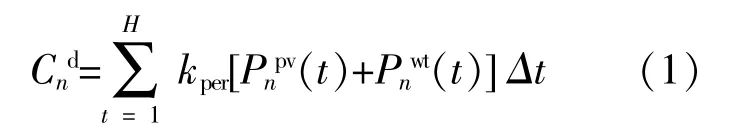
式中：kper為折算后的單位發電成本；Pnpv（t）為t時段微網n的光伏出力；Pnwt（t）為t時段微網n的風電出力；H為調度周期；Δt為各時段間隔。

1.2 儲能系統模型

為了降低微網運行成本，儲能系統在負荷低谷時段存儲分布式電源的過剩電量，在用能高峰時為用戶提供電能。微網須要支付儲能系統日常運維費用，微網n儲能系統在t時段內的費用Cnopt表示為[15]

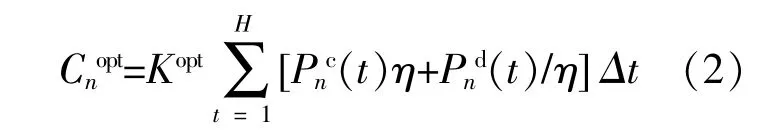
式中：Kopt為儲能系統單位運維成本；Pnc（t）為t時段內的充電功率；Pnd（t）為t時段內放電功率；η為儲能系統的充放電效率。

儲能系統在運行過程中須滿足以下約束：約束（3）表示儲能充放電功率約束；約束（4）表示在一個調度周期的始末時刻剩余電量保持相等；約束（5）表示儲能負荷狀態約束。

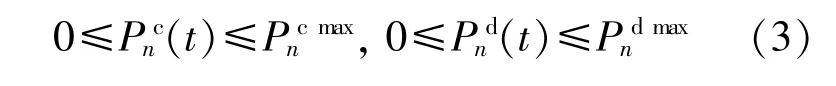
1.3 用戶負荷響應模型

用戶負荷可以通過參與需求響應（DR）來實現資源的優化配置。用戶負荷參與DR本質上不是為了減少負荷消耗，而是將可轉移負荷轉移至低谷時段。因此，用戶負荷響應模型可表示為以下形式：

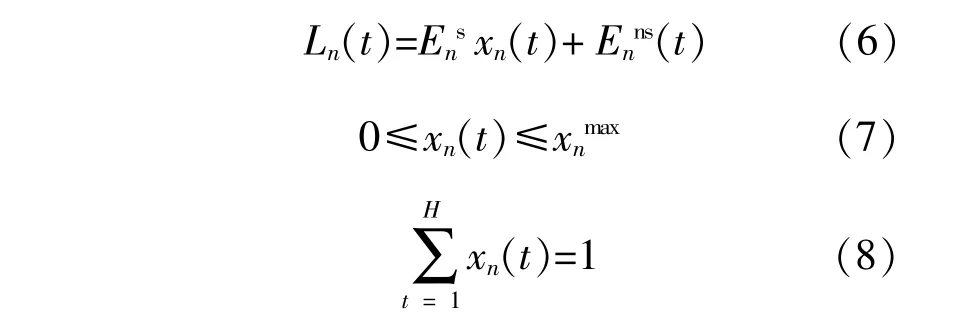
式中；Ln（t）為微網n參與DR后在t時段內的負荷需求；Ens為微網n可轉移負荷總量；Enns（t）為微網n在t時段不可轉移負荷量；xn（t）為微網n可轉移負荷在t時段內轉移比例；xnmax為可轉移比例最大值。

1.4 微網能耗費用模型

在分布式電源無法滿足用戶負荷需求時，微網須要從公共電網購電。假設微網n在t時段內的購電功率為pnbuy（t），則多微網系統在t時段總購電功率為

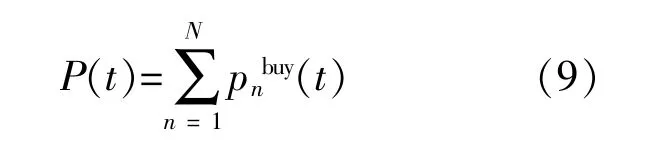
考慮到現階段電網所采用的電價機制多為分時電價、實時電價等，本文假設微網和公共電網之間的市場交易以實時電價進行結算[16]。電價與負荷需求呈正相關，即需求越高，電價就越高。鑒于此，多微網系統在t時段總購電費用為

2 多微網系統魯棒博弈

基于多微網系統中參與個體的趨利性，各微網首先考慮實現自身利益的最大化，因此存在著非合作博弈的競爭行為。非合作博弈不存在利益分配問題，盡管其產生的效益會不及合作博弈，但不會像合作博弈那樣，一旦出現利益分配不均，就會導致合作聯盟瓦解的問題。此外，各微網分布式電源出力均存在不確定性，給微網系統內部的能源調度帶來了較大困難。本文基于魯棒優化和非合作博弈理論，構建了多微網系統非合作魯棒博弈模型，并基于列約束生成算法和強對偶原理，將模型解耦為主問題和子問題進行求解。

2.1 魯棒博弈模型

微網日運行費用主要包括分布電源、儲能系統的運維費用和向電網購電的費用；運行收益為反向售電收益。微網n日支出成本為

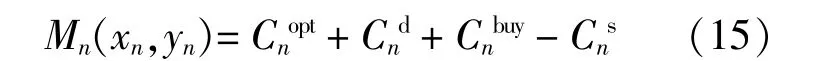
式中：xn為微網n日前DR負荷調度的決策向量，xn=[xn（1），xn（2），…，xn（H）]；yn為微網n的購電、售電、充電、放電的決策量，yn=[Pnbuy，Pns，Pnc，Pnd]。

在不考慮分布式電源出力不確定性時，上述多微網經濟調度問題的確定性優化模型如式（16）所示。約束條件第1行對應優化模型中的不等式約束（3），（5），（7）；約束條件第2行對應優化模型中的等式約束（4），（8）；約束條件第3行對應優化模型中的功率約束（14）。

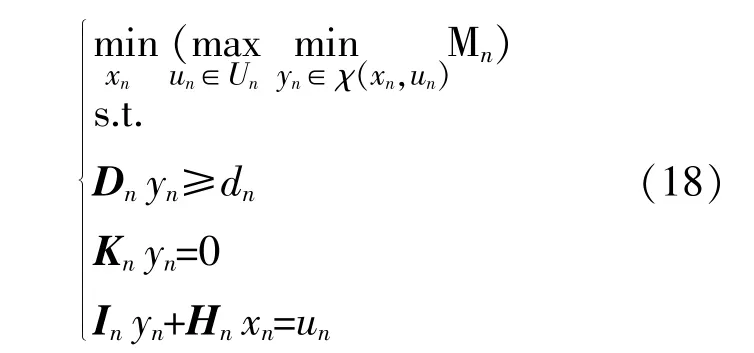
式中：χ（xn，un）為給定xn和un之后yn的可行域。

基于模型式（18），多微網系統非合作魯棒博弈模型可建立以下形式：①參與者：所有微網用戶；②策略集：各微網用戶調度策略xn和yn；③收益函數：微網n參與博弈的收益Pn。

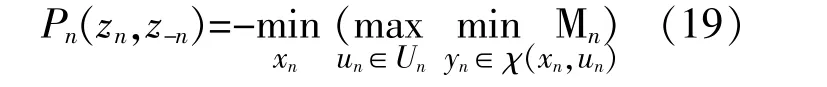
式中：zn為微網n的調度策略，zn=[xn，yn]；z-n為其他所有微網調度策略，z-n=[x-n，y-n]。

微網參與上述博弈的目標為實現自身利益最大化，當多微網系統中所有微網收益均達到最大，即博弈達到了均衡狀態。該均衡狀態稱為Nash均衡：

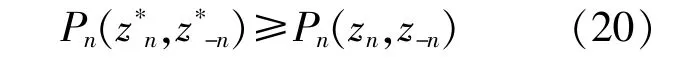
式中：（z*n，z*-n）為所構建非合作博弈模型的Nash均衡點。

2.2 模型轉化

為求解非合作博弈模型Nash均衡解，須要對模型（19）進行轉化。當微網n在求解自身最優策略z*n時，其余微網策略集z*-n可視為已知的常量。因此，對模型（19）的轉化實際上就是對式（18）進行轉化。因此，本文采用列約束生成算法，將模型（18）分解為主問題和子問題進行交替求解，進而得到原問題的最優解。根據列約束生成算法，式（18）分解后的主問題為

式中：M為足夠大正數；Δun為微網n分布式電源出力預測誤差向量；zn1和zn2為引入的連續輔助變量。

2.3 算法流程

經上述推導和轉換，魯棒博弈模型最終解耦為具有混合整數線性形式的主問題（21）和子問題（25），魯棒博弈模型的求解算法如下。

將非合作魯棒博弈模型（19）分解為主問題和子問題，并給定各微網初始場景u1，u2，…，un。設置調度方案成本上界UB=+∞，下界LB=-∞，迭代次數k=1，收斂閾值ε=10-3，多微網非合作博弈均衡解求解過程：

①初始化各微網策略zn與z-n；

②微網n根據當前場景un和其他微網策略集z-n求解問題（21），得到最優策略；

③根據微網n的最優策略，依次更新其他微網策略得到新的策略集z-n；

④返回步驟①，直至所有微網策略不再改變；

⑤根據微網總支出函數更新下界LB。

令k=k+1，返回步驟①。

3 仿真結果

為了驗證本文所構建的多微網系統非合作魯棒博弈優化模型的有效性，以N=3微網構成的多微網系統為例，求解出計及分布式電源出力不確定性的微網魯棒調度計劃及均衡解。

算例仿真主要參數設置如下。將1 d分為24個時段（H=24），各時段間隔Δt=1 h。根據負荷水平將1 d分為3個時段，即低谷時段（0：00-6：00和22：00-24：00）、平時段（6：00-17：00）和高峰時段（17：00-22：00）。低谷時段的a（t），b（t）分別為0.2和53；平時段的a（t），b（t）分別為0.3和111；高峰時段的a（t），b（t）分別為0.4和179。微網反向售電價格ks=37美元/（MW·h），儲能系統運維成本Kopt=1.35美元/（MW·h）。最大充電功率限制Pcmax=0.7MW·h，最大放電功率限制Pdmax=1MW·h，儲能系統充、放電效率均為92%。考慮到多微網系統在地理位置上相距較近，風光等資源條件近似，本算例假設各微網配置了相同容量的儲能系統，而且分布式電源的出力相同。各微網負荷需求和分布式電源預測值和實際值如圖2所示。

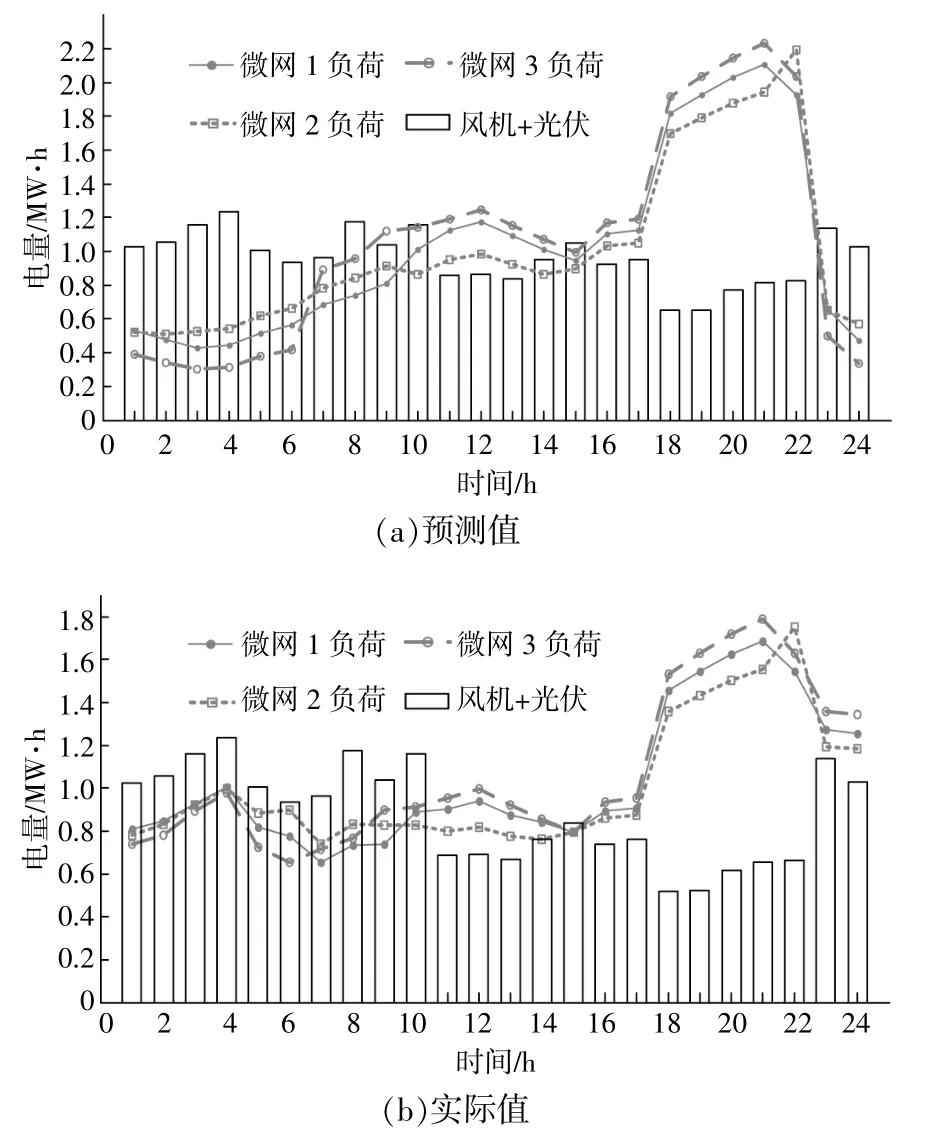
圖2 微網負荷及分布式電源預測值和實際值Fig.2 Load distribution and predicted and actual values of distributed energy

3.1 多微網系統調度方案

基于以上參數，可以得到多微網系統優化調度方案。圖3所示為多微網系統參與非合作博弈后的魯棒調度優化結果。圖中所示結果為微網可轉移負荷占總負荷20%情況下的調度結果。從圖3中可以看出，各微網主要在低谷時 段（0：00-6：00，22：00-24：00）從公共電網購電，從而降低購能費用；微網在低谷時段內未出現大量集中購電的行為，購電時間分布較為均勻，未對電網造成沖擊；儲能系統的充電行為主要集中在低谷時段，并在高峰時段（17：00-22：00）為微網負荷提供電能，可以進一步降低微網日運行費用。

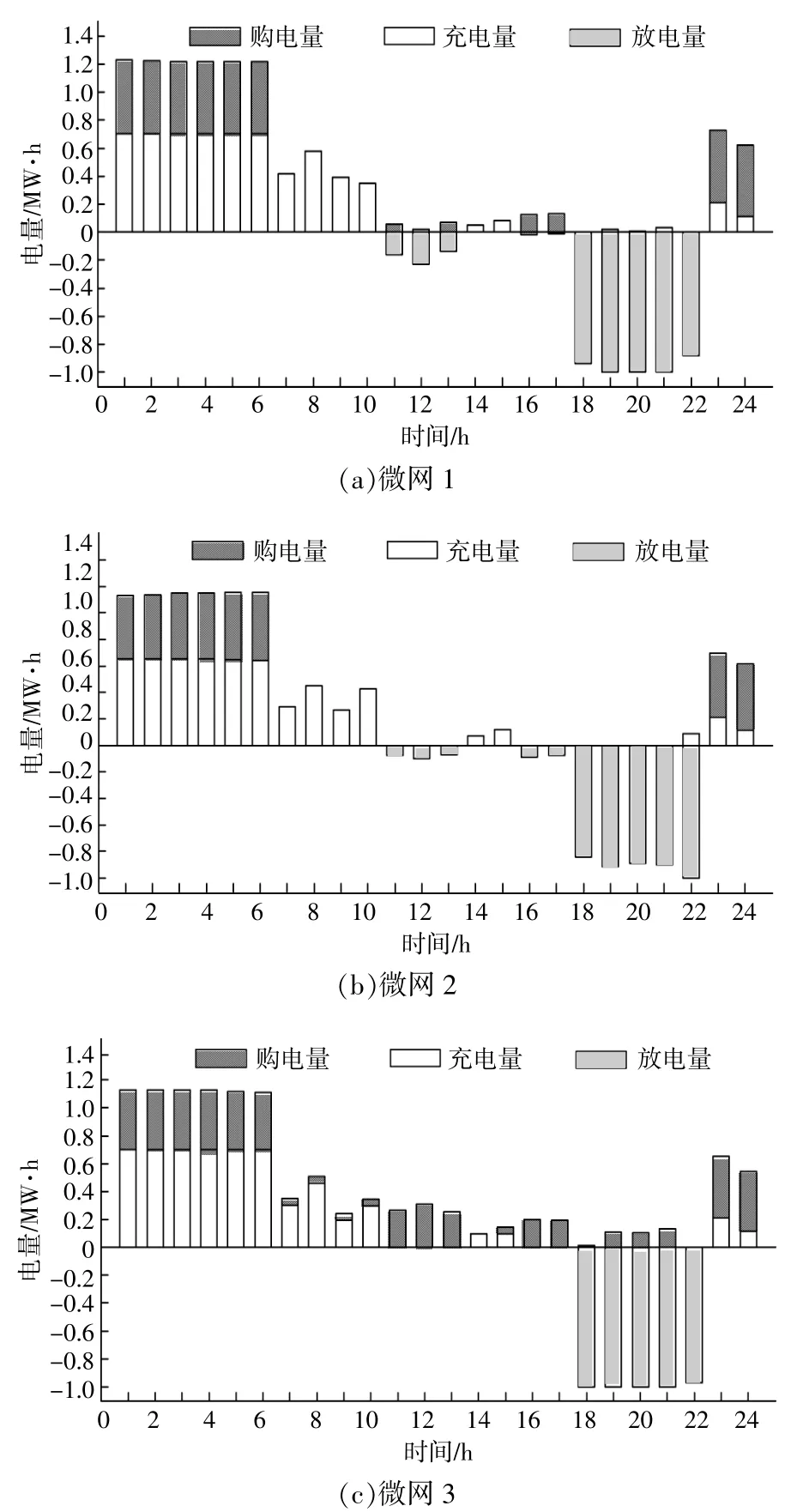
圖3 非合作博弈魯棒調度結果Fig.3 Robust scheduling results of non-cooperative game

微網可轉移負荷占總負荷比重的大小對調度結果會產生較大影響。表1所示為多微網系統中可轉移負荷占比分別為0%，20%，30%和40%時的調度結果分析。從表1可以看出，隨著可轉移負荷比例的增加，微網從公共電網的購電量呈現逐步下降的趨勢，儲能系統的充、放電量下降趨勢較為明顯。這主要是由于微網系統負荷總量沒有改變，只是通過DR將負荷進行了轉移。隨著負荷不斷從高峰時段轉移至低谷時段，這些可轉移負荷需求可直接由分布式電源來供應，所以無須儲能系統頻繁地參與調度，同時也減少向電網購電的電量。因此，隨著可轉移負荷占比的提升，多微網系統總費用也會逐步降低。

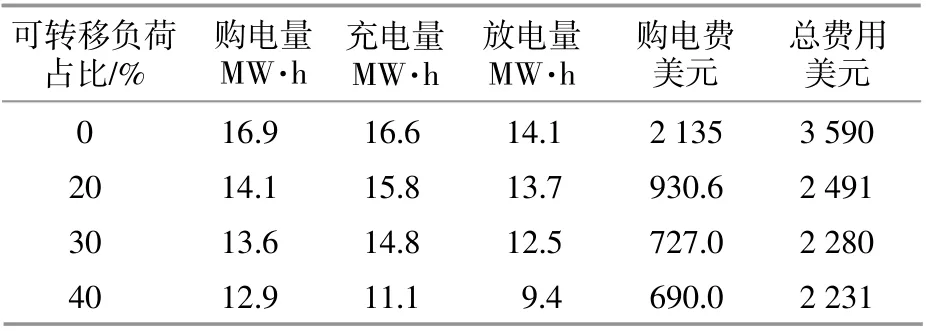
表1 可轉移負荷對優化結果影響Table 1 The effects of shiftable loads on optimization result

表2分別給出了多微網系統參與優化前和參與魯棒博弈時的費用對比（可轉移負荷量均為20%）。從表2中可以看出，在微網參與調度優化后，從電網購電的費用下降了56.4%，總體費用下降了30.6%。多微網系統參與魯棒博弈優化后，可以顯著提高系統的運行經濟性。

表2 多微網系統優化前后費用對比Table 2 Multi-microgrid's cost before and after optimization

3.2 優化模型對比

為了驗證本文所提出的魯棒博弈優化模型的有效性以及調度方案的保守性，對常規確定性模型和非合作魯棒博弈模型進行了比較。

圖4為微網2儲能系統在兩種調度模式下的調度安排。

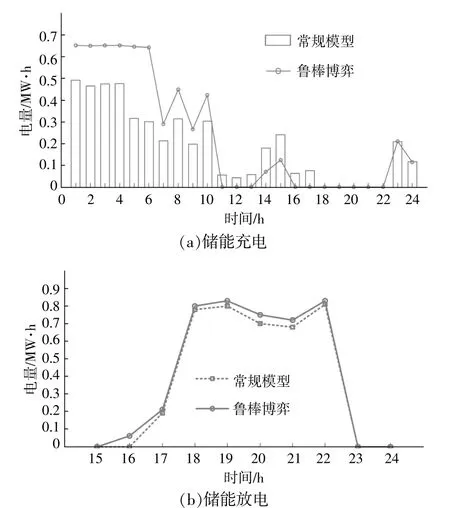
圖4 兩種調度方式儲能充放電對比Fig.4 Charging/discharging comparison of energy storage under two dispatch strategies

由圖4（a）可見，常規確定性模型中的儲能在平時段的充電量要高于魯棒博弈調度，在低谷時段的充電量要少于魯棒博弈調度。這是因為魯棒博弈得到的優化結果考慮了不確定因素，減少了在平時段的購電量，增加了在電價較低的低谷時段的充電量，降低了調度風險。

由圖4（b）可見，為了應對分布式電源出力的不確定性，通過魯棒博弈調度提高了儲能調度的積極性，使其高于確定性調度模式，利用儲能來降低分布式電源出力波動對系統的影響。魯棒博弈總計放電量達到了4.7 MW·h，比確定性調度博弈（3.9 MW·h）增加了20.5%。

圖5為不同保守度情況下的各微網儲能充電策略對比。其中，場景1調節參數Γn=8，分布式電源出力最大波動為10%；場景2調節參數Γn=15，出力最大波動為10%；場景3調節參數Γn=15，出力最大波動為20%。從調度結果可以看出，當魯棒調節參數Γn增加時或者分布式電源波動變劇烈時，儲能會降低平峰時段的充電量，進而選擇在低谷時段進行充電。這種更保守的行為可以避免在平時段因分布式電源出力不足而帶來的能源短缺風險。

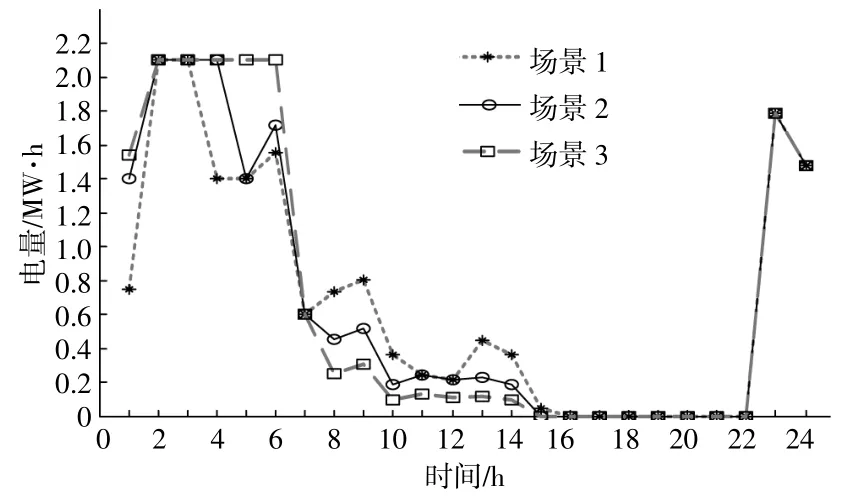
圖5 3種場景下微網儲能的魯棒充電策略Fig.5 Charging strategy of energy storage under three different cases

為了驗證本文所提出的調度方案的經濟性，在分布式電源出力歷史數據基礎上，隨機模擬了45組不同出力數據，來比較兩種調度模式在應對分布式電源出力波動時的經濟性。圖6（a）、圖6（b）、圖6（c）分別對應Γn=5，Γn=10和Γn=15情況下的費用（分布式電源出力最大波動均為20%）。當預測精度較高時，即如圖6（a）中的15組場景所示，確定性調度方案有更好的經濟性。隨著預測精度的下降，如圖6（b）、圖6（c）所示，魯棒博弈的經濟性要明顯強于確定性調度方案。因此，決策者可以根據分布式電源出力預測精度來調節不確定性參數Γn，從而可以保證調度方案在具備經濟性的同時，又具備一定的魯棒性。

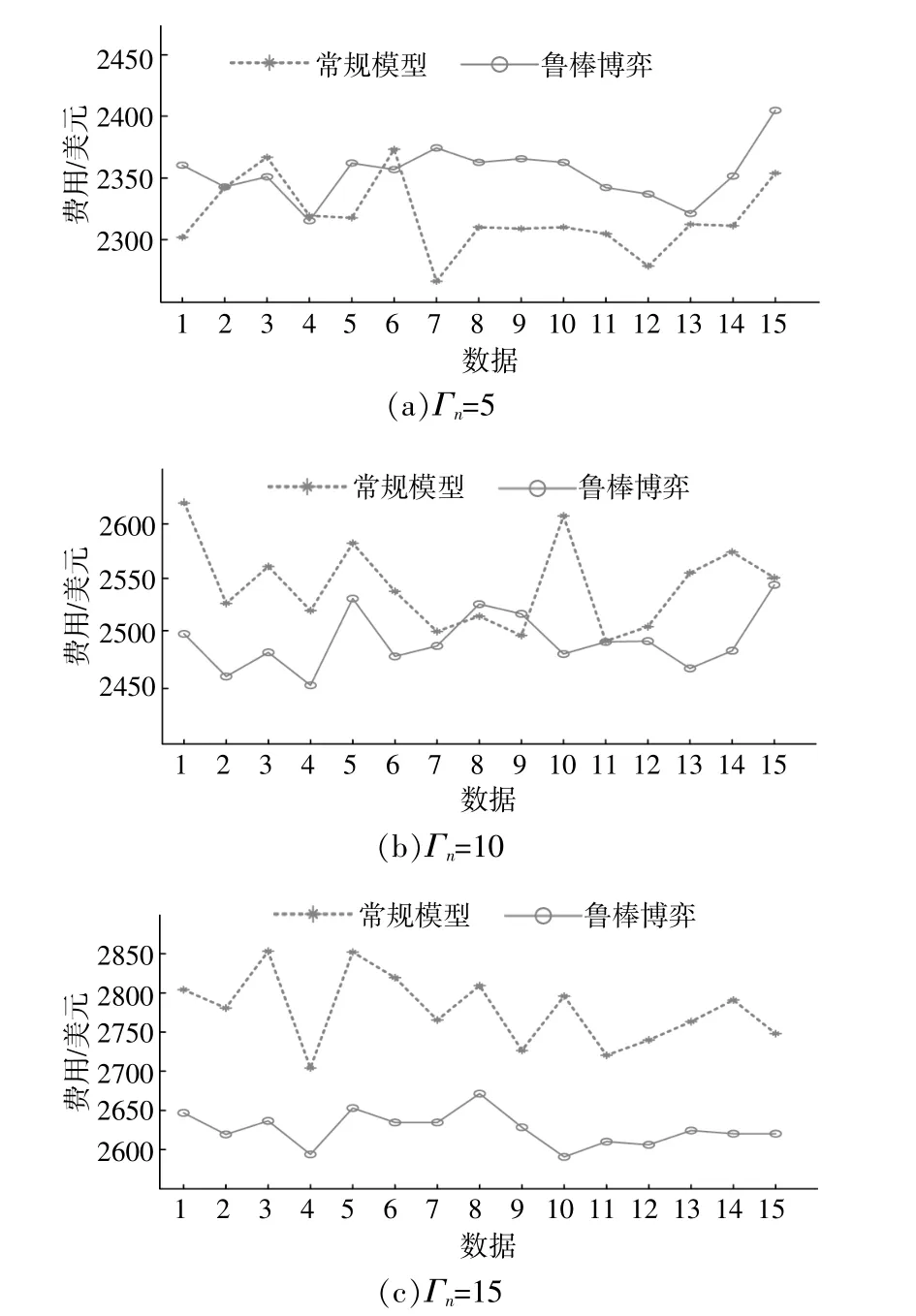
圖6 不同出力下兩種調度方式的經濟性對比Fig.6 Economic comparison of two dispatch strategies for different energy output

4 結論

針對多微網系統分布式電源出力的不確定性問題，基于魯棒優化和博弈理論構建了多微網系統非合作魯棒博弈優化模型。

本文所提出的模型考慮了分布式電源的不確定性，通過對多微網魯棒博弈模型的求解，可以得到各微網在非合作博弈模式下的魯棒調度方案。

為了解決魯棒優化過于保守的問題，所構建的模型中引入了不確定性調節參數，可以根據分布式電源出力預測精度來調節調度方案的保守性。

在分布式電源出力預測精度較高情況下，魯棒博弈調度方案的經濟性不及確定性調度方案；但隨著預測誤差的增大，魯棒博弈調度方案的經濟性逐漸優于確定性調度方案。