基于MIMO雷達的極化平滑降維酉ESPRIT算法

陳 晨 陶建鋒 鄭桂妹

(1. 空軍工程大學研究生學院, 陜西西安 710051; 2. 空軍工程大學防空反導學院, 陜西西安 710051)

1 引 言

MIMO雷達[1-2]本質上是將通信領域中的多輸入多輸出技術應用到雷達領域,進而和數字陣列雷達技術進行優勢互補所形成的一種新型雷達。MIMO雷達由于采用了波形分集技術,和傳統相控陣雷達相比,其具有抗干擾能力強、分辨率高、多目標跟蹤能力強的優點,這引起了國內外研究人員的高度關注。根據收發陣元的距離,MIMO雷達可以分為兩大類:集中式MIMO雷達和分布式MIMO雷達。集中式MIMO雷達收發天線各單元相距較近,主要利用波形分集和多通道相干性,進而擴展陣列虛擬孔徑,提高角度分辨率和抗干擾能力。分布式MIMO雷達收發天線距離較遠,每對收發天線均可以當作一組雙基地雷達,利用目標回波的空間分集增益,可以提高角閃爍目標的檢測性能。

本文主要研究集中式單基地MIMO雷達的波達方向(Direction-Of-Arrival, DOA)估計問題,這是雷達信號處理領域的重點與難點,廣受國內外學者的關注。由于MIMO雷達具有常規陣列雷達所沒有的優勢(抗干擾能力強、分辨率高、多目標跟蹤能力強),所以眾多研究人員開始關注并研究MIMO雷達的DOA估計方法,在MIMO雷達的基礎上提出了許多新的、更有效的DOA估計方法[3-15]。文獻[3]提出了一種譜值優選算法,該算法抑制了目標閃爍且提高了DOA估計精度。文獻[4-5]將ESPRIT算法應用到了MIMO雷達系統中,該方法可以有效地估計出信號的波達角,且運算量較小。文獻[6]將MUSIC算法應用到MIMO雷達中,在一定程度上降低了算法復雜度且獲得了不錯的DOA估計精度,但是MUSIC算法需要進行譜峰搜索,因此該算法計算量仍然較高。針對該問題,文獻[7]提出了一種基于MIMO雷達低復雜度的求根MUSIC算法,其計算量顯著下降,但是DOA估計精度也隨之下降。此外可以發現上述算法均假設目標是不相干的,但是在實際應用中存在大量相干目標,而最大似然估計算法可以有效的解決相干信源問題。因此文獻[8-9]將最大似然估計算法應用到MIMO雷達上面,解決了相干信源問題,但最大似然估計算法需要參數搜索,算法復雜度較高,不利于現實應用。文獻[10-11]將雙向空間平滑算法與MIMO雷達相結合,取得了不錯的解相干能力,但其解相干能力是以犧牲陣元數目為代價獲得,陣列孔徑有一定的損失。極化平滑算法具有解相干的能力,且不損失陣列孔徑,因此文獻[12]提出了一種基于MIMO雷達的極化平滑廣義MUSIC算法,解決了低仰角多徑相干問題,且精度較高,這表明了極化平滑算法在MIMO雷達中可以獲得好的解相干能力。MIMO雷達具有波束數目較多、波束駐留時間長等特點,因此利用MIMO雷達進行DOA估計,其計算量天然的大于普通陣列雷達。針對這個問題文獻[13]提出了一種降維ESPRIT算法,該算法降低了MIMO雷達導向矢量維度,進而使得MIMO雷達復雜度變低,但是該算法完全在復數域進行,沒有充分利用共軛接收數據,角度估計精度有待提高。文獻[14]將酉ESPRIT算法[15]應用于MIMO雷達DOA估計中,該算法利用酉矩陣對接收數據進行實值處理使其變為實數數據,且利用了共軛接收數據。

文獻[16]提出了一種降維酉ESPRIT算法,該算法即降低了運算復雜度又有較高的測角精度,但該算法沒有考慮相干信號源。此外,文獻[13-14]中的算法均不能估計相干信源仰角,不夠貼合實際。本文為了與實際需求貼合,在達到好的解相干能力的同時降低運算量,提出了一種基于極化平滑的降維酉ESPRIT算法:首先利用降維變換矩陣將接收信號數據由高維矩陣變為低維矩陣,然后利用降維后的接收信號數據構造出一個中心復共軛對稱矩陣,對降維后的接收信號矩陣進行實值處理,接下來對其進行極化平滑解相干處理,最后構造出旋轉不變關系式實現DOA估計。此外酉ESPRIT算法可以使數據樣本加倍[14],因此本文算法可以獲得更好的DOA估計精度。

2 信號模型

(1)

gp為第p個目標的極化導向矢量[17]:

(2)

式中l=1,...,L;?為Kron積;sp(p=1,...,P)為空間入射的P個相干窄帶信號,其值為復常數,表達式為sp=αps1,p=1,...,P,αp=|αp|ejξp其幅值與相位分別代表第p個信號相對于第一個信號的幅度衰落與相位差;βp為第p個目標的復反射系數。θp表示第p個目標的波達角;Nl為匹配濾波后的高斯白噪聲。

式中0≤γp<π/2和-π≤ηk<π為信號極化參數,令G=[g1,...,gP],其為極化導向矢量;φp為方位角,本文只考慮測俯仰角,所以在本文中將其視為先驗信息并設其值φp=90°。發射陣列的第p個目標的空間導向矢量為:

at(θp)=[at1(θp),at2(θp),...,atM(θp)]T=
[1,e-j2πdtsin θp/λ,...,e-j2π(M-1)dtsin θp/λ]T

(3)

接收陣列的第p個目標空間導向矢量為:

ar(θp)=[ar1(θp),ar2(θp),...,arN(θp)]T=
[1,e-j2πdrsin θp/λ,...,e-j2π(N-1)drsin θp/λ]T

(4)

令

A(θ,γ,η)=[g1?ar(θ1)?at(θ1),...,gP?ar(θP)?at(θP)]

(5)

則式(1)可以簡化為:

yl=A(θ,γ,η)cl+Nl

(6)

式(6)中cl=[β1s1,β2s2,...,βPsP]T。收集L個快拍的yl數據,形成矩陣Y,記為:

Y=AC+N(t)

(7)

3 極化平滑降維酉ESPRIT算法

3.1 降維處理

接收陣元由K=6個分量構成,現在考慮相同極化類型的分量的輸出為:

Y(k)=BG(k)C+N(k)(t)

(8)

G(k)=diag(g1(k),...gP(k))為極化導向矢量G的第k個分量,B=ar(θ)?at(θ);Y(k)表示MN維的接收信號矢量,把接收極化敏感陣列分解為K個子陣。

對聯合導向矢量B=ar(θ)?at(θ)進行觀察后可以發現,此導向矢量實際上是由Ne=M+N-1[12]個不同的元素線性組合而成:

B=ar(θ)?at(θ)=Td(θ)

(9)

d(θ)=[1,e-j2πdtsin θp/λ,...,e-j2π(Ne-1)dtsin θp/λ]T

(10)

d(θ)表示Ne×1維的虛擬均勻線陣導向矢量,變換矩陣T[12]為:

(11)

根據式(9)可以將聯合導向矢量矩陣表示為:

B=TD

(12)

上式中D=[d(θ1),...,d(θP)]表示虛擬均勻線陣導向矢量矩陣,將式(12)代入式(8)中可得:

Y(k)=TDG(k)C+N(k)(t)

(13)

從上式可以看出,接收極化信號分量是由虛擬均勻線陣導向矢量D張成的高維空間,因此可以將其轉換到低維空間,降低其維度。設降維變換矩陣為Ne×MN維的矩陣Q,則式(13)經過降維變換后為:

YRD(k)=QTDG(k)C+NRD(k)(t)

(14)

其中NRD(k)(t)=QN(k)(t),降維后的噪聲矢量需為高斯白噪聲,也即降維處理后的噪聲協方差矩陣需為σ2INe,因此不難發現降維矩陣需滿足該式:QQH=INe,我們可以選降維矩陣[12]為

Q=(THT)-1/2TH

(15)

將式(15)代入式(14)可得降維后的協方差矩陣為:

YRD(k)=(THT)-1/2THTDG(k)C+NRD(k)(t)=
(THT)1/2DG(k)C+NRD(k)(t)

(16)

YRD(k)=W1/2DG(k)C+NRD(k)(t)

(17)

由式(17)發現接收極化信號分量經過降維處理后維度變小,且降維矩陣是稀疏的,增加計算量很小。但如果直接構造旋轉不變性方程進行DOA估計,就不能充分利用共軛的觀測數據。因此可以利用酉矩陣對接收數據進行實值處理來提高算法精度,此外通過實值處理還可以進一步降低算法計算量。

3.2 實值極化平滑算法

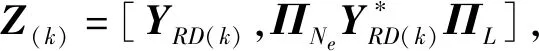
(18)

式中,ΓK[14]為稀疏的酉矩陣,其奇數與偶數維分別定義為:

(19)

經過降維實值處理后的相同極化類型分量數據為V(k),這樣可以求得各個子陣的協方差矩陣為:

(20)

然后對其進行極化平滑處理,極化平滑算法[13]的本質就是對各子陣的協方差矩陣進行均勻加權求和,以恢復數據協方差的秩為滿秩達到解相干的目的。下面證明降維實值后的數據經過極化平滑后的數據協方差仍然為滿秩。極化平滑后的相關矩陣為:

(21)

式(21)中ΓNe為酉矩陣,因此有rank(R)=rank(RZ),RZ可以化簡為下式:

(22)

式(22)中,ΠNe為K×K維的交換矩陣,因此不難得到rank(RZ)=rank(RY),RY繼續化簡可以得出下式:

(23)

式(23)中

(24)

設fk=G(k)C,則有式(24)可寫為下式:

(25)

其中

(26)

此時當P≤K時有rank(R)=rank(RZ)=rank(RY)=rank(RK)=rank(F)=P,由此可見經過降維實值處理后再次進行極化平滑處理后可以恢復數據協方差的秩為滿秩,達到解相干的效果。由理論推導和實驗驗證可知六維極化平滑最多可以估計六個相干信號。

3.3 ESPRIT算法

對式(21)進行特征值分解

(27)

式中,US為大特征值對應的特征矢量張成的實值子空間,也即信號實值子空間。

降維后的數據和均勻線陣接收的數據是等效的,所以可得到降維后復數域的旋轉不變關系式:

J2d(θp)=ejπsin θpJ1d(θp)
J1=[INe-1,0(Ne-1)×1]
J2=[0(Ne-1)×1,INe-1]

(28)

J1,J2可分別選擇d(θp)的前Ne-1行和后Ne-1行。且J2和J1滿足中心對稱關系

J2=ΠNe-1J1ΠNe

(29)

通過均勻線陣的中心對稱關系可以將式(28)變換為實值的旋轉不變關系式[15]

(30)

因此式(30)的實值旋轉不變關系可以寫成矩陣形式:

K2H=K1HΦ

(31)

K2US=K1USψ

(32)

其中ψ=Ω-1ΦΩ,通過最小二乘或者總體最小二乘估計法求解實值矩陣Ψ,對Ψ進行實值特征值分解可以得到最終的波達角估計值。假設Ψ的第p個特征值為λp,則第p個目標的波達角可以由下式估計出:

(33)

4 計算復雜度分析

在算法實現過程中,相比于乘法運算耗費時間來說,加法運算耗費時間可忽略不計,因此本節在進行復雜度分析時,忽略掉加法運算。由文獻[18]可知實數乘法計算量為復數乘法的1/4。本文算法計算復雜度主要分為三個部分:(1)降維處理;(2)實值處理;(3)特征值計算(4)特征值分解,其計算復雜度分別為:

極化ESPRIT算法計算復雜度主要分為兩個部分:(1)特征值計算，(2)特征值分解,其計算量分別為:1)O(6LM4),2)M6/3,則極化ESPRIT算法復雜度為O(6LM4+M6/3)。本文在第5節對兩種算法的復雜度進行了仿真,且進行了詳細的分析。

5 仿真分析

本節主要通過幾組仿真實驗來驗證本文算法的有效性與真實性。為了描述方便,將本文所提算法簡稱為P-RD-UESPRIT,將極化平滑算法簡稱為P-ESPRIT算法。

假設一個均勻線陣組成的全極化MIMO雷達。其發射陣元數和接收陣元數分別為M=8,N=6,工作頻率f=3×108Hz,則波長λ=1 m,且收發陣元間距均為λ/2。假設有6個窄帶相干目標信號,其波達角分別為:θ1=10°,θ2=20°,θ3=30°,θ4=40°,θ5=50°,θ6=60°。定義均方根誤差(Root mean square error,RMSE)來衡量算法的估計性能:

(34)

圖1為本文算法極化處理后信號數據協方差特征值和未經過極化處理的數據協方差特征值點圖,入射信號為六個相干窄帶信號。從圖1中可以看出極化處理前因為相干源的存在,使得協方差秩虧,只存在一個大特征值,而經過極化處理后,數據協方差的秩得到了恢復,存在六個大特征值,與六個相干信號源對應,達到了解相干的目的。

圖1 特征值點圖Fig.1 Eigenvalue dot plot

圖2為本文所提P-RD-UESPRIT算法的波達角估計結果,蒙特卡洛試驗次數K=1000,六個相干目標的信噪比均為10 dB,快拍數snap=100。由圖2可以看出本文所提算法可以正確的估計出6個相干信源的波達角。

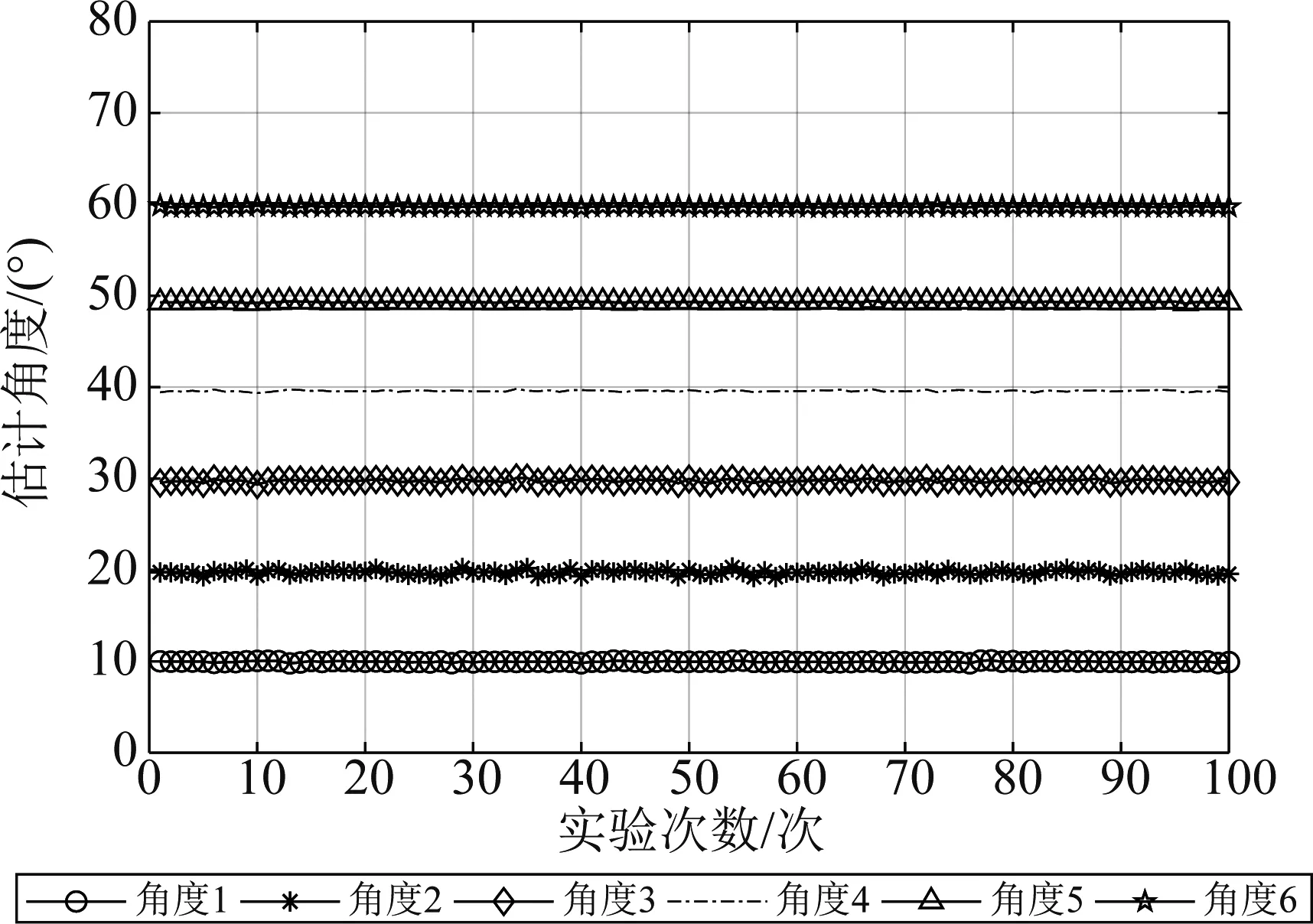
圖2 六個相干目標DOA估計結果Fig.2 DOA estimation results of six coherent targets

圖3為本文所提P-RD-UESPRIT算法和P-ESPRIT算法估計角度RMSE隨目標信噪比變化關系(6個相干目標的信噪比相等),其中快拍數snap=100,蒙特卡洛次數K=1000。從圖中可以看到本文所提P-RD-UESPRIT算法和P-ESPRIT算法估計精度都隨著信噪比增大而改善,且本文所提P-RD-UESPRIT算法精度明顯高于P-ESPRIT算法,這是由于本文所提P-RD-UESPRIT算法在實值處理時數據加倍。

圖3 DOA估計精度信噪比變化關系Fig.3 DOA estimation accuracy signal-to-noise ratio variation

圖4 DOA估計精度隨快拍數變化關系Fig.4 Angle accuracy changes with the number of snapshots

圖4給出了本文所提P-RD-UESPRIT算法和P-ESPRIT算法角度估計RMSE隨快拍數的變化關系圖,六個相干目標的信噪比均為10 dB,蒙特卡洛試驗次數K=1000。從圖中可以看出本文提出的P-RD-UESPRIT算法與P-ESPRIT算法相比,整體精度較高,在低快拍數的情況下P-RD-UESPRIT算法優勢更為明顯。

圖5為本文所提P-RD-UESPRIT算法和P-ESPRIT算法的計算復雜度隨陣元數目變化圖,設置收發天線數目相等,即M=N,快拍數snap=100,目標個數P=6。從圖5中可以看出與P-ESPRIT相比,P-RD-UESPRIT計算復雜度明顯更低,且隨著陣元數目的增大,P-RD-UESPRIT的計算復雜度相比P-ESPRIT將有更大的優勢。

圖5 復雜度隨陣元數目變化關系Fig.5 The relationship between complexity and the number of array elements

6 結論

本文所提的基于極化平滑降維酉ESPRIT算法在一定程度上解決了單基地MIMO雷達相干信號DOA估計問題。該算法通過降維變換矩陣將信號接收數據由高維矩陣降為低維矩陣,然后在低維空間基礎上構造中心復共軛對稱矩陣,再構造出合適的酉矩陣對其進行實值處理,接著對其進行極化平滑處理以達到解相干目的,最后在解相干后的低維實值數據空間構造實值旋轉不變關系式估計出信號的DOA。在理論推導部分證明了降維實值后的數據仍然可以使用極化平滑算法達到解相干的目的,且在第4節對算法復雜度進行了分析。在第5節進行了仿真實現,實驗結果證明了本文算法的正確性,與常規極化平滑ESPRIT算法相比,具有更好的解相干能力、更低的運算量,且在低信噪比、低快拍數時仍然具有不錯的估計精度。