月球基地車輛自校準導航定位方法
崔 軼, 傅惠民
(北京航空航天大學 小樣本技術研究中心, 北京 100191)
0 引言
構建月球基地是月球探測的核心目標之一, 也是人類實現對月球資源的深度開發和利用的重要手段[1,2]。 在月球基地中, 可以通過機器人和智能車輛來控制和照料基地。 因此,為機器人和智能車輛提供導航服務就非常重要。 這種月球基地的導航與一般的月面導航不完全一樣,前者是小范圍的,后者是大范圍的,前者對導航精度的要求遠高于后者, 這導致月球基地機器人和車輛的導航面臨更大的挑戰。 為此,文獻[3]提出一種新的步長估計模型和行人航位自校準推算方法, 并建立一種室內自校準導航定位方法,不但解決了室內行人導航定位問題,而且能夠為月球基地機器人提供高精度的導航定位。 在此基礎上, 本文進一步提出一種月球基地車輛自校準導航定位方法,可以實現月球基地車輛高精度導航定位。
1 慣性導航自校準方程
由于慣性導航系統每次使用之前需要較長的初始對準時間,加上受環境的影響和設備老化等原因,其陀螺儀和加速度計往往存在較大漂移。因此,下面根據慣性導航方程, 給出能夠對陀螺儀和加速度計漂移進行有效修正的自校準方程。
1.1 自校準狀態方程
由于慣性傳感器的采樣頻率非常高, 相鄰兩次采樣之間加速度變化不大,因此其狀態方程可以表示為:

式中:ax,k,ay,k,az,k為第k 次采樣時導航坐標系下車輛質心的三軸加速度,bax,k-1,bay,k-1,baz,k-1為未知輸入 (模型誤差、環境干擾等),wax,k-1,way,k-1,waz,k-1為噪聲。
由運動學方程可知, 車輛行進過程中的位置和速度由下面四式給出:

式中:(xk,yk) 為第k 次采樣時導航坐標系下車輛質心的位 置 坐 標,vx,k,vy,k為 第k 次 采 樣 時 導 航 坐 標 系 下 車 輛 質心的速度, △tk-1為相鄰兩次采樣之間的時間間隔,bx,k-1,by,k-1,bvx,k-1,bvy,k-1為未知輸入(模型誤差、環境干擾等),wx,k-1,wy,k-1,wvx,k-1,wvy,k-1為噪聲。
同理, 相鄰兩次采樣之間車輛繞質心轉動的角速度也變化不大,因此有:
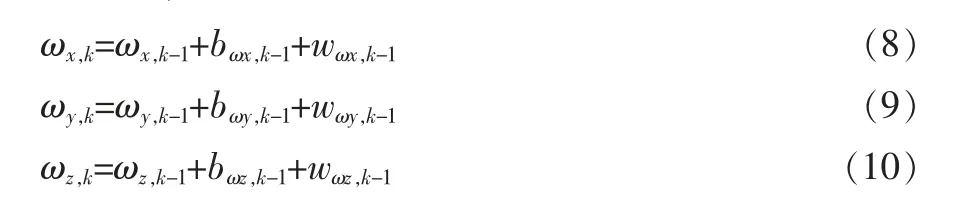
式中:ωx,k,ωy,k,ωz,k為第k 次采樣時載體坐標 系下車輛繞質 心 轉 動 的 三 軸 角 速 度,bωx,k-1,bωy,k-1,bωz,k-1為 未 知 輸 入(模型誤差、環境干擾等),wωx,k-1,wωy,k-1,wωz,k-1為噪聲。
根據歐拉角微分方程[4],車輛行進過程中的航向角、俯仰角和滾轉角可分別由下面三式計算:
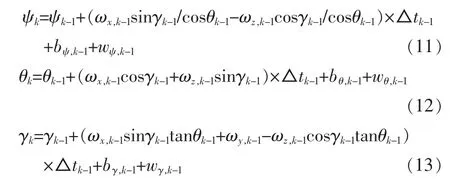
式中:ψk是航向角,即車輛縱軸在水平面的投影與地理北向之間的夾角,偏東為正,偏西為負;θk是俯仰角,即車輛縱軸與縱向水平軸之間的夾角,向上為正,向下為負;γk是滾轉角,即車輛縱向對稱面與鉛垂面之間的夾角,右傾為正,左傾為負。 bψ,k-1,bθ,k-1,bγ,k-1為未知輸入(模型誤差、環境干擾等),wψ,k-1,wθ,k-1,wγ,k-1為噪聲。
1.2 自校準量測方程
根據導航坐標系和載體坐標系之間的變換關系[4],加速度量測方程為:
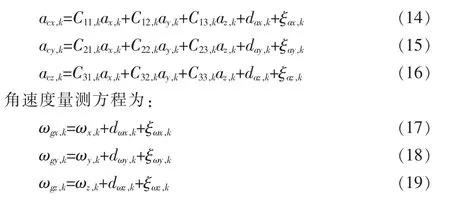
式中:acx,k,acy,k,acz,k為第k 次采樣時載體坐標系下的加速度計量測,dax,k,day,k,daz,k為未知輸入(加速度計漂移、環境干擾等),ξax,k,ξay,k,ξaz,k為噪聲。 ωgx,k,ωgy,k,ωgz,k為第k 次采樣時載體坐標系下的陀螺儀量測,dωx,k,dωy,k,dωz,k為未知輸入(陀螺儀漂移、環境干擾等),ξωx,k,ξωy,k,ξωz,k為噪聲。Cij,k為坐標變換矩陣Ck第i 行第j 列的元素,由下面九式計算[4]:
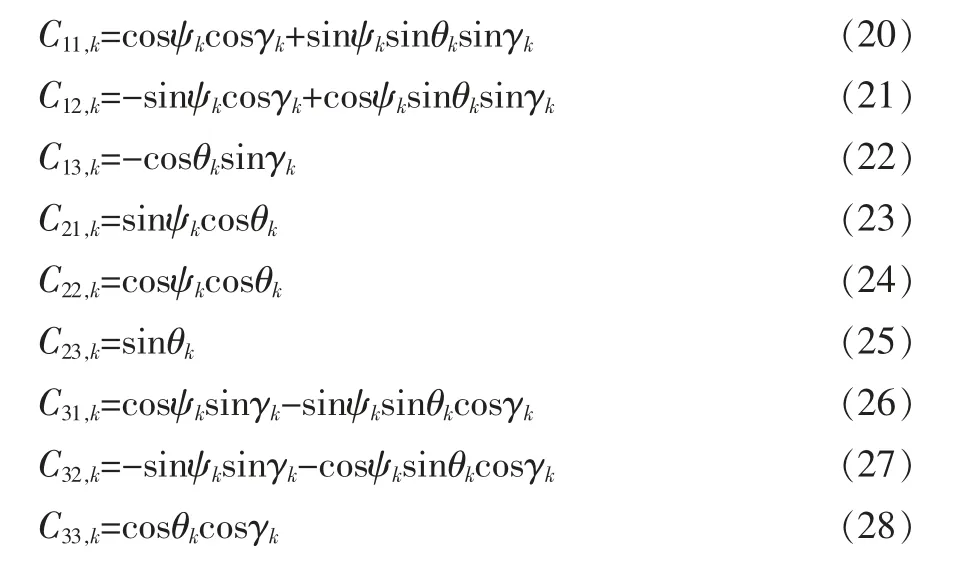
2 基于TOA 的車輛自校準導航方法
下面以超寬帶(UWB)信號為例對基于到達時間(TOA)的車輛自校準導航方法進行討論,其他信號也可同樣處理。
設第k 次采樣時,在位置(xk,yk)處能夠接收到n 個UWB 信號,則基于TOA 的UWB 距離量測方程為:
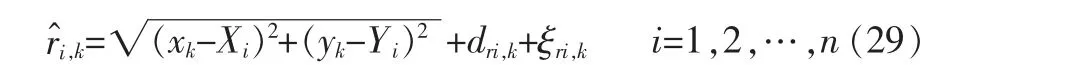

采用文獻[5]中的非線性系統雙未知輸入自校準濾波方法,對狀態方程式(1)~式(13),量測方程式(14)~式(19)和式(29)進行濾波,即為基于TOA 的車輛自校準導航方法。濾波時,可選取視距環境中最小的兩個距離量測值,令其方程中的未知輸入dri,k=0。 也可以采用文獻[5]中的兩步自校準濾波方法來進一步提高濾波的魯棒性和精度。
3 基于TDOA 的車輛自校準導航方法
基于TOA 的車輛自校準導航方法要求基站和標簽的時間完全同步,這在工程實際中有時難以實現。 為此,下面進一步給出只需各個基站之間時間同步的基于到達時間差 (TDOA) 的方法。 仍然以UWB 信號為例對基于TDOA 的車輛自校準導航方法進行討論, 其他信號也可同樣處理。
TDOA 需將基站兩兩分組,第1 個和第2 個基站為一組,第3 個和第4 個基站為一組,以此類推。 下面給出一種以基站距離遠近進行分組的方案:布置n 個UWB 基站(n 為偶數),計算它們兩兩之間的距離;選取距離最小的兩個基站,令其為第1 個和第2 個基站;再在剩下的n-2個基站中選取距離最小的兩個基站, 令其為第3 個和第4 個基站;按照這個規則選取下去,直至最后剩下兩個基站,令其為第n-1 個和第n 個基站。 此時,基于TDOA 的UWB 距離差量測方程為:
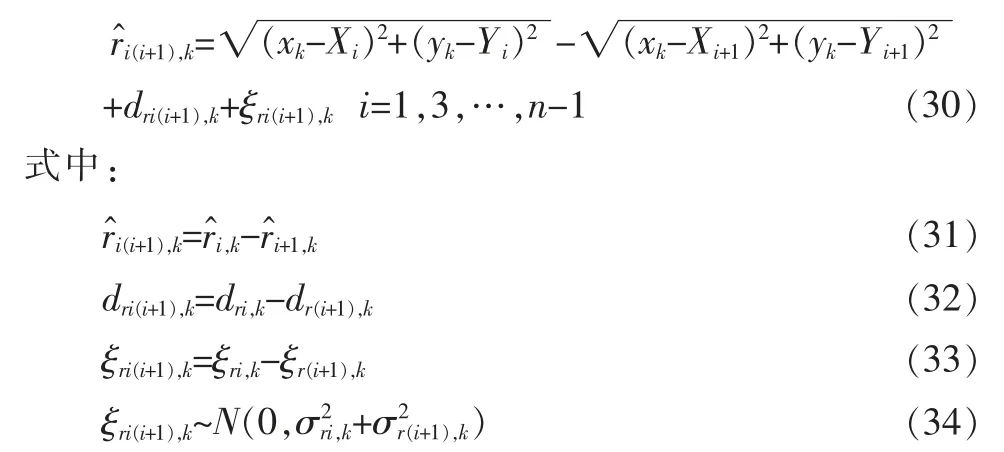
采用文獻[5]中的非線性系統雙未知輸入自校準濾波方法,對狀態方程式(1)~式(13),量測方程式(14)~式(19)和式(30)進行濾波,即為基于TDOA 的車輛自校準導航方法。 濾波時,可選取式(30)所示的n/2 個距離差中絕對值最小的兩個,直接令其未知輸入dri(i+1),k=0。 也可以采用文獻[5]中的兩步自校準濾波方法來進一步提高濾波的魯棒性和精度。
4 基于RSSI 的車輛自校準導航方法
基于接收信號強度指示(RSSI)的車輛自校準導航方法中采用的慣性導航自校準方程仍然為式 (1)~式(19),下面進一步給出RSSI 量測方程。
設第k 次(加速度計和陀螺儀)采樣時,在位置(xk,yk)處能夠接收到n 個熱點(AP)發出的信號,則基于RSSI 的量測方程為[3]:

式中:Si,k為第k 次(加速度計和陀螺儀)采樣時來自第i個AP 的RSSI,(xk,yk) 為此時導航坐標系下車輛質心的位置坐標,(Xi,Yi)為第i 個AP 的位置坐標,r0i為參考距離,S0i為參考距離處的RSSI,ηi為信號強度的路徑損耗系數,dsi,k為未知輸入(量測誤差、非視距誤差等)。 當第i 個AP發出的信號在視距環境中傳播時,直接令dsi,k=0,且這樣的AP 不少于2 個。ξsi,k為零均值服從正態分布的噪聲,即ξsi,k~N(0,σs2i,k)。 考慮到采樣頻率的不同,設加速度計和陀螺儀的采樣頻率是RSSI 信號的采樣頻率的m 倍, 則當k是m 的正整數倍時,濾波的狀態方程為式(1)~式(13),量測方程為式(14)~式(19)和式(35);當k 不是m 的正整數倍時,濾波的量測方程中將不包含RSSI 量測方程式(35)。
同樣,采用文獻[5]中的非線性系統雙未知輸入自校準濾波方法進行濾波,也可以采用文獻[5]中的兩步自校準濾波方法來進一步提高濾波的魯棒性和精度。
5 月球基地自校準定位方法
文獻[3]給出了基于RSSI 的室內自校準定位方法,該方法也可用于基于TDOA 的自校準定位方法。 下面仍以UWB 為例進行討論。
設在位置(x,y)處能夠接收到n 個UWB 信號,則其自校準距離量測方程為:


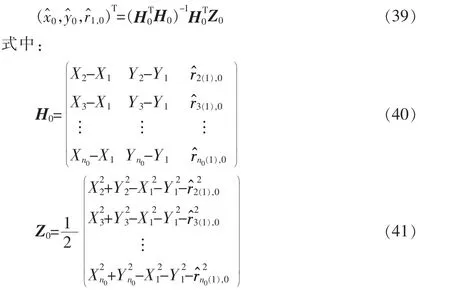


6 實例
現在北京航空航天大學新主樓20m×30m 的一個長方形走廊內進行導航實驗。 在走廊的四個角和四條邊中點布置了8 個WiFi AP。 操控小車沿長方形走廊行駛一圈,實時記錄陀螺儀、加速度計數據和接收到的每個WiFi AP 的三個信號強度平均值。
采用本文方法(自校準秩濾波、自校準無跡濾波)和傳統方法(擴展卡爾曼濾波、無跡卡爾曼濾波)進行計算。計算150 個定位點的導航精度并繪于圖1,且計算其平均值列于表1。
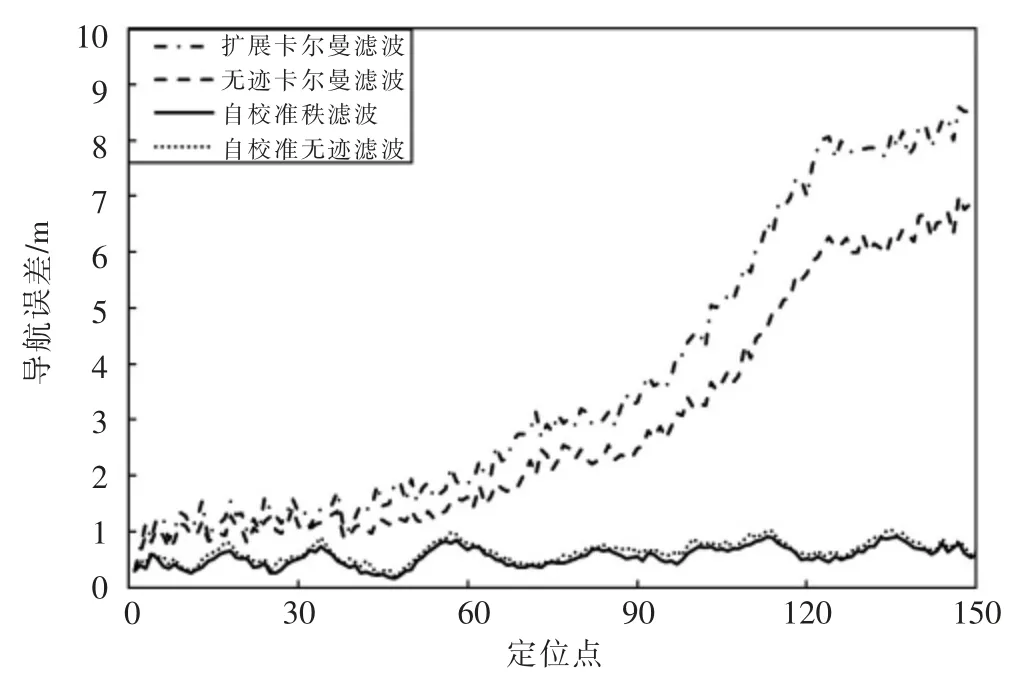
圖1 導航精度比較
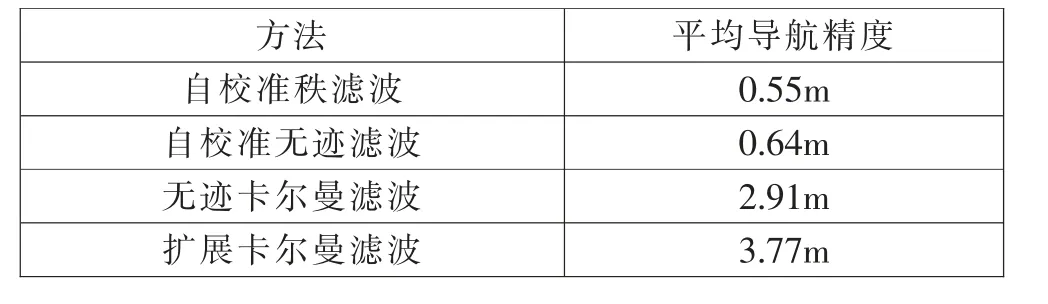
表1 平均導航精度比較
從圖1 可以看到, 本文方法的導航精度比傳統方法的導航精度高且穩定, 而傳統方法的導航精度隨時間的增加而迅速下降。從表1 可以看到,自校準秩濾波的平均導航精度比擴展卡爾曼濾波的平均導航精度提高了5.8倍,比無跡卡爾曼濾波的平均導航精度提高了4.2 倍,這說明本文方法能夠比傳統方法顯著提高導航精度。 自校準無跡濾波的平均導航精度比無跡卡爾曼濾波的平均導航精度提高了3.5 倍, 這說明自校準濾波能顯著提高導航精度。而因為秩采樣屬于最佳采樣,所以自校準秩濾波的導航精度比自校準無跡濾波的導航精度要略高。
7 結論
(1) 提出了車輛自校準導航方法, 包括基于TOA 和TDOA 的車輛自校準導航方法以及基于RSSI 的車輛自校準導航方法,可以實現月球基地車輛的高精度導航。
(2)給出了慣性導航的自校準方程,包括位置坐標、速度、加速度、角速度、角度等的自校準狀態方程和自校準量測方程,能夠有效地對模型誤差、陀螺儀和加速度計的漂移等進行實時修正。
(3)建立了UWB 的距離差量測方程,給出了基站與標簽之間距離差的設計方案及其協方差矩陣, 能夠對量測誤差和非視距誤差等進行實時自校準。
(4) 建立了月球基地自校準定位方法, 包括基于TDOA 的自校準定位方法和能夠將TDOA 與RSSI 相融合的自校準定位方法,可進行高精度定位。
(5) 本文的月球基地車輛自校準導航定位方法也可用于室內(如地下車庫等)的車輛導航定位。

