基于遺傳算法的有機朗肯循環系統換熱器設計優化

任聯章，許俊俊

（1. 中國廣核集團有限公司核電管理部，深圳 518000；2. 蘇州熱工研究院有限公司核安全與運行技術中心，深圳 518000）

1 引言

隨著社會的發展，世界能源短缺問題的日益嚴峻。開發利用中低溫熱能有助于提高能源綜合利用效率，降低能源成本。有機朗肯循環（ORC）發電系統采用氟利昂作為循環工質，具有結構設備簡單、余熱回收效率高等特點，是最有潛力的低品位余熱資源利用技術［1］。ORC通常由循環泵、預熱器、蒸發器、膨脹機、冷凝器等四大部件組成。其中，換熱設備的設計參數不僅影響ORC系統的熱力學性能，還直接影響設備成本［1］［3］。

由于影響換熱器性能的參數結構參數較多，如對于管殼式換熱器，管徑、管長、布管方式等因素都會影響換熱器的性能。目前，換熱器設計多采用經驗方法設計，換熱器設計關鍵參數根據經驗值范圍選取，按照經驗傳熱關聯式計算，通過迭代的方法檢驗設計是否合理。這種設計方法具備一定的經驗性，設計結果不一定是最優的。因此有必要采用新的算法對換熱器進行優化設計。

遺傳算法（Genetic Algorithm，GA），已被人們廣泛地應用于組合優化、機器學習、信號處理、自適應控制和人工生命等領域，它是現代有關智能計算中的關鍵技術［4］。遺傳算法是一類借鑒生物界的進化規律（適者生存，優勝劣汰遺傳機制）演化而來的隨機化搜索方法。它是由美國的J.Holland教授1975年首先提出，其主要特點是直接對結構對象進行操作，不存在求導和函數連續性的限定；具有內在的隱并行性和更好的全局尋優能力；采用概率化的尋優方法，能自動獲取和指導優化的搜索空間，不需要確定的規則，自適應地調整搜索方向。換熱器設計輸入參數不僅包括連續型可量化參數，還包括離散型參數，如管排方式有三角形、正方形和菱形等［5］。此類問題常規優化算法難以處理，遺傳算法的特點比較適合此類換熱器設計中的多參數離散問題求解。

2 優化算法

遺傳算法是把問題參數編碼成染色體，再利用迭代的方式進行選擇、交叉以及變異等運算來交換種群中的染色體的信息，最終生成符合優化目標的染色體。其中染色體對應的是數據或數組，也叫做基因型個體（individuals），一定數量的個體組成了群體（population），群體中個體的數量叫做群體規模（population size），而個體對環境的適應程度叫做適應度（fitness）。基本遺傳算法運算流程見圖1，求解步驟如下：

圖1 基本遺傳算法運算流程圖

（1）編碼：在進行運算之前先將解空間的解數據表示成遺傳空間的基因型串結構數據，即用二進制串的形式表示問題的解。不同的編碼位數和方法對問題的精度和效率有影響。

（2）適應度函數：遺傳算法在運算中僅以適應度來表明個體或解的優劣性，適應度函數用于對個體進行評價，對于簡單的優化問題，通常使用目標函數作為適應度函數。

（3）選擇：從群體中選取優勝的個體，淘汰劣質個體的操作叫選擇。其目的是為了從當前群體中選出優良的個體，使他們有機會作為父代為下一代繁殖子孫。進行選擇的原則是適應性越強的個體為下一代貢獻一個或多個后代的概率大，從而體現達爾文的適者生存的思想。

（4）交叉：交叉操作是指從種群中選擇兩個個體，按照一定的概率將兩個父代個體的部分結構進行交換而得到新的個體。交叉是遺傳算法中最主要遺傳操作，體現了信息交換的思想。其中，交叉操作的使用頻度受到交叉概率的影響，交叉概率過小時，遺傳算法可能出現局部收斂問題。較大的交叉概率可以增強算法開辟新的搜索區的能力，避免局部收斂，但同時也降低了搜索效率。交叉概率一般值在0.4～0.99之間。

（5）變異：遺傳操作是指從種群中隨機選擇兩個個體，按照一定的概率改變其二進制串結構數據中某個串的值而得到新的個體。和生物界一樣，遺傳算法中發生變異的概率很低，通常取值在0.001～0.01之間。

3 換熱器設計計算模型

本文針對ORC系統常用的預熱器、蒸發器和冷凝器建立熱力學計算模型，選用常用的管殼式換熱器進行計算。

3.1 預熱器模型

（1）管程計算

管程計算采用的是水平光管計算模型［6］。

① 程單相傳熱計算，采用公式如下：

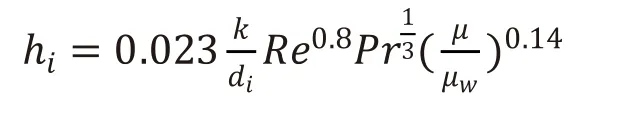
Re——雷諾數，，無因次；

Pr——普朗特數，

hi——管內對流傳熱系數，

k——總傳熱系數，

di——管內徑，m；

μ——動力粘度，Pa·s；

μw——20℃時水的動力粘度，Pa·s。

②管程單相壓降計算模型

管殼式換熱器管程壓降主要包括兩部分：直管內摩擦壓降和各程回彎處的局部阻力降。其中直管內摩擦阻力引起的壓降公式：

式中△pt——直管摩擦壓降；Pa；

fi——摩擦因數，無因次。

層流時：圓管內，

湍流時fi是Re和管壁粗糙度的函數。對光滑管而言，

（2）殼程計算

殼程的計算采用的是Bell-Delaware方法［6］，其假定全部殼程流體都是以純錯流的形式通過理想管排（即沒有漏流、旁流等的影響）的，在此假設下求得理想管排的傳熱系數hideal和壓降△PBi，然后依據具體的換熱器結構參數及操作條件，引入各項修正系數進行傳熱和壓降的計算。

①殼程單相傳熱計算模型

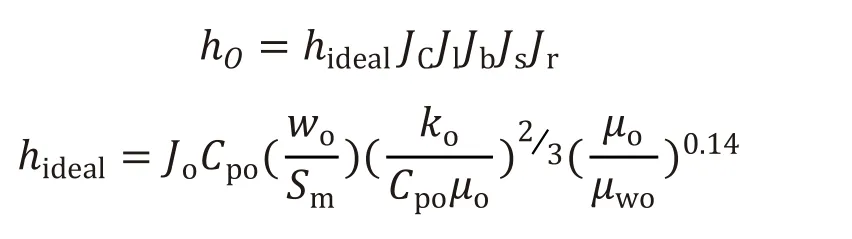
式中

hideal——理想管排殼程傳熱系數， W/（m2·℃）；

ho——殼側對流傳熱系數，W/（m2·K）；

Jc— —折流板形體校正因數，無因次；

Jl——折流板漏流校正系數，無因次；

Jb——旁流校正因數，無因次；

Js——進、出口段折流板間距不等時的校正系數，無因次；

Jr——低雷諾數下逆向溫度梯度校正系數，無因次；

Jo——殼程理想管排的校正系數，稱J因數，無因次；

Sm——流通截面積，m2；

wo— —殼程質量流量，kg/s；

μwo——以壁溫為定性溫度的動力粘度，Pa·s；

C po’ ko’μo— —以殼程流體溫度為定性溫度而確定的流體物性，Cpo比 定壓熱容，J/（kg·K）；ko熱導率，W/（m·K）；μo動 力粘度，Pa·s。

②殼程單相壓降計算模型

△Po— —殼程壓降，Pa；

△PBi— —理想管排錯流區壓降，Pa；

△Pwi——理想管排圓缺壓降，Pa；

Rb——旁流影響壓降的校正因數，無因次；

Rl——漏流影響壓降的校正因數，無因次；

Rs——進、出口段板間距不等時對壓降影響的校正因數，無因次；

Nc——每一錯流區內的管排數；

Ncw——圓缺區內有效管排數。

其中，理想管排錯流區的壓降△Pbi

式中

fi——理想管排摩擦因數，無因次；

ρo——殼程流體的密度，kg/m3。

理想管排圓缺區的壓降△Pwi

當Reo≥100時

當Reo＜100時

式中

do——管外徑，m；

Dw——圓缺區當量直徑，m；

Pt——管心距，m；

Sm——中心線或靠近中心線錯流區流通截面積，m2；

Sw——圓缺區流通截面積，m2。

3.2 蒸發器模型

蒸發器采用的是管內蒸發的方式，殼程為單相熱流體，殼程傳熱和壓降計算模型與預熱器相同。

（1）管程蒸發傳熱計算模型

管程蒸發傳熱采用雙機理法進行管內流動沸騰傳熱的計算。雙機理法就是同時考慮兩相強制對流機理和飽和泡核沸騰機理。表達式如下：

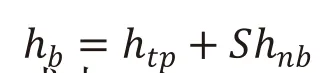
式中

hb——管內流動沸騰傳熱系數，W/（m2·K）；

htp— —兩相強制對流傳熱系數，W/（m2·K）；

hnb——泡核沸騰傳熱系數；

S——泡核沸騰抑制因數。

而兩相強制對流傳熱系數

式中

Ftp——對流換熱強化因數，無因次，是Martinelli參數Xtt的函數；

hl——（液體單獨存在時求得的）液體對流傳熱系數，W/（m2·K）。

其中Ftp的關聯式：

式中

x——蒸汽干度，即質量氣化率，為一質量分率，無因次；

Xtt——Martinelli參數，無因次。

hl是液體單獨存在而求得的液體傳熱系數。

式中

Gt——總（包括氣相和液相）質量流速，kg/（m2·s）；

μl——兩相中液體的動力粘度，Pa·s；

Cpl——液體的比定壓熱容，J/（kg·K）。

泡核沸騰傳熱系數采用Forster-Zuber式：

式中

λ——汽化或冷凝潛熱，J/kg；參數，無因次；

Tw——壁溫，℃；

Ts——液體飽和溫度，℃；

△ps——與△Ts相對應的飽和蒸氣壓差，△ps=p-ps，Pa。

其中，抑制因素S采用曲線擬合，計算公式為：

當Retp＜32.5

當Retp＞32.5

從式中可見，當流量為零時，S=1；當流量趨于無限大時，S→0。

（2）管程蒸發壓降計算模型

管內兩相流壓降計算采用公式如下：

式中

△ptp——在有限管長△L內的兩相流壓降；

△ptps——靜壓頭引起的壓降，Pa；

△ptpm——動量變化引起的壓降，Pa；

△ptpf——摩擦損失引起的壓降，Pa。

其中，摩擦損失所引起的壓降是最主要的，比其他兩項都大。用來描述摩擦壓降的主要流動模型有：均勻流模型和分離流模型。

蒸發器管內蒸發采用的是分離流動模型。分離流動模型即設想每一相在重力、剪力及其他參數的影響下，兩相各以不同的流速流動，并考慮兩相間的相互作用。按此模型，兩相流摩擦壓降為：

式中

△pl——假定管內只有液相存在時計算所得的壓降，Pa；

△pv——假設管內只有氣相存在時計算所得的壓降，Pa；

φl——兩相流液相因子，無因次，是Martinelli參數X的函數；

φv——兩相流氣相因子，無因次，是Martinelli參數X的函數。

由上式可知，按液相或氣相條件可求算兩相流摩擦壓降：

式中f1——范寧摩擦因數，是雷諾數的函數。

式中fV——范寧摩擦因數，是雷諾數的函數。

在圓管內，當Rel≥2100時

同理，ReV≥2100時

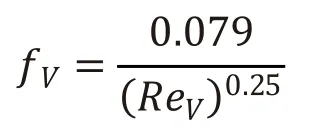
當Rel＜2100時

或ReV＜2100時

上面各式中

各種不同條件下的C值如下表1所示

表1 系數C取值參數表

3.3 冷凝器模型

冷凝器采用的是殼程冷凝的方式，管程為單相冷流體，管程傳熱和壓降計算模型與預熱器相同［6］。

（1）殼程冷凝傳熱計算模型

式中

ρl——凝液的密度，kg/m3；

ρv——蒸汽的密度，kg/m3；

g——重力加速度，m/s2；

N——管束垂直列上的管數，無因次；

kl——凝液的導熱率，W/（m·K）；

μl——兩相流中液相動力粘度，Pa·s。

（2）殼程冷凝壓降計算模型

殼程壓降計算采用的是兩相流動壓降計算中的均勻流動模型［6］。均勻流就是把兩相流體當作一股虛擬流體，假定兩相混合物具有相同的流速并用兩相的物性平均值來表達其物性。

均勻流動模型

式中ρtph——均勻流的密度，kg/m3；

因為均勻流的s=1，因此均勻流的密度可用下式計算：

式中ftp——兩相流摩擦因數，無因次。可用單相流的伯拉修斯方程的形式來表達：

式中a，m——系數，無因次。a=1.33；m=0.5。

μtp— —兩相混合物粘度，Pa·s。

采用以下公式來計算兩相混合物粘度：

式中μl——兩相流中液相動力粘度，Pa·s；

μv——亮相流中氣相動力粘度，Pa·s。

4 模型驗證

使用某公司ORC實驗平臺使用的換熱器參數進行驗證。將該換熱設備結構設計參數，帶入到該換熱器計算模型中，得到的計算結果見表2。與實驗臺換熱器數據對比顯示換熱面積相對偏差在5%以內。

?

?

5 ORC換熱設備優化設計

5.1 目標函數

換熱設備換熱面積是關系換熱器制造成本的關鍵指標，換熱面積越小，換熱器成本越低。本文選取換熱器面積作為該優化計算模型中遺傳算法的優化目標。

5.2 約束條件

本模型根據計算的情況，遺傳算法求解主要參數設置如下：種群大小100，交叉概率0.85，變異概率0.001，適應度值收斂容忍限≤10-10，最大遺傳代數500代。并選取的換熱器優化參數如下：

表3 GA-換熱器優化變量及取值范圍

5.3 收斂條件

為保證結算結果滿足可靠，給定GA收斂條件：①計算停止的代數小于最大終止代數；②或者適應度值變化小于最大容忍限。否則，需要調整GA求解參數重新求解。圖2給出了求解過程最優解隨著遺傳代數收斂的過程。

圖2 最優解隨遺傳代數收斂過程

5.4 優化結果

采用遺傳算法對該換熱器優化設計模型進行求解。得到換熱器優化結果與原設計數據對比見表4所示。根據GA遺傳算法優化的結果，預熱器減小了20.54m2，相對減小了17.12%；蒸發器減小了171.90m2，相對減小了17.81%；冷凝器減小了152.01m2，相對減小了14.62%。

對比優化后模型參數，管程數和殼程數與原設計一致，管長、管徑、管排方式、殼內徑、折流板間距系數等均有調整。總體參數上，預熱器、蒸發器、冷凝器的管長更長，管程傳熱管總數有所減少，管排方式優化未菱形或正方形排列。分析計算結果表明，優化后的管排參數和結構有助于管程和殼程層流，流動雷諾數有較大提升，從而提高了傳熱管兩側對流傳熱系數，總傳熱系數增加，所需的換熱面積減少。

表4 優化結果與初始設計結果對比

6 結論

本文通過ORC系統的預熱器、蒸發器和冷凝器建模，并采用實驗平臺換熱設備作為驗證，計算換熱面積偏差在5%以內，模型計算結果相對可靠。采用遺傳算法進行優化求解，選取管長、管徑、殼內徑、折流板間距系數、管排方式、管程數、殼程數等設計參數作為優化變量。優化結果表明，換熱器初始設計總計換熱面積為2125m2，優化后面積為1780.55m2，總換熱面積相對減小了16.21%。但由于采用單目標優化，僅以最小換熱面積為優化目標，該模型傳熱管壓力損失誤差較大，還有進一步優化空間。本文研究結果表明使用遺傳算法將換熱器設計中的結構參數作為優化變量，不僅可選擇連續型變化的參數，也可用于離散型參數的優化，為換熱器設備等工業設備的設計選型問題提供了一種優化計算方法，對ORC系統設計優化提供新的思路。