高壓電源應用中LCC諧振變換器的研究綜述

汪邦照，劉艷麗，汪方斌，王 磊

（1.合肥華耀電子工業有限公司，安徽 合肥 230031；2.安徽建筑大學 機械與電氣工程學院，安徽 合肥 230601）

0 引 言

目前，國內采用的大功率高壓電源基本工作于電流斷續模式，電力電子變換器處于軟開關工作狀態，開關損耗大大降低。但另一方面，工作于電流連續模式下的高壓電源能大幅度提高諧振變換器的輸出電流從而提高輸出功率[1]。Alstom公司的科技人員在文獻[2]中也介紹了大功率高壓電源的電流連續工作模式，并提出了一種減少開關損耗的最優化算法。可見，高壓電源的電流斷續和電流連續工作模式各有其優點，鑒于處于電流斷續工作模式下的高壓電源已有很豐富的開發經驗，因此本文僅對電流連續工作模式下高壓電源的分析方法、優化算法和控制方法展開討論。

大功率和中高壓電源的諧振信號變換器多為三相LCC串并聯方式結構（如圖1所示），三相LCC串并聯結構諧振變換器同時兼顧了串聯和三相并聯諧振變換器的優點，具有效率高、特別是其功率密度高能將其體積做到很小[3-5]。文章介紹了可用于這種拓撲結構的諧振電路的幾種分析和設計方法，這些方法都能建立LCC串并聯諧振電路的數學模型，然后，基于數學模型可以用仿真手段分析電路的性能，從而指導電路設計，可在后期的實驗環節節省大量人力和財力。

并且研究發現，LCC串并聯諧振電路是強非線性系統，電路中大部分參數是相互關聯的，針對不同的電路特性對元件的選擇有一定的限制，這些因數導致了這種拓撲結構的電路分析和設計過程十分繁瑣。為了根據電路的設計要求找出一個最優的設計方案，本文提出了一種基于Pareto的多目標遺傳算法SPEA2，相對于傳統的優化算法，遺傳算法SPEA2在諧振電路性能優化應用中有明顯的優勢。

最后，文章還特別提到了一種適用于諧振控制電路的一種最優軌跡驅動控制設計方法，該控制方法在系統信號響應時間、穩定性、短路時的承受能力均有很好的控制能力。

圖1所示Lr為包含了變壓器的漏感串聯諧振電感，Cr為串聯諧振電容，Cp為包含折算后的分布電容的并聯諧振電容。

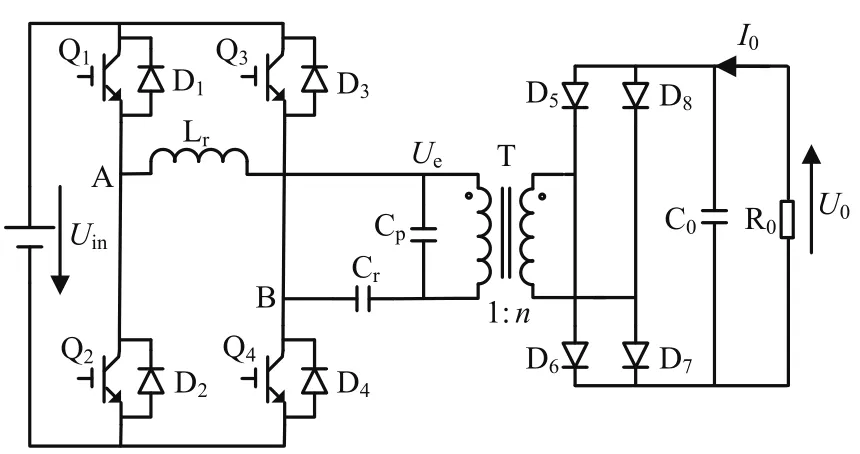
圖1 高頻直流電源諧振電路拓撲

1 LCC諧振變換器的分析方法

1.1 時域分析法

LCC諧振電路常見的6種諧振狀態如圖2所示。根據這6種諧振狀態，用歐姆定律即可求出每個時段內諧振電流和電容電壓為狀態變量的時域方程。

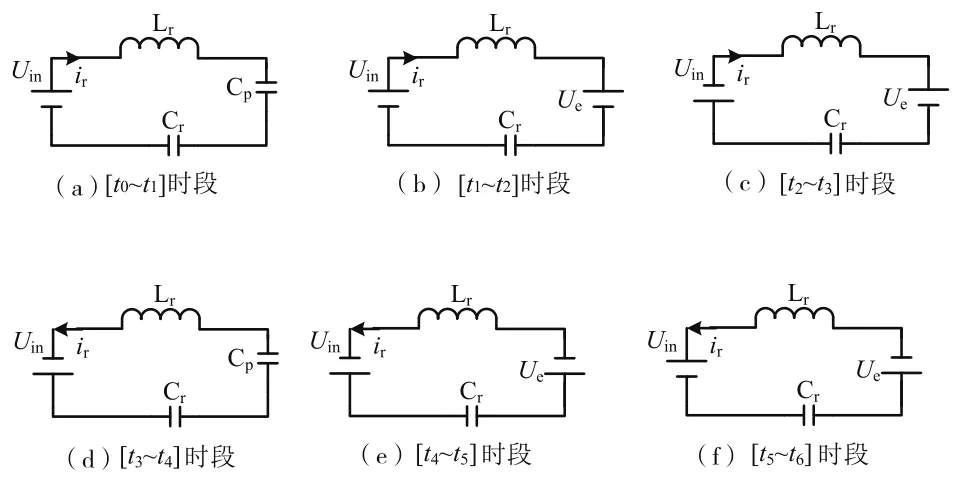
圖2 LCC諧振電路的6種諧振狀態

時域分析方法的優點：精確度最高。缺點：數學模型很復雜，而且通過時域數學模型分析電路穩態性能比較困難。

1.2 狀態平面分析法

狀態平面分析法由Oruganti R.和 Lee FC.于1988年提出，它是建立在時域數學模型基礎上描述諧振電路規范化狀態變量變化軌跡的一種分析方法[6]。簡單點說，就是通過這種方法，可以把時域數學方程中狀態變量的變化軌跡用圖形描述出來。

如圖3所示以電容電壓和諧振電流為狀態變量，建立了狀態圖，即LCC諧振電路的穩態軌跡。圖2中的每個諧振時段對應于圖3中的一個圓弧，例如：圖2（a）時段對應U′CN(i′CN)坐標軸AB段圓弧；（b）時段對應UCN(iCN)坐標軸CD段圓弧；（c）時段對應于UCN(iCN)坐標軸DE段圓弧。另外，圖2（d）、（e）、（f）時段與圓的下半周對應。

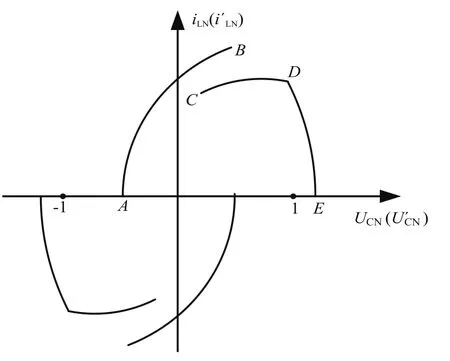
圖3 LCC諧振電路的穩態軌跡

狀態平面分析法優點：把原來的時域模型中狀態變量的變化軌跡圖形化了，比較直觀，而且精確度和時域模型一樣高。缺點：建模過程很復雜，電路穩態性能通過此方法仍較難分析。

1.3 基波分析法

基波分析法是一種廣泛應用于諧振電路的近似分析方法。分析過程是：取電流基波分量和高頻變壓器一次側交流電壓，得到諧振變換器的等效電路（采用正弦穩態分析方法），如圖4所示為其等效電路。然后在等效電路基礎上推導數學模型，最后根據推導的數學模型確定一種符合系統設計需要的最佳交流電路參數。

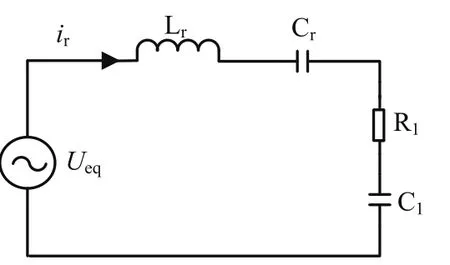
圖4 LCC諧振電路的等效電路

圖4中，R1和C1分別為原電路變壓器側等效電阻和電容。

基波分析法的優點：容易建模，通過此分析方法可以分析電路穩態性能，并用于指導電路設計。此法缺點：很難分析電路暫態過程，且分析精確度不高。

1.4 動態相量分析法

1991年SANDERS SR等人提出動態相量法[7]，目前，國內外許多技術專家已在實際應用進行了研究，如：電力系統和電力電子電路[8-11]，并證明了這種動態相量法具有數學仿真快和精度高等諸多優點。

動態相量法的基本建模原理如下文所述。

對于時域中波形是連續并且變化快速的信號x(τ)，波形可以通過傅里葉級數描述為

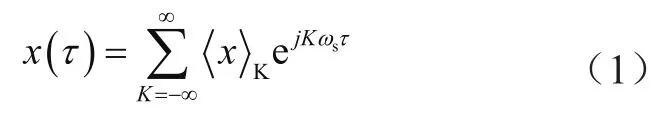
式中，ωs=2π/T0；時間間隔τ∈(t-T0,t]；〈x〉K為第K階“動態相量”，它是時間的函數。

第K階動態相量的微分特性可描述為

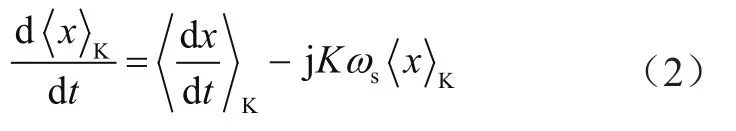
基于以上動態相量的基本理論，即可成功建立3種數學模型：基于動態相量LCC諧振電路的大信號模型、基于動態相量LCC諧振電路的穩態模型和基于動態相量LCC諧振電路的小信號模型。其中，大信號模型可用來分析系統的暫態過程；穩態模型可用來分析穩態時系統的電路特性；在頻域內分析系統動態響應可以用基于動態相量LCC諧振電路的小信號模型進行分析。

（1）大信號模型的仿真結果

用Matlab 對LCC諧振電路大信號模型進行仿真。電路仿真時的條件描述如下：電路仿真時的算法采用ode23，仿真時的步長參數為1 μs，電路仿真參數為：Uin=100 V；R0=30 Ω；Lr=100 μH；Cp=Cr=1 μF；C0=47μF。

算例：如圖5所示，在3 ms時刻，開關頻率fx由25 kHz躍變到20 kHz時，諧振電流和輸出電壓仿真曲線如圖5所示。可見在開關頻率發生躍變時，動態相量曲線很好地包絡了時域仿真曲線。

圖5 開關頻率躍變時的動態相量模型與時域模型波形比較

（2）穩態模型仿真曲線

按照穩態模型可求得電壓/電流傳輸比表達式：

式中，Q為電路品質因數；θss為Cp充電時段對應的角度；Im為諧振電流幅值；fm為開關頻率與諧振頻率比值。

根據式（3），通過計算機進行仿真后即可得到在品質因數為1和品質因數5時的電壓傳輸比關系曲線。每組曲線里又有不同θss，如圖6所示。

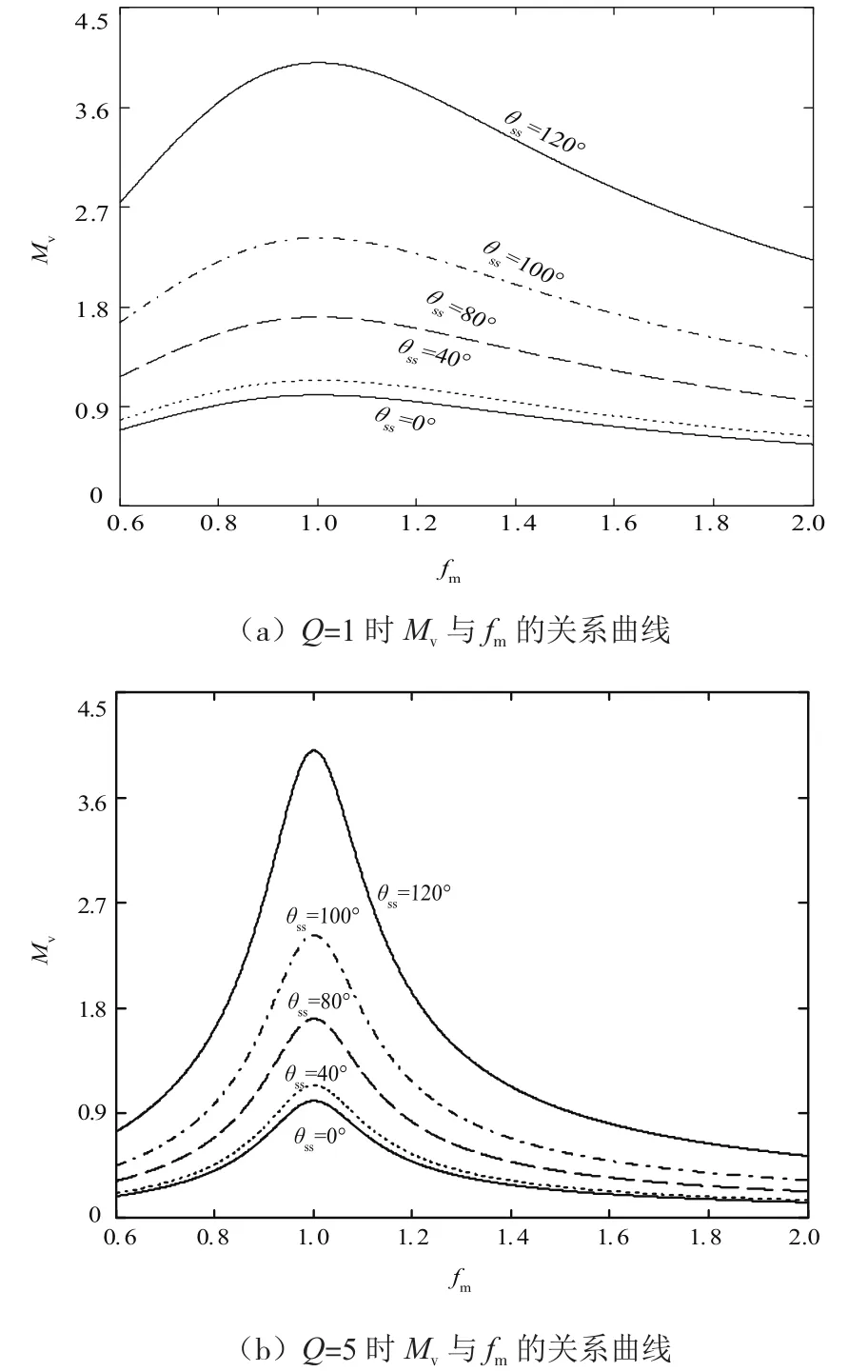
圖6 品質因數不同時電壓傳輸比的關系曲線

根據式（4），電流傳輸比關系曲線如圖7所示。

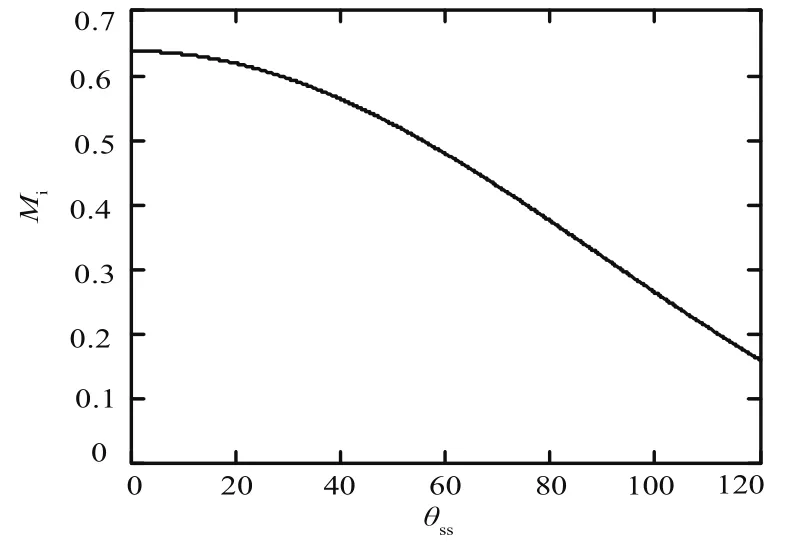
圖7 電流傳輸比的關系曲線

動態相量法優點：（1）建模容易；（2）仿真精確度介于時域分析法和基波分析法之間，但仿真速度比時域模型快得多（大約20多倍）；（3）基于動態相量法建立的大信號模型可用于分析電路的暫態過程，而穩態模型可用于分析電路性能并指導電路設計；（4）動態相量法對LCC諧振電路的建模為其小信號分析打下了基礎，進而全面了解系統的動態響應特性；（5）在仿真環節就已經掌握了電路的暫態和穩態性能，為電路的設計參數的選擇服務。

缺點：隨著諧波次數的增加，諧振電路分析的精確度也增高，但是數學模型的建立過程也越來越復雜。

2 LCC諧振變換器的多目標優化算法

2.1 基于PARETO的多目標遺傳算法

1985年第一個多目標演化遺傳算法首次出現，該算法是基于向量評估的遺傳算法（Vector Evaluated Genetic Algorithm，VEGA）。后來許多學者在多目標優化研究領域探索的同時提出了多種解決方法。例如，比較常用的基于Pareto遺傳算法[12-14]有：仿Pareto遺傳算法（Niched Pareto Genetic Algorithm，NPGA）和增強Pareto進化算法（Strength Pareto Evolutionary Algorithm，SPEA）。多目標優化遺傳算法很適合LCC諧振電路的設計。它的主要特點是只需要提供目標函數的信息，就可找到最優解（對搜索空間不連續不可微分的也適用），因此選擇遺傳算法作為LCC諧振電路的多目標優化方法是合適的。

多目標優化問題的數學描述如下：

式中，X為決策變量空間；x為帶有n個決策變量的向量；Y為目標函數空間；y為帶有n個目標函數的向量；e(x)為m個約束函數。

多目標優化的主要問題是：多個目標之間相互約束，對其中一個目標優化就會損害另一個目標的利益，因此很難客觀地來評價多參數目標解的優劣。

如圖8所示為SPEA2算法流程圖。圖中，T為遺傳算法中最大的進化次數。

圖8 遺傳算法SPEA2流程

2.2 算法驗證

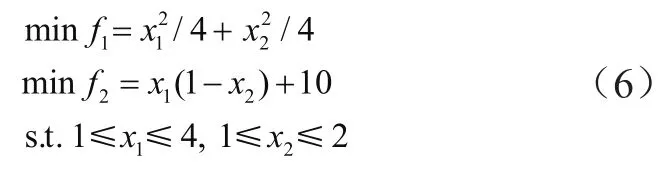
式（6）為SPAE2算法驗證算例。

基于SPAE2算法獲得的Pareto前沿如圖9所示。本算法采用Matlab仿真，源程序代碼中初始種群個體數目為50，最大遺傳代數為100。可以看出，采用此算法能獲得大量均勻的Pareto最優解集。

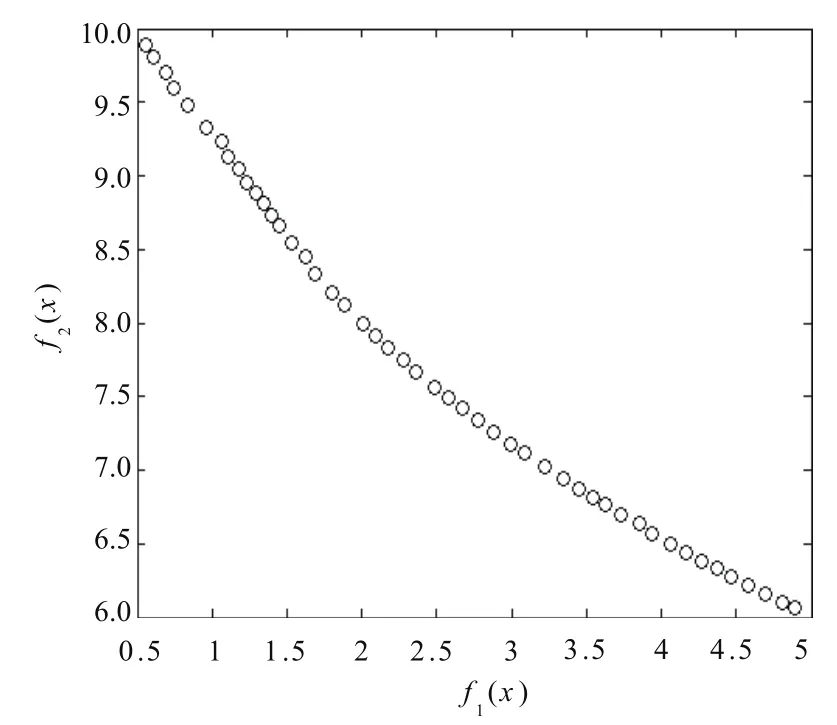
圖9 遺傳算法SPEA2獲得的Pareto前沿

2.3 在LCC諧振電路設計中用多目標優化算法的原因分析

國外已有在LCC諧振電路中設計中用優化算法的先例，如Alstom公司的技術人員在大功率高壓電源的電路參數設計中為減少開關損耗而用到了遺傳優化算法。但值得指出的是，他們用的僅僅是單目標優化算法，而本文提到的多目標優化算法能以多個優化對象為目標進行優化。

多目標優化算法用于LCC諧振電路優化設計的優點：（1）為了達到設計目的，以其設計目標為優化對象進行仿真計算后立即可得到一組供技術人員參考的電路參數；（2）在實驗環節可以節省大量的人力和財力投入。

3 LCC諧振變換器的最優軌跡控制

最優軌跡控制法由Oruganti R.和 Lee F.C.于1985年提出[15,16]。他們在文獻[16]中對比串聯諧振電路的變頻控制、電容電壓控制、二極管導通角控制和最優軌跡控制。從系統響應時間、穩定性、短路承受能力等方面對這4種控制方法進行比較，最后得出最優軌跡控制在這些方面均處于優勢的結論。但值得指出的是，雖然最優軌跡控制有很多優點，但它在應用上實現比較困難。

就大功率高壓電源應用場合的特殊性來看，對高壓電源的要求是抗短路能力強，且在火花發生以后為了快速恢復電場能量還要求系統響應時間短。由此可見，最優軌跡控制將來不失為大功率高壓電源諧振變換器控制方法的一種最好選擇。

簡單地說，最優控制法則就是制定控制命令，這個控制命令主要任務由DSP進行最優開關時間的計算，即計算出什么時候開關管導通或最佳關斷時刻。此控制方法是以諧振電路電感電流和電容電壓為狀態變量，從而建立狀態圖，在狀態平面法建模的基礎上實施。期望在最短的時間內實現兩個不同穩態軌線的轉換，即達到它們期望的穩態軌跡并保證良好的動態性能，從而減少暫態振蕩。其控制框圖如圖10所示。

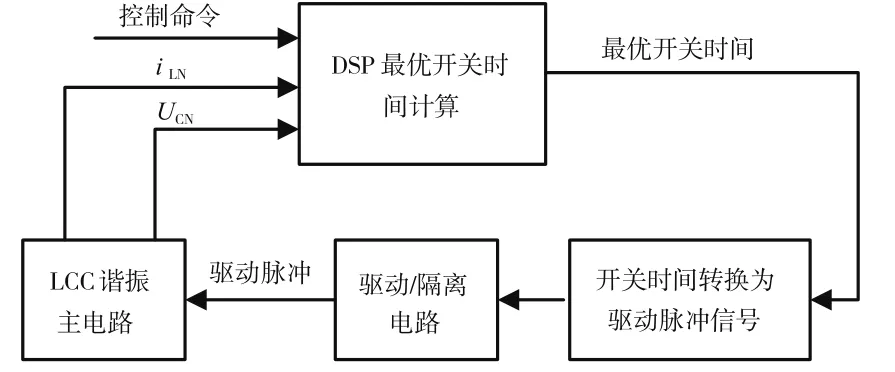
圖10 最優軌跡控制框圖

4 結 論

文章介紹了電流連續模式下LCC諧振變換器的幾種分析方法，提到了可用于這種強非線性電路拓撲結構的一種多目標優化算法，最后介紹了一種最優軌跡控制方法。這些分析方法、優化算法和控制方法已有一些專家和研究人員展開了研究，其研究目的在于改善LCC諧振電路的系統性能，指導電路設計和調試，以達到預期的設計和控制目標。文中LCC諧振電路的分析方法、控制方法和多目標優化算法對于推進我國大功率高壓高頻電源應用領域的研究和實踐有一定的參考價值。