數據驅動型的維修任務分配方法

摘要：采用數據驅動方法來解決維修生產環境中復雜的任務分配問題。首先利用多種細致的量化方法制訂一套詳細而客觀的評分系統，然后采用并行計算環境下的蒙特卡洛樹搜索來快速搜尋各種有價值的分配組合方案，最后從探索的樹結構中選擇最佳的方案來完成任務的分配。該方法不僅使數據科學技術在實際生產過程中得到落地，而且還取得了不錯的效果。

關鍵詞：數據驅動；大數定律；余弦定理；馬爾科夫決策過程；蒙特卡洛樹搜索

Keywords：data driven；law of large numbers；cosine theorem；MDP；MCTS

0 引言

通常在數學模型的設計上，只要數據量足夠，就可以用若干個簡單的模型取代一個復雜的模型，這種方法被稱為數據驅動方法。該方法在數據量不足時找到的模型可能會與真實模型存在一定的偏差，但是在誤差允許的范圍內可以認為與精確的模型是等效的，這在數學上是有根據的。從原理上講，類似于切比雪夫大數定律[1]，如公式（1）所示。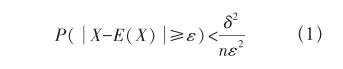

其中，X是一個隨機變量，E（X）是該變量的數學期望值，n是實驗次數（或者是樣本數），ε是誤差，δ2是方差。這個公式的含義是：當樣本足夠多時，一個隨機變量和它的數學期望值之間的誤差可以任意小。

在今天的IT領域中，越來越多的問題可以用數據驅動方法來解決。當一個問題暫時不能用簡單而準確的方法解決時，可以根據以往的歷史數據，構造很多近似的模型來逼近真實情況。2016年谷歌的AlphaGo[2]就是數據驅動方法對機器智能產生作用的最佳案例[1]。

1 理論分析與解決思路

1.1 理論分析

航線工作復雜多變，如果從任務序列上來審視，會發現對序列上的第n個任務如果執行了行動an（安排了具體的人員），就會導致整個團隊的狀態sn（員工工作量狀態、人員任務的匹配狀態等）發生了變化，同時這個變化后的狀態sn+1又會影響到接下來的分配行動an+1，那么分配過程就可以用一條狀態—行動鏈條[3]表示（見圖1）。

圖1所示的狀態序列稱為馬爾科夫鏈，這個鏈條包含了狀態和行動的依次相互轉換。如果用嚴謹的方式表述，策略是一種映射，它將團隊的狀態sn映射到一個行動集合的概率分布或概率密度函數上。可以認為管理者對每一個行動都有一定的執行可能性，且行動的評價越高，執行的概率越大，形式化來說就是在第n個任務選擇最優的分配行動[3]，如公式（2）所示。

1.2 解決思路

1）狀態的定義方法

把工作團隊看成一個整體S，這個S的各個屬性需要有客觀的量化方法來計算，主要包括：人員與任務的匹配程度Sfit、人員默契程度Stacit、人為因素指標Shf、人員分配合理程度Slogic等。

2）任務分配的綜合評價方法

屬性指標之間關聯性較強，為了保證每個指標數據都能對評估有貢獻而不被稀釋，采用非線性綜合評價模型[5]，如公式（3）所示。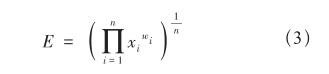

其中，E為評估分數，xi為指標量化數值，wi為該指標的權重系數。任務分配結束后計算各個屬性的分值，然后匯總評估該次分配方案的分數。

3）策略好壞的度量方法

現實中不可能遍歷所有的行動，根據大數定律啟發，一個行動的好壞可以由其后產生的所有行動樣本期望值來進行估計，并且樣本數越大越接近真實值。

2 狀態屬性的量化方法

2.1 人員與任務匹配程度指標

Sfit指標采用余弦定理[6]來量化人員與任務之間的匹配關系。具體的計算過程可以參考筆者另一篇論文《針對大量業務數據的分析方法》[7]中的人員成分分析內容。以該任務的最優人員為基準，其他人通過計算向量角的余弦值來表示與任務的匹配程度。對已經完成的任務分配方案計算總體匹配程度，如公式（4）所示。

其中，ωc、ωn、ωs分別為重要任務、普通任務和簡單任務在總體匹配程度中所占的比例，且ωc+ωn+ωs=100%。μc、μn、μs分別為所有的重要任務、普通任務和簡單任務的配給人員任務匹配系數均值。對于VIP任務或者非常重要的任務，計算時可以對相應的人員任務匹配系數進行指數加權處理，增加系統的“懲罰”力度。

2.2 人員默契程度指標

Stacit指標與員工之間的歷史合作次數直接相關，主要采用3種評判標準：1）歷史合作次數np；2）近期合作次數nr；3）近期連續合作次數ns。計算時將上述3種數值和對應的權重相乘求和得到標準化的合作次數W，然后利用邏輯回歸模型[6]對W進行激活處理，得到人員之間的默契程度數值，最后將各合作人員之間的默契程度數值取平均值，得到該任務的人員默契程度數值，如公式（5）和（6）所示。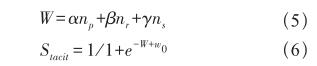

其中，α為遺忘系數（取值小于1.0），β為保持系數（一般取值等于1.0），γ為強化系數（取值大于1.0）。w0為判定人員默契的最少合作次數，該參數是超參數，可以依據現實情況自行設置。

2.3 人為因素指標

Shf指標分析人員的工作強度和間歇時間兩個方面的情況。首先，將員工的普通和特殊工作時長整合為標準的工作時長Tnorm，然后通過各自的折線函數F（t）得到工作強度數值，如圖2所示。間歇情況通過系數ω對工作強度數值來進行影響，ω為間歇時間滿足人為因素的程度，如公式（7）和（8）所示。

其中，Q為任務分配方案中參與人員的人為因素指標數值，對Q中m個最小值求平均，便得出了該次任務分配方案的總體人為因素指標，其中m的數值需要遠小于人員數量。

2.4 人員分配合理程度指標

Slogic指標衡量員工是否有充裕時間完成分配的工作。正常生產過程中，一人同時負責多項任務或者需要跨多機位同時工作是不允許出現的狀況，如果員工工作量序列中出現類似情況，就需要對任務分配方案進行“懲罰”處理。當某員工同時負責的任務個數超過設定的容忍極限值時，就直接將合理程度Slogic置0.0，若沒有超過就按照超額工作時長的線性關系進行衰減處理。最后，與人為因素指標計算方法類似，取該次任務分配人員中合理程度數值最小的m個人的均值作為該分配方案的總體合理程度指標。

3 任務分配搜索方法

3.1 搜索原理

任務分配系統的核心方法是蒙特卡洛樹搜索MCTS[3]，該方法大量使用于博弈類問題[8]。對于那些由于計算過于復雜而難以得到解析解或者根本沒有解析解的問題，蒙特卡洛樹搜索是一種有效的求出數值解的方法。整個過程包含4個過程，分別是選擇、擴展、仿真和回傳。

在實際計算操作過程中，任務列表按照時間順序劃分為搜索樹的層級，每層的節點就是當前任務分配方法，也叫分配節點，整個搜索樹的深度就是需要分配的任務數量，廣度就是所有可能的方案數量，如圖3所示。

按照任務的順序從整個搜索樹的根節點開始往下搜索，根據ε-greedy算法[3]隨機生成新的節點或者選取最優的節點作為子節點。完成所有任務分配后，調用評估系統對任務分配方案進行打分，最后將該方案所得的分數回傳到搜索樹中經過的所有節點，并計算更新每個節點的回報收益均值。這種過程持續執行成千上萬次，直到分配的方案分數能夠滿足要求或者搜索次數達到設定的數值為止。

3.2 實際應用

搜索運行過程中會面臨探索和利用這一對矛盾體[3]。探索是嘗試一些不同的和之前判定得分低的方案，從而增加發現更好方案的可能性。利用是指利用當前已知的情況實施策略，并把有限的采樣次數盡可能地用在評價高的方案上，從而驗證其有效性。

探索和利用是一對矛盾體，當計算總資源一定時，將更多的資源分配給當前表現優秀的方案就會忽略一些有潛力的方案，反之亦然。研究表明，在學習初期側重于探索后期側重于利用[3]具有不錯的效果。本文采用UCT算法[8]來計算每個節點的置信權重，如公式（9）所示。

4 系統優化

為了提高系統的計算效率、搜索準確性和泛化能力，需要對上述運行流程進行優化設計，以便更好地應對紛繁復雜的實際生產環境。

4.1 計算效率的優化

為了提高系統的整體運行效率，縮短得到滿意分配方案所花費的時間，采用了數據預存和并行計算兩個方法來提高計算速度。

1）數據預存

在計算過程中其實有大量的計算是重復性的。為了提高系統的計算效率，降低系統的計算復雜程度[11]，對一些計算過程量進行存儲保留，后續程序運行時可以從緩存區直接調取[11]，這樣可以大幅提高程序的運行速度。

2）并行計算

Python里對應這種計算密集型的任務可以采用多進程方式來實現[12-13]，涉及多進程的運行最關鍵的就是整個計算過程中探索的多樣性和共享數據的一致性。MCTS的幾種典型并行計算方式[14]分別為：葉子節點并行模式、多搜索樹并行模式、單搜索樹全局鎖并行模式、單搜索樹局部鎖并行模式。

本文采用的方式是不加鎖的蒙特卡洛樹搜索算法Lock-free MCTS[15]。在沒有保護的計算過程中有可能導致更新信息的丟失，但是在大規模的采樣環境和高效的單次搜索過程中這些影響很有限，可以被忽略[15]。

4.2 模型的搜索準確性優化

4.3 模型的泛化能力優化

1）應對航班時刻變化的能力

為了能更好地適應航線工作需求，提高模型應對復雜生產環境的能力，在計算過程中可以人為地為每個任務加入相對應的時間噪聲，如公式（7）和（8）所示。

2）應對突發事件的能力

在生產中會出現某個航班的非正常滯留（如目的地機場的天氣原因或航路的天氣原因等）和AOG（飛機故障）情況，這些情況的出現會打亂現有的人員分配計劃。如果出現類似情況，需要有對應的特殊處理方法，實際操作中的流程為：

a.從現有的航班管理系統或者生產人員那里了解航班的當前狀態；

b.鎖定已經處于工作中的人員分配方案；

c.更改非正常任務的工作時間范圍；

d.對還未進行工作的分配計劃進行清空；

e.對清空的計劃任務開始新的分配方案搜索；

f.用變化小但分數高的新方案來進行人員局部調整。

5 結束語

本文的主要工作是基于強化學習的蒙特卡洛樹搜索來完成任務的自動化分配。作為當前流行的機器學習方法在實際生產中的初步試探，取得了不錯的效果。目前系統信息環境比較局限，可以嘗試更加復雜多樣的信息環境，在多個信息維度下同時展開搜索。機器學習技術落地需要不斷的探索和嘗試，怎樣將這些前沿的研究成果轉化為實際生產力是我們應該不懈努力的方向。

參考文獻

[1] 吳軍.智能時代[M].北京：中信出版集團，2016：30-35.

[2] SILVER D，HUANG A，MADDISON C J.，et al. Mastering the Game of Go with Deep Neural Networks and Tree Search[J]. Nature，2016（1）：484-489.

[3] 馮超.強化學習精要核心算法與 Tensorflow實現[M].北京：電子工業出版社，2018：145-147，178-181，309-312.

[4] 郭憲，方勇純.深入淺出強化學習原理入門[M].北京：電子工業出版社，2018：18-22.

[5] 胡永宏，賀思輝.綜合評價方法[M].北京：科學出版社，2000：48.

[6] 吳軍.數學之美[M].北京：人民郵電出版社，2015：127-135，244-248.

[7] 陳瑞.針對大量業務數據的分析方法[J].航空維修與工程，2019（7）：52-56.

[8] BROWNE C.B.，POWLEY E.，WHITEHOUSE D，et al. A Survey of Monte Carlo Tree Search Methods[J]. IEEE Transactions on Computational Intelligence and AI in Games，2012（3）：1-43.

[9] AUER P. Finite-time Analysis of the Multiarmed Bandit Problem[J].Machine Learning，2002（47）：235-256.

[10] KOCSIS L，SZEPESV′ARI C. Bandit-based Monte-Carlo Planning[J].European Conference on Machine Learning，2006（9）：282-293.

[11] DOGLIO F. Mastering Python High Performance[M].陶俊杰，陳小莉，譯.北京：人民郵電出版社，2016：12-16，84-85.

[12] BEAZLEY D，JONES B K. Python Cookbook[M].陳舸，譯.北京：人民郵電出版社，2015：496-547.

[13] CHUN W. Core Python Applications Programming（3rd edition）[M].孫波翔，李斌，李晗，譯.北京：人民郵電出版社，2016：122-165.

[14] CHASLOT G，WINANDS M H.M.，HERIK H J V D. Parallel Monte-Carlo Tree Search[J].International Conference on Computers and Games，2008（9）：60-71.

[15] ENZENBERGER M，MULLER M.A Lock-free Multithreaded Monte-Carlo Tree Search Algorithm[J].Advances in Computer Games，2009（5）：14-20.

[16] NELLI F. Python Data Analyt- ics[M].杜春曉，譯.北京：人民郵電出版社，2016.

[17] MILOVANOVIC L. Python Data Visualization Cookbook[M].顓清山，譯.北京：人民郵電出版社，2016.

[18] 賈俊平，何曉群，金勇進.統計學（第六版）[M].北京：中國人民大學出版社，2016：57-58.

作者簡介

陳瑞，工程師，主要從事業務數據的分析與挖掘工作。