基于改進PSO-LSSVM模型的變壓器繞組熱點溫度預測

劉 闖，盧銀均，劉紅云，向 曉，王梁偉

（國網湖北省電力有限公司荊門供電公司，湖北 荊門 448000）

0 引言

變壓器是電力系統的核心設備之一，其安全穩定性是電網穩定運行的必要條件[1]。變壓器的使用壽命與其內部溫度及熱量散失密切相關。繞組熱點溫度是限制變壓器運行負載的主要因素，繞組溫度過高，會對變壓器的絕緣造成不可逆損害，嚴重影響變壓器的使用壽命[2]。因此，及時掌握變壓器繞組溫度變化情況，做好繞組熱點溫度預測工作，對保障電力系統穩定運行具有重要意義。

目前，國內外專家已對變壓器繞組熱點溫度進行了大量研究。國際上推薦的繞組熱點溫度計算公式來源于IEEEC57.91 和IEC354 導則[3]，但這些導則沒有考慮環境溫度的影響。隨著智能算法的興起，大量智能算法被應用到變壓器繞組熱點溫度預測領域。文獻[4]通過監測裝置獲取變壓器端部溫度、頂層、中層和底層油溫，建立了基于灰色神經網絡的變壓器繞組熱點溫度預測模型，取得了較好的預測效果，但預測模型的輸入量具有一定的局限性。文獻[5]采用Levenberg-Marquardt 算法對BP 神經網絡進行改進，建立了變壓器繞組熱點溫度預測模型，并采用實測數據對預測模型進行檢驗，結果表明，三層BP神經網絡的預測效果最好，但BP神經網絡易陷入局部最優解。文獻[6]根據實驗室模擬變壓器的實測數據，提取變壓器繞組熱點溫度預測模型的輸入量，采用遺傳算法（Genetic Algorithm，GA）優化支持向量機（Support Vector Machines，SVM）參數，建立了基于GA-SVM 的變壓器繞組熱點溫度預測模型，預測效果優于BP和Elman神經網絡，但預測精度有待提高。

針對上述變壓器繞組熱點溫度預測方法中存在的不足，本文在粒子群算法（Particle Swarm Opti?mization，PSO）基礎上，采用收縮因子對粒子速度更新方式進行改進，加強粒子在尋優過程中的搜索能力，提出了采用PSO 對最小二乘支持向量機（Least Squares Support Vector Machines，LSSVM）參數尋優的方法，建立變壓器繞組熱點溫度預測模型，并對該方法的預測效果進行驗證。

1 算法介紹

1.1 LSSVM算法

LSSVM是基于SVM的一種改進方法，它遵循結構風險最小化原則，其核函數的選擇與SVM 相同。二者的不同點在于，LSSVM采用平方項作為優化指標，并以等式約束代替SVM 的不等式約束[7]。LSS?VM 結構簡單，對小樣本非線性問題處理效果較好，在回歸、預測領域應用廣泛，LSSVM 回歸的原理及步驟可參考文獻[8]。

1.2 PSO算法

PSO 是一種基于群體搜索的智能算法，起源于飛鳥搜索食物，也就是利用個體間保持競爭又相互合作，在復雜的空間中找到最優解。因其具有簡單、容易實現且需要調節的參數少等優點，常被用于回歸算法的參數尋優[9]。

假設D 維空間存在種群X=( x1,x2,…,xn)，該種群包含n 個粒子。將其中的第i 個粒子看做是D 維空間中的一個向量Xi=[ xi1,xi2,…,xil]T，即在D 維空間中第i 個粒子的位置。根據目標函數計算D 維空間中各粒子位置Xi的適應度值。第i個粒子速度的向量為Vi=[vi1,vi2,…,vil]T，個體極值的向量為Pi=[ pi1,pi2,…,pil]T，群 體 極 值 的 向 量 為 Pg=[ pg1,pg2,…,pgl]T。兩個極值通過迭代更新粒子的速度和位置，即：

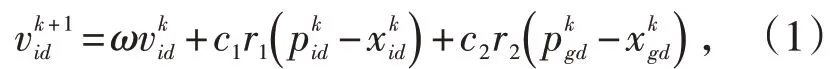
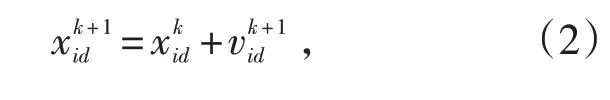
式中，d=1,2,…,D；i=1,2,…,n；k為當前迭代次數；vid為當前速度；c1、c2為加速因子，且c1、c2均大于0；ω為慣性權重；r1和r2為隨機函數，取值區間為[0,1]；和為D 維上第i 個粒子在k+1 次迭代的位置和速度。

PSO 算法在搜索過程中過度依賴Pbest和gbest，搜索能力有限。本文提出在PSO 算法中引入收縮因子，收縮因子的變化既能保證PSO算法的收斂性，又不受速度邊界的影響，加快種群全局搜索的同時又能增強粒子的局部搜索能力[10-11]。速度更新公式為：

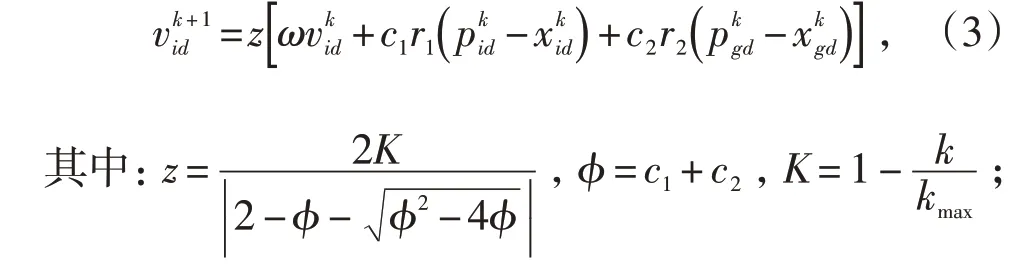
式中：z為收縮因子；φ為總加速因子；kmax為總迭代次數。K 為收縮系數，用來控制PSO 的全局和局部搜索能力；當其趨近1 時，會造成大量的全局搜索行為，導致PSO 算法收斂慢；當其趨近0 時，大量的局部搜索導致收斂過快。

仿真分析證明，在對多維函數進行優化時，引入收縮因子的PSO算法在初始階段具有良好的全局搜索能力，而后期局部尋優能力增強，收斂性能良好，因此被廣泛應用。

2 改進PSO-LSSVM預測模型

研究表明，LSSVM 算法適合小樣本回歸，具有較高的預測精度，但預測效果受懲罰因子C 和核函數參數σ的影響，當C 和σ取值不當時，容易出現欠學習或過學習現象，均不利于樣本回歸。因此有必要采用尋優能力更強的改進粒子群算法及LSSVM的最佳參數組合。本文基于改進PSO-LSSVM 預測模型進行建模，流程如圖1所示。具體步驟如下。

（1）對變壓器繞組熱點溫度樣本進行預處理，樣本數據由不同類別的數據組成，且單位均不相同，若直接建模，通過特征向量內積計算的特征值過大，本文采用公式（15）對樣本數據進行歸一化：

式中：Ti、Tmax、Tmin分別為變壓器繞組熱點溫度樣本數據的原始值、最大值和最小值；Ti′為變壓器繞組熱點溫度歸一化后的輸入值。

圖1 改進PSO-LSSVM預測模型建模流程

（2）初始化設置LSSVM的核函數參數，令懲罰因子C=100，核函數寬度σ2=2.5。經預測模型運算后輸出結果，然后根據式（16）計算適應度值I：

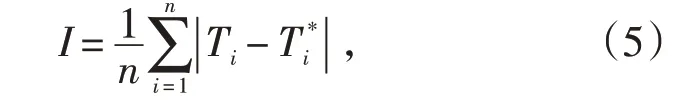
式中：n為樣本容量；Ti*為變壓器繞組熱點溫度預測值。

（3）設置改進PSO 參數，種群規模d=30，加速因子c1=c2=2.05，總迭代次數kmax=300，采用線性遞減的方法將慣性權重ω從0.9遞減到0.4。

（4）將懲罰參數C 和核函數參數σ作為粒子，初始值分別為C=100、σ2=2.5，將其記作當前個體最優解，并計算初始適應度值，搜索適應度值的最優解作為當前全局最優適應度值，與其對應的粒子即為全局最優解。

（5）迭代過程開始，根據公式（2）和（3）計算粒子新的速度及位置。

（6）將新的速度和位置作為核函數和懲罰因子重新帶入LSSVM模型進行訓練輸出，計算新適應度值。

（7）比較步驟（6）中的新適應度值和當前適應度值，如果新適應度值優于當前適應度值，則更新適應度值，并將新適應度值對應的粒子值更新為個體最優值。

（8）如果新適應度值比全局適應度值更優，則將其更新為全局適應度值，并將與新適應度值相對應的速度和位置更新為全局最優解。

（9）判斷迭代后的結果能否滿足尋優及迭代次數的要求，若是則結束計算，輸出全局最優解；不滿足則返回步驟（5）。

（10）將尋優后的C和σ帶入LSSVM模型，即可進行變壓器繞組熱點溫度預測。

2 算例分析

本文采用文獻[11]中的100 組實驗數據組成樣本進行算例分析。在連續時間序列上取100組實驗數據，時間間隔為30 min，數據包括變壓器負載電流、頂層油溫、底層油溫、油箱上死角、油箱下死角溫度及環境溫度，將100組數據依次編號為1—100，部分實驗數據如表1所示。

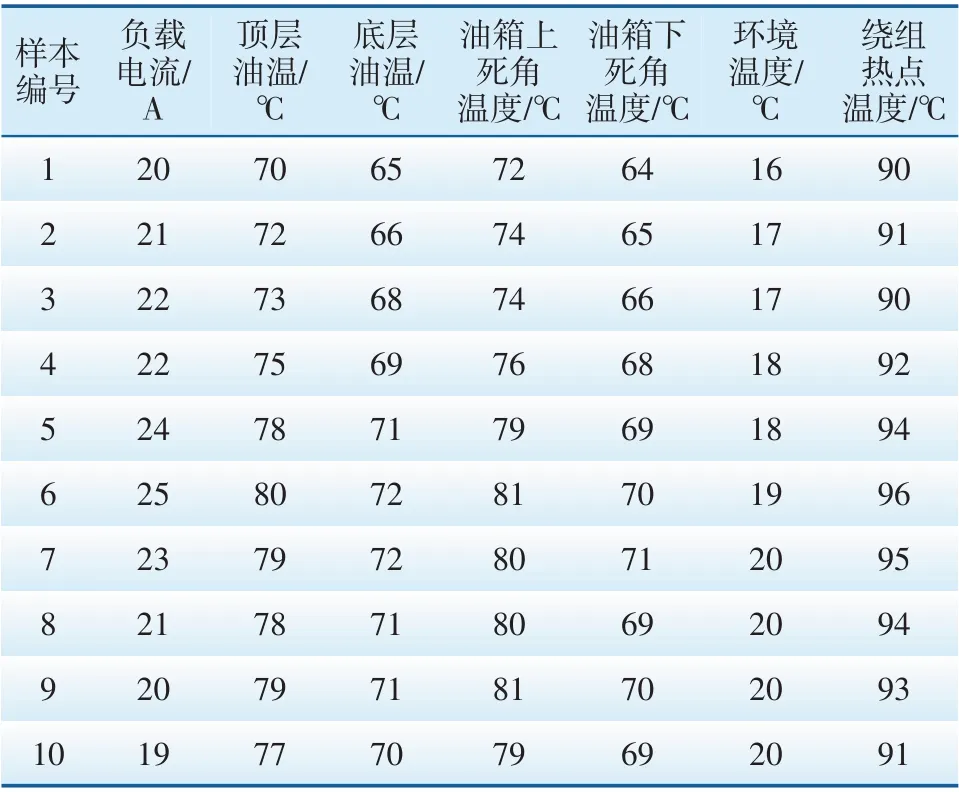
表1 部分實驗數據

在Matlab軟件中進行仿真，將負載電流、頂層油溫、底層油溫、油箱上死角溫度、油箱下死角溫度及環境溫度作為變壓器繞組熱點溫度預測模型的支持向量，100組樣本數據分為兩部分，前90組數據為訓練集，后10 組為測試集，分別采用改進PSO 算法和PSO 算法訓練測試集數據，對LSSVM 參數尋優。改進PSO算法獲得的最優參數為C=58.36、σ2=3.25，PSO 算法獲得的最優參數為C=65.84、σ2=3.76，兩種算法的適應度曲線如圖2所示。

從圖2中可知，PSO-LSSVM模型大約迭代計算180次才能找到全局最優解，而改進PSO-LSSVM模型只需約80次即可完成迭代。由此可見，改進PSO算法能夠明顯加快收斂速度。

將最優參數分別賦與LSSVM 變壓器繞組熱點溫度預測模型，對后10 組測試集數據進行預測，預測結果如圖3 所示。由圖3 可知，改進PSO-LSSVM模型預測效果更好。

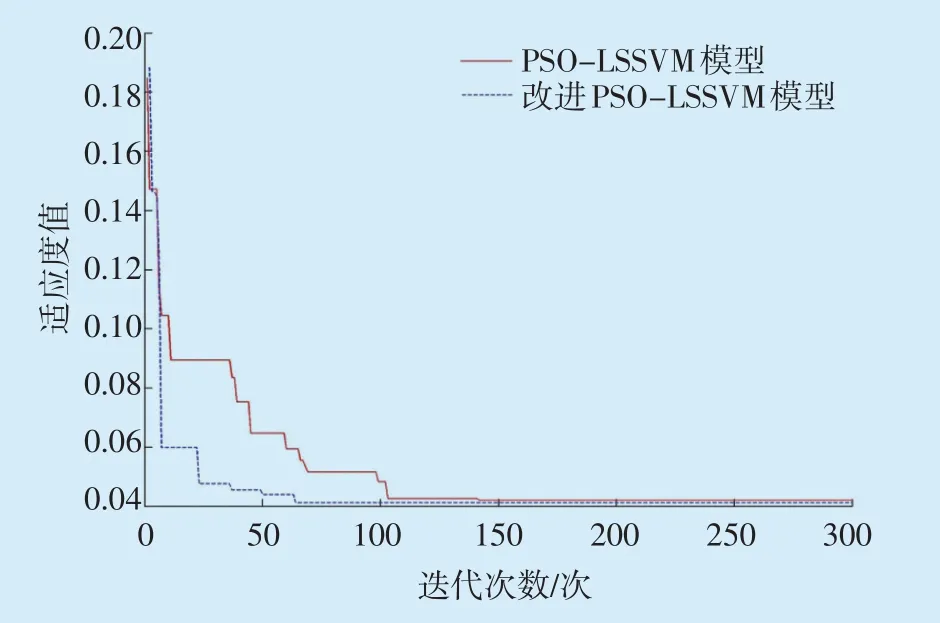
圖2 兩種模型的適應度曲線

圖3 測試集數據預測結果

為檢驗預測模型的精度，采用平均相對誤差對本文提出的變壓器繞組熱點溫度預測方法進行評價，平均相對誤差計算公式如下：

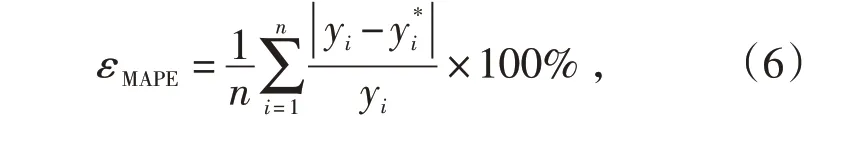
式中：n 為測試樣本的數量，yi為第i 個實際值，為第i個預測值。

為進一步驗證本方法的正確性，采用100 組樣本數據另外建立GA-SVM 預測模型和GA-BP 預測模型，通過測試集數據檢驗各種預測模型的精度，4種預測模型的平均相對誤差如表2所示。由表2可知，改進PSO-LSSVM 模型的平均相對誤差最小，收斂時間最短。可見基于改進PSO-LSSVM 的變壓器繞組熱點溫度預測方法明顯優于其他方法。

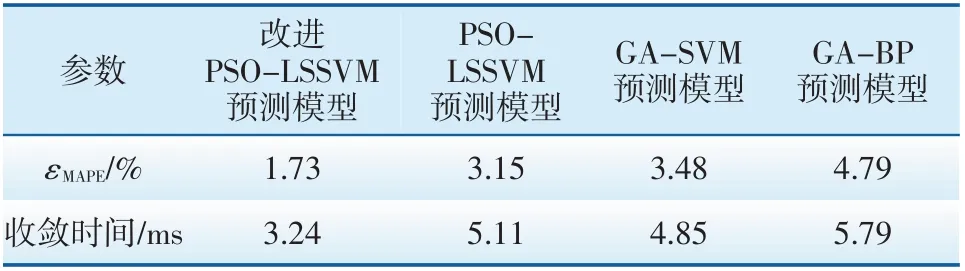
表2 4種模型預測誤差

3 結束語

本文針對粒子群算法存在收斂速度慢、尋優能力差等不足，采用收縮因子對粒子群算法進行改進，建立了基于改進PSO-LSSVM 的變壓器繞組熱點溫度預測模型，取得了理想的預測效果，驗證了該方法的正確性。變壓器繞組熱點溫度變化過程較復雜，本文收集的樣本數據有限，未來將開展相關實驗，獲取更多樣本數據，進一步完善預測模型。