多源數據對林分動態預測的影響及不確定性分析*

田相林 廖梓延 孫帥超 薛海連 王 彬 曹田健

1.西北農林科技大學林學院 生態仿真優化實驗室 楊凌 712100； 2.赫爾辛基大學林學系 赫爾辛基 FI-00014； 3.中國科學院成都生物研究所 成都 610041； 4.中國科學院大學 北京 100039； 5.福建農林大學 福州 350002； 6.西北農林科技大學理學院 楊凌 712100； 7.青海大學農林科學院 西寧 810016)

在森林立地、密度效應、林分生長以及經營措施等方面的理論研究中，森林建模往往要求林分觀測數據是一種控制試驗的產物，并假定試驗是被設計在嚴格可控的環境中以檢驗特定變量對林分生長動態的影響。然而，受限于控制森林生態系統環境的能力、調查所能承擔的時間和空間范圍以及觀測到特定變量的能力等，森林動態預測研究通常依賴于有限數量并伴隨復雜誤差結構的數據，使得經典統計模型的假設情境往往難以被滿足(Clark， 2007)。在森林生態系統研究中，林分生長收獲分析需要綜合多種數據類型，如臨時樣地、固定樣地、解析木和生長錐木芯等，這些信息由于采用不同抽樣設計或觀測方法等原因常常具有極其復雜的誤差結構特征，且其復雜程度會隨不同時期或類型的新數據加入而不斷累積。同時，在林分動態預測與生長收獲模型應用研究中，來自非控制條件下部分觀測過程的信息往往需要作為統計推斷的基礎(Dietze， 2017)，諸多不可控的環境或機制因素都會導致森林調查數據與林分動態預測之間形成復雜的信息交互體系，最終使得模擬與預測的可靠性無法被量化評價。

隨著生態系統探討問題的復雜性不斷升高，現代模擬和計算技術被廣泛應用于相關領域研究中，其中，貝葉斯框架的潛在假設使得貝葉斯方法不再受模型數據量和控制條件等因素制約，且具備綜合多源數據信息的能力(Clarketal.， 2007)，其應用在20世紀90年代后飛速發展(Gelfandetal.， 1990； Berger， 2000)，并逐漸被林業研究者所關注(Greenetal.， 1996； Bullocketal.， 2007； Clarketal.， 2007； Metcalfetal.， 2009)。貝葉斯估計值同時依賴于先驗和后驗分布，復雜問題的后驗信息往往由迭代數據隨機取樣來確定，即產生參數的完整后驗分布，這意味著許多統計值可從生成的樣本中獲得。盡管經典的最大似然方法和貝葉斯方法會產生相似的參數估計(Lietal.， 2011)，但貝葉斯方法不需要像最大似然方法那樣的附加條件和特定的分布假設，貝葉斯框架下林分模型的構建，可極大限度減小統計學假設對數據的限制，并能對模型本身和林分生長的不確定性進行合理量化分析(Hartigetal.， 2012)。基于Tylor展開式或Monte Carlo抽樣方法推斷或預測的不確定性可以解析為不同的來源，包括數據的不確定性、模型結構的不確定性和模型參數的不確定性，進而對不確定的傳遞過程進行量化(Lebaueretal.， 2013； Dietze， 2017)，其中多維相關性基礎上的參數不確定性是生態系統模型開發與應用中難以回避的內容(Van Oijen, 2017)。

在森林動態預測研究中，貝葉斯方法也逐步得以應用，如地上生物量模型(Zapata-Cuartasetal.， 2012； Zhangetal.， 2013)、直徑分布模型(Bullocketal.， 2007)和直徑生長模型(Clarketal.， 2007)等。貝葉斯方法的核心優勢在于其對數據與模型關系的描述，如估計多層次/體系模型(Gelmanetal.， 2007； Dietzeetal.， 2008)、利用有限數據信息校正復雜模型(Van Oijenetal.， 2005)、從不同模型中合并預測值(Radtkeetal.， 2006)以及克服數據稀疏問題(Metcalfetal.， 2009)等，而目前森林建模研究中，貝葉斯框架下數據與模型間信息融合與復雜誤差結構的討論往往集中于過程機制模型而非經驗模型(Hartigetal.， 2012； Dietze, 2017； Van Oijen， 2017)。森林生長收獲經驗模型的主流仍然是基于系統性設計的長期觀測(Pretzsch， 2010)，并對數據的誤差體系有著詳盡考量(Kangasetal.， 2006)； 然而這種大量建模數據的需求，在國內多數林區難以滿足。由于缺少系統性的長期觀測，且數據誤差隨不同抽樣策略或數據源而劇烈波動，使得經典回歸分析理論中的許多假設并不成立，因此將誤差結構納入模型體系尤為重要(唐守正等， 1995； 1998； 符利勇等， 2014)。

從森林生長收獲模型的尺度上來說，全林模型只需要相對較少的信息來模擬林分生長。相比徑階和單木模型，全林模型所模擬的基本單元是林分和立地參數，包括年齡、林分斷面積、立地指數和蓄積量等，雖然無法像徑階或單木模型一樣分析林分結構的動態變化，但全林模型可以保證較為準確的未來林分蓄積生長狀況信息，這在森林經營實踐中非常重要(Weiskitteletal.， 2011)。可變密度全林模型將林分密度作為繼林分年齡、立地質量的第3個變量，可以描述特定樹種和立地條件下任意林分的生長，在密度控制和森林經營規劃中有著廣泛應用(張少昂， 1986； 李希菲等， 1988； 唐守正， 1991； 1993； 1999； 洪玲霞， 1993； 洪玲霞等， 2012； Weiskitteletal.， 2011)。

本研究以數據信息要求較低、應用廣泛的可變密度全林模型為例，采用貝葉斯數據-模型框架，構建森林資源連續調查中數據信息融合與模型學習的關系，探究隨著新一期數據不斷加入，模型參數概率分布和模型預測結果的變化規律； 在考慮誤差分布和異方差等特征的基礎上，比較角規臨時樣地、矩形固定樣地、樹干解析3種數據類型對模型構建和林分動態模擬的影響，以提高模型預測的準確性和可靠性； 同時，基于不確定性的量化評估，為森林調查中的數據收集策略提供建議。

1 數據與方法

1.1 數據

模型開發數據源自陜西省寧陜縣火地塘林區(108°21′—108°39′E，33°18′—33°28′N)和旬陽壩林區(103°58′—109°48′E，32°29′—33°13′N)。數據采集海拔范圍為1 200～1 800 m，坡度范圍為15°～42°。土壤為森林棕壤，平均厚度50 cm。該區域屬亞熱帶濕潤山地氣候，年均氣溫8～12 ℃，年均降雨量1 100 mm。這2個林區原始天然林于20世紀60—70年代進行過采伐，目前多為天然次生林或人工林。研究區樣地位置分布見圖1。

研究共使用215塊角規繞測臨時樣地、22塊20 m×20 m矩形固定樣地和11株中等木解析木，所有樣地均為油松(Pinustabulaeformis)純林(油松斷面積占比高于90%)或相對純林(油松斷面積占比65%～90%)。角規斷面積系數為1 m2·hm-2。角規繞測臨時樣地調查數據包括1990年森林經理調查(李悅黎等， 1993)獲得的58塊油松相對純林樣地和2005年森林經理調查獲得的68塊油松相對純林樣地。為減少抽樣設計帶來的誤差，采用完全相同的方法于2012年補充調查45塊油松樣地，最終獲得3期角規樣地調查數據(表1)。除了角規繞測臨時樣地以外的 22塊矩形固定樣地和11株油松中等木樹干解析數據，被用于比較不同數據類型對模型表現的影響，全部數據對比見表2。

本研究多源數據包括森林生長收獲建模中2種常見的數據狀況： 一為相同抽樣設計下不同時期的調查數據(表1)，數據誤差結構不同多為設備、人員和質量控制差異造成； 二為不同抽樣設計本身導致誤差的系統性差異，即本研究中點抽樣的臨時樣地、每木檢尺的矩形固定樣地、解析木(表2)在抽樣和林分調查因子測算原理上存在系統性區別。

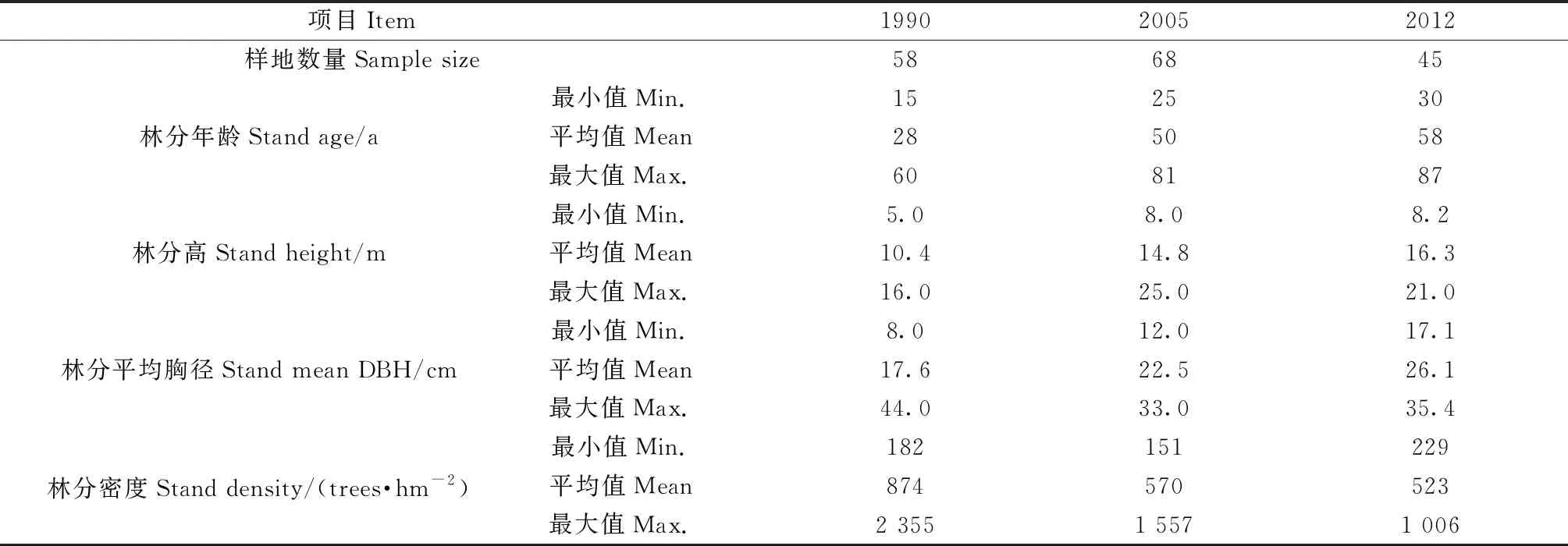
表1 用于模型循環更新測試的3期角規樣地調查數據

表2 模型構建中比較的3種數據類型

1.2 可變密度全林模型

可變密度全林模型僅需對基礎林分調查信息進行參數化，可用于模擬給定林分的平均高H(m)、斷面積G(m2·hm-2)、平均胸徑D(cm)等。模型體系如下：

(1)

(2)

(3)

(4)

(5)

(6)

(7)

根據油松生長曲線和數據中的樹高變動系數，設置A0=30 年(吳恒等， 2015)。通過調整SDI和SCI，可模擬不同林分密度和立地質量的林分生長過程。整個模型體系不依賴于固定樣地的連續復測，林分密度變化由斷面積與平均胸徑的關系獲得。

關于本林區不同數據集和指標對立地評價的具體影響以往研究已進行了詳盡探討(吳恒等， 2015； 郭小陽等， 2017)，本研究之所以采用給定年齡下的林分平均高期望值，即地位級指數用于林分立地質量評估，是因為1990和2005年的調查數據中許多樣地缺少優勢木記錄，無法構建常規立地指數曲線。林分平均高導向曲線、林分總斷面積模型和平均胸徑模型均采用Schumacher模型(Schumacher， 1939)的基本結構。樹高模型擬合同時測試臨時樣地、固定樣地、解析木3種數據類型，胸徑和斷面積模型僅比較臨時樣地和固定樣地2種數據類型。林分密度指數推算基于完滿立木度林分密度(N)與平均胸徑(D)的關系，即需要完滿立木度林分數據，采用逐步剔除(李希菲等， 1988)對樣地進行篩選： 1) 利用全部數據擬合Reineke(1933)方程lnN= α-βlnD； 2) 舍棄所有低于該方程回歸線的低密度林分，并用剩余數據繼續擬合該方程； 3) 舍棄低于新回歸線的所有樣地。剩余樣地假定其為完滿立木度并重新擬合該方程，最終獲得式(1)中的參數β。分別完成地位級指數和林分密度指數模型擬合后，各樣地SCI和SDI通過計算得到，進而依次完成林分斷面積和胸徑模型擬合。方程組聯立求解參數依1.4節操作。

1.3 貝葉斯數據-模型框架

貝葉斯方法提供數據信息融合與模型學習框架，新的數據信息可不斷加入模型中，該過程可以簡單地表述為：

p(θ|D)∝p(D|θ)×p(θ)。

(8)

式中：p(θ|D)和p(θ)分別為模型參數θ的后驗和先驗分布；p(D|θ)為似然函數，即給定參數θ時數據D被觀測到的概率。

對于過程機制模型，先驗分布通常基于生理學觀測數據或理論推測的范圍(Van Oijenetal.， 2005)。對于參數數量較少且沒有生理學含義的經驗模型，在首次校正(參數擬合)時，采取無信息先驗方式，參數聯合后驗分布取決于似然函數，而之后的數據融合與模型更新過程中，將前一次擬合得到的參數聯合后驗分布作為新數據加入時的先驗。本研究中參數聯合后驗分布不可解析，采用多維核密度估計方法得到近似分布，作為重新校正過程中的先驗。

由于多種數據類型被應用于貝葉斯校正過程，不同數據類型觀測誤差不同，因此需要對似然函數進行分解。如對于樹高導向曲線[式(2)]，似然函數被分解為：

p(θ|D)∝p(DTP|θ)×p(DPP|θ)×

p(DSA|θ)×p(θ)。

(9)

式中：DTP、DPP和DSA分別表示角規臨時樣地(temporary plot，TP)、矩形固定樣地(permanent plot，PP)和解析木(stem analysis，SA)中的觀測數據，此時的p(θ|D)表示綜合考慮多種數據類型(multi-type/multi-source data)的參數后驗概率。

考慮到林分調查中觀測誤差的不穩定性，同時異常值很難有明確的判別標準，本研究采用重尾正態分布概率密度函數描述誤差容易受異常值影響而導致有偏的估計(Siviaetal.， 2006)：

(10)

式中：σi為噪聲尺度因子，用于描述第i次觀測隨機誤差的不確定性；Ri為第i次觀測值與對應模型預測值的離差除以σi。

林業調查數據的另外一個重要特征就是異方差，即觀測值偏離均值的程度會受其他因素影響而非恒定。這種異方差特征一方面違反大部分經典統計學假設，另一方面也導致模型預測中錯誤的置信域估計。角規臨時樣地、矩形樣地和樹干解析信息需要依據噪聲尺度因子σi進行融合，對于每種數據類型的每個響應變量，均需要分別擬合其誤差分布。本研究假定觀測誤差的異方差性質為：

(11)

1.4 聯立方程組估計下的參數聯合后驗概率密度

可變密度全林模型理論上應按1.2節介紹以特定順序單獨擬合，然而，由于全林模型內各預估模型經常會同時作為一個整體被使用，故本研究采用聯立方程組形式構建模型，這就需要對似然函數進行調整。以1990年采集的角規臨時樣地數據擬合式(5)斷面積預測模型為例，在方程式單獨擬合時，其參數后驗概率密度為：

p(c1,c2,c3,c4,gG,hG)。

(12)

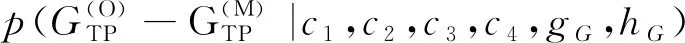
p(α,β,b1,b2,c1,c2,c3,c4,d1,d2,d3,d4,glnN,hlnN,gH,

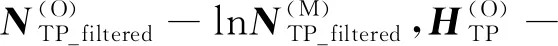
(13)

1.5 參數估計方法、收斂診斷與不確定性評估

由于參數聯合后驗概率分布不可解析，故本研究采用集成Metropolis-Hastings算法的Markov Chain Monte Carlo(MCMC)技術(Hastings， 1970； Metropolisetal.， 1953)模擬計算參數分布，并運用Gelman-Rubin收斂診斷技術(Brooksetal.， 1998； Gelmanetal.， 1992)確保MCMC收斂至正確的后驗分布，該方法的優勢在于整個過程既不涉及共軛計算，也不涉及條件概率和聯合后驗分布解析式的推導計算(Van Oijenetal.， 2005)。參數聯合后驗概率分布由MCMC的105次迭代生成，由于MCMC在開始階段未收斂至后驗分布，故將鏈的前10%作為“燒入”(burn in)舍棄掉(Gilksetal.， 1996)。平行運行3條MCMC鏈，計算其MPSRF(multivariate potential scale reduction factor)，該值較低時，代表不同起始值的子鏈最終獨立收斂至相同的后驗分布。本研究設定MPSRF接受閾值為1.05，是一種相對嚴格的收斂診斷標準(Brooksetal.， 1998)。

不確定性評估采用Monte Carlo抽樣方法進行計算。試驗中截取MCMC記錄的后1/2，每隔10條記錄抽取1組參數，每條子鏈得到5 000組參數值，3條子鏈共計15 000組參數值。盡管參數聯合后驗概率分布無法被解析，但無論是參數的邊際分布、相關性矩陣、標準差等信息，還是預測的貝葉斯可信區間，諸多不確定性指標均可直接通過該樣本計算獲得。后續計算采用多維核密度估計方法得到近似分布，作為重新校正過程中的先驗，該過程通過R工具包“BayesianTools”實現(Hartigetal.， 2019)。

采用Sobol指數量化分解各參數不確定性對最終預測不確定性的貢獻(Caribonietal.， 2007； Saltellietal.， 2008)。該方法可將不確定性分解到任意參數組，通過考慮參數相關性后單個參數所貢獻的總效應(STi)對不確定性傳遞過程進行評價，相應計算公式為：

(14)

式中：x-i表示給定除xi以外的所有模型參數；Y表示模型輸出變量。

基于Monte Carlo輸出結果可用于計算上述指標(Ioossetal.， 2020)。

各數據集本身規模不同，本研究采用自舉法分析數據規模對模型預測不確定性的影響。選取臨時樣地這一數據集，因為數據集涵蓋林分條件，更為多樣化。依次設置樣本數量N的規模為10、20、30、…、200塊樣地，進行以下計算： 1) 有放回的重抽樣，樣本數量為N； 2) 基于抽取到的樣地數據對模型參數進行擬合，采用擬合結果進行預測； 3) 重復1、2過程1 000次。

2 結果與分析

2.1 不同時期調查信息的動態融合

區別于經典回歸參數符合正態分布的假設，本研究貝葉斯方法獲得的參數分布是不可解析的。盡管參數后驗分布并不嚴格對稱，但除個別參數呈明顯偏態分布外，整體而言均值與最大后驗概率估計值(maximum a posterior estimates,MAP)相差極小(表3、4)。圖2以參數b1為例，展示了隨著新數據加入參數邊際分布不斷更新的過程。樹高生長的上漸近線參數b1(樹高生長極大值)隨著新數據加入不斷升高，不確定性逐步降低；同時，參數b1與b2存在較高相關性，且其聯合分布表現出明顯正向關聯(圖3)，隨著數據更新，聯合分布峰值逐漸升高，參數不確定性也隨之下降。

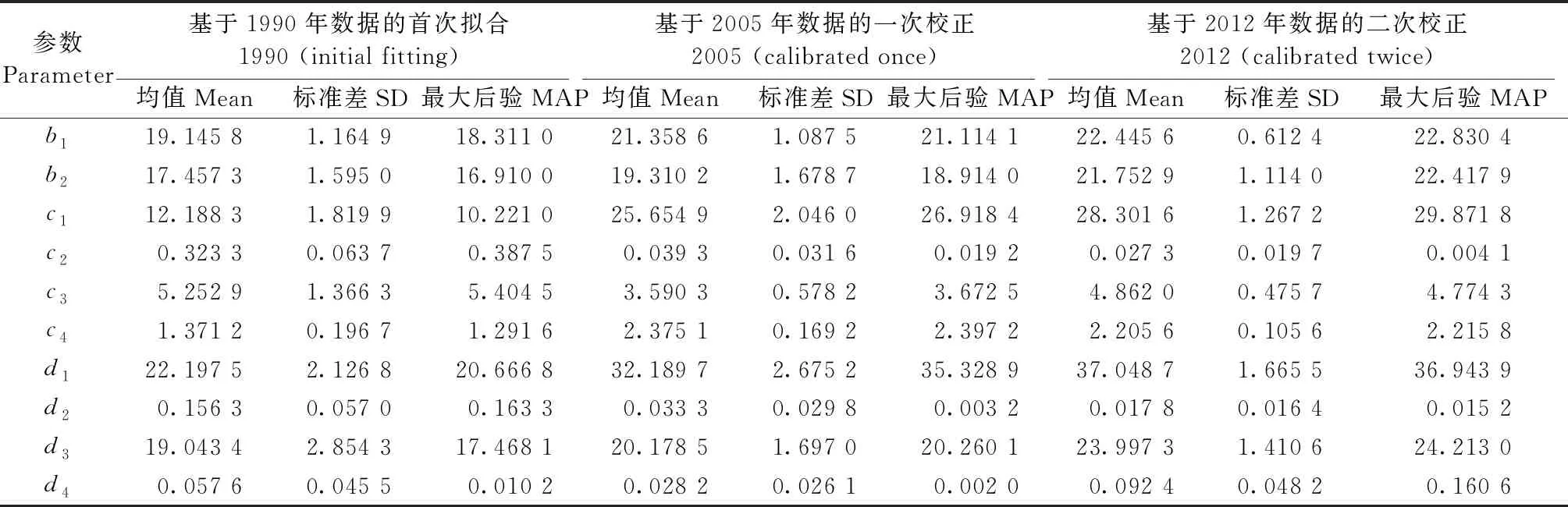
表3 參數循環更新過程中后驗概率密度分布的變化①

表4 基于多源數據的參數后驗概率分布

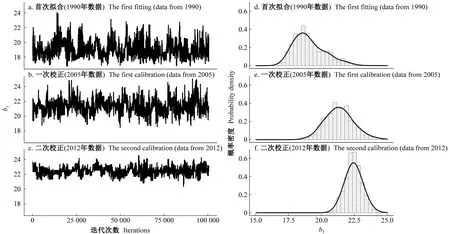
圖2 馬爾科夫蒙特卡洛迭代及參數b1后驗概率密度的變化過程

圖3 循環更新中參數b1與b2的聯合后驗概率分布

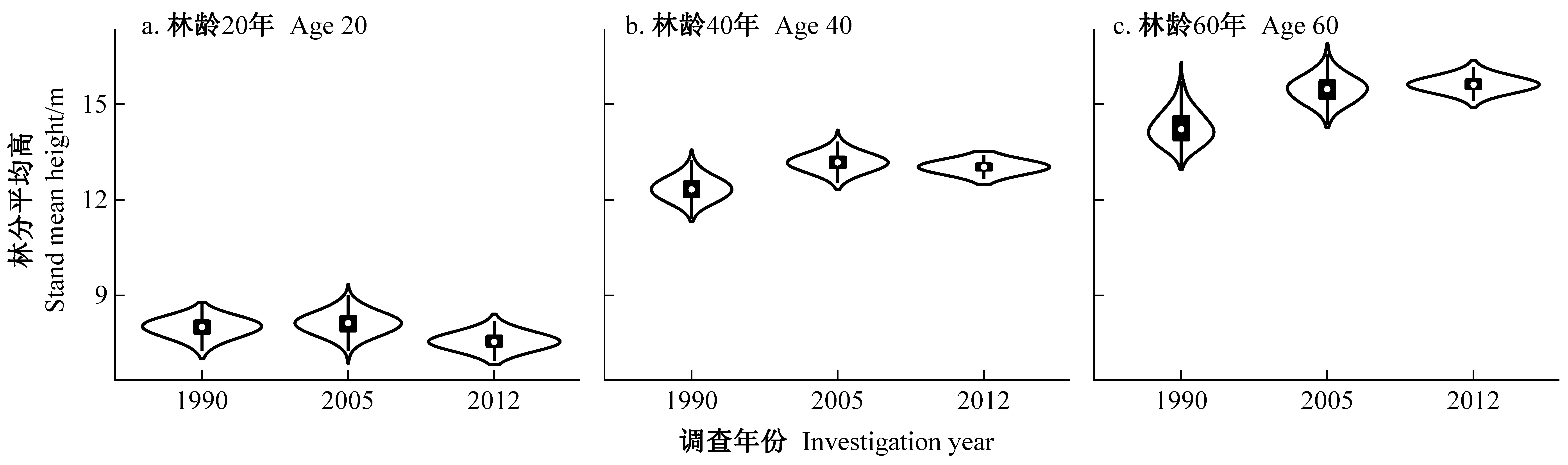
圖4 林分平均高導向曲線在20、40、60年時的樹高預測分布

隨著參數概率分布改變，模型預測結果也隨著新數據加入不斷變化。貝葉斯框架下，參數不確定性最終會對預測的不確定性產生影響。基于1990年數據擬合模型預測的不確定性高于之后2次校正得到的模型(圖4、5)。對于95%貝葉斯可信區間而言，基于1990年數據擬合的模型整個預測周期內樹高導向曲線的平均不確定區間為2.3 m(圖5a)，經2005年數據一次校正后不確定性下降至1.9 m(圖5b)，而經2012年數據二次校正后不確定性下降至1.1 m(圖5c)。同時，首次參數化時的模型在20年樹高導向曲線估計中傾向于給出更高的幼齡林樹高預測(圖4a)和更低的成過熟林樹高預測(圖4c)。

林分動態預測過程中，數據與模型的關系是相輔相成的： 一方面，模型的開發和參數化需要基于數據； 另一方面，模型的表現也可直接反映數據特征信息。在數據信息融合與模型學習關系構建時，模型預測的最大概率曲線在幼齡林和成過熟林模擬上不斷進行細微調整(圖5)，模型對數據信息的不斷吸收，更顯著的作用是不斷更新模型預測的不確定性。基于1990年數據進行模型擬合后，林分平均高、斷面積和平均胸徑的預測不確定性區間均在25～30年最低，而在其他年齡階段的不確定性則相對更高(圖5a、5d、5g)。經2005和2012年數據校正后，各齡階的不確定性預測逐漸平衡。以林分平均胸徑預測為例， 1990年數據對應最低不確定性出現在林齡25年(圖5d)，經2005年數據一次校正，最低不確定性出現在林齡34年(圖5e)，而經2012年數據二次校正，最低不確定性出現在林齡48年(圖5f)。

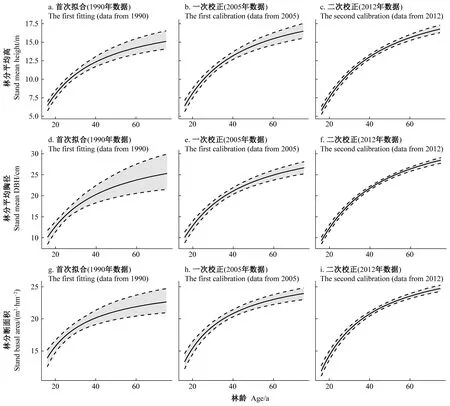
圖5 林分平均高(導向曲線)、平均胸徑和斷面積預測的更新變化過程(SCI=11, SDI=600)

2.2 不同數據類型對林分模擬的影響

角規繞測臨時樣地、矩形固定樣地、解析木數據在抽樣原理、測量誤差等方面的區別，導致模型參數擬合也存在差異。綜合多種數據類型的模型校正基于多個似然函數相乘來描述數據與模型的關系，即同時考慮數據量和數據準確性對似然的影響。參數估計時，對于不同數據集中觀測誤差大小、變異幅度及其方差異質性的假設，會基于模型與數據的匹配程度進行自動調整，因此并不需要預設各數據集在總體似然函數中所占比重。單從邊際分布考慮，綜合多源數據的模型參數大多是對角規臨時樣地、固定樣地和解析木對應模型參數的折中平均，且整體上與角規臨時樣地的擬合結果最為接近(圖6e、6h)。相比樣地調查，解析木數據傾向于給出更高的參數b1估計，即更大的樹高極大值(圖6g)。從聯合后驗分布角度來看，樣地調查數據給出的參數估計比解析木參數有著更強烈的相關性(圖7)。在樹高導向曲線擬合中，林齡20年時幾種類型數據給出的預測結果是相似的(圖8a)，林齡40年(圖8b)和60年(圖8c)時基于解析木的預測則明顯高于其他數據組。

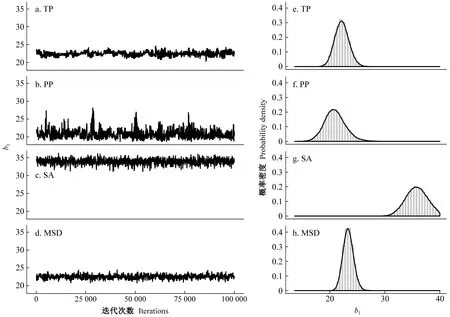
圖6 不同數據類型中馬爾科夫蒙特卡洛迭代及參數b1后驗概率密度的變化過程

相比之下，基于多源數據構造的全林模型，在林分平均高、平均胸徑和斷面積預測中均表現出最低不確定性。固定樣地數量遠低于臨時樣地，調查年份均為2012—2015年，且多為坡度較緩的林分，這使得其在林分斷面積生長預測和不確定性估計上與臨時樣地明顯不同。基于固定樣地的預測結果表明，林分斷面積增長在林齡35年后并不會大幅減緩(圖9e)，但這種預測也伴隨著極高不確定性(±30.1%)。各參數對模型預測不確定性的貢獻并不相同，斷面積預測模型參數c4與胸徑預測模型參數d4在式(5)和式(6)中傳遞的不確定性明顯低于其他相關參數(表5)。同時，由于參數聯合后驗概率分布中參數相關性較高，各參數Sobol總效應指數加和后的數值也會遠高于1。

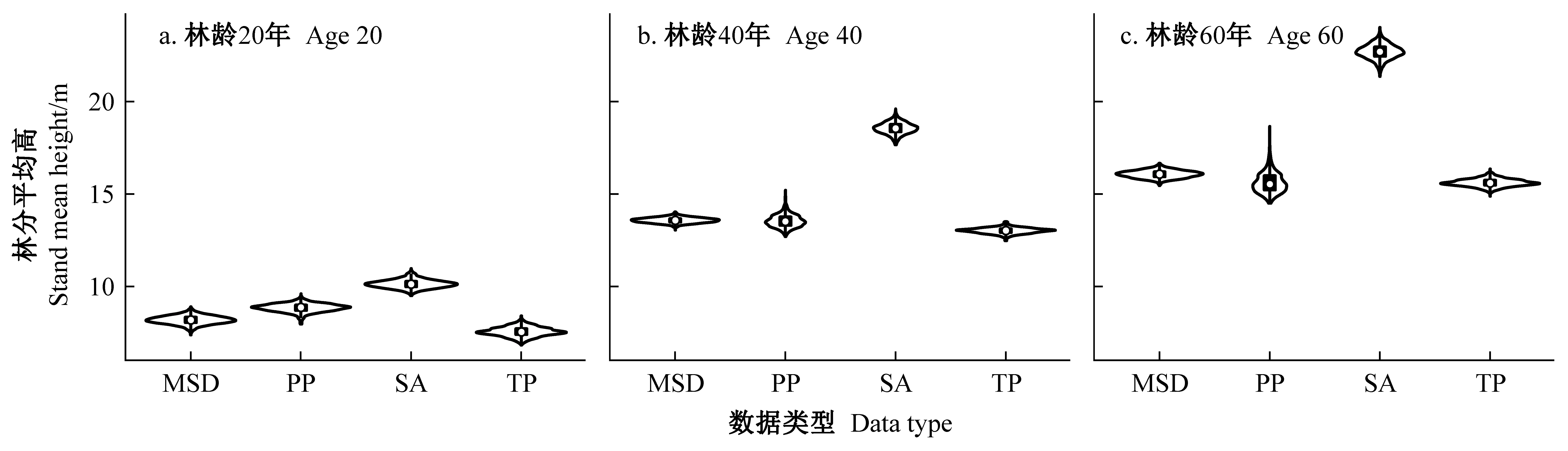
圖8 基于不同數據類型林分平均高導向曲線在20、40、60年時的樹高預測分布

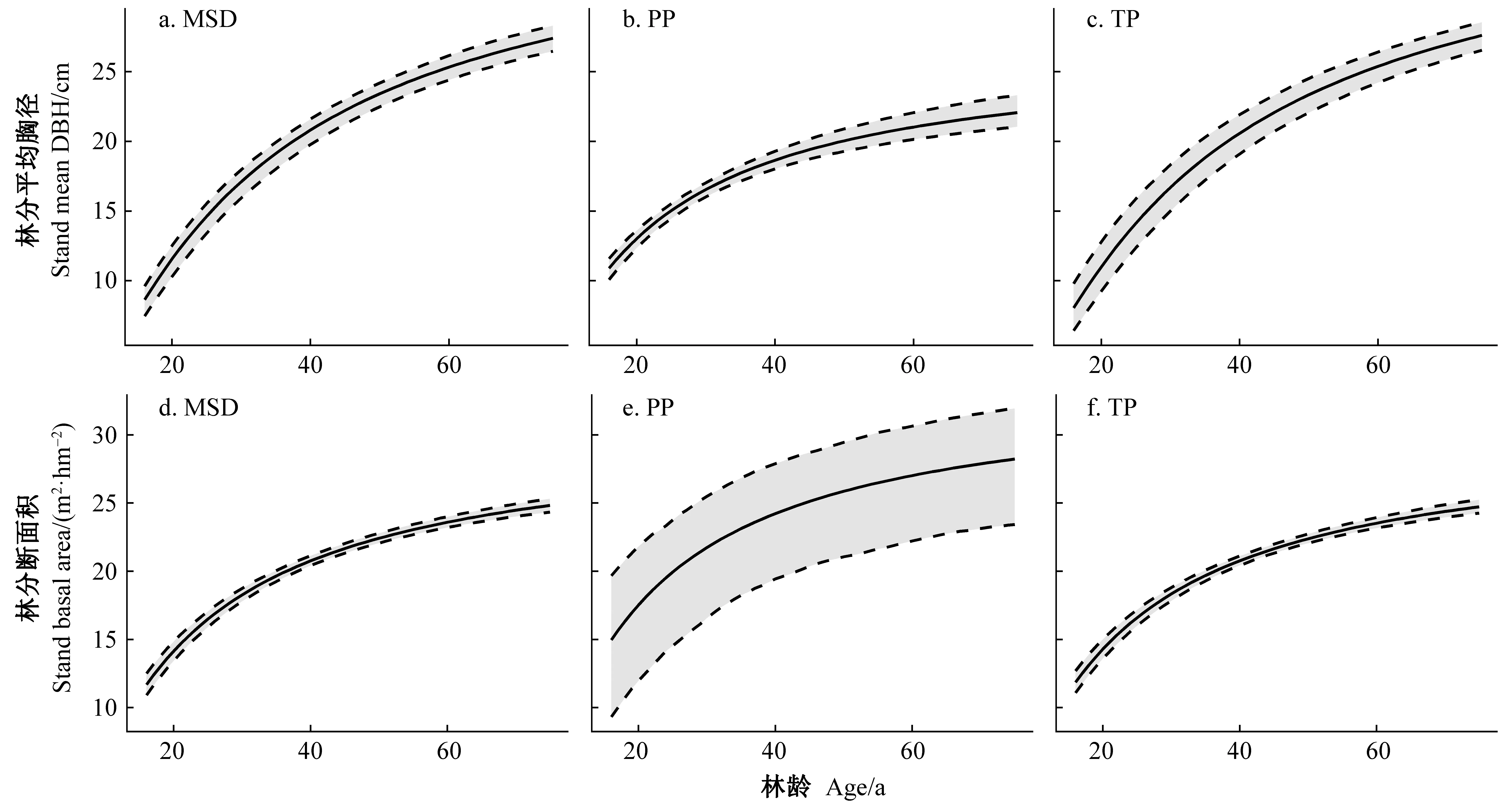
圖9 基于不同數據類型的林分平均胸徑和斷面積預測的更新變化過程(SCI=11, SDI=600)

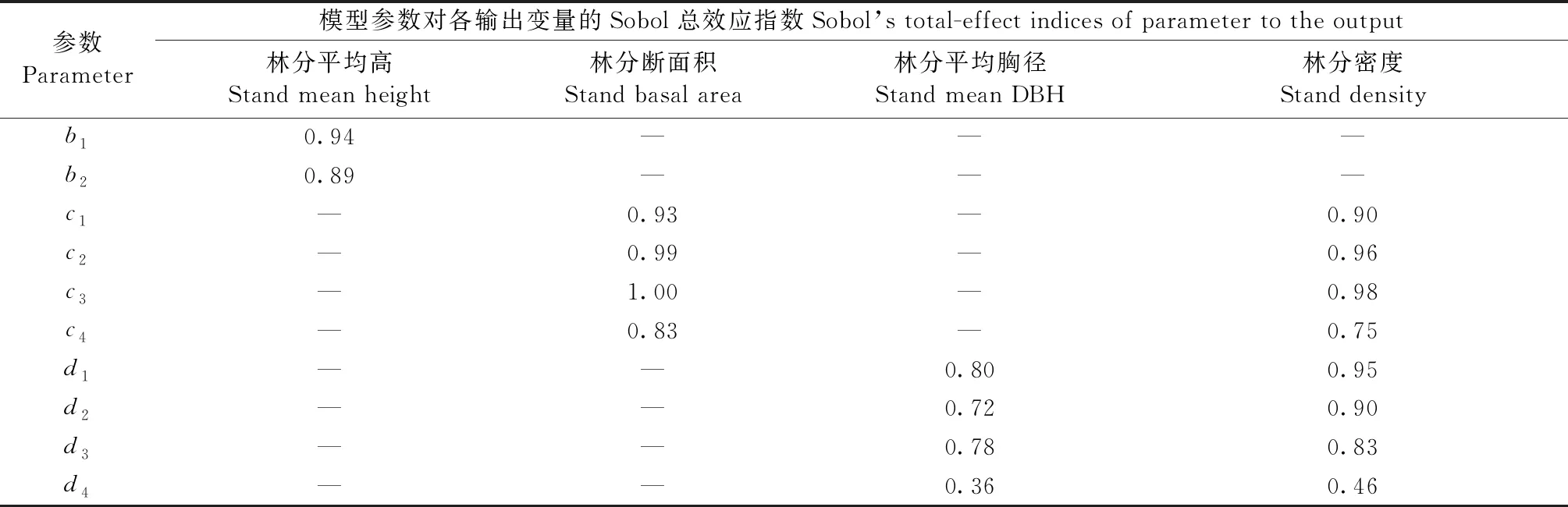
表5 基于方差的不確定性量化分解

模型預測的不確定性與建模數據本身規模直接相關。以林分斷面積為例(圖10)，當林齡為20、40、60年時，若抽選10塊樣地建模，1 000次重復后模型預測值波動標準差為1.77、1.40、1.90，而當樣地數量增加至200塊時，標準差則下降至0.44、0.27、0.30，這也直接解釋了圖9e中的較高不確定性實際是由固定樣地數據量較小造成的。隨著數據量增加，不確定性的降低速度逐步減緩，從10個樣本增加至20個樣本時，標準差減小14%； 從190個樣本增加至200個樣本時，標準差減小2%。

圖10 隨數據規模增加林分斷面積模型預測不確定性的變化過程(SCI=11, SDI=600)

3 討論

3.1 數據類型與抽樣方法對林分模擬的影響

本研究涉及的幾種數據類型各有其局限性，多源數據可避免某一數據類型缺陷過于嚴重傳遞至模型預測中。出于科研目的繼而提供精準信息的固定樣地長期觀測數據有著極高的經濟、人力和時間采集成本，通常可獲取數據量較少，很難涵蓋林分條件的變異幅度。臨時樣地成本低、數據量大，但與室內控制試驗不同，野外調查臨時樣地數據無法滿足抽樣均衡性，即不能保證各年齡階段樣地的立地質量分布和變異是否相似，容易在某個齡階出現有偏預測。解析木數據對林分整體狀況的代表性很難保證。以樹高生長為例，立地質量對林分生長動態具有直接影響，這意味著多源數據中的變異有特定比例可以被立地差異所解釋。在林分平均高、平均胸徑、斷面積模型中，基于林齡和林分平均高得到的地位級指數被用作解釋性變量，以描述不同立地條件下的林分生長收獲差異。為減小立地評價的系統性偏差，樹高導向曲線對抽樣均衡性有著極高要求，即各年齡階段樣地的立地質量分布和變異應是相似的，且單個樣地的立地質量在較長時期內保持一致。這些要求在多數情況下往往無法被完全滿足。在樹高導向曲線擬合中，解析木與樣地調查數據在樹木生長趨勢描述上有著明顯區別。理論上，解析木測量值比大多數樹高調查方法都更加準確，且能夠提供完整時間序列上的樹高動態信息，因此在樹高導向曲線中，本研究增加部分中等木和亞優勢木的樹干解析信息，以輔助解決幼齡林階段數據不足的問題，同時避免各年齡階段樣地立地質量分布差異導致的系統性偏差。本研究涉及林分為相對同齡而非嚴格同齡林，林木間存在一定程度年齡差異，作為樣本的中等木或亞優勢木可能在生命周期中相當長的時間內處于被壓迫狀態，而在樹高達到一定高度后從競爭壓力中恢復過來(Hannetal.， 2002)。另外，解析木選取常常基于樹木的干形和活力特征，這些都使得其樹高生長趨勢無法代表林分平均水平，且在成過熟林階段產生一定程度的高估(圖7g、7c)。當多源數據中不同數據集跨越較長時間尺度時，立地評價穩定性也會受多種因素影響，包括樹木子代個體基因型的改變(Monserudetal.， 1990)、氣候條件的改變(Bontempsetal.， 2009)、特定林分經營措施(Fox， 2000； Skovsgaardetal.， 2008)等。

盡管角規臨時樣地和矩形固定樣地均按照森林經理調查時分層抽樣與隨機抽樣相結合的準則設置，但在實際操作中，矩形固定樣地常常會被主觀建立在小班內坡度相對平緩的區域。相比之下，由于操作的便捷性，角規臨時樣地可以實現在平緩的下坡位和陡峭的山脊或陡坡均衡抽樣，而山脊或陡坡的林分常常因土壤瘠薄等因素生產力較低(Schrothetal.， 2003)。角規調查的缺陷是林下灌木、幼樹和地形等形成的復雜結構會造成繞測時視線遮擋(Van Laaretal.， 2007)。這些因素均會使得基于矩形固定樣地的斷面積生長量預測高于角規臨時樣地推算的結果(圖9e、8f)。

3.2 不確定性的量化

復雜非線性模型回歸分析通常被認為是優化問題。相比僅僅給出參數的最優估計值，貝葉斯方法通過MCMC抽樣技術獲得參數聯合后驗分布，使得模型中的信息可以更好體現在模型中。但即使是最優參數組合相同或相似，不同數據所給出的參數概率分布也可能存在很大區別，數據的異質性、觀測誤差、樣本數量等會反映到參數聯合后驗分布中，并最終影響模型預測的不確定性。對比圖5中2005和2012年數據組，或圖7、9中臨時樣地和固定樣地，最高概率曲線模擬的林分生長趨勢非常相似，但數據中的信息(如不同齡階時預測的可信區間)卻并不相同。基于1990年數據的預測在林分成過熟林階段有著很高不確定性，這是因為該階段的觀測較少且離散較高，而2005和2012年數據加入補充了成過熟林階段的林分信息(圖5)。大部分模型結果在林齡15～20年時均有著較高不確定性，這是因幼齡林階段數據缺失造成的，尤其在林分斷面積預測中最為明顯(圖9d、9e、9f)。整體而言，在不增加林分異質性信息的前提下，增大數據量是降低不確定性最直接的方法。相比林分平均高和平均胸徑，林分斷面積預測呈現出最高不確定性，且在數據量較低時差異尤為明顯(圖9e)。這說明對于林分斷面積而言，降低不確定性所需的數據量和抽樣調查的系統性都更高。影響林分動態的其他因素，如人為干擾、林型特征等，需要被更多地考慮到斷面積模型構建中，無論是2.1節的多期數據更新，還是2.2節的多種數據類型比較，綜合考慮全部信息的模型無論是參數還是預測均具有最高精度(最低不確定性)。

不確定性的解析式分解遵從Tylor展開式原理(Dietze， 2017)，貝葉斯方法以概率分布方式來描述參數和模型預測，由于本研究涉及的參數后驗概率分布不可解析，不確定性評估以Monte Carlo抽樣方法進行計算。需要強調的是，本研究涉及的數據和模型都較為簡單，因而只考慮了參數不確定性對預測的影響，并沒有涉及數據、模型結構、模型鏈接等部分的不確定性及其傳遞關系。在復雜模型的組合應用中，不確定性的傳遞與解構則是理解模型預測結果的關鍵性信息(Lebaueretal.， 2013)。

3.3 先驗的設計

不同于過程機制模型，經驗模型參數本身沒有實際生理學意義，很難給出準確合理的先驗設定。本研究沒有探討何種先驗是“好的先驗”，實際上討論的先驗都是基于以往數據信息，即基于往期數據得到的后驗作為模型更新時的先驗。以1990年數據進行首次擬合時，采用無信息先驗，即等同于極大似然：

p(θ1990|D1990)∝p(D1990|θ1990)。

2005年數據的模型校正，以1990年模型后驗作為先驗，即：

p(θ2005|D2005)∝p(D2005|θ2005)×p(θ2005)∝

p(D2005|θ2005)×p(θ1990|D1990)∝

p(D2005|θ2005)×p(D1990|θ1990)。

2012年數據的模型校正，以2005年一次校正模型后驗作為先驗，即：

p(θ2012|D2012)∝p(D2012|θ2012)×p(θ2012)∝

p(D2012|θ2012)×p(θ2005|D2005)∝

p(D2012|θ2012)×p(D2005|θ2005)×p(D1990|θ1990)。

當模型完成基于2012年數據的二次校正后，參數后驗同時包含1990、2005和2012年的數據信息。在這一模型循環更新框架下，如果有明確證據表明1990年數據不該作為2005年數據的先驗，那么就意味著這2期數據中有1期是錯誤的且應直接將其舍棄，但通常情況下，隨著數據積累，模型可靠性會逐步升高，新數據涵蓋了新的或更復雜的林分狀態信息。2005年數據校正和2012年數據校正模型變化幅度更小，則說明新增加數據提供的額外信息很少，不需要再投入過高成本對這些變化微小的變量繼續收集數據。本研究采用重尾正態分布降低異常值對模型擬合的影響，各期數據似然結構相互獨立，以避免精確數據被粗糙數據所稀釋。貝葉斯方法被廣泛應用于工程與信息科學的重要原因之一在于其高效的模型學習框架，這種高效性體現在當獲取到新一期數據對模型參數進行更新時，并不需要對新獲取數據的規模有任何特定要求(甚至1個觀測點即可)，模型更新也不需要重新提取整理往期數據，因為往期數據信息已包含在先驗中。

3.4 數據-模型關系

森林生態系統研究是一個漸進的過程，模型在該過程中至關重要。將已知信息作為先驗并與未來可能獲得的數據相結合，從而得到后驗和預測分布(Westetal.， 1997)，隨著數據積累逐漸更新對林分動態的理解，這一過程即數據-模型融合過程，其目的是使模型不斷吸收新的信息(Clark， 2007)。

模型的準確性和適用范圍取決于建模數據本身。理想情況下，模型構建和數據收集是不斷迭代的過程，模型設計決定數據需求，進而決定外業調查內容和方式； 然而森林生長周期漫長，獲取全部必要信息亦需漫長觀測周期，同時，選用不同數據也會對模型擬合造成明顯差異(Raulieretal.， 2003)，數據的類型、尺度、質量和規模等因素對模型構建與基于模型衍生的推論都有著重要影響。森林資源連續調查中，每一次調查分析結果都是下一次調查分析的最合理先驗(張雄清等， 2014)。森林生長收獲模型開發常常需要收集多個數據集信息，不同來源的數據在抽樣設計、觀測誤差和觀測數量等方面都會有所區別，而這些信息很難反映在模型的一組最優參數上。隨著信息數據加入，模型改變也并不局限于最優參數組合的調整。綜合考慮各數據組的誤差分布、異方差等問題，需要模型開發者針對不同數據集采用獨立的似然結構[式(9)]，不是簡單地將數據進行混合。而在數據不斷更新、模型學習并升級過程中，參數聯合后驗分布不斷改變(圖2和3)，進而導致預測的不確定性也在不斷發生變化(圖4和5)。在這種貝葉斯數據-模型框架中，數據與模型之間以概率分布形式融合為信息交互的循環體系。

本研究分析是基于貝葉斯框架下全林模型以聯立方程組方式進行參數估計的結果[將式(1)和式(3)代入式(5)和式(6)后進行聯立]，由此導致模型誤差的傳遞，即地位級指數模型和林分密度指數模型存在誤差，之后又將誤差引入林分斷面積和平均胸徑模型中。貝葉斯框架下聯立方程組比單獨擬合有著更為復雜的似然結構[式(12)、(13)]，相應地，模型開發者可以根據自身對數據和模型的理解來調整誤差分布和異方差假設，在擬合生長收獲模型參數的同時獲得描述誤差分布的參數估計值[式(10)、(11)]。聯立方程組模型中常見處理變量誤差和異方差的方式之一是進行對數轉換(洪玲霞等， 2012)，但對變量進行對數轉化本身并沒有生態學或生理學解釋，同時，基于模型輸出結果對變量進行逆向變換后預測結果也常常是有偏的(Dietze， 2017)。Zellner(1962)的似乎不相關聯立估計在考慮不同方程誤差項相關性的同時，也兼顧了異方差性問題，但較難與本研究的貝葉斯框架兼容。貝葉斯框架下進行似乎不相關回歸和聯立方程組回歸通常會圍繞基于協方差矩陣對聯立后參數條件概率與聯合后驗的推導計算(Andoetal.， 2010)，本研究完全依賴于集成Metropolis-Hastings算法的MCMC技術來實現對聯合后驗分布的抽樣和估計，從而最終實現將式(1)和式(3)代入式(5)和式(6)后所獲得聯立方程組的參數估計過程。考慮誤差傳遞的另一個重要方法是度量誤差效應模型(唐守正等， 1996； 1998)，該模型在貝葉斯框架下亦可實現(Clark， 2007； Clarketal.， 2007)，不僅地位級指數和立地指數評估的誤差在胸徑和斷面積模型中傳遞，而且森林調查中的胸徑、樹高、斷面積觀測誤差也可以被考慮。本研究所涉及的參數不確定性及其對預測不確定性的影響，僅僅只是不確定性或誤差分析的一部分內容，同時受限于數據規模和質量，在測試數據代表性和描述模型開發中不確定性傳遞上仍有諸多不足。

本研究采用貝葉斯數據-模型框架，出發點是為了兼顧不同數據集所具有的不同抽樣和觀測誤差，進而對不確定性進行量化。貝葉斯框架將模型校正和預測中的所有要素以概率分布方式進行處理(Clark， 2007； Dietze， 2017)，能夠方便實現以上目標。但需要強調的是，貝葉斯并不是實現這些目標的唯一方法，多源數據的觀測誤差處理可通過若干似然函數相乘或權重法設置目標函數來實現(Marleretal.， 2010)，抽樣方法的系統性誤差也可通過多層級的混合效應模型來評估(Bijleveldetal.， 1998； Wareetal.， 1996)，不確定性的量化則可依賴于自舉法來實現(Efron, 1979)。

4 結論

本研究以全林模型更新為例，描述貝葉斯框架下建模數據累積與生長模型不確定性循環學習的信息融合過程。結果表明，隨著森林調查數據不斷積累，模型參數和預測不確定性逐漸下降。建模數據信息中存在的缺陷可被量化并以不確定性方式直接反映在模型參數和預測中，進而為下一步模型改進與數據采集指明方向。多源數據的使用弱化了單一數據源中非均衡抽樣和異常觀測誤差對模型的影響，可有效提高林分動態預測質量。這種數據-模型循環更新和兼容多源數據的貝葉斯框架，同樣也適用于森林建模研究的其他諸多方向，如森林生產力、森林立地質量以及進界、自疏伐等森林動態與不確定性的研究和應用。