基于四元數的機械海流計姿態解算

劉慶鵬，于 雨，惠 力，魯成杰

(1.齊魯工業大學(山東省科學院)，濟南 250353；2.齊魯工業大學(山東省科學院)，山東省科學院海洋儀器儀表研究所，青島 266100)

0 引言

機械式海流儀經歷了幾代發展[1]，在其姿態角數據測量中，傳感器測量的數據經算法處理后，變為實時的角度顯示。而角度融合算法在工程上有幾種不同的方法[2]，采用歐拉角微分方程式需要進行三角函數的運算，且方程會出現“奇點”，方程式退化；用方向余弦法計算姿態矩陣，沒有方程退化問題，但需要求解6個微分方程，計算量較大，影響嵌入式系統的響應時間。文章采用四元數微分方程式，計算量不大且沒有“奇點”問題，并在實驗基礎上對算法可行性進行了驗證。

1 姿態解算原理

1.1 常用的坐標系

為了求解機械海流計的姿態角信息，引入北東地坐標系作為地理坐標系[3]。具體來說，OXg指向北方，OYg指向東方，OZg垂直指向地面。由機械海流計的縱軸OYb、橫軸OXb和豎軸OZb所構成的右手系作為載體坐標系，將兩個坐標系的原點定在機械海流計的質心，解算出地理坐標系和載體坐標系之間的角度關系即可求得機械海流計的姿態信息。

1.2 四元數解算原理

四元數是一種超復數，其形式可以表示為a+bi+cj+dk，有1個實部和3個虛部，其中a，b，c，d都是實數[4]。四元數可以用來描述機械海流計相對于地理坐標系的方向矢量，其中實部表示轉角大小，虛部表示轉動方向。通過四元數可以求出一個物體相對參考坐標系旋轉之后的坐標信息，參考坐標系和旋轉后的坐標系的轉換關系用變換矩陣式(1)來解算。

(1)

其中，q0代表實部；q1、q2、q3代表虛部。

物體旋轉后相對參考坐標系的角度變化信息也可以通過繞X軸旋轉一個角度(橫滾角)θ，繞Y軸旋轉一個角度(俯仰角)γ和繞Z軸旋轉一個角度(偏航角)φ來表示。3次旋轉過程可由姿態角變換矩陣來表示，姿態變換矩陣如式(2)所示。

(2)

式(1)和式(2)均為物體從參考坐標系變換到載體坐標系，所以兩個變換矩陣相等。由此可建立起四元數組成的矩陣與方向余弦矩陣之間的關系，可以通過反三角函數求取3個歐拉角[5]，公式如下：

橫滾角：

(3)

俯仰角：

γ=-arctan(2(q1q3+q0q2))

(4)

偏航角：

(5)

只需要知道四元數的4個參數，就能解算出物體的姿態角。

海流計處于動態之中，故四元數是一個隨時間變化的函數。建立四元數微分方程如下：

(6)

式(6)中，d0、d1、d2、d3表示更新后的四元數；ωx、ωy、ωz是由陀螺儀測量得到的機械海流計繞載體坐標系三軸旋轉的角速率。實際計算中將四元數微分方程離散化，使用一階龍格-庫塔法得到更新后的四元數，則有：

(7)

式中，T表示姿態解算當前時刻，T+ΔT表示姿態解算下一時刻。從式(7)可看出，理論上只需要得到3個繞軸角速率便可以通過四元數法求出物體的歐拉角。而MEMS陀螺儀根據角動量守恒原理可以精確地測量角速率，但由于溫度變化、摩擦力、不穩定力矩等因素，陀螺儀會產生漂移誤差，通過積分會使誤差變大。該誤差可以通過加速度計進行矯正，當加速度計在沒有加速度的狀態下，加速度計的輸出是一個幅度為1 G地球表面的法向量。通過該法向量，可以計算出羅盤相對于地球表面的俯仰角和橫滾角，利用這兩個角可以在機械海流計近乎勻速的情況下修正陀螺儀產生的累計誤差。文章采用六軸的處理組件MPU6050(包括三軸加速度計和三軸陀螺儀)，通過四元數算法對HMC5883L得到的流向進行傾角誤差補償。

2 測量電路

測量電路采用InvenSence公司的MPU-6050六軸傳感器芯片和Honeywell公司的HMC5883L磁阻傳感器芯片[6]，將二者組合相連用以測量加速度數據A、陀螺儀數據G和地磁場數據M。姿態解算電路如圖1所示。

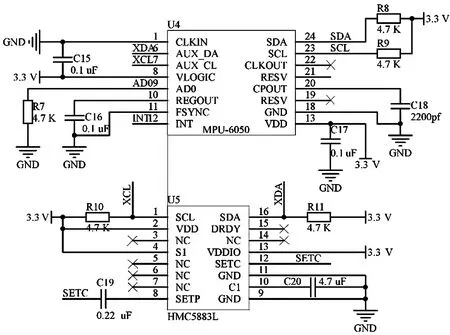
圖1 姿態解算電路

陀螺儀和加速度計都集成在MPU6050傳感器芯片上，其測量范圍達到±16 g。芯片正常工作時，MPU6050采用I2C接口與控制芯片連接，SDA和SCL信號線需要接入4.7 kΩ的上拉電阻以增加驅動能力。讀取芯片數據首先要進行初始化，需要配置電源管理，陀螺儀采樣頻率、低通濾波頻率、陀螺儀自檢及測量范圍和加速度計自檢、測量范圍及高通濾波頻率。初始化后，陀螺儀采集科里奧利力在3個軸上形成的電壓值，加速度計采集1 G的地球表面法向量在各軸的分量形成的電壓值，經過16位A/D轉換器轉換為數字信號，利用預設的比例關系將其換算成實際的角速度值和角度值。

HMC5883L三軸磁場強度敏感芯片內置ASIC放大器，工作頻率達160 Hz，羅盤航行精度精確至1°～2°，同樣使用I2C總線輸出。芯片的SCL和SDA分別接到MPU6050的AUX_CL和AUX_DA，同時接入4.7 kΩ的電阻來增加驅動能力。磁阻傳感器主要用于測量地磁場矢量，定位海流計的方向(定位流向)。

3 具體姿態解算過程

3.1 三軸磁羅盤組件HMC5883L測流向

帶有磁阻傳感器的線路板封裝在機械海流計旋槳殼體內，安裝時將X軸指向旋槳方向，Y軸指向旋槳右側，Z軸垂直于其他兩軸指向海底。海流計尾翼隨海流方向的變化而變化，旋槳相應調整方向并指向海流方向。磁阻傳感器感應地磁場變化，采集各軸方向上的磁場強度。

磁場水平分量HN與磁場垂直分量Hz的矢量和表征地球磁場強度[7]。磁場水平分量HN總是指向地球磁場北極，利用該特性，若想測出流向，只需要測出旋槳方向(載體坐標系X軸和磁場水平分量之間的夾角)即可。磁阻傳感器感應到X軸的磁場強度為Hx，Y軸的磁場強度為Hy，其矢量和為地磁場水平分量HN。地磁場水平分量HN與X軸之間的夾角即為方位角α，已知方位角即可知流向[8](圖2)。

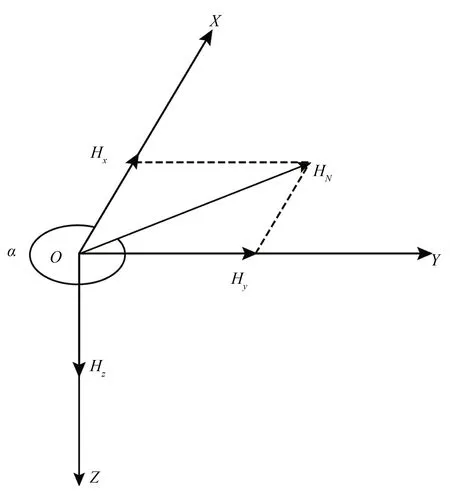
圖2 磁阻傳感器處于水平狀態的坐標系

根據圖2，由三角函數可求得方位角為[9]：

(8)

3.2 MPU6050修正流向

在實際應用中，磁阻傳感器坐標系和海流計載體坐標系重合，假設載體坐標系和地理坐標系重合，則海流計測得的磁場強度HB為：

(9)

式(9)中，HN為地磁場水平分量，其方向與載體坐標系X軸重合，在Y軸上的分量為0；Hz為地磁場垂直分量，其方向與Z軸重合。

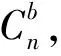
(10)

(11)

式(11)中，q0、q1、q2、q3是MPU6050所測數據更新后的四元數(標量)；Hbx、Hby和Hbz分別為當地地磁強度在3個軸上的磁場分量。通過式(3)和式(4)可得X軸與水平面之間的俯仰角γ，Z軸與過X軸的鉛垂平面之間的橫滾角θ，結合磁阻傳感器測出的地磁場在三軸的方向分量，重新計算得到水平方向分量Hx2和Hy2計算其方位角。由坐標關系得水平方向磁分量：

(12)

將Hx2，Hy2帶入式(8)計算即可得到方位角。

由于磁力線在地球表面分布的大小和方向存在差異，所以地球南北極和地磁南北極之間的磁偏角也是因地而異。要得到真方位角，只需在計算出的方位角基礎上加上或減去當地的磁偏角。查出所在海域的磁偏角β，則真方位角ρ為：

ρ=α+β

(13)

3.3 軟件實現

文章利用C語言編寫軟件程序，且采用調試更為方便的模塊化設計，以便快速獲取海流流向信息。軟件功能主要包括初始化系統參數、磁場數據和姿態角數據的采集、方位角的解算、磁偏角矯正以及真北顯示輸出等，軟件處理流程如圖3所示。

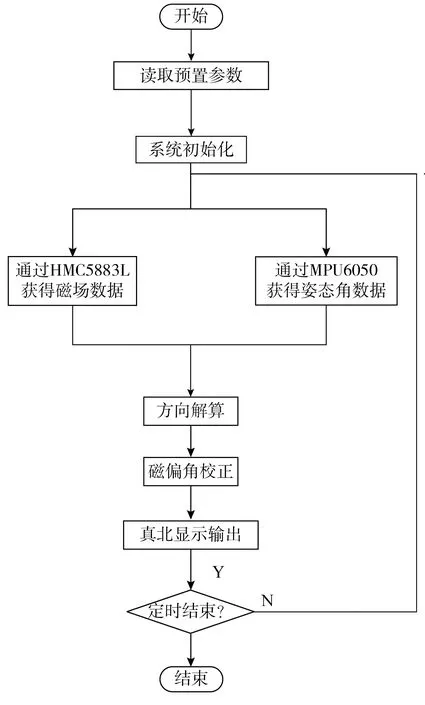
圖3 軟件處理流程

4 調試與實驗

為驗證文章所采用的姿態解算算法的有效性，對以姿態算法為原理搭建的機械海流計進行測試。實驗的主控制器選用STM32F103RCT6，姿態檢測單元選用MPU6050和磁阻傳感器HMC5883L，配合CAN總線收發模塊及最小系統模塊完成對姿態數據的采集、處理、通訊以及顯示。

實驗步驟如下：

1)在保持海流計水平狀態下，使其做原地旋轉運動，取定點測量，并進行數據的采集和解算；

2)對海流計進行人為擾動，在海流計不能保持水平狀態的情況下，使其做原地旋轉運動，取定點測量，并進行數據的采集和解算。

經多次測量，發現在定點處測量的數據在兩種狀態下得到的流向基本一致。說明使用該算法能夠很好地處理海流計在不平衡狀態下的傾角補償問題，能夠測出準確的流向數據。

5 結束語

文章利用磁阻傳感器HMC5883L測出海流計的流向，分析了方向余弦與四元數之間一一對應的關系，并用MPU6050結合四元數算法解算出機械海流計的姿態角，用姿態角對海流計流向進行修正。文章結合實驗驗證了四元數法在姿態解算中的應用，通過設計海流計的姿態解算模塊，給出了四元數具體的應用過程。為海流計在任意姿態下進行流向測量提供了保障。