基于模糊自適應PID的卷繞系統張力控制

陳明霞，鄭海濤，尹浚成，趙金迪

(桂林理工大學 機械與控制工程學院，廣西 桂林 541004)

在生產制造、機械加工中，大多數是使用多臺電動機同步協調運作組成卷繞控制系統。張力控制是卷繞系統中的關鍵環節，是為了卷繞材料在卷取以及開卷過程中保持張力恒定或者在某一特定范圍內，其廣泛應用于紡織、造紙、印刷、橡膠等行業中。在生產制造過程中，卷繞系統對張力的大小有著嚴格的控制要求。張力太大將會使得生產制造的卷繞材料被過大的張力拉斷；張力不足也會引起材料在卷繞的過程中產生褶皺或者卷繞材料脫落的現象；而張力不穩定又將使產品的品質受到影響，因此，在卷繞過程中，往往需要將卷繞材料的張力變化保持在所允許的范圍內[1-2]。

因為常規PID具有原理簡單，容易實現且魯棒性強和適用面廣的特點，并且還具有能改善系統的動態特性以及穩態特性的優點，因此在傳統的張力控制中一般都是采用常規的PID控制。但是常規PID一般對模型的精確性要求較高，對于具有非線性、時變性并且容易受隨機干擾的卷繞張力控制系統而言，并不能取得良好的張力控制的效果[3-4]。查閱國內外張力控制研究成果，大部分還是在設備上進行改進從而提高設備控制精度，但是這種方法成本較高并且維護難度較大。為了解決上述問題，本文提出了一種模糊自適應PID控制卷繞系統張力的方法，使得卷繞系統具有自動整定控制參數的能力，可以在生產中適應被控對象的變化，并且在實驗平臺上，實際的卷繞系統張力控制中取得了良好的控制效果。

1 卷繞系統張力控制模型

一個完整的卷繞張力控制系統一般由收放卷機構、控制和張力檢測裝置以及輔助裝置等組成[5-6]。實際應用中，卷繞張力系統也可由其中的部分組成，卷繞系統結構簡圖如圖1所示。放卷輥、收卷輥在相應的伺服電動機的控制下進行開卷、卷取卷繞材料，張力傳感器感知卷繞材料的張力，系統根據張力設定值與實際值之間的差值相應地控制放卷輥或者收卷輥的電動機速度，進而調整系統的張力，因而卷繞系統的張力是基于速度差原理產生的，控制張力就是控制放卷輥與收卷輥的速度差。

圖1 卷繞系統結構簡圖

卷繞材料在卷取的過程中被拉伸，如果形變在其彈性形變范圍內，那么卷繞材料兩端的張力則滿足胡克定律。研究卷繞系統的張力時，忽略其他因素的情況下，可以將該系統的張力分析簡化[7-9]，整個過程可以簡化成如圖2所示的簡圖。

L—形變后卷繞材料長度(m);V放—放卷輥速度(m/s);V收—收卷輥速度(m/s);D放—放卷輥直徑(m);D收—收卷輥直徑(m)。

根據胡克定律，張力分析為：

(1)

(2)

(3)

式中：σ為卷繞材料受到的應力，Pa；ε為卷繞材料產生的彈性形變；E為卷繞材料的彈性模量，N/m2；T為張力，N；A為卷繞材料的橫截面積，m2；L0為卷繞材料產生的絕對形變量，m；L為當前狀態下因張力產生形變后的卷繞材料長度，m。

當V放≠V收時，t+dt時間內，張力變化如下：

(4)

由于應力σ引起的形變ε?1，則：

(5)

(6)

V=πDn

(7)

式中：n為收放卷輥的轉速，rad/s；D為收放卷輥的直徑，m。

整理以上各式可得卷繞材料張力為：

(D收n收-D放n放)dt

(8)

綜合以上各式說明卷繞過程中卷繞材料受到的張力是由放卷輥和收卷輥之間的速度差產生的，要使得張力控制在一定值，則要控制好收放卷輥的速度，同時由式(8)可以看出，這是一個時變、非線性的系統，用傳統的PID控制系統很難實現良好的控制。

2 模糊自適應PID控制器設計

2.1 模糊自適應PID控制器原理

卷繞系統將張力設定值作為輸入，將收放卷輥的伺服電動機轉速作為輸出，利用模糊自適應PID控制器以及張力傳感器進行對系統的反饋調節。將卷繞材料張力的偏差e和偏差變化率ec作為模糊自適應PID控制器的輸入，制定相應的模糊規則控制表，以參數Kp,Ki,Kd修正量作為輸出，根據模糊推理方法對Kp,Ki,Kd實現在線調試，使其與偏差e和偏差的變化率ec相匹配，從而滿足對PID參數的自適應要求[10]。控制結構如圖3所示。

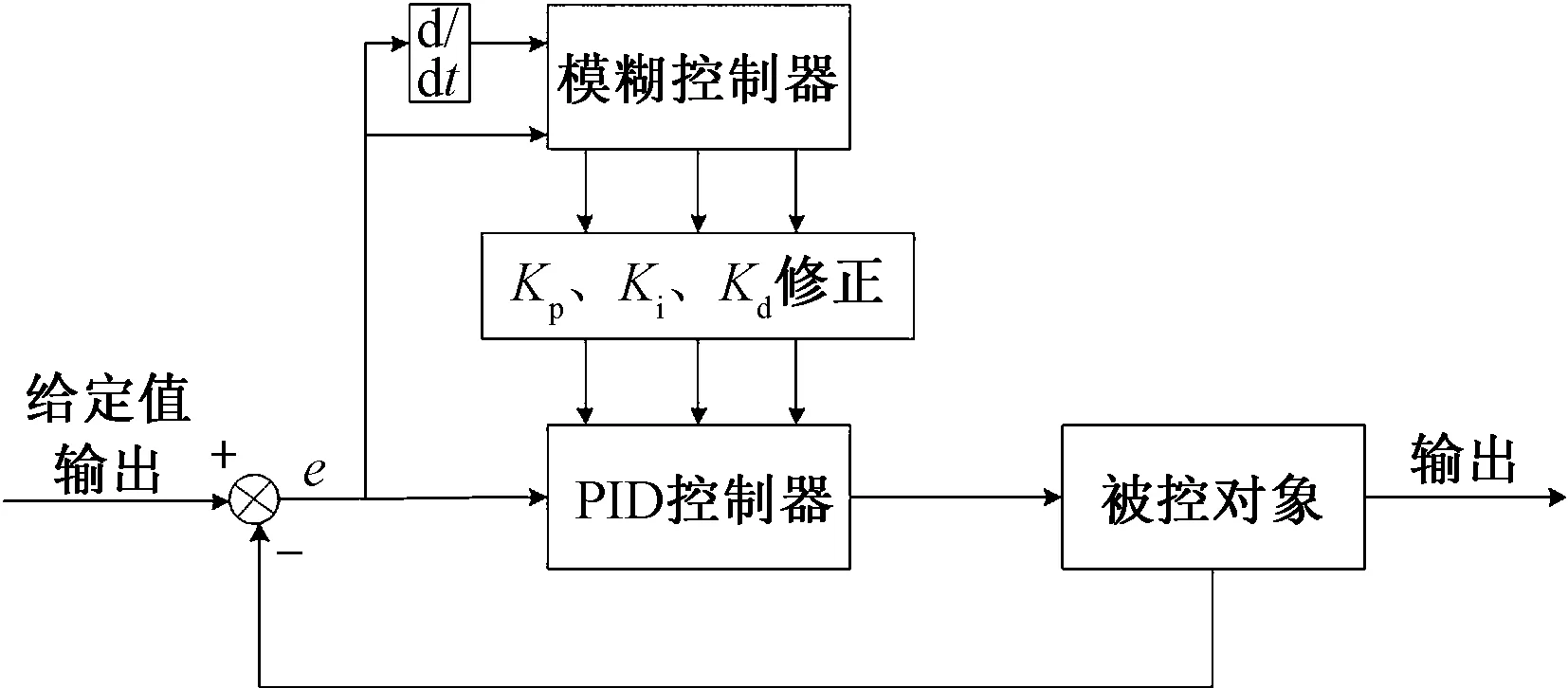
圖3 模糊自適應PID控制器結構圖

2.2 模糊變量論域隸屬度函數

將e和ec設為輸入變量,ΔKp、ΔKi和ΔKd設為輸出變量，模糊語言集均為：{NB，NM，NS，ZO，PS，PM，PB}，即{負大，負中，負小，零，正小，正中，正大}。e和ec的離散論域設為{-6，-5，-4，-3，-2，-1，0，1，2，3，4，5，6}，ΔKp、ΔKi和ΔKd量化論域設為{-6，-5，-4，-3，-2，-1，0，1，2，3，4，5，6}。量化因子取Ke=0.6，Kec=0.6，比例因子Kup=0.22，Kui=1和Kud=1。

使用陡峭的隸屬函數可以使得控制獲得較高的分辨率，以及提高控制的靈敏度；使用平緩的隸屬函數會降低控制的靈敏度。在實際的應用中，離系統平衡點較遠偏差較大時，可以使用低分辨率隸屬函數；靠近平衡點偏差很小時，可以使用高分辨率隸屬函數。本次實驗中采用三角形隸屬度函數，其中e、ec；ΔKp、ΔKi、ΔKd的隸屬度函數如圖4所示。

圖4 e、ec、ΔKp、ΔKi、ΔKd的隸屬度函數

2.3 模糊控制規則的建立

在模糊控制系統中，其主要核心為模糊控制規則表[10-11]，其作用相當于是傳統控制系統中的校正器或補償器[12-14]。對于需要滿足不同的e和ec以及對控制參數的要求不同，因此根據此規則制定相應的模糊控制規則表。使得控制對象能有良好的動態和靜態性能。模糊規則控制表如表1所示。

表1 Kp/ki/Kd的模糊控制表

2.4 清晰化

在模糊控制中，對于模糊量的清晰化是非常重要的環節，因為經過模糊邏輯推理后，輸出的是模糊集合，要將模糊集合等效成一個清晰值，然后才能將其應用于系統的控制當中。加權平均法、最大隸屬度法以及中位數法等都是清晰化常用的方法。其中加權平均法較為適用于精度要求較高的系統，故本文實驗采用加權平均法。

采用加權平均法計算控制器的輸出ΔKp、ΔKi、ΔKd，表達式如下：

(9)

式中:μuj(ΔKu)為P、I、D 3個參數的第j級隸屬度，ΔKuj為P、I、D 3個參數的第j級元素加權系數。

PID參數的整定表達式為：

Ku=Ku0+ΔKu

(10)

式中：Ku0為傳統PID控制3個參數的初始值；Ku為PID控制系統參數變化值和初始值的總和；ΔKu為PID控制系統參數調整時的變化值。

3 仿真實驗及其結果分析

圖5 卷繞控制系統仿真模型

在仿真實驗中，用階躍信號作為實驗的輸入信號，在系統運行平穩后，在20 s時將輸出信號幅值改為2，觀察傳統PID控制和模糊自適應PID控制2種算法下系統的適應情況。實驗結果如圖6所示。由MatLab/Simulink的仿真結果觀察可得，模糊自適應PID控制比傳統PID控制具有更快的響應，上升時間4.0 s優于傳統PID的4.1 s，迅速達到穩態值，最大超調量控制在1%，可認為沒有產生超調，優于傳統PID的8%，調節時間5.0 s優于傳統PID的9.6 s。2種算法的控制性能如表2所示。

表2 不同算法控制性能仿真比較

圖6 仿真結果

為了進一步驗證模糊自適應PID算法的實際應用效果，在西門子卷繞系統實驗平臺上進行傳統PID控制和模糊自適應PID控制的實驗對比分析，實驗平臺如圖7所示。

圖7 卷繞系統實驗平臺

建立系統的項目函數，將在MatLab/Simulink中實現的模糊自適應PID控制算法在全局腳本編輯器中用C語言進行編程實現。一般情況下，考慮實際系統的控制時效性，在實際的計算機控制中，模糊自適應PID控制算法一般通過查詢模糊控制表的方法實現。

①通過全局腳本查詢模糊控制表。

//變量e對應(-6,6)進行等級化處理

e=ac-sp; //實際誤差值e

if (e<0) //先判斷e的正負，方便下一步進行四舍五入

E=(int)((ke*e)-0.5); //將e進行四舍五入然后轉換成對應的等級量

else

E=(int)((ke*e)+0.5);

if (E>m)

E=m;

if (E<-m)

E=-m;

i=E+m+1; //得到對應的E在模糊控制表的位置

//變量ec對應(-6,6)進行等級化處理

e0=GetTagFloat(“ec0”); //獲取上一狀態誤差值

ec=e-e0; //當前誤差減去上1個誤差

if (ec<0) //先判斷ec的正負，方便下一步進行四舍五入

EC=(int)((ke*e)-0.5); //將ec進行四舍五入然后轉換成對應的等級量

else

EC=(int)((ke*e)+0.5);

if (EC>m)

EC=m;

if (EC<-m)

EC=-m;

j=EC+m+1; //得到對應的EC在模糊控制表的位置

WinCC的全局腳本編輯器能夠實現2種不同函數的生成，一種是項目函數，另一種是動作函數。2種函數實現的功能是完全不同的。項目函數和高級語言中使用的函數功能相似，是用來實現設定的計算、數據處理等功能，但是項目函數是不能夠被直接執行的，必須使用主函數的調用才能夠進行相應的功能。而動作函數則不一樣，其只需滿足設定條件就可以自動執行相應的動作。因此，在實際工程應用上，在WinCC中一般通過項目函數實現較為復雜的數據計算、處理等算法功能，然后在動作函數中進行調用該項目函數實現算法控制，只要滿足動作函數的觸發條件，項目函數可以根據動作函數不斷自動執行。

②通過動作函數中調用項目函數。

#include "apdefap.h"

int gscAction(void)

{

// WINCC:TAGNAME_SECTION_START

// syntax: #define TagNameInAction “DMTagName”

// next TagID: 1

// WINCC:TAGNAME_SECTION_END

void fuzzypincontrol ();

float sp=GetTagFloat(“張力設定值”); //獲取設定值sp

floatac=GetTagFloat(“張力實際值”); //獲取實際值ac

floate=sp-ac;

floatwc=e/sp; //穩態誤差控制在3%以內

intstpid;

stpid=GetTagBit(“st”);

if(((wc>0.03)||(wc<-0.03))&(stpid==1)) //誤差超出3%則進行模糊PID調整參數

{

fuzzypidcontrol ();

}

// WINCC:PICNAME_SECTION_START

// syntax: #define PicNameInAction “PictureName”

// next PicID: 1

// WINCC:PICNAME_SECTION_END

return 0;

}

卷繞系統在運行時，2種算法參數的設置為：傳統PID控制器中的參數為kp=0.10，Ti=15，Td=0，模糊自適應PID控制算法中，量化因子e=0.6，ec=0.6，比例因子kep=0.001 5，kei=0.005 5，ked=0。

當卷繞控制系統在設定張力值為60 N時，傳統PID控制的效果和模糊自適應PID控制下的效果如圖8所示。

與傳統PID控制相比，在最大超調量的控制上，模糊自適應PID算法控制更有效地降低了系統的最大超調量，在張力值為60 N時，系統的最大超調量為3.01%，已經進入控制系統的5%穩態誤差帶，系統的穩定性更強；在系統的調節時間方面，模糊自適應PID算法控制的系統調節時間明顯更短，在張力值為60 N時，系統響應上升后直接進入了穩定狀態；同樣，在峰值時間和響應的上升時間上，模糊自適應PID算法控制總體上均優于傳統PID控制，能夠更快地到達相應的狀態。一般情況下，穩態誤差保持在5%以內即可視為系統已經穩定，在穩態誤差的控制方面，模糊自適應PID算法控制優于傳統PID控制，更能降低穩態誤差，使系統更加接近系統設定值，更好地滿足實際工程應用的需要，獲取良好的控制效果。2種算法控制下的實驗結果性能比較如表3所示。

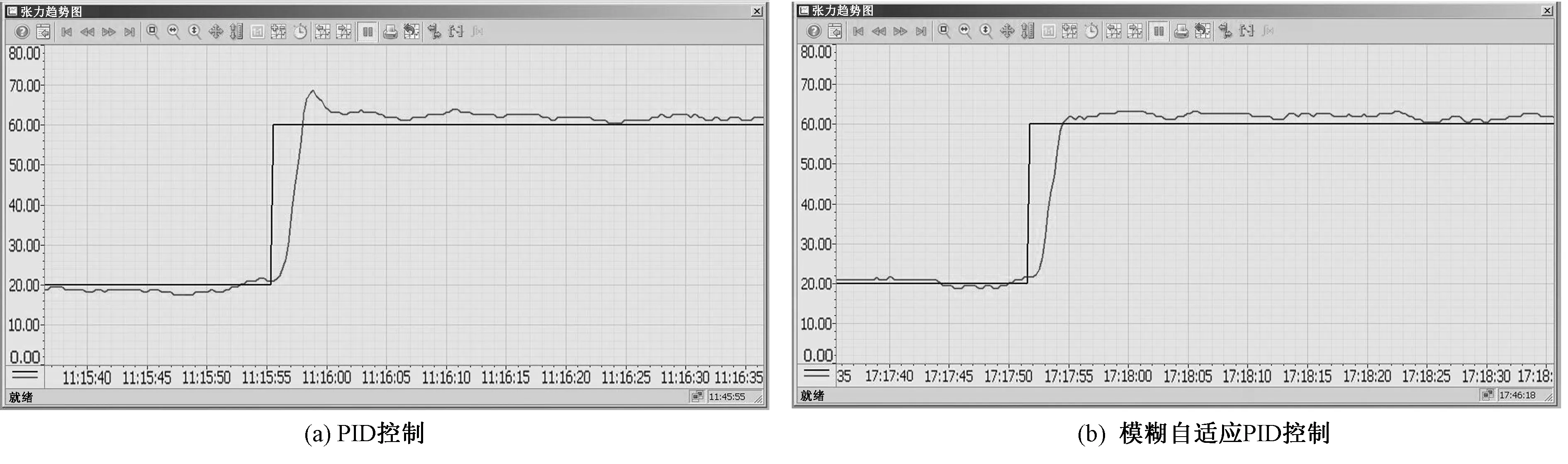
圖8 張力趨勢實驗結果對比

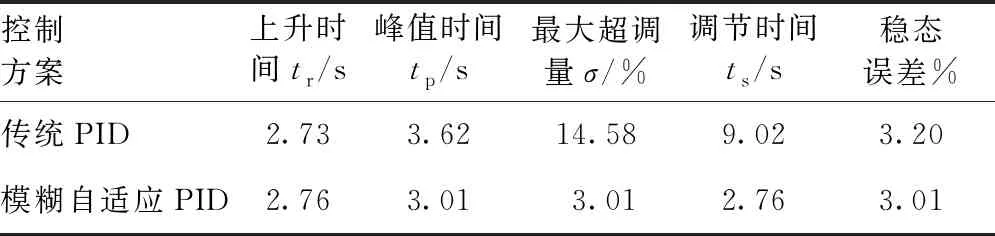
表3 2種算法控制性能實驗比較

4 結束語

在實際工程應用中，系統的時效性和穩定性尤為重要，模糊自適應PID算法控制與傳統PID控制相比而言，更能適應具有明顯的時變性、不確定性等特點的卷繞控制系統，表現出良好的適應性和較強的魯棒性，獲得更好的控制效果，滿足實際工程應用的需要。模糊自適應PID控制算法通過在上位機中WinCC全局腳本中進行算法運算，該模式下可以降低PLC的運載負荷，減少PLC的內存占用。同時，在全局腳本中編程與PLC中編程相比，編程的復雜程度降低，程序的可讀性更高，靈活性高。同時也驗證了模糊自適應PID控制算法在運用到實際卷繞控制系統中具有一定的可行性。