大型客機柔性后緣增升裝置氣動機構一體化優化設計

張雅璇 劉沛清 夏 慧 戴佳驊 李慶輝 欒博語

(北京航空航天大學，北京 100191)

0 引言

增升裝置設計技術的重大突破對進一步提高新一代民用客機的氣動性能起著關鍵性作用，這在世界范圍內也是一個很有挑戰性的研究課題[1]。為了達到降低油耗、減少噪聲和污染的目標，高效航空發動機技術、復合材料機身、高效增升裝置技術等多種先進技術和新能源技術都被應用到民用航空運輸當中。如今，增升裝置設計需要多學科設計優化，這已在飛機設計中進行了大量的研究，國外R.C.Potter與L.P.Yip[2-3]等人提出一種反映氣動性能、結構重量和成本的設計方法，國內唐家駒[4]等人借鑒了A350和波音787的后緣增升裝置及其機構特點，搭建了大型飛機增升裝置氣動機構一體化優化設計平臺。戴佳驊[5]等人以簡單鉸鏈為驅動機構，開展了起降構型的同步優化和機構設計工作。陳亞璨[6]等人針對驅動機構為連桿滑軌的翼型，進行了“后緣襟翼+擾流板同時下偏”的優化設計工作。

柔性機翼可以改變機翼展向和弦向的彎度，進而改變機翼表面的氣體流動，提高氣動效率，減少燃油消耗以及溫室氣體排放，可以調整展向載荷分布以減小翼根彎矩，還可以有效抑制激波，擴大抖振邊界，能獲得較剛性機翼更好的性能。正因為柔性變彎機翼這些優勢的存在，可變彎度機翼成為未來大型飛機的研究熱點。波音公司1980年的研究結果表明變彎度構型顯著提高了整個飛行剖面非設計點的氣動性能[7]。隨著材料的不斷發展，近年來，可連續變彎度的智能材料機翼成為了研究的熱點[8]，但是想要在工程上實現還有一定的困難。J.A.Hetrick[9]等人研究了任務自適應柔性機翼，飛行試驗的結果表明在大部分范圍內，升阻比可提高15%或者是更多。美國空軍實驗室的J.J.Joo[10-11]等人研究了“可變彎度機翼”，對比了機翼整體變彎和后緣部分機構變彎，結果表明在小迎角時整體變彎的機翼阻力更小，升阻比更大。T.Yokozeki[12-13]等人使用波浪結構來使襟翼變彎，該結構的驅動力較低，在小迎角時有較好的氣動性能。沈廣琛[14]等人研究了一套可用于現在和未來的民用客機機翼后緣變彎增升裝置系統，提高了升力系數和升阻比。陸維爽[15]等人針對GAW-1翼型，進行了前后緣變彎度的氣動性能的研究，明顯改善了翼型的爬升性能。田云、全建沖[16]等人以NASA TrapWing模型為基礎，提出了一種“柔性前緣下垂+單縫鉸鏈襟翼+擾流板下偏+柔性尾緣襟翼”的智能增升系統，并進行多學科優化，得到氣動、機構、結構綜合最優的起降構型。王瑞[17]等人以DLRF11機翼為研究對象，設計一套基于反平行四邊形機構的后緣襟翼柔性變彎機構，進行二維起降構型的氣動/機構一體化優化設計，優化結果提高了起降構型的氣動性能，巡航時的氣動性能也有所改善。

本文以某大型寬體客機內段襟翼為基礎，在襟翼內部安裝一套柔性變彎機構，之后在該柔性變彎機構的帶動下使襟翼實現柔性變彎，并且在后緣鉸鏈襟翼機構的帶動下使襟翼發生偏轉，來進行起飛和著陸構型的三維機構運動導引下的二維氣動/機構一體化的優化，優化目標以滿足氣動性能為主。

1 后緣襟翼柔性變彎機構介紹

以某大型客機內段機翼為研究對象，在襟翼后緣后50%部分的內部安裝一套柔性變彎機構，要求該機構簡單、重量輕。在該機構的帶動下，襟翼后50%部分可以實現柔性變彎，襟翼前50%部分為剛性的，圖1所示為巡航時的襟翼，CFlap為襟翼弦長，圖中展示了巡航構型的柔性變彎位置，也就是后50%CFlap。

圖1 襟翼巡航構型柔性變彎位置示意圖

柔性變彎機構的機構簡圖如圖2所示，圖中只展示了襟翼的后50%部分，該機構由兩級旋轉機構組成，三角形A1A2A3為第一級旋轉機構，三角形A3B1B2為第二級旋轉機構，這兩個三角形在A3處用鉸鏈進行連接，A2為固定鉸支，固定在襟翼的后梁上，用連桿將柔性變彎機構與襟翼蒙皮上的桁條進行連接。當OE1桿向前推動后，兩級旋轉機構就會向下偏轉，襟翼也就會在連桿的帶動下實現柔性變彎。變彎后的翼型與原始未變彎的翼型對比如圖3所示，在原始剛性襟翼的基礎上，柔性變彎后的襟翼可使襟翼后緣增加8°的偏角。

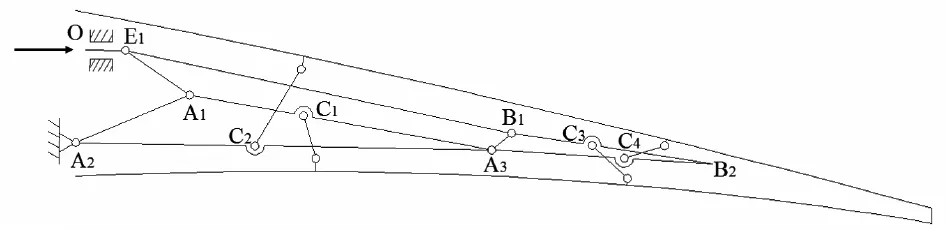
圖2 柔性變彎機構的機構簡圖

圖3 柔性變彎后的翼型與原始未變彎的翼型對比

新一代先進增升裝置以A350XWB和波音787的增升裝置為主，在其后緣增升裝置中采用主動控制技術，使擾流板聯合單縫襟翼同時下偏。單縫襟翼的機構采用簡單鉸鏈，簡單鉸鏈襟翼雖然沒有富勒襟翼實現的富勒運動大，但是鉸鏈襟翼可以使襟翼機構的復雜度降低，而且重量輕。為了減小襟翼打開時擾流板后緣和襟翼之間的間隙，需要在襟翼打開時使擾流板下偏，這樣可以提高氣動性能[18]。本文針對的某大型寬體客機內段機翼的前緣增升裝置采用前緣下垂，后緣為簡單鉸鏈襟翼聯合擾流板下偏。

內段襟翼所采用的機構如圖4所示，機構點上標i表示內側機構，機構點上標o表示外側機構，R表示轉動副，S表示球面副。內段襟翼為定軸轉動，軸線為Ei和Eo兩點所連的直線。

圖4 內段襟翼機構

2 二維柔性增升裝置氣動機構一體化優化設計

2.1 計算方法與數值驗證

因為沒有帶前緣下垂的二段翼的風洞實驗數據，所以選用二維三段翼30P30N來進行數值驗證。30P30N是公布于上世紀美國NASA的計算多段翼繞流的標準二維翼型，在多段翼型的CFD計算驗證中使用的非常廣泛。30P30N模型的參考弦長Cref=1 m，計算工況為馬赫數Ma=0.2，雷諾數Re=9×106，網格量為13萬，遠場邊界前緣和上、下部分為40倍參考弦長，后緣為80倍參考弦長，第一層網格高度為10-5倍弦長，網格如圖5所示。計算求解器采用ANSYS CFX，湍流模型為SST。

圖5 30P30N網格

計算結果對比美國Douglas飛機公司[19]和NASA Langley研究中心的風洞實驗結果[20]，圖6中所示的為襟翼、縫翼、主翼的升力系數以及總升力系數隨迎角的變化曲線的計算結果與實驗數據對比，從圖中可以看出，總體上看升力系數數值計算值與實驗值基本吻合，縫翼在高迎角時的數值計算值略大于實驗值，在23°時發生失速，比實驗值晚了2°失速。

圖6 30P30N升力系數的數值計算與實驗數據對比

圖7為8°迎角下，30P30N的壓力系數的數值計算結果與實驗值的對比，從總體上看數值計算值與實驗值吻合較好，縫翼上翼面的數值計算值略小于實驗值，襟翼上翼面的數值計算值略大于實驗值，襟翼尾緣部分略有偏差。

圖7 8°迎角下30P30N壓力系數的計算值與實驗值對比

總體來看，數值計算的結果與實驗值吻合較好，所以認為數值計算的結果是可行的。

2.2 氣動機構一體化優化設計

本文以某寬體客機的內段外側順氣流機構布置剖面為原始構型，干凈構型的弦長c=8 270.415 mm，采用“前緣下垂+擾流板下偏+后緣鉸鏈襟翼+襟翼后緣柔性變彎”的增升裝置設計方案，在內段襟翼機構的三維運動的帶動下，同時后緣襟翼柔性變彎機構帶動襟翼后緣進行柔性變彎，在襟翼和擾流板繞各自軸運動到不同位置后截取同一順氣流位置的剖面，對起飛構型和著陸構型分別進行二維增升裝置氣動機構一體化優化設計，優化在ISIGHT軟件中進行。均采用正置翼進行計算，并將計算結果轉換到斜置翼上。

起飛時的優化變量共有7個見表1，分別為：擾流板下偏角度、襟翼下偏角度、柔性變彎機構驅動桿OE1移動距離、襟翼轉軸點Ei的x坐標、襟翼轉軸點Ei的y坐標、襟翼轉軸點Eo的x坐標、襟翼轉軸點Eo的y坐標，柔性變彎機構驅動桿移動距離也就決定了襟翼柔性部分的下偏量，各優化變量的取值范圍如表1所示。大型民用飛機在起飛時，需要較大的升力系數以及升阻比以增加飛機爬升梯度、減小發動機推力，因此優化目標有2個，分別為8°迎角下升力系數最大、8°迎角下升阻比最大。優化算法選取非支配排序遺傳算法(Non-Dominated Sorting Genetic Algorithm-II，簡稱NSGA-II)。設置計算20代，每代24個子代，共計480個計算工況。

表1 起飛優化變量

著陸時的軸線就采用起飛時優化出來的軸線，著陸時的優化變量有3個，分別為：擾流板下偏角度、襟翼下偏角度、柔性變彎機構驅動桿移動距離，各優化變量的取值范圍如表2所示。優化目標與起飛不同，著陸時飛機的升力系數是唯一需要考慮的因素，而升阻比則不需要考慮，因此優化目標只有一個，為8°迎角下升力系數最大，為單目標優化，因此采用多島遺傳算法(Multi-island Genetic Algorithm)，共計500個計算工況。

表2 著陸優化變量

后緣襟翼柔性增升裝置氣動機構一體化優化流程如圖8所示。首先進行襟翼后緣柔性變彎的有限元計算，需要在MATLAB中生成在改變后緣柔性增升裝置中驅動桿推動的距離后得到的可以在ANSYS APDL中進行自動計算的APDL程序；然后在ANSYS APDL中通過運行MATLAB中生成的APDL程序，可以自動進行有限元計算，得到柔性變彎后的翼型；之后在MATLAB軟件中進行翼型參數化，使得在改變優化變量的值后可以自動得到新的起飛或著陸翼型；接著用POINTWISE軟件進行網格自動劃分；然后使用CFX軟件進行自動氣動計算；最后進行優化，得到氣動性能最優構型。

圖8 后緣襟翼柔性增升裝置氣動機構一體化優化流程圖

3 二維柔性增升裝置氣動機構一體化優化設計結果

3.1 起飛構型優化結果

起飛構型在ISIGHT中進行480輪優化，得到的優化結果如圖9所示，橫坐標為升力系數，縱坐標為升阻比，Pareto前沿在圖中也可看出，從Pareto前沿上選取A、B、C三個點進行分析。

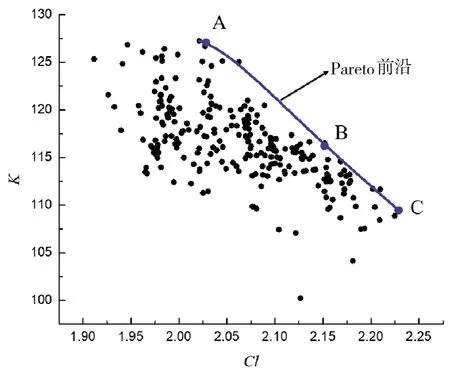
圖9 起飛構型優化結果

A、B、C三點的翼型與原始翼型的對比如圖10所示，從圖中可以看出，三組翼型襟翼尾緣的下偏量依次增大。這三組構型的優化變量的值以及原始構型的優化變量的值如表3所示，三組構型以及原始構型的縫道參數gap和overlap如表4所示。

圖10 三組構型翼型對比

表3 三組構型的優化變量以及原始構型的優化變量

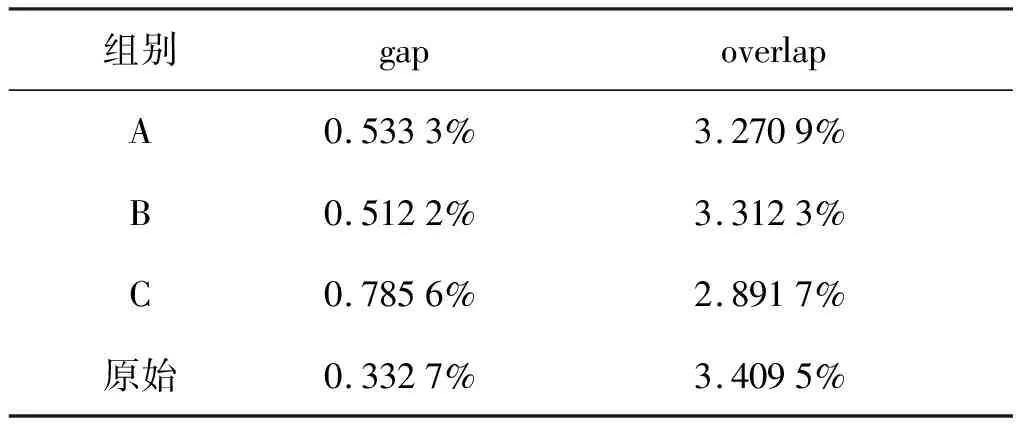
表4 三組構型以及原始構型的縫道參數

這三組構型的氣動性能與原始構型的對比如圖11所示。從圖(a)中可以看出，A、B、C三組構型與原始構型相比，升力系數都有所增加，A構型增加的最少，C構型增加的最多。A構型在13°時失速，B構型在12°時失速，C構型在12°時失速。從圖(b)中可以看出，A、B、C三組構型與原始構型相比，阻力系數也都有所增加，A構型增加的最少，C構型增加的最多。從圖(c)中可以看出，A、B、C三組構型與原始構型相比力矩系數都有所減小，A構型減少的最少，C構型減少的最多。從圖(d)中可以看出，當升力系數較小時，只有A構型的升阻比是大于原始構型的，升力系數較大時，三組優化構型的升阻比都大于原始構型。

(a)升力系數對比

綜合而言，A構型的升力系數有所增加，在升力系數較小和升力系數較大時A構型的升阻比都有所增加，因此選取A構型為最優構型。A構型的最大升力系數與原始構型相比的增加量為0.119。圖12所示為8°迎角下最優構型的壓力系數與原始構型的壓力系數的對比，從圖中可以看出，最優構型和原始構型下翼面的壓力系數相差不大，前緣以及襟翼的吸力峰增加。

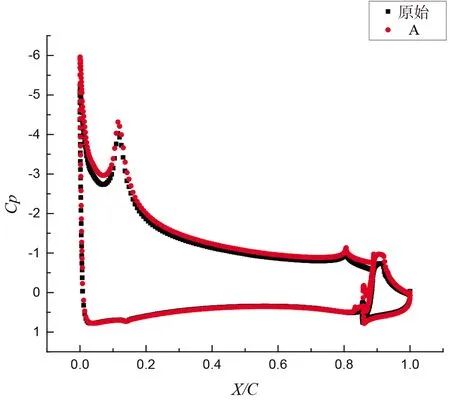
圖12 8°迎角下起飛最優構型的壓力系數與原始構型對比

圖13為起飛最優構型的壓力云圖及流線圖，從圖中可以看出，在8°迎角下，起飛最優構型未發生分離，在13°迎角下襟翼上表面即將發生分離，14°迎角下襟翼上表面有分離渦的出現，發生分離，15°迎角下襟翼上表面有更大面積的分離渦產生，發生大面積分離。

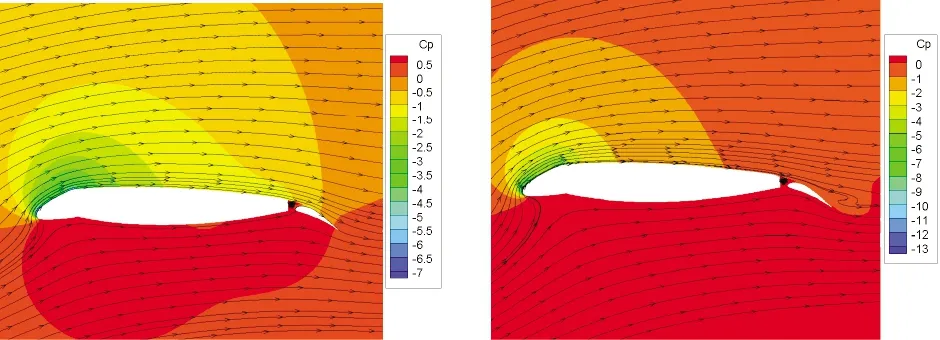
(a)8°迎角 (b)13°迎角

3.2 著陸構型優化結果

著陸構型在ISIGHT軟件中共進行500輪優化，得到的最優構型和原始構型的翼型對比如圖14所示，最優構型襟翼尾緣的下偏量與原始構型相比有所增大。著陸最優構型以及原始構型的優化變量的值如表5所示，縫道參數gap和overlap的值如表6所示。

圖14 著陸最優構型與原始構型的翼型對比

表5 著陸最優構型以及原始構型的優化變量值

表6 著陸最優構型以及原始構型的縫道參數的值

著陸最優構型與原始構型氣動性能的對比如圖15所示，從圖(a)中可以看出，著陸最優構型在11°時失速，比原始構型晚1°失速，最大升力系數為2.604。線性段最優構型和原始構型的升力系數相差不是很大，最優構型的升力系數略微大于原始構型，在失速段最優構型的升力系數明顯大于原始構型。從圖(b)中可以看出，除11°迎角以外，其余迎角下的最優構型的阻力系數均大于原始構型的阻力系數。從圖(c)中可以看出，線性段的力矩系數最優構型和原始構型相差不大，失速段最優構型的力矩系數小于原始構型。最優構型的最大升力系數比原始構型的最大升力系數提高0.162。

(a)升力系數

圖16為著陸最優構型與原始構型8°迎角下的壓力系數的對比圖，從圖中可以看出，最優構型后緣襟翼前緣的壓差較原始構型相比有所增大。

圖16 8°迎角下著陸最優構型的壓力系數與原始構型對比

圖17為著陸最優構型的壓力云圖及流線圖。從圖中可以看出在11°迎角時即將失速，此時襟翼后部還是存在分離區，12°迎角時緊貼襟翼的分離區消失，流動存在附著流，存在分離渦，此時已經失速。14°迎角時襟翼尾緣存在更大面積的分離渦。

(a)8°迎角 (b)11°迎角

4 結論

1)本文基于某大型寬體客機內段襟翼，在后緣鉸鏈襟翼機構的帶動下，并且襟翼后緣在柔性變彎機構的帶動下實現柔性變彎，進行了起飛和著陸構型的氣動/機構一體化優化設計。起飛優化出的最優構型與原始構型相比，最大升力系數的增加量為0.119，并且在相同的升力系數下，升阻比有所增大。

2)著陸優化出的最優構型與原始構型相比，最大升力系數的增加量為0.162，且最優構型推遲1°迎角失速。

3)優化所得的起飛和著陸構型均提高了原始構型的氣動性能。