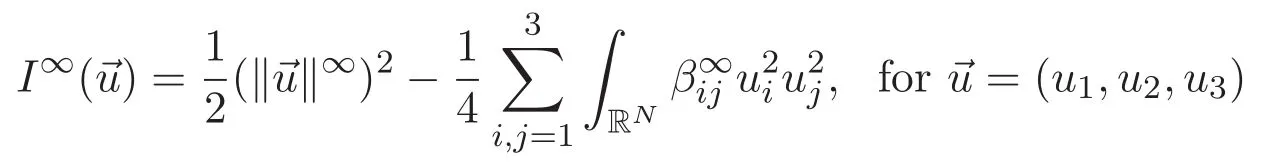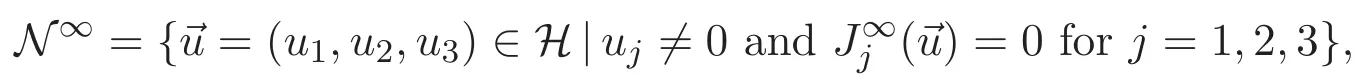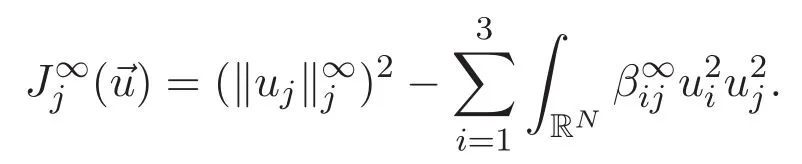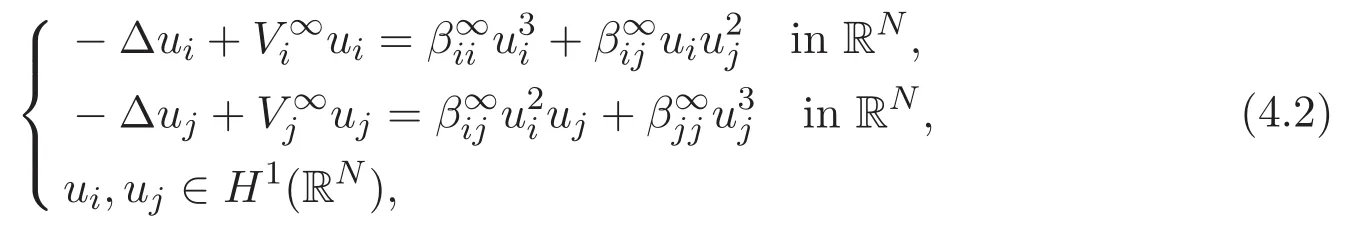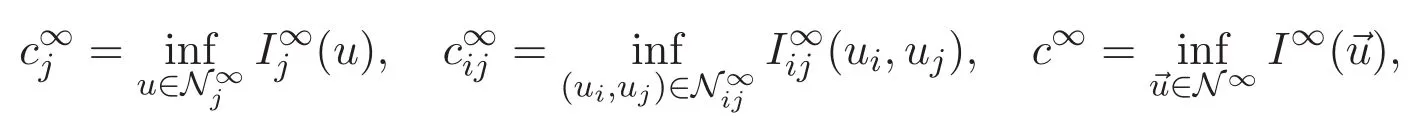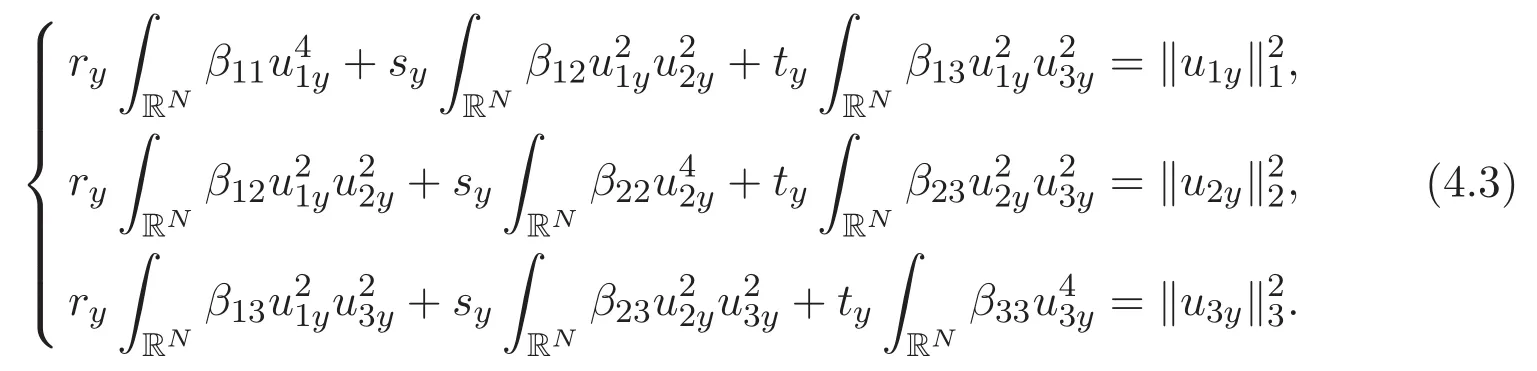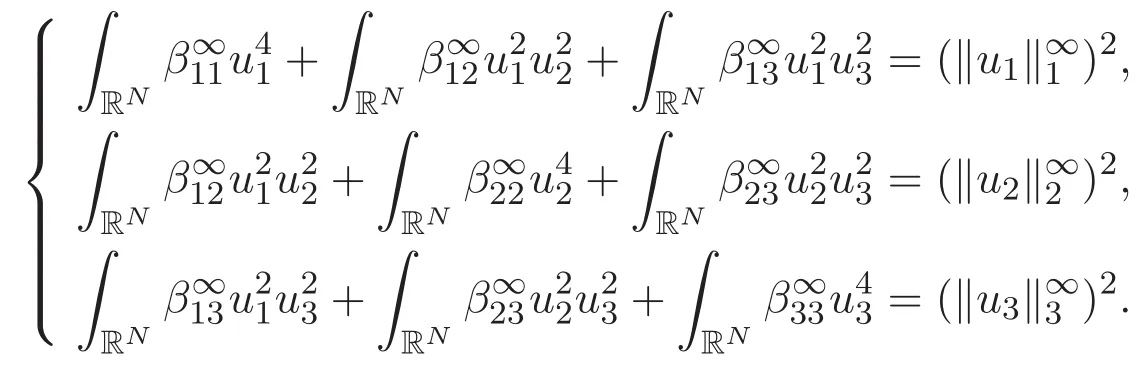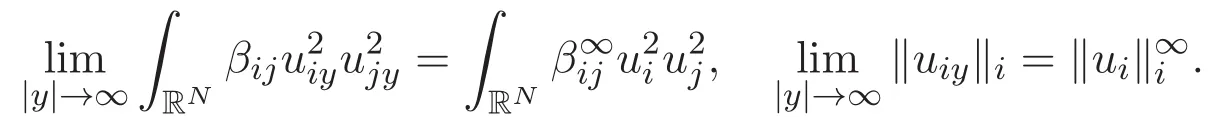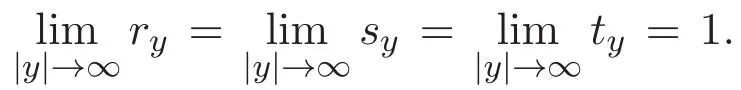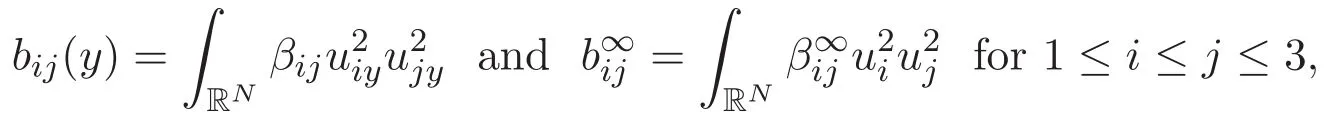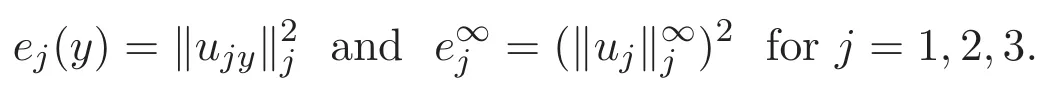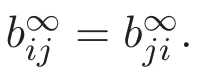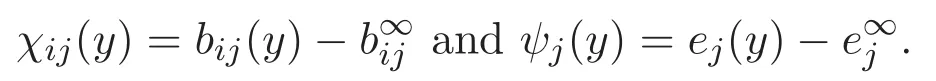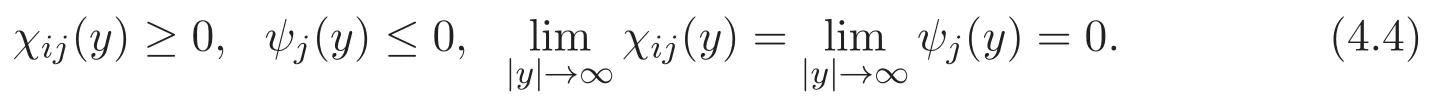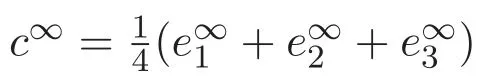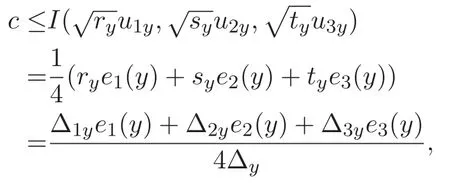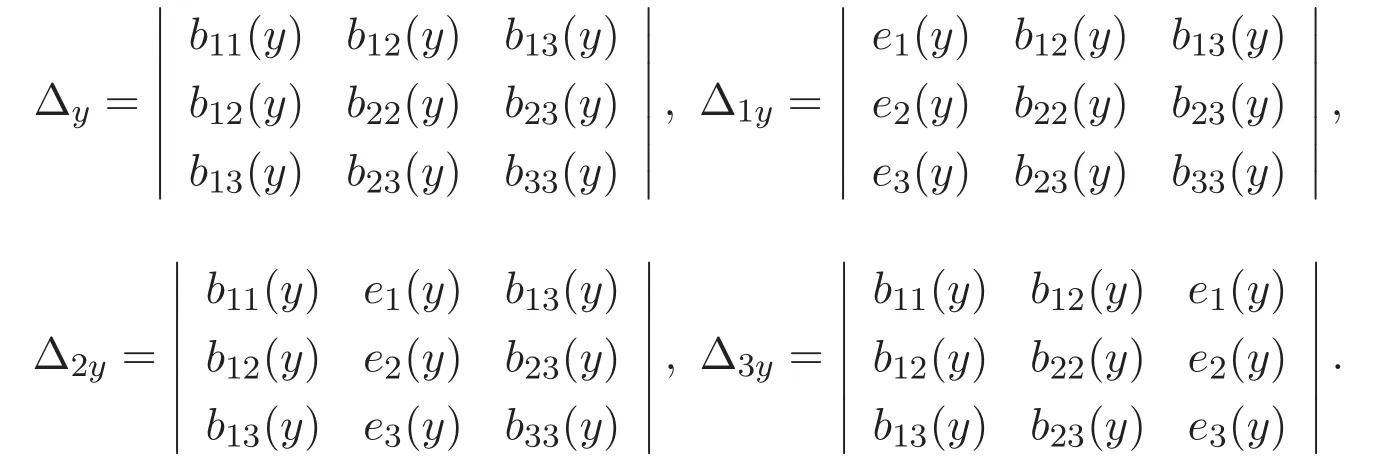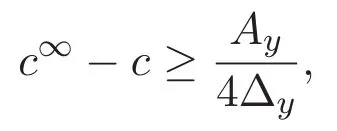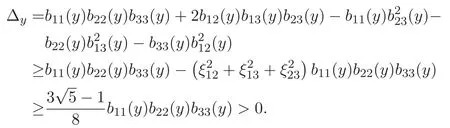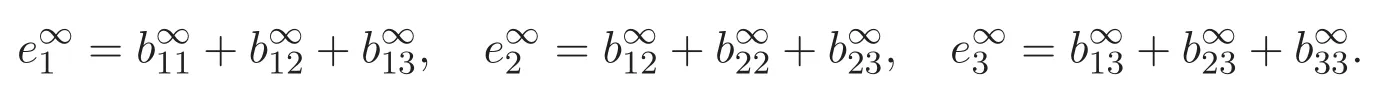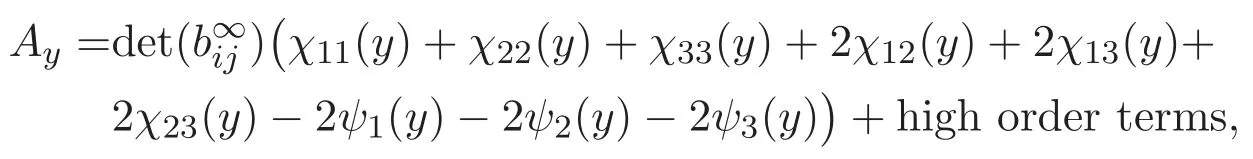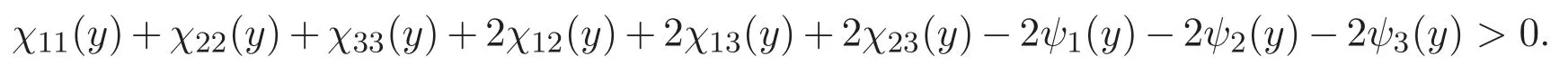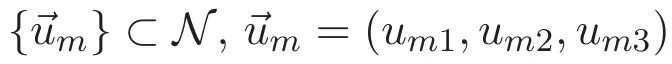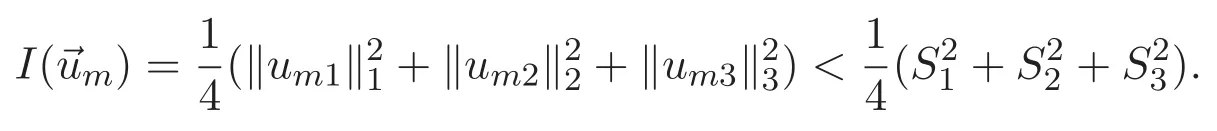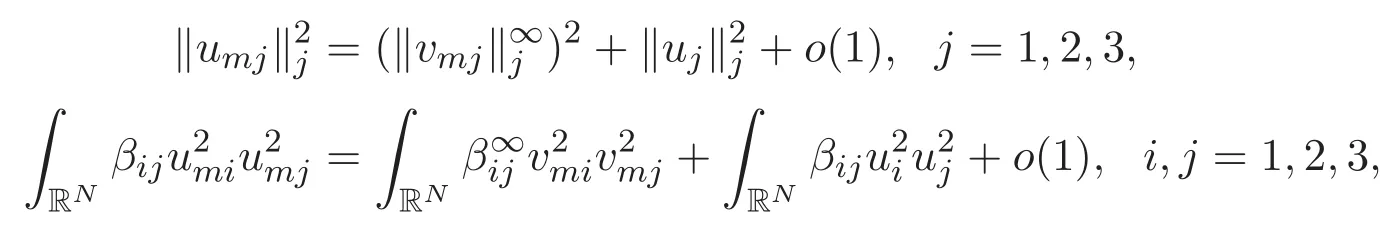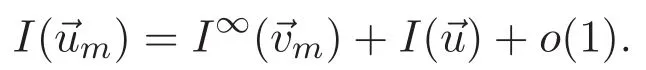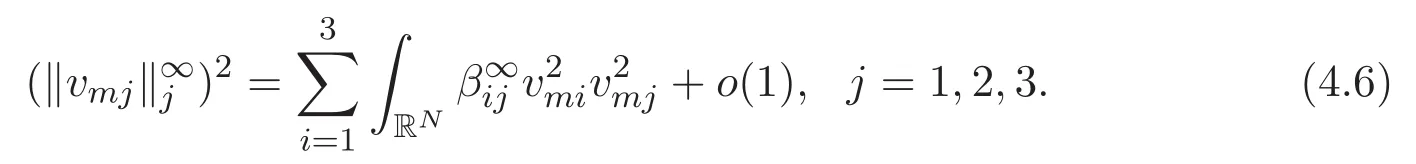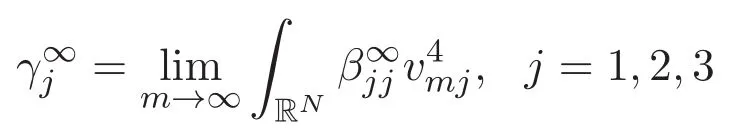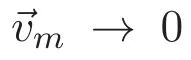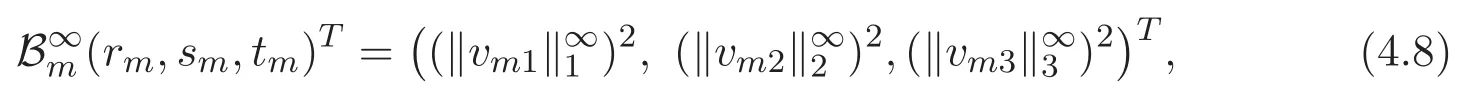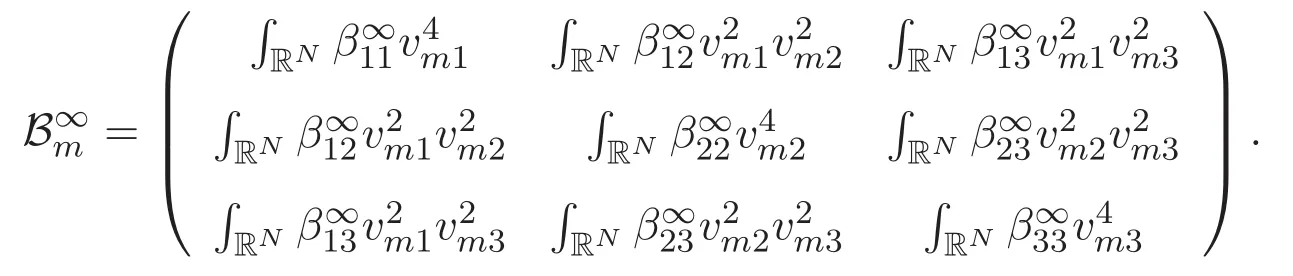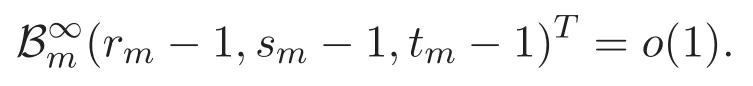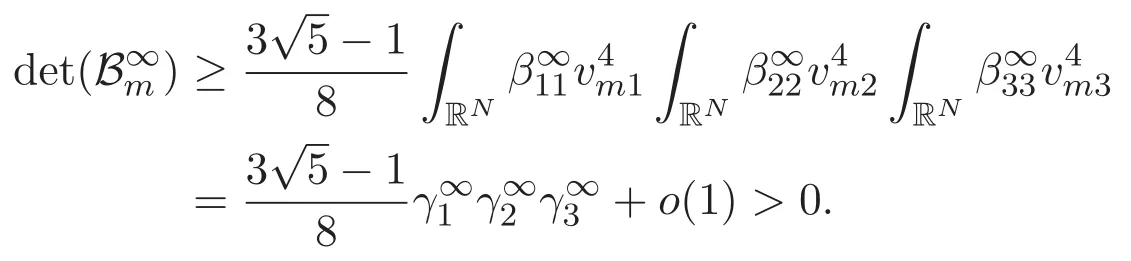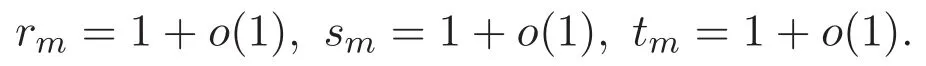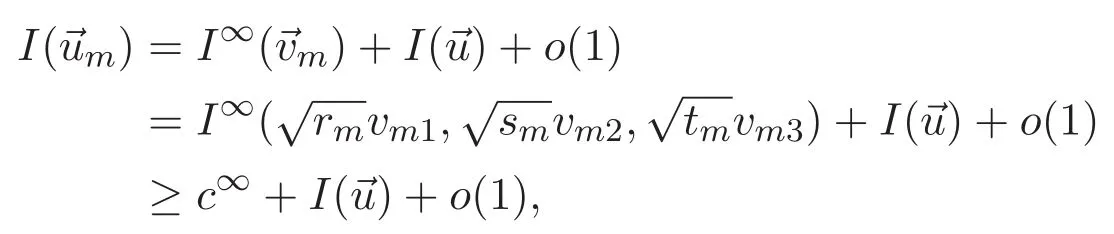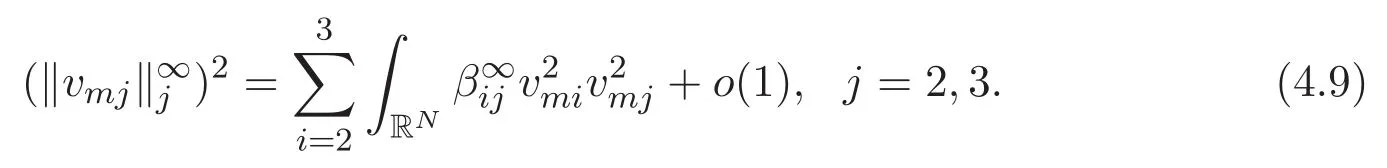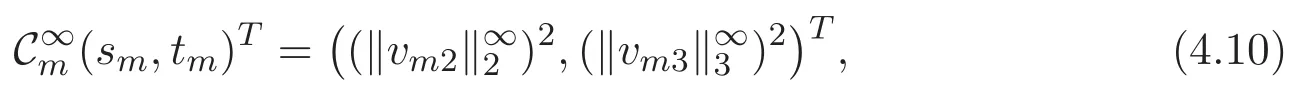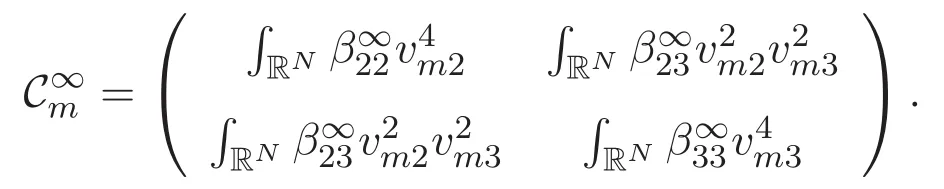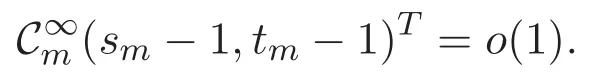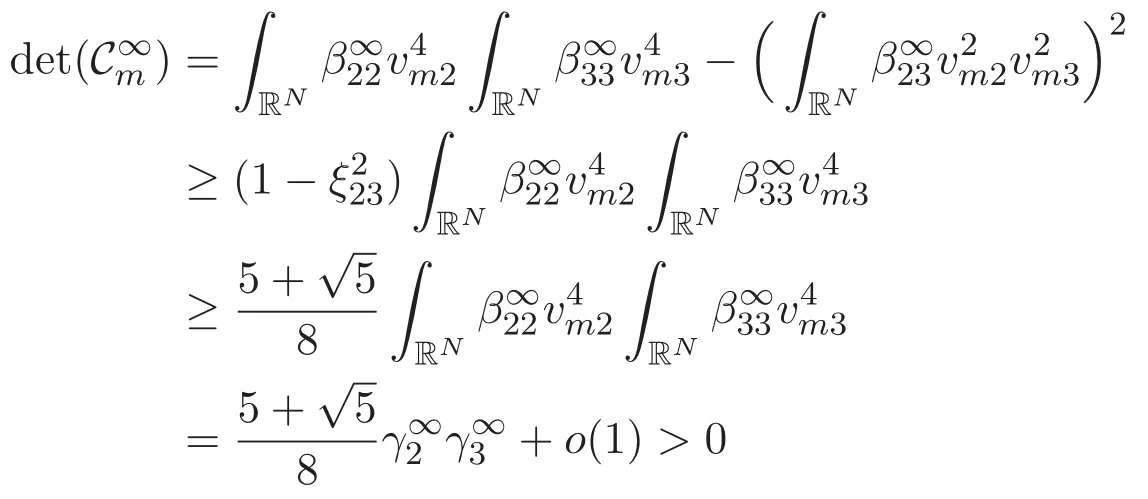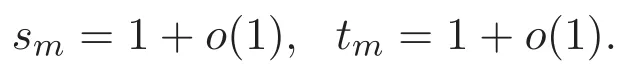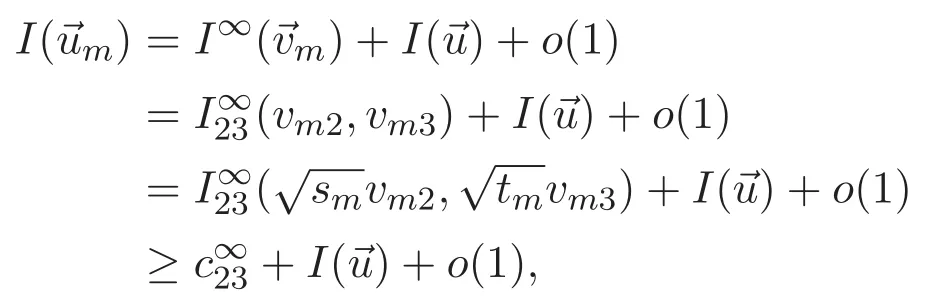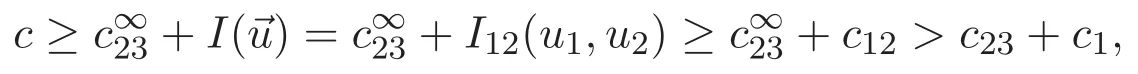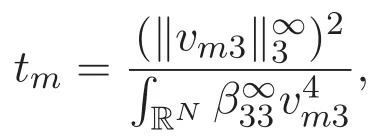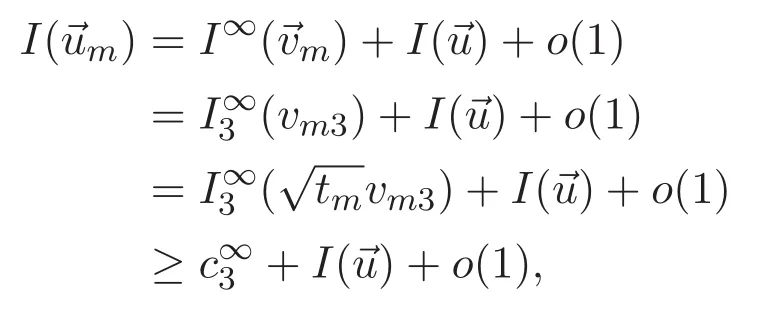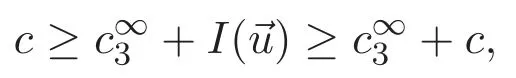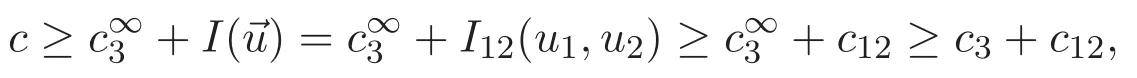Ground states of a system of three Schr?dinger equations
Chen Xinyan,Liu Haidong,Liu Zhaoli
(1.School of Mathematical Sciences,Capital Normal University,Beijing 100048,China;2.Institute of Mathematics,Jiaxing University,Zhejiang 314001,China)
(Communicated by Guo Zhenhua)
Abstract:In this paper we consider a system of three coupled nonlinear Schr?dinger equations,which comes from nonlinear optics and Bose-Einstein condensates.We deal with two types:systems with periodic potentials,and systems with trapping potentials.Using the generalized Nehari manifold and delicate energy estimates,we establish the existence of a positive ground state for either type provided that the interacting potentials are suitably small.
Keywords:ground state,nonlinear Schr?dinger system,variational methods
1 Introduction
In this paper we consider the nonlinear Schr?dinger system of three equations
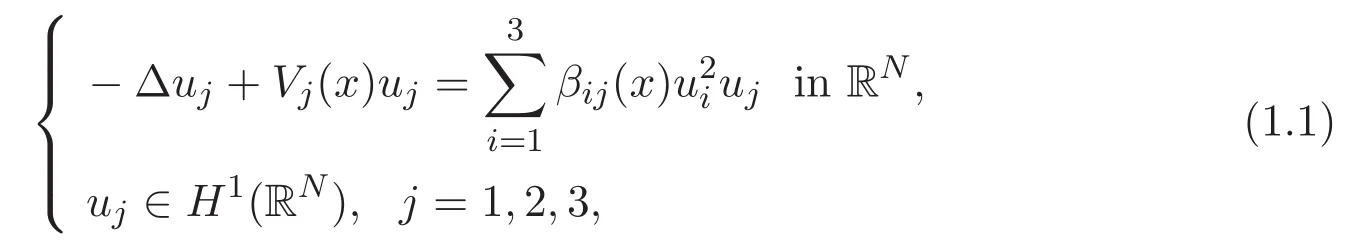

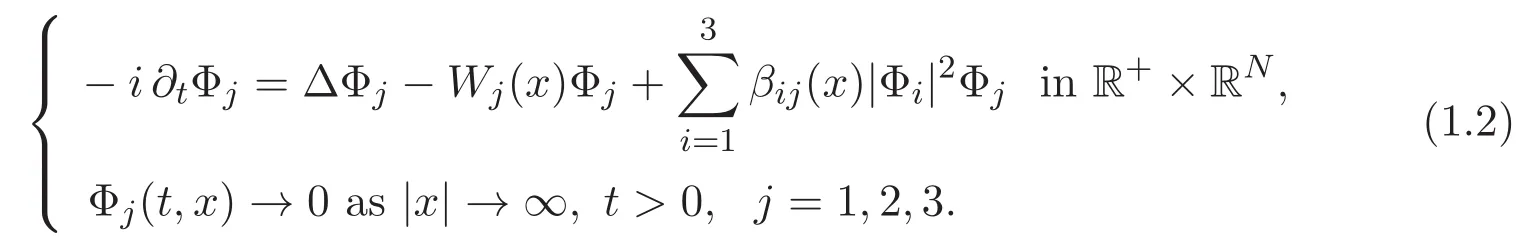
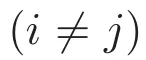
A solution(u1,u2,u3)of(1.1)is said to be nontrivial if all the three components are nonzero.Only nontrivial solutions are of physical interest since(1.1)describes wave functions of three species and each component stands for a wave function of a species.Existence of nontrivial solutions is mathematically challenging since there is no standard technique to distinguish them from semitrivial solutions which we mean solutions with exactly one or two components being nonzero.In this paper,we are interested in the existence of a ground state of(1.1)which,by definition,we mean a nontrivial solution which has the least energy among all nontrivial solutions.
Nonlinear Schr?dinger system has attracted much attention in the last twenty years.While most of the existing papers have been devoted to the existence,multiplicity and quantitative properties of nontrivial solutions for systems of two coupled Schr?dinger equations in various different parameter regimes of nonlinear couplings(see References[7-19]),very few papers focus on systems of k(k≥3)coupled equations(see References[7],[13],[20-26]).The reason is that many techniques which can be applied to systems of two coupled equations are not easy to be adapted to systems of at least three coupled equations.It has been turned out that systems of at least three coupled equations are much more complicated than systems of two coupled equations.
The first motivation of the present paper is to generalize a result in Reference[27]for a system of two coupled equations to system(1.1).The authors of Reference[27]proved that,among other things,the system of two coupled equations
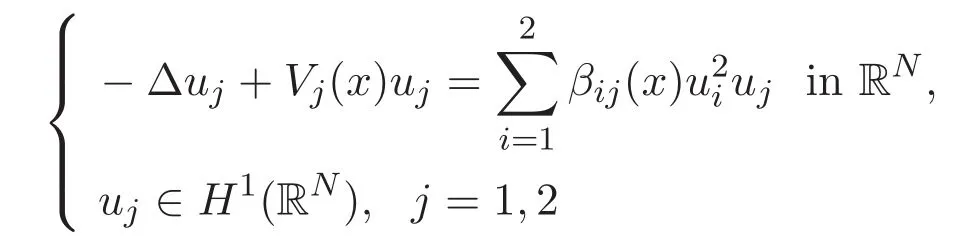
has a positive ground state if β12is suitably small,assuming that Vjand βijare either periodic potentials or trapping potentials.We shall extend this result to(1.1).
Until now,almost all the studies in the literature have been conducted on systems with constant coefficients,that is,systems with Vjand βijbeing all constants.All the above mentioned papers except Reference[27]concern systems with constant coefficients.To exhibit a new existence result for a system of three equations with nonconstant potentials is the second motivation of our paper.
We assume that Vjand βijare either periodic potentials or trapping potentials.Note that constants Vjand βijare both periodic potentials and trapping potentials.The precise assumptions on Vjand βijare as follows.
(A1)For i,j=1,2,3,Vjand βijare positive functions and are τk-periodic in xk,τk>0,k=1,···,N.

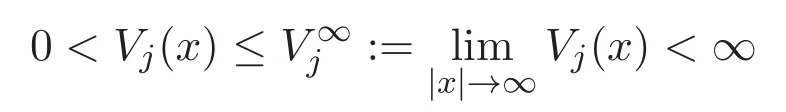
and
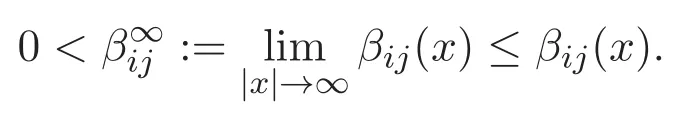
It is known that,under the assumption(A1)or(A2),the scalar equation
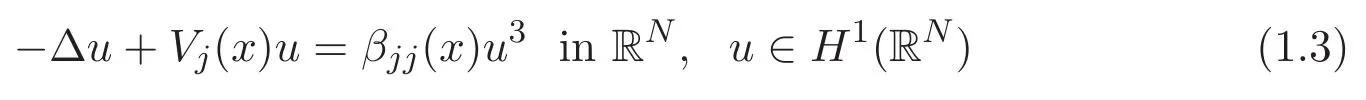
possesses a positive ground state.Let wjbe a positive ground state of(1.3).It is clear that the infimum
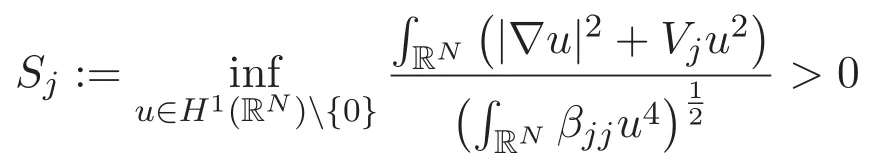
is attained by wjand
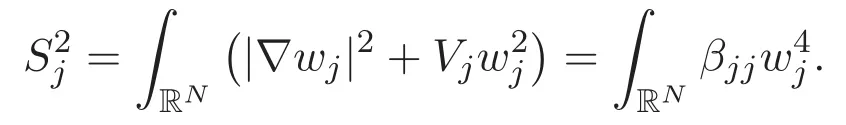
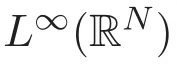
(A3)For 1≤i (A4)For 1≤i The first main result of this paper is for the periodic case and is as follows. Theorem 1.1 If(A1)and(A3)hold,then system(1.1)has a positive ground state. This theorem has an immediate corollary. Corollary 1.1 If(A4)holds,then the system has a positive ground state. Our second theorem is for the trapping potential case. Theorem 1.2 If(A2),(A3)and(A4)hold,then system(1.1)has a positive ground state. Note that Corollary 1.1 is also an immediate consequence of Theorem 1.2.Theorems 1.1 and 1.2 coincide if in particular Vjand βijare constants.However,our proof of Theorem 1.2 is based on Corollary 1.1. The paper is organized as follows.We prove some useful lemmas in Section 2.Section 3 is devoted to the proof of Theorem 1.1 while Section 4 is devoted to the proof of Theorem 1.2. We introduce some notations first.Throughout this paper,we shall use the equivalent norms The symbols?and→denote the weak and strong convergence,respectively,and o(1)stands for a quantity tending to 0. Solutions of system(1.1)correspond to critical points of the functional Clearly,nontrivial solutions of system(1.1)are contained in the generalized Nehari manifold where Since we are interested in selecting nontrivial solutions from all solutions of(1.1),we need to avoid solutions with only one or only two components being nonzero which are in fact solutions of scalar equations and systems of two equations.The functional and the Nehari manifold associated with the scalar equation(1.3)is denoted by Ijand Njrespectively,j=1,2,3,i.e., and For 1≤i That is and Define which are the least energy of(1.3),(2.1)and(1.1)respectively.To prove Theorems 1.1 and 1.2,we need to build suitable relationships among these quantities. In what follows,we always assume that either the assumptions of Theorem 1.1 or the assumptions of Theorem 1.2 hold.We recall that,under the assumption(A1)or(A2),wjis a positive ground state of(1.3).It is easy to see that where Sjis the infimum defined in the introduction. Lemma 2.1 For 1≤i Proof It follows from(A3)that Since the function is strictly increasing in η∈(0,min{Si,Sj}),we have The proof is complete. Remark 2.1 Let 1≤i Lemma 2.2 If(Ui,Uj)is a ground state of system(2.1),then Proof By Lemmas 3.1 and 3.2 in Reference[27],we have Then Lemma 2.1 yields Similarly, The proof is complete. Lemma 2.3 For 1≤i Proof Letting(Ui,Uj)be a positive ground state of(2.1),we have Denote Using(A3)we see that This inequality combined with(2.2)and(2.3)implies ci Since we deduce from Lemma 3.1 in Reference[27]that The proof is complete. Lemma 2.4 c We shall only prove c and To prove Lemma 2.4,we need to show that the linear system has a solution(r,s,t)with three positive components,where Set and Lemma 2.5We have Proof This is just direct and elementary computation. Lemma 2.6 The following inequalities hold: Proof In view of Remark 1.1 one easily obtains the first three inequalities.We estimate b2+b3as Then,by(A3)and Remark 1.1, and The proof is complete. Lemma 2.7 ?>0,?j>0 for j=1,2,3,and Proof As a consequence of Lemma 2.5 and the first three inequalities in Lemma 2.6,we have By Lemma 2.5 and the first and the fourth inequalities in Lemma 2.6,we see that The following estimate for?2uses Lemma 2.5 and the first,the second,the fourth,and the sixth inequalities in Lemma 2.6 In the same way,we also have?3>0.To prove the last inequality of the lemma,observe from Lemma 2.5 that Then using the first,the fourth,the fifth and the sixth inequalities in Lemma 2.6 yields The proof is complete. We now prove Lemma 2.4. Proof of Lemma 2.4 By Lemma 2.7,(2.4)has a unique solution(r,s,t)with Then and the infimum c=infNI can be estimated as We then use Lemma 2.7 again to obtain c Proof This is a direct consequence of Lemmas 2.3 and 2.4. then and ProofDenote that is By(A3),we see that and Then The estimate of the determinant is as follows The proof is complete. In this section we prove the first main result. where where We claim that It remains to prove(3.2).Since,by Lemma 2.9, the P.L.Lions lemma implies that,for any r>0, from which it follows Passing to a subsequence,we may assume that the limits exist.We shall prove that It remains to prove(3.4).We use an argument of contradiction and assume that(3.4)is false.Then we have the following three cases. Case 1:γj>0 for j=1,2,3.In this case,we consider the linear system where By(3.3),the linear system(3.5)can be rewritten as We see from the arguments in the proof of Lemma 2.9 that,for large m, Then the linear system(3.5)has a unique solution(rm,sm,tm)and Consider the linear system where By(3.6),the linear system(3.7)can be rewritten as Since γ2>0 and γ3>0,we have for large m.Then the linear system(3.7)has a unique solution(sm,tm)and sm=1+o(1),tm=1+o(1). which is impossible.In the case where u2=u3=0,we have which also contradicts Lemma 2.4. which is impossible.In the case where u3=0,we have which contradicts Lemma 2.4. In each case we have come to a contradiction.This proves(3.4)and(3.2)in turn.The proof is complete. In the trapping potential case,we need to consider the limit systems of(1.1),(1.3)and(2.1).The functional associated with(1.4)is and the generalized Nehari manifold is given by where The functional and the Nehari manifold associated with the scalar equation respectively. Define which are the least energy of(4.1),(4.2)and(1.4)respectively. Proof The method of the proof of the first three inequalities is standard(see Reference[27]).Now we use the idea in Reference[27]to prove that if at least one of the nine functions Vjand βijis not constant then c Note that(u1,u2,u3)satisfies By the assumption(A2)we see that,for i,j=1,2,3, For simplicity of symbols,we denote and By(A2),we see that where Then Note that After a lengthy but elementary calculation,we expand Ayas where high order terms mean the summation of the square,the cubic and the fourth order terms of χijand ψj.By(A2),if at least one of the nine functions Vj(j=1,2,3)and βij(1 ≤i≤j≤3)is not constant then Similar to the proof of?y>0,we have According to(4.4),if|y|is sufficiently large,then each of χij(y)and|ψj(y)|is sufficiently small.Hence we arrive at c∞>c.The proof is complete. We are in a position to prove the second main result. from which it follows Assume up to a subsequence that the limits Therefore,it remains to prove We assume,by contradiction,that(4.7)is false and we divide the discussion into three cases. where By(4.6),the linear system(4.8)can be rewritten as We see from arguments in the proof of Lemma 2.9 that,for large m, Then the linear system(4.8)has a unique solution(rm,sm,tm)and Consider the linear system where By(4.9),the linear system(4.10)can be rewritten as for large m.Then the linear system(4.10)has a unique solution(sm,tm)and which also contradicts Lemma 2.4. which is impossible.In the case where u3=0,we use Lemma 4.1 to deduce which contradicts Lemma 2.4. In each case we have come to a contradiction.The proof is complete.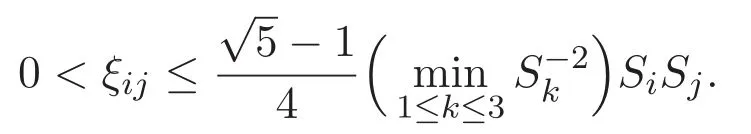
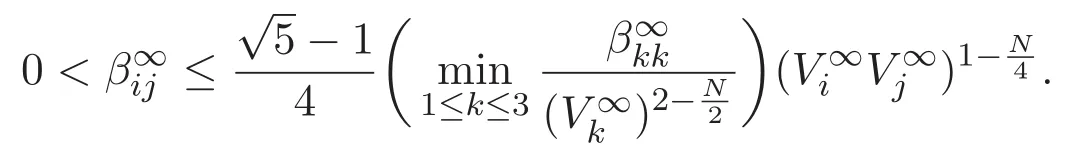
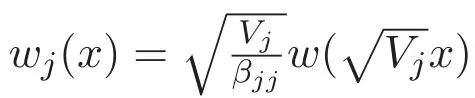
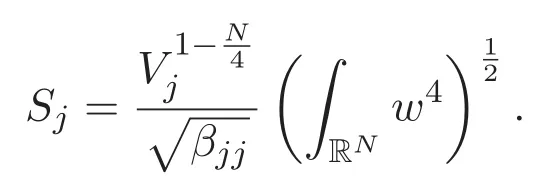
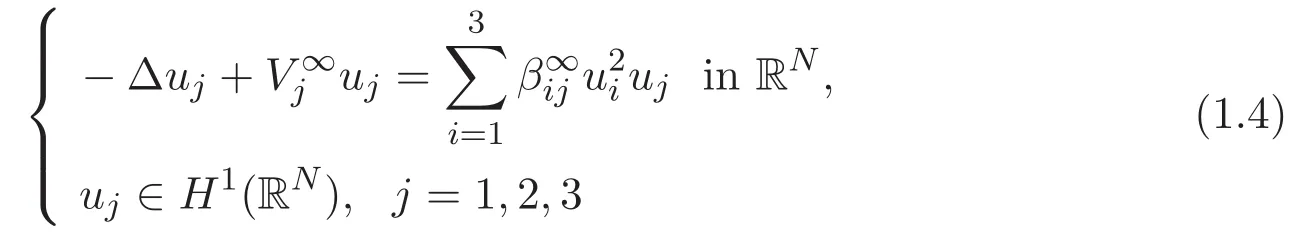
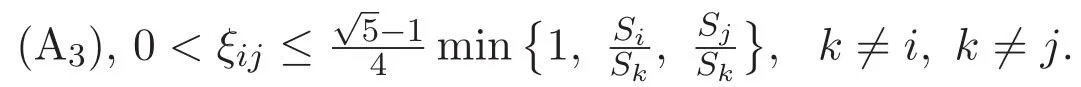
2 Preliminaries
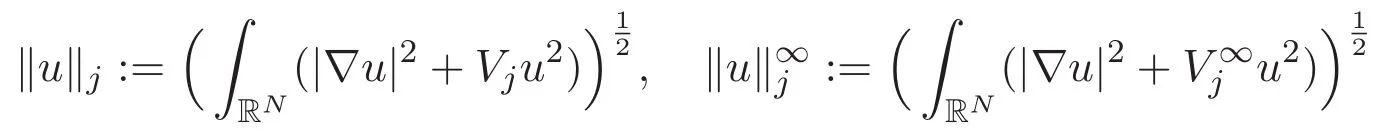
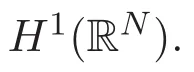
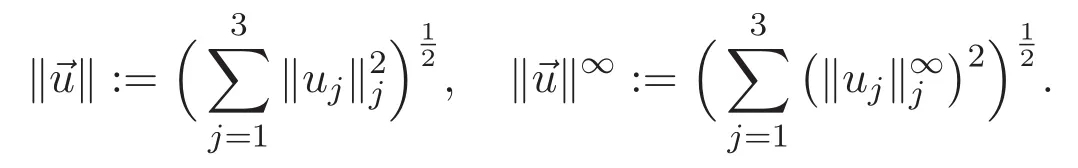
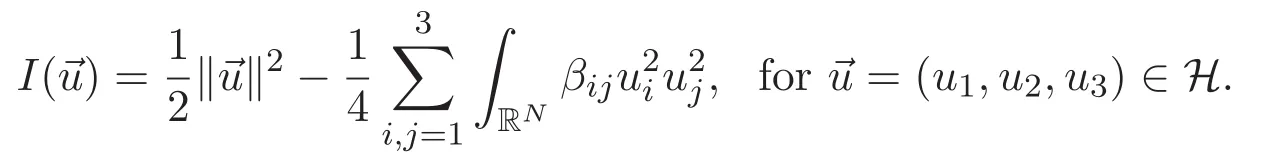
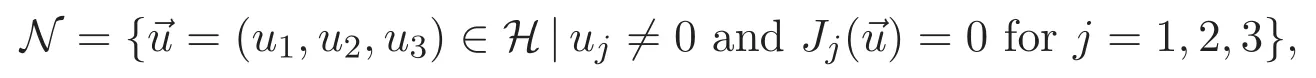
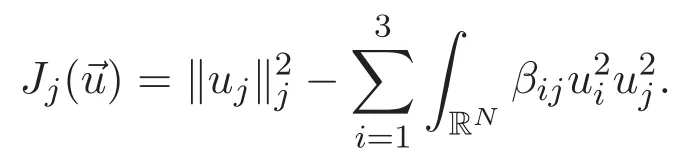

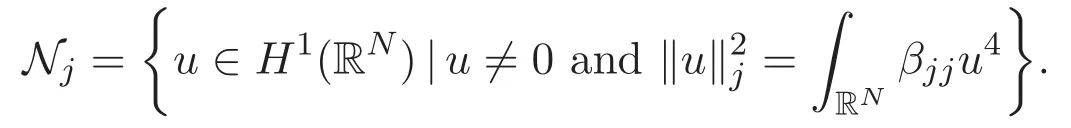
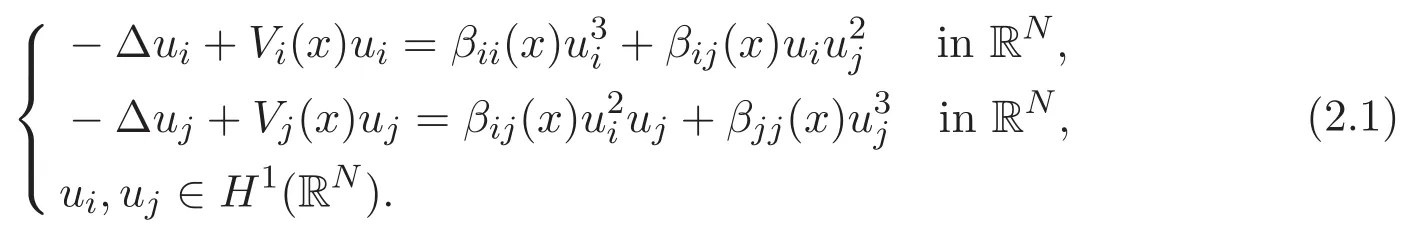
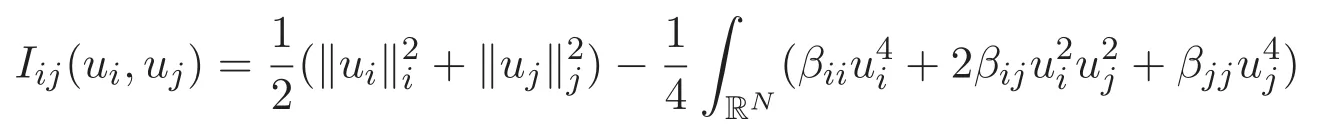
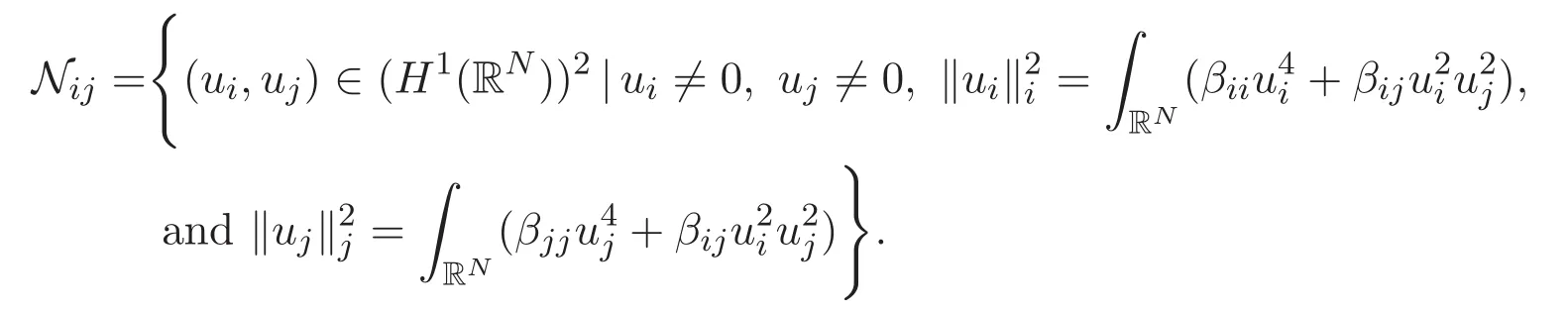
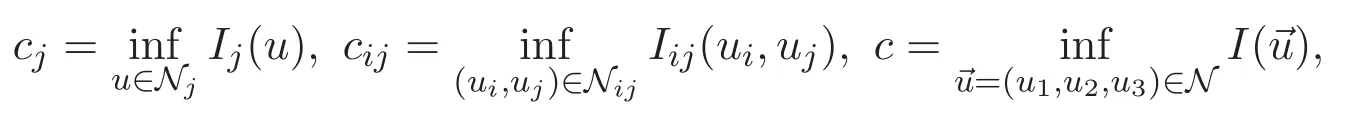
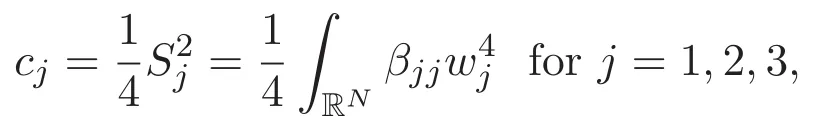
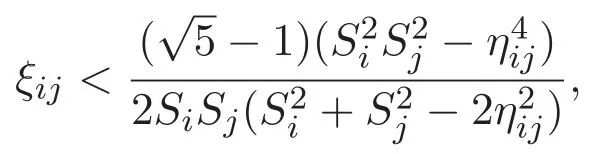
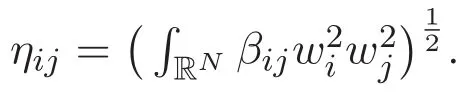
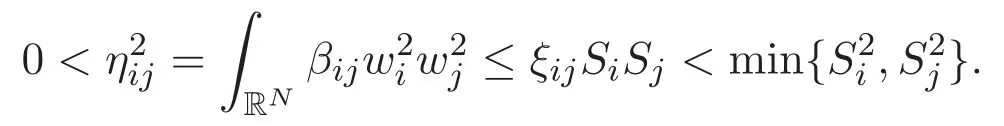



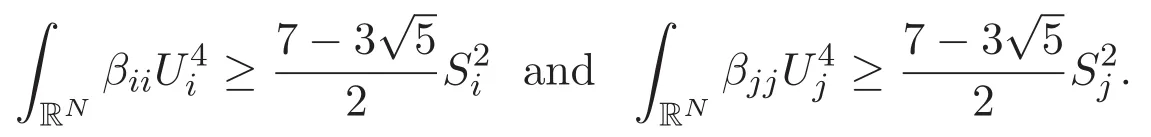
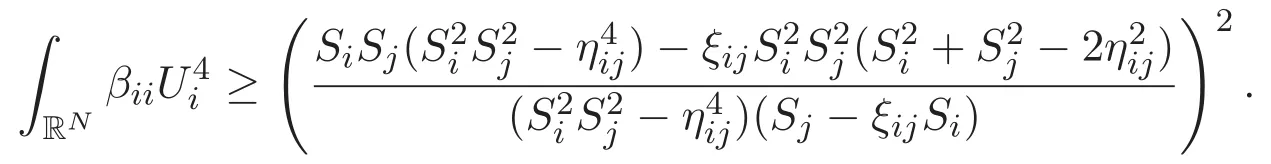
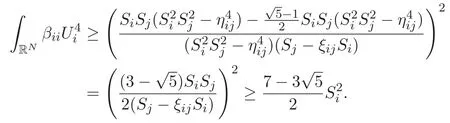
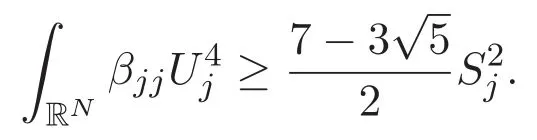
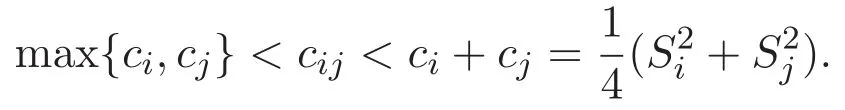
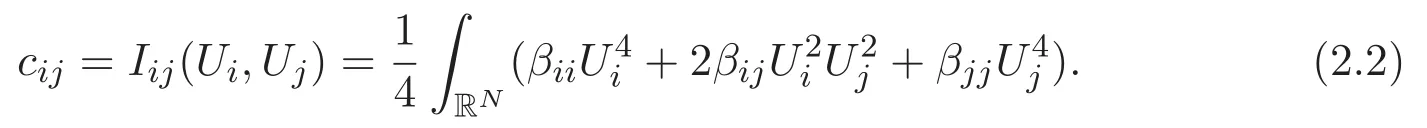
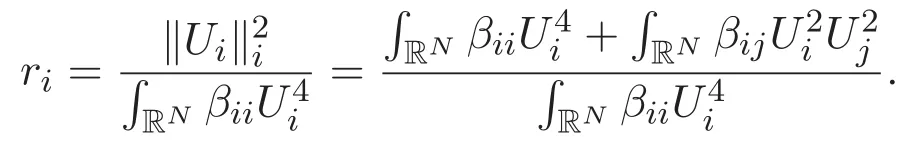
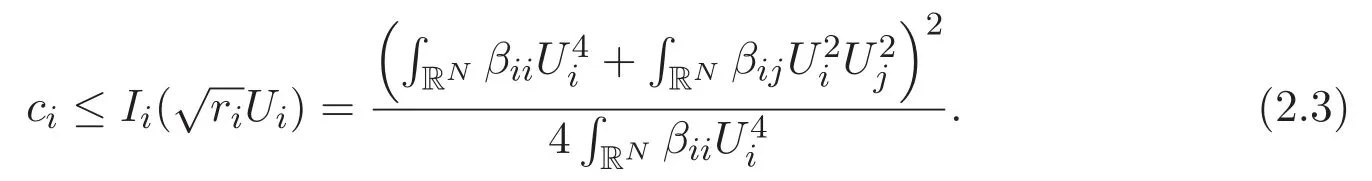
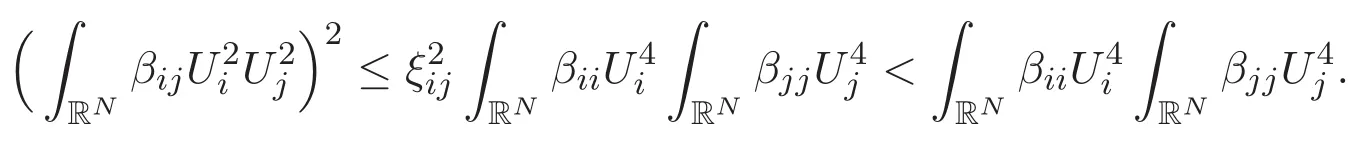
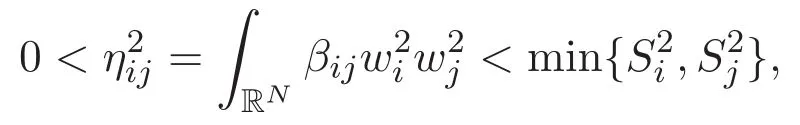
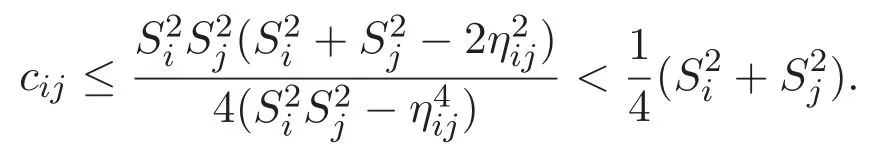
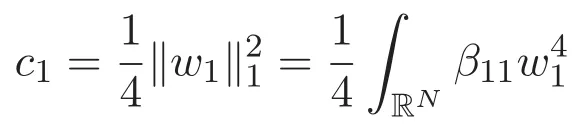
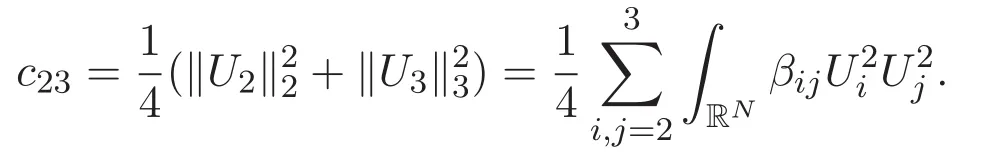
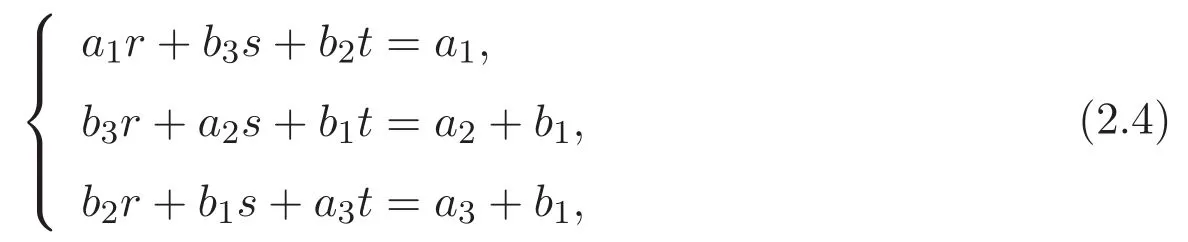
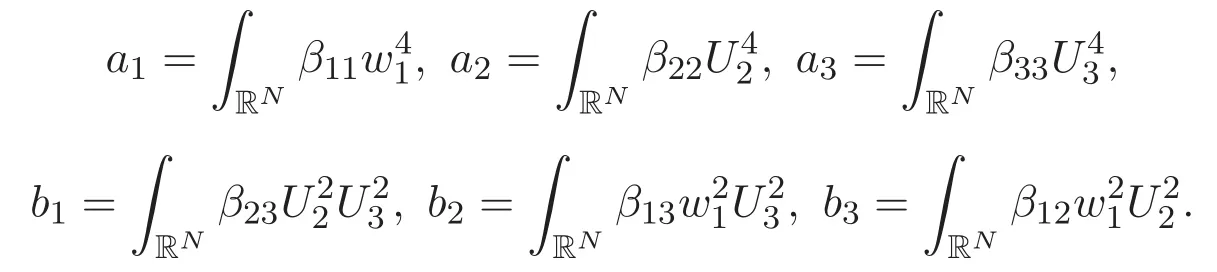
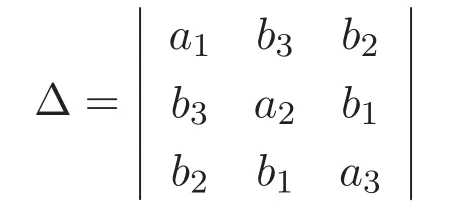
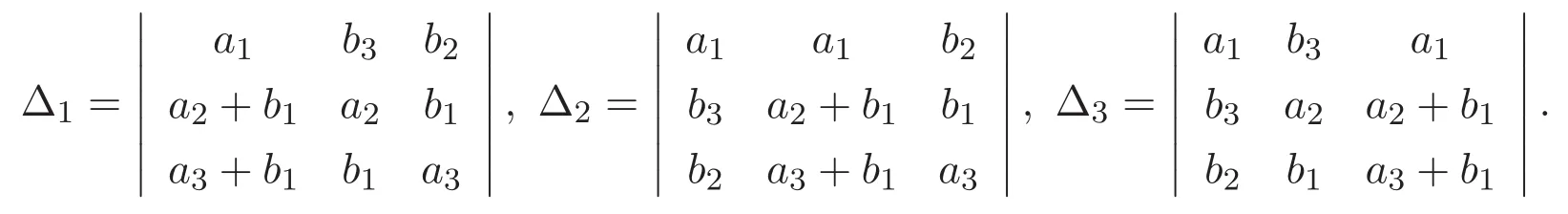
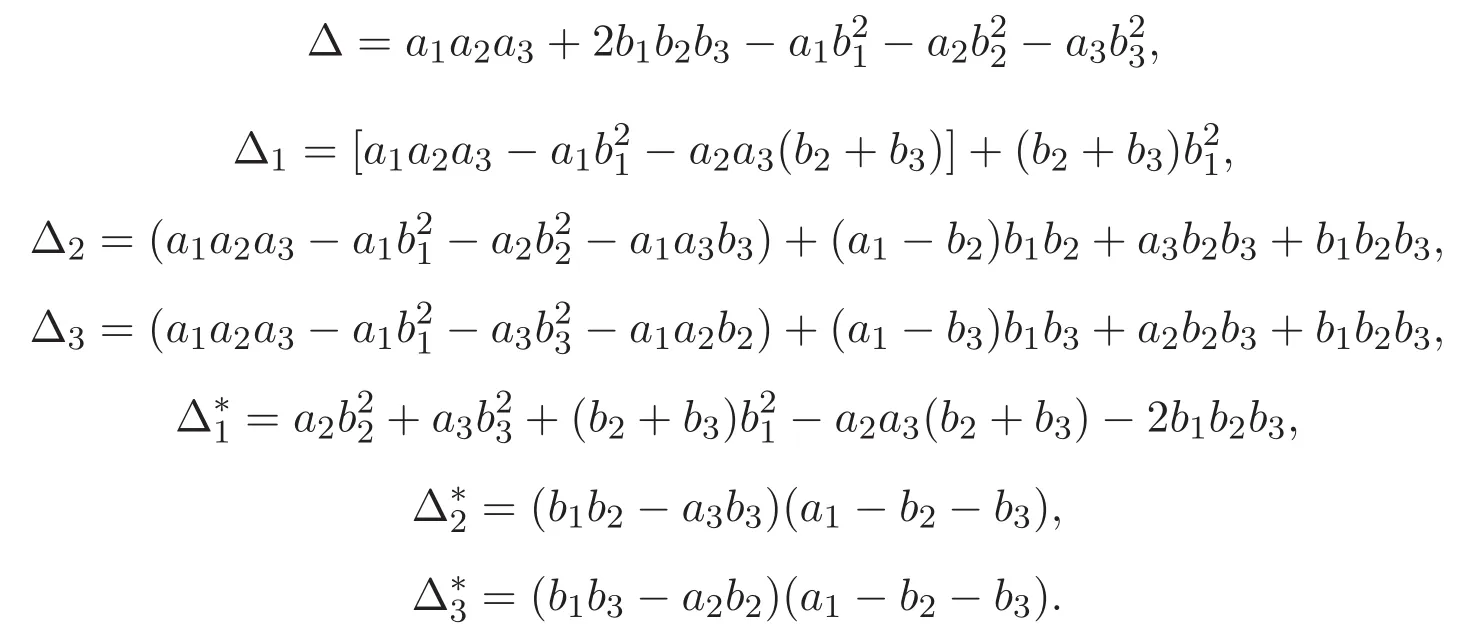
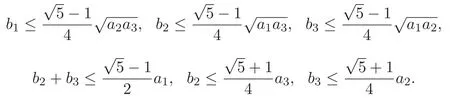
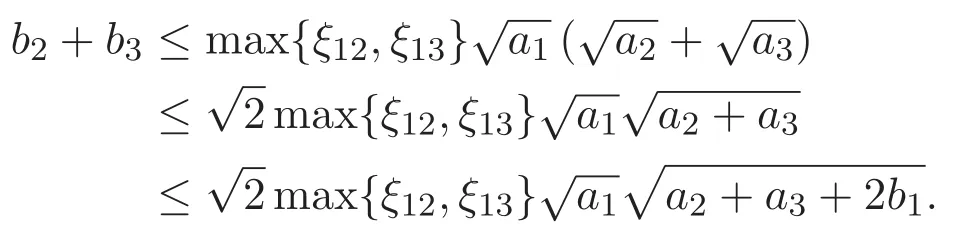
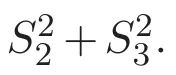
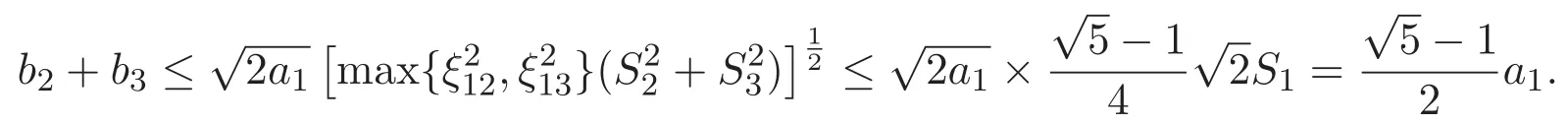
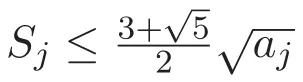
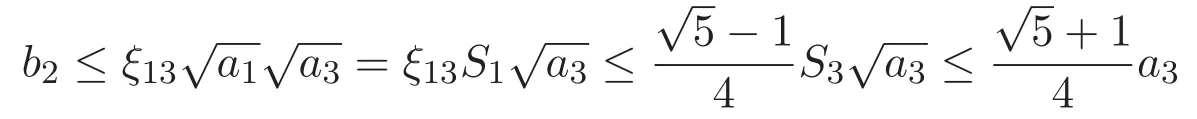
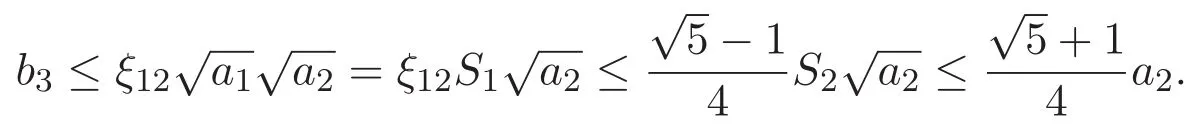
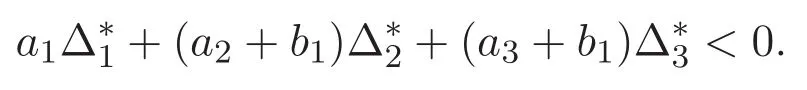
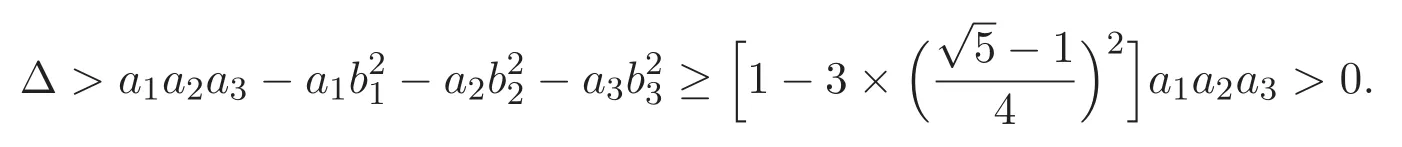
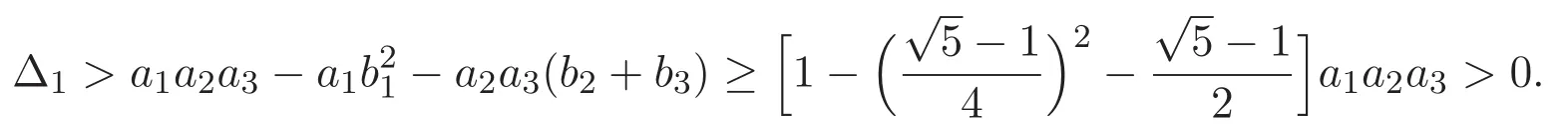
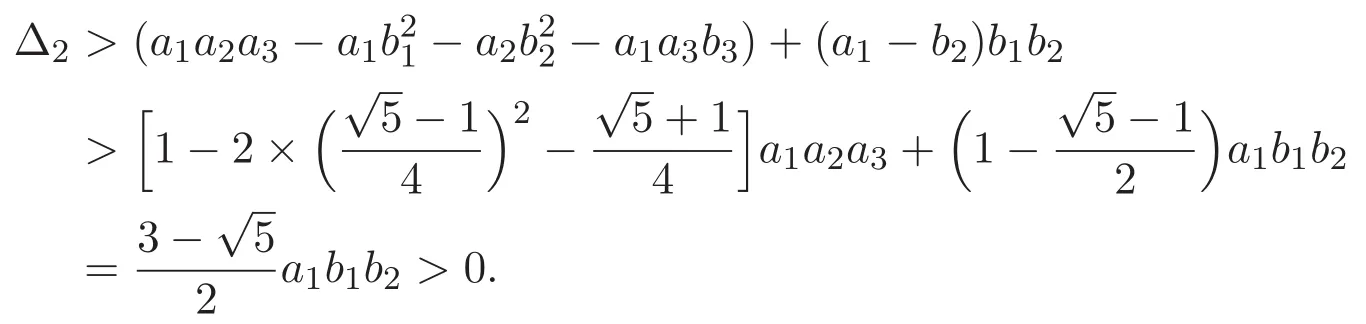
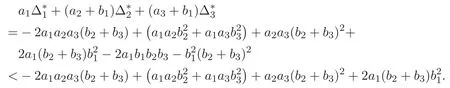
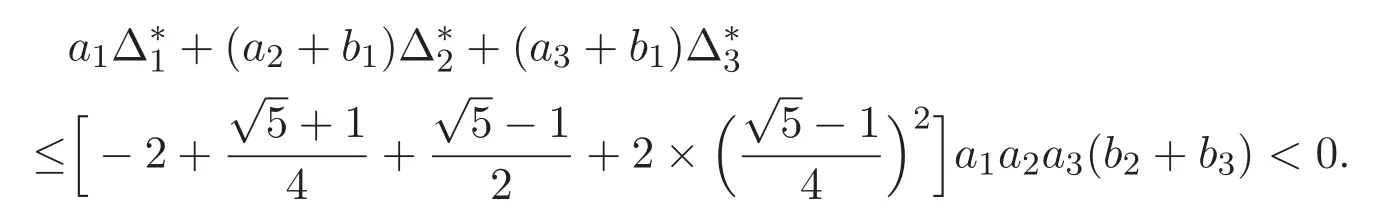
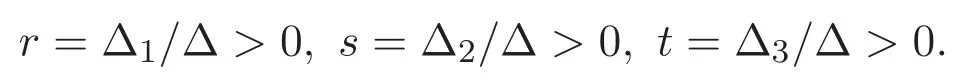
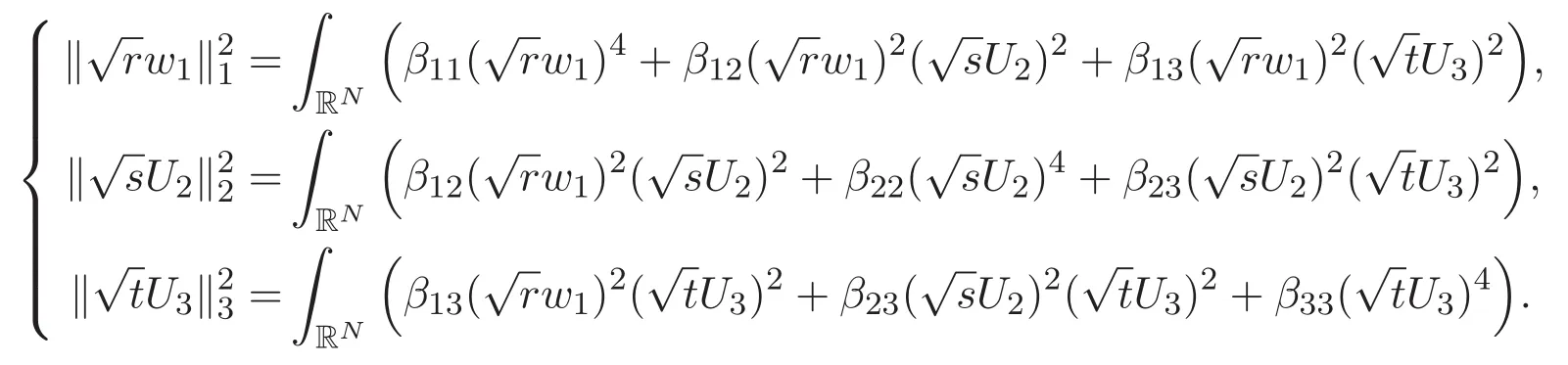
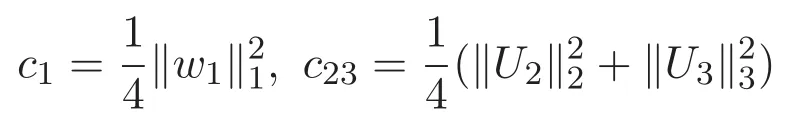
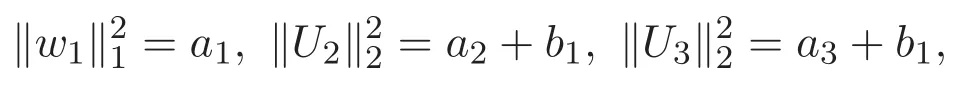
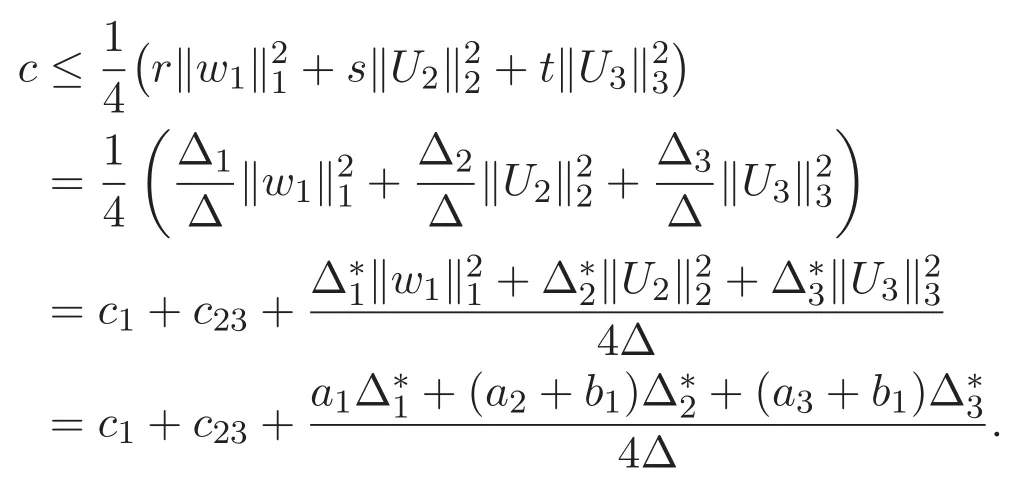
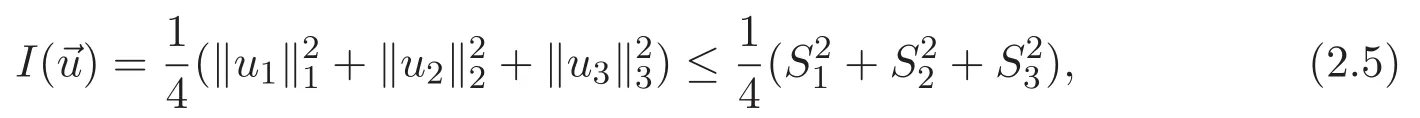
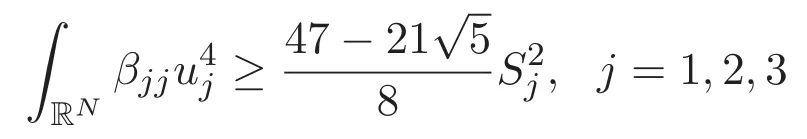
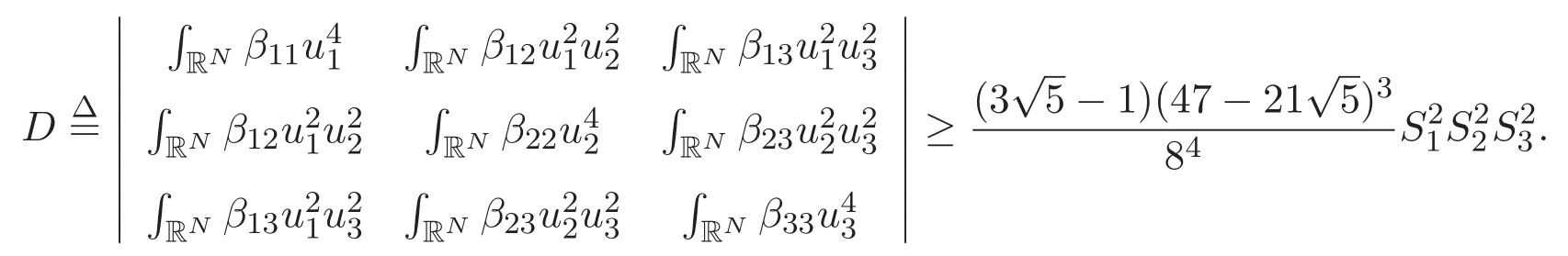
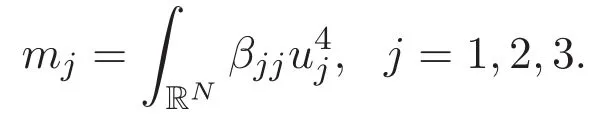
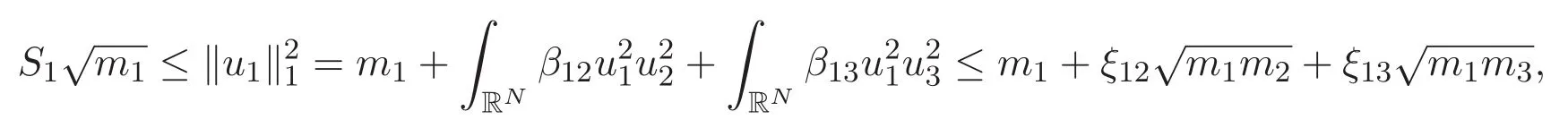
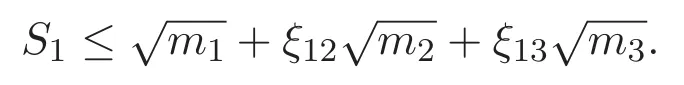

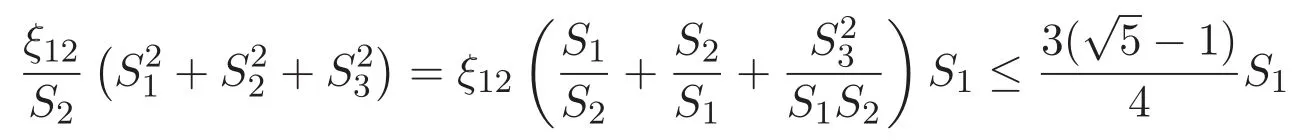
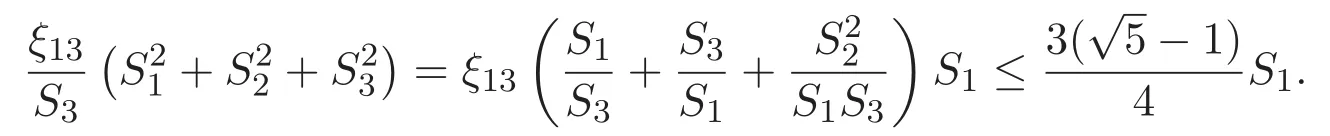
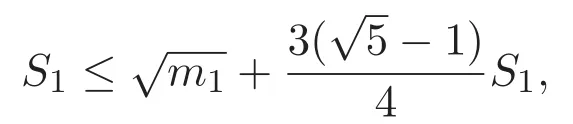
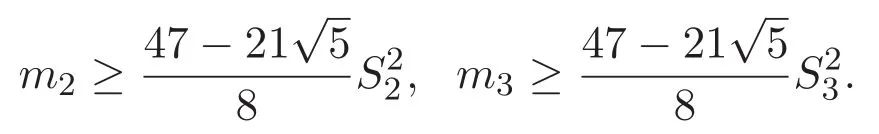
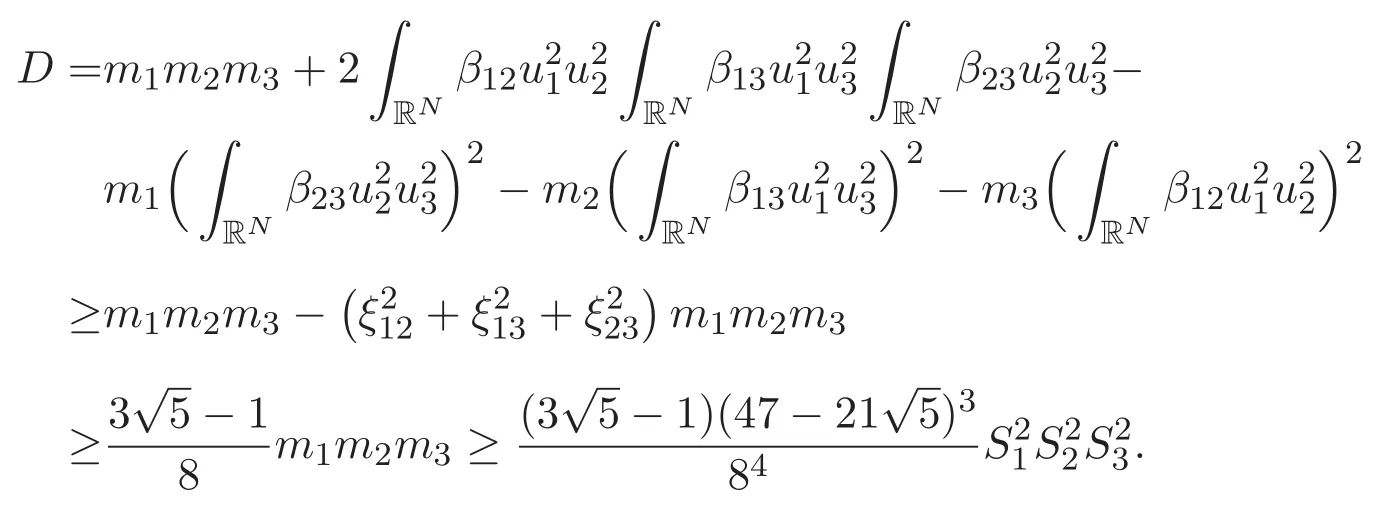
3 Proof of Theorem 1.1


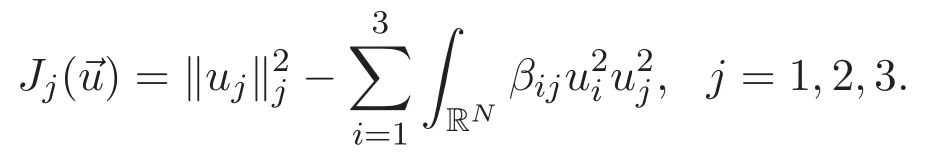
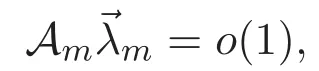
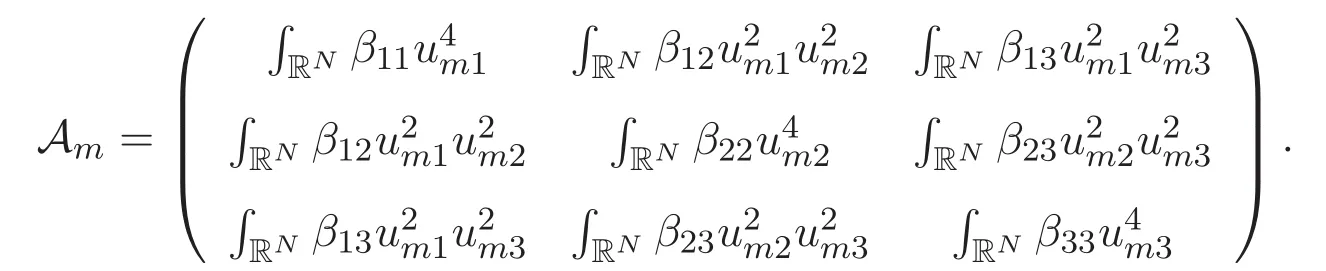
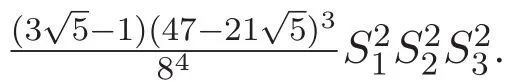
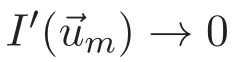

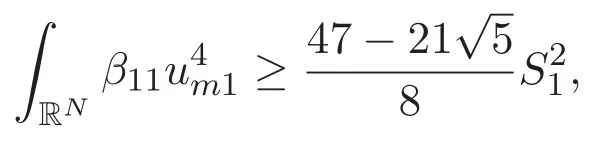
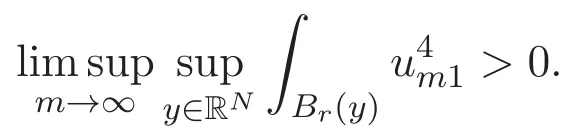
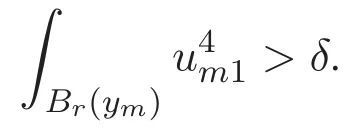

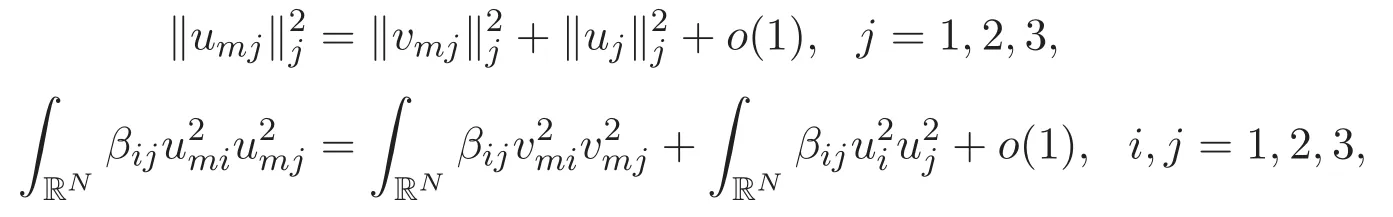
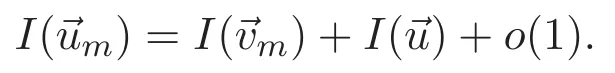
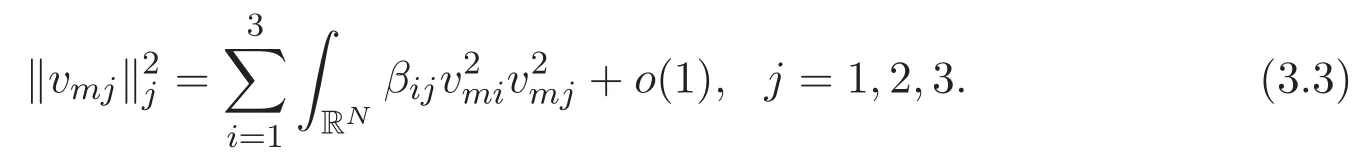
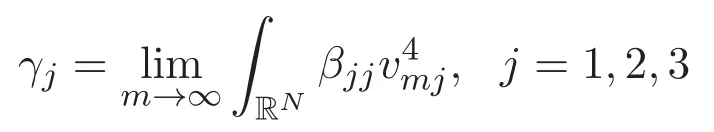

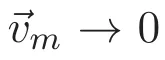
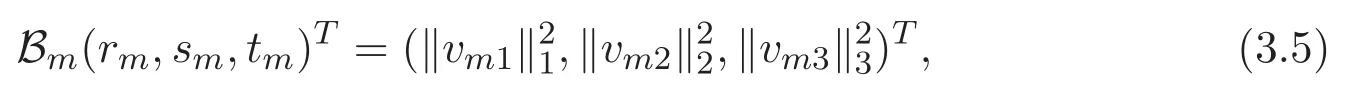

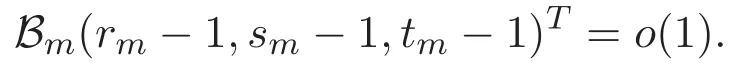
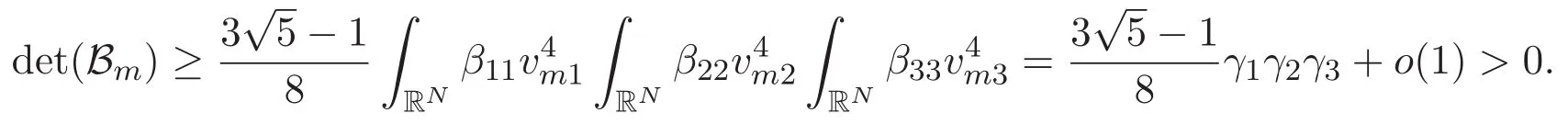
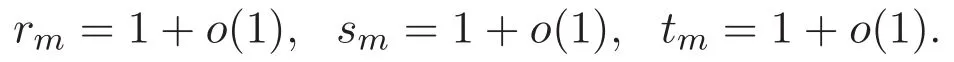
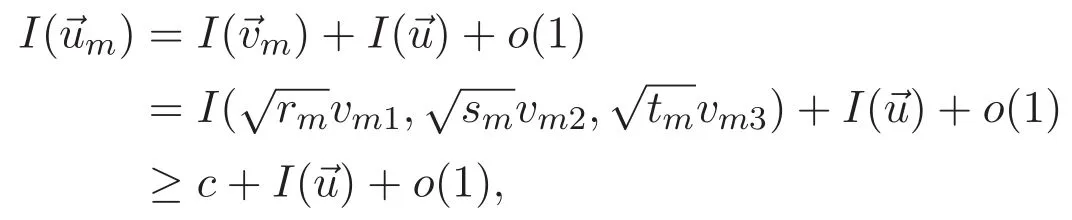
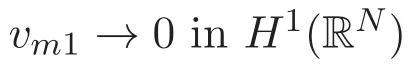
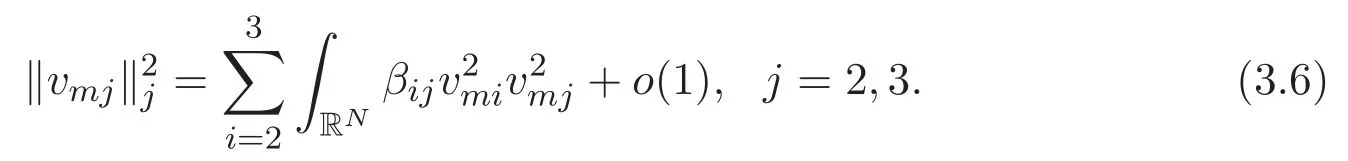
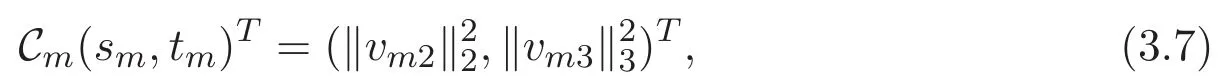
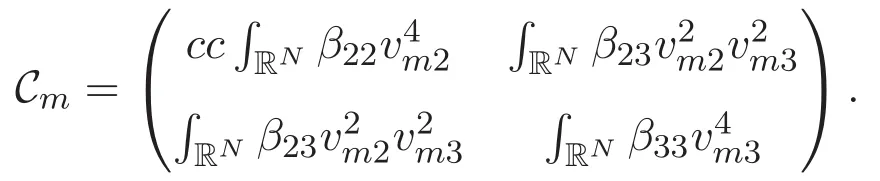
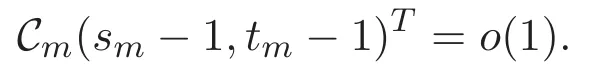
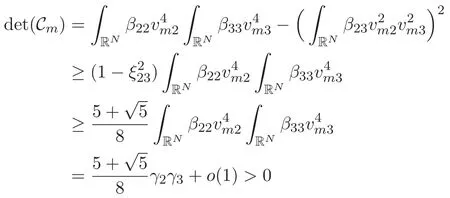
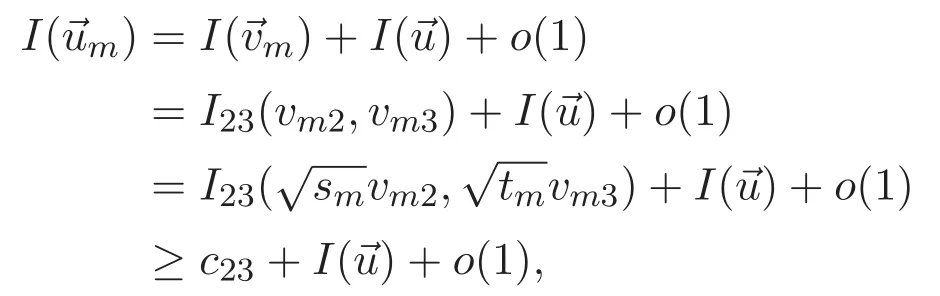
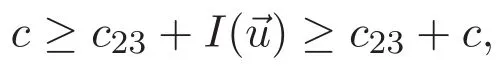
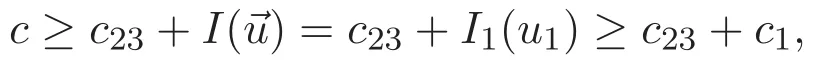
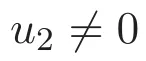
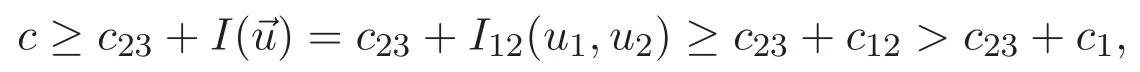
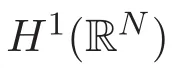
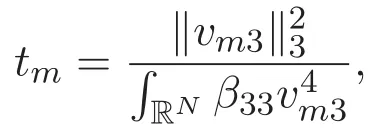
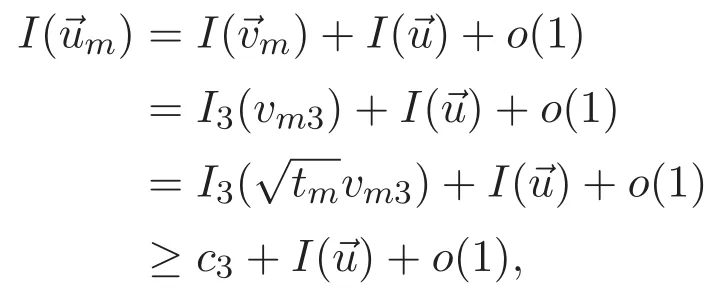

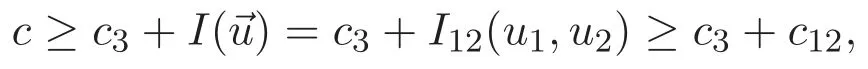
4 Proof of Theorem 1.2