一種無人機中繼系統調度的優化方法

楊 楠

（佳木斯大學信息電子技術學院 黑龍江 佳木斯 154000）

1 引言

隨著全球變暖趨勢的不斷加劇，各地環境受到嚴重影響，以森林火災等自然災害為例，近年來，澳大利亞和美國等許多地方被大規模的野火侵蝕，對當地安全和全球生態造成了巨大破壞[1]。當災難發生時，由于基站等設備損毀導致平常的通信手段失效，需要緊急應對措施實現對災難點的通信，無人機中繼系統具有空中作業覆蓋面廣、操作靈活方便、精度高等優點，用于野火隱患排查，既能有效降低作業難度、成本和安全威脅，又能保證作業效率和質量，有效降低火災發生的概率。

2 無人機中繼系統的優化

2.1 無人機中繼系統的部署優化

針對無人機中繼廣播通信系統性能優化問題，在給定合理中繼率的基礎上，找出最佳信息傳輸速率。利用所在位置找出最好的d，從而改善中繼系統的中繼效率，考慮無人機性能、火災強度、人口信息等因素，無人機載中繼通信平臺至地面通信終端為單點對多點通信方式，采用基于時分復用方式傳輸數據[2]，地面通信終端至無人機通信平臺為多點對一點通信方式，采用TDMA多址接入方式傳輸數據[3]。該系統將通信有效覆蓋面積大幅度提高；同時使在復雜地形中進行應急通信變得更有效率和便捷，實現多址鏈路在非視距的情況下的正常通信。

假設無人機載中繼通信平臺與地面通信終端距離較遠，不存在無人機載中繼通信平臺到各個用戶節點的直達通信鏈路，則必須通過無人機的中繼才能夠實現地面通信終端節點（源節點）與各個中繼節點的廣播通信。

在發生山火的情況下，中繼無人機可以在不同的地形和火災條件下進行遙感監測，使地面指揮部隊能夠做出最佳的戰略部署，保證消防人員的安全。以澳大利亞維多利亞州發生的山火為例。從美國宇航局衛星儀器MODISC6和VIIRS375M中，收集了澳大利亞火災數據集，選取了能覆蓋維多利亞的50個地點的經緯度，火災強度高，火災發生頻率高，以火災事件的大小和發生頻率為參數，計算50個位置之間的距離，并生成鄰接矩陣。使用MATLAB仿真的維多利亞火災地點模擬圖，其中火災主要分布在維多利亞州東南部山林密集，人口稠密的地區。

基于對火災地形的模擬，將地面通信終端編號為1，無人機載中繼通信平臺依次編號為2、3至52。由于我們選擇的數據是50個位置的經度和緯度計算這兩點之間的實際距離。

假設甲、乙兩點的地理坐標分別為( x1,y1)，( x2,y2)，以地球中心為坐標原點稱為d0，半徑R =6370。大圓經過兩點A和B的小弧長，就是兩點之間的實際距離。這兩點的直角坐標是：

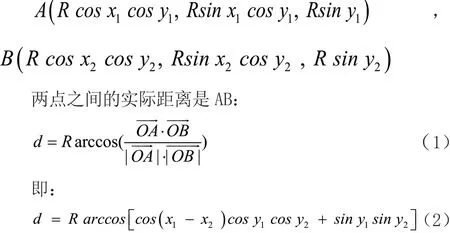
距離模型基于Matlab D = (dij)52×52，其中 dij表示i,j兩點之間的距離，i, j= 1,2,… 5 2.。

2.1.1 空間解決方案

解空間S可以表示為?的所有固定的起點和終點的循環排列的集合，即S =?，{2，3，...，51}的循環排列，其中這些環路中的每一個代表由中繼無人機偵察50個火災現場形成的環路，πi= j表示第j個中繼無人機探測到第一個起火點。通過多次實驗，我們選擇了一個較好的初始解為120。

2.1.2 目標函數

代價函數，也稱目標函數[4]，表示為中繼無人機在監測所有火場時的路徑長度。讓這個函數表示為：

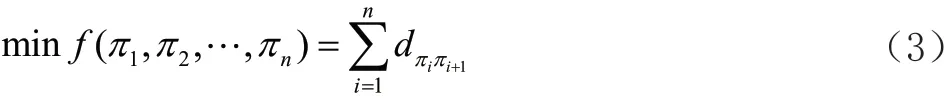
最后，通過模擬退火算法[5]得到中繼無人機飛行的最短路徑，見圖1，該路徑上的中繼無人機可以監控和覆蓋所有火災位置。中心位置黑點標注為MATLAB仿真所得到的地面移動終端即源節點所在位置。

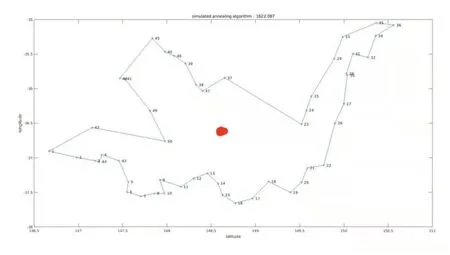
圖1 無人機中繼平臺的最佳部署位置

2.2 無人機多中繼節點的分配

在基于模擬退火算法模擬中繼無人機的最佳飛行路徑后，本文綜合考慮了維多利亞地形和通信任務要求以及中繼無人機性能，建立了最小成本和最大流量模型，以確保維多利亞火災情況的完全覆蓋和監控，同時最小化成本預算。

最小費用最大流模型的思想是在邊容量和邊費用有限的流網絡中，尋找從一個節點到另一個節點的費用最大和最小的流。根據最小費用最大流模型的原理，假設中繼無人機的速度為20 km/h，給定一個流網絡G=(V,E,L,U,D)，其中V是節點集，E是邊集，L是(Vi,Vj)邊容量的下限集，U是(vi,vj)容量的上限集。對于每條邊，(vi,vj)被賦予一個實數fij，它被稱為邊上的流，(vi,vj)。圖2顯示了任意兩個節點dij之間的距離，表示對應側的容量值。

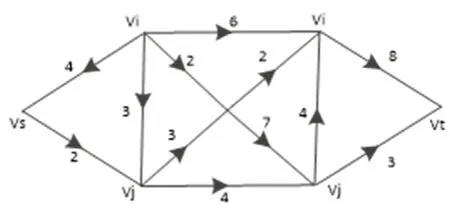
圖2 模型網絡示意圖

即0 ＜dij＜∞；每一方所需無人機的成本是wij；f的流量成本是從源點s經過到匯點t的各邊無人機的成本之和；每一邊的流都被中繼無人機所覆蓋。從源點到宿點t的流量f通過節點i j v v，以滿足要求：0 ≤fij＜dij，對于所有中間節點vi∈v- {s,t} ，它滿足：。所以f是可行流，這個中繼無人機飛行網是可行域。

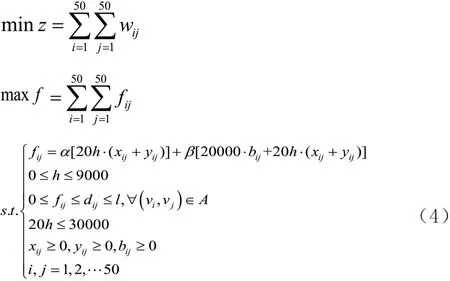
將中繼無人機的位置為因變量，考慮維多利亞的特征屬性，如區域類型（農村地區、郊區、城市地區）、海拔、火焰輻射頻率、人口數量、各區域占地面積等，設為自變量。選擇了維多利亞的94個地點進行仿真，基于獲得了50個關于中繼無人機位置的數據樣本。數據樣本被隨機分為訓練集和驗證集，比率為4：1。在每個實驗中，使用40個數據樣本來進行初步的邏輯回歸和訓練參數，其余使用10個數據樣本來驗證模型的預測準確性。使用向后消除方法進行邏輯回歸預測，設0.5作為分類截止值，為了提高模型的預測能力，我們在邏輯回歸模型中增加了一個方乘項，以執行多次迭代。如果? 0.5y≥ ，則需要在該位置放置無人機載中繼通信平臺；如果?0.5y≤ ，則沒有必要在這個位置使用帶有中繼器的無人機。經過模擬測試，無人機源節點與中繼節點的部署見圖3，考慮火災強度與地形因素的影響，依據上述式子可得到如圖4所示的模擬結果。結果表明，邏輯回歸模型的整體預測精度為96.2%。仿真結果表明該優化方法適應于火災救援。

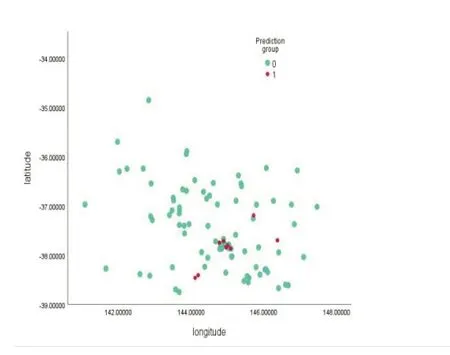
圖3 無人機與中繼器位置的散點圖

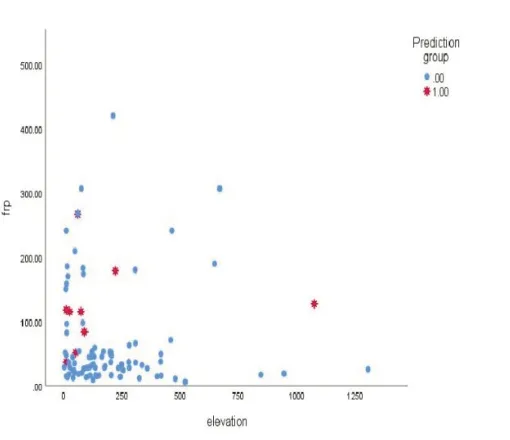
圖4 不同高度和火災強度的無 人機與中繼器的散點圖

3 結語

本文針對四旋翼無人機中繼廣播通信優化問題，給出了一種無人機位置部署優化及其覆蓋區域規劃的聯合優化方法，總結了基于中繼節點平均中斷概率最小化準則的多中繼節點最大通信容量的計算公式，驗證了無人機中繼系統在火災救援中的應用價值。