華南陸地時(shí)變重力觀(guān)測(cè)數(shù)據(jù)質(zhì)量評(píng)估

楊錦玲，陳 石，王林海，盧紅艷，李紅蕾，張 貝

1. 中國(guó)地震局地球物理研究所，北京 100081； 2. 福建省地震局，福建 福州 350003； 3. 北京白家疃國(guó)家地球科學(xué)野外觀(guān)測(cè)研究站，北京 100095

地震、地下水、火山活動(dòng)及各種構(gòu)造運(yùn)動(dòng)和地殼垂直變形等地球動(dòng)力學(xué)過(guò)程，都會(huì)引起一定程度的地球重力場(chǎng)時(shí)空微變化。高精度時(shí)變微重力監(jiān)測(cè)手段常用于觀(guān)測(cè)火山活動(dòng)期間巖漿的運(yùn)動(dòng)[1-2]、地下水儲(chǔ)量變化[3]、油氣庫(kù)含水層[4]及地震危險(xiǎn)性分析[5-9]。與衛(wèi)星重力[10]和海洋重力測(cè)量[11]相比，高精度的地表重力重復(fù)觀(guān)測(cè)具有距離地殼內(nèi)部場(chǎng)源近、觀(guān)測(cè)位置可重復(fù)性強(qiáng)、觀(guān)測(cè)儀器精度高等特點(diǎn)，適用于監(jiān)測(cè)與地殼內(nèi)部場(chǎng)源直接相關(guān)的微重力信號(hào)。

21世紀(jì)，依賴(lài)絕對(duì)重力觀(guān)測(cè)技術(shù)逐漸成熟，為研究重力場(chǎng)時(shí)變信號(hào)提供了更加可靠的時(shí)空基準(zhǔn)[12-16]。例如：2004年至2009年的絕對(duì)和相對(duì)重力聯(lián)合在地表重復(fù)觀(guān)測(cè)到的重力場(chǎng)變化與菲律賓板塊俯沖引起的慢地震相關(guān)[5]；2008年汶川8級(jí)地震和2015年尼泊爾7.8級(jí)地震從絕對(duì)重力重復(fù)測(cè)量結(jié)果提取到震前重力變化信號(hào)[13,15]。但是，由于陸地重力觀(guān)測(cè)特別是時(shí)變重力場(chǎng)信號(hào)的獲取，儀器觀(guān)測(cè)能力限制和場(chǎng)源非唯一性仍是當(dāng)前制約重力方法研究深部介質(zhì)變化的核心難題。重力信號(hào)對(duì)質(zhì)量變化敏感，微伽級(jí)重力數(shù)據(jù)常受到觀(guān)測(cè)方法、儀器精度以及潮汐、環(huán)境、地下水和地表沉降等多種不確定性因素的影響，這也使得陸地重力觀(guān)測(cè)得到的重力場(chǎng)變化存在較多不確定性。

陸地重力觀(guān)測(cè)儀器的不確定性主要來(lái)源于彈簧重力儀的零漂特性和格值系數(shù)[17]。目前，國(guó)內(nèi)外陸地重力觀(guān)測(cè)的主流設(shè)備以L(fǎng)aCoste&Romberg型、CG-5型和Burris型彈簧重力儀為主，但是彈簧型重力儀不具備絕對(duì)觀(guān)測(cè)能力，且CG-5相對(duì)重力儀每天零漂達(dá)50～200×10-8m/s2[18]。對(duì)于較大空間尺度和較長(zhǎng)野外作業(yè)時(shí)間的重力觀(guān)測(cè)，非線(xiàn)性漂移信號(hào)的估計(jì)是提高重力信號(hào)解算精度的關(guān)鍵。文獻(xiàn)[19]提出了一種專(zhuān)用于陸地高精度微重力觀(guān)測(cè)的貝葉斯平差方法，該方法可以對(duì)多儀器聯(lián)合觀(guān)測(cè)自動(dòng)定權(quán)、自適應(yīng)量化重力儀非線(xiàn)性漂移觀(guān)測(cè)誤差，為提高重力平差計(jì)算的精度提供了一種新的解決方案。

華南地區(qū)歷史上中強(qiáng)地震活躍，其近岸海域有6～7級(jí)地震的強(qiáng)震構(gòu)造背景。在華南地區(qū)開(kāi)展高精度的時(shí)變重力觀(guān)測(cè)，對(duì)于識(shí)別潛在強(qiáng)震風(fēng)險(xiǎn)源和研究強(qiáng)震孕育全周期過(guò)程的微重力時(shí)空變化特征具有重要的科學(xué)意義。此外，全面對(duì)華南相對(duì)重力儀器非線(xiàn)性漂移和格值系數(shù)等不確定性因素進(jìn)行量化評(píng)價(jià)，在此前還基本屬于空白，但該工作是進(jìn)一步應(yīng)用地震重力資料分析區(qū)域地震危險(xiǎn)性的基礎(chǔ)，因此本文將采用最新的貝葉斯平差方法，對(duì)華南地區(qū)近年的時(shí)變重力觀(guān)測(cè)資料進(jìn)行評(píng)價(jià)，為后續(xù)資料的分析和應(yīng)用提供科學(xué)依據(jù)。

本文以華南地區(qū)2015年—2018年的時(shí)變重力觀(guān)測(cè)資料為基礎(chǔ)，引入貝葉斯平差技術(shù)，給出華南地區(qū)的重力觀(guān)測(cè)數(shù)據(jù)精度分析，提出通過(guò)重力段差殘差和絕對(duì)重力交叉驗(yàn)證方法來(lái)評(píng)定重力觀(guān)測(cè)資料的精度指標(biāo)方案。第2節(jié)詳細(xì)介紹了華南構(gòu)造背景和時(shí)變重力測(cè)網(wǎng)概況；第3節(jié)給出了研究方法原理；第4節(jié)給出了華南地區(qū)的重力數(shù)據(jù)質(zhì)量評(píng)價(jià)；最后給出了研究結(jié)論。本文研究結(jié)果對(duì)評(píng)價(jià)陸地時(shí)變重力監(jiān)測(cè)數(shù)據(jù)質(zhì)量，更合理和客觀(guān)地解釋重力場(chǎng)變化與場(chǎng)源介質(zhì)屬性之間的關(guān)系，具有較好的參考意義。

1 華南構(gòu)造背景與時(shí)變重力觀(guān)測(cè)網(wǎng)絡(luò)

華南位居太平洋西緣，其南西側(cè)與東南亞塊體接觸，南東側(cè)為西太平洋構(gòu)造區(qū)[20]。現(xiàn)今華南地區(qū)由揚(yáng)子和華夏地塊經(jīng)過(guò)多期復(fù)合演變形成現(xiàn)今的基本形態(tài)[21]，其大地構(gòu)造與演化受歐亞板塊、太平洋板塊和菲律賓海板塊共同作用的影響，動(dòng)力學(xué)背景復(fù)雜，研究區(qū)內(nèi)發(fā)育多條活動(dòng)斷裂。華南地區(qū)歷史地震活動(dòng)強(qiáng)烈，1604年曾發(fā)生泉州海外8.0級(jí)地震。2010年以來(lái)該區(qū)域以中強(qiáng)地震為主，先后發(fā)生了2013年廣東東源5.1級(jí)地震、2013年福建仙游5.2級(jí)地震和2018年臺(tái)灣海峽6.2級(jí)地震等多次中強(qiáng)地震。圖1(a)顯示了2010年以來(lái)的地震主要集中在長(zhǎng)樂(lè)-詔安斷裂帶、邵武-河源斷裂帶以及濱海斷裂帶。

時(shí)變重力觀(guān)測(cè)網(wǎng)有助于獲取較高時(shí)空分辨率的重力場(chǎng)信息,并有效監(jiān)測(cè)地震重點(diǎn)危險(xiǎn)區(qū)地球物理場(chǎng)的動(dòng)態(tài)變化特征，以識(shí)別區(qū)域潛在強(qiáng)震風(fēng)險(xiǎn)源，此前已在青藏高原中強(qiáng)地震[7-9]的中長(zhǎng)期危險(xiǎn)區(qū)預(yù)測(cè)和地球科學(xué)研究中發(fā)揮了重要的作用。中國(guó)地震局自20世紀(jì)70至80年代開(kāi)始在華南地區(qū)開(kāi)展時(shí)變重力觀(guān)測(cè)。經(jīng)過(guò)多次升級(jí)和改造，至2019年華南地區(qū)已建成了測(cè)點(diǎn)分布較均勻、有絕對(duì)基準(zhǔn)控制的高質(zhì)量陸面時(shí)變重力觀(guān)測(cè)系統(tǒng)，并基本覆蓋福建和廣東陸地主要的構(gòu)造和斷裂帶，如圖1(b)所示。由圖1(b)可知，測(cè)網(wǎng)內(nèi)有廈門(mén)、武夷山、平潭、廣州和韶關(guān)絕對(duì)重力基準(zhǔn)點(diǎn)，平均兩年重復(fù)觀(guān)測(cè)一次，精度優(yōu)于5×10-8m/s2。相對(duì)重力重復(fù)測(cè)量點(diǎn)有550個(gè)，測(cè)段640段，測(cè)點(diǎn)間距在30～50 km范圍內(nèi)，平均6個(gè)月重復(fù)觀(guān)測(cè)一次，采用4臺(tái)CG-5型相對(duì)重力儀，兩兩一組進(jìn)行復(fù)測(cè)。

2 貝葉斯重力平差模型

陸地重力數(shù)據(jù)處理的核心是平差計(jì)算[22]。目前常用的經(jīng)典重力平差方法采用最小二乘方法獲得觀(guān)測(cè)點(diǎn)的最佳估值，并假定參與觀(guān)測(cè)的每臺(tái)重力儀漂移率是線(xiàn)性的[23-24]。經(jīng)典平差方程可表示為

(1)

(2)

式(1)和式(2)也可合并簡(jiǎn)化為

(3)

式中，Normal(·)表示正態(tài)分布，均值為0，方差為W-1；A、D、G分別為觀(guān)測(cè)順序矩陣、段差觀(guān)測(cè)時(shí)間矩陣和絕對(duì)點(diǎn)矩陣；x、v代表點(diǎn)值和漂移率，為待求參數(shù)；y為觀(guān)測(cè)段差。

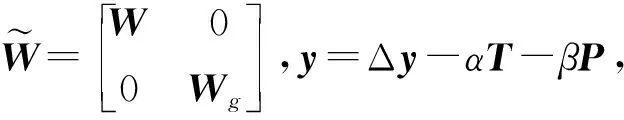
SX=Y

(4)

式(4)為絕對(duì)重力約束下的觀(guān)測(cè)方程，Δy為同一臺(tái)儀器在相鄰兩測(cè)點(diǎn)的重力讀數(shù)差，T為理論固體潮，α為潮汐因子；P為大氣壓力負(fù)荷引起的重力變化，β為氣壓導(dǎo)納。

通過(guò)求上述平差方程的最大似然估計(jì)，可以得到x、v的最優(yōu)估計(jì)。首先，可以由式(1)—式(3)，給出多臺(tái)相對(duì)重力儀和絕對(duì)重力觀(guān)測(cè)的聯(lián)合概率密度分布

(5)

區(qū)別于經(jīng)典平差對(duì)漂移的線(xiàn)性假設(shè)以及分段零漂的處理方式[25]，本文采用的貝葉斯重力平差方法[19]提供了非線(xiàn)性漂移的計(jì)算模型。該方法假定相對(duì)重力儀的漂移率隨時(shí)間變化光滑，將其作為先驗(yàn)條件，可表示為

(6)

(7)

式中，l為儀器待求格值系數(shù)。

基于貝葉斯公式，后驗(yàn)概率似然函數(shù)可表示為

(8)

(9)

式中，L(y|v)可由方程式(5)得到；π(v)為漂移率的先驗(yàn)分布，并采用ABIC方法[26]進(jìn)行貝葉斯估計(jì)模型的擬合優(yōu)良性分析。

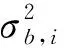
對(duì)于相對(duì)重力儀的格值優(yōu)化問(wèn)題，測(cè)網(wǎng)中如果同時(shí)存在兩個(gè)或多個(gè)獨(dú)立觀(guān)測(cè)的絕對(duì)重力點(diǎn)，通過(guò)上述貝葉斯優(yōu)化計(jì)算，即可以實(shí)現(xiàn)格值系數(shù)的優(yōu)化計(jì)算[27]。

不同區(qū)域的數(shù)據(jù)應(yīng)根據(jù)實(shí)際情況選擇不同平差方法進(jìn)行數(shù)據(jù)處理。對(duì)于小范圍的重力測(cè)量，按經(jīng)典平差的線(xiàn)性漂移模型解算即可。但對(duì)于雙程閉合時(shí)間長(zhǎng)，空間測(cè)點(diǎn)地理跨度大的華南區(qū)域流動(dòng)重力測(cè)量，則需重點(diǎn)考慮儀器的非線(xiàn)性漂移特性，以提高數(shù)據(jù)精度。因此本文重點(diǎn)對(duì)比經(jīng)典與貝葉斯平差方法在華南區(qū)域的差異和方法的適用性。

3 華南時(shí)變流動(dòng)重力觀(guān)測(cè)質(zhì)量評(píng)價(jià)

在陸地時(shí)變重力數(shù)據(jù)處理中，相對(duì)重力儀的非線(xiàn)性漂移特性和格值系數(shù)變化是兩個(gè)主要的誤差來(lái)源。本文分別采用經(jīng)典平差和貝葉斯重力平差方法處理了華南測(cè)網(wǎng)2015—2018年的重力觀(guān)測(cè)數(shù)據(jù)，基于段差殘差、段差互差和絕對(duì)點(diǎn)值差參數(shù)，量化相對(duì)重力儀非線(xiàn)性漂移特征和格值系數(shù)的不確定性，并基于絕對(duì)重力基準(zhǔn)觀(guān)測(cè)的交叉檢驗(yàn)評(píng)價(jià)華南時(shí)變重力數(shù)據(jù)質(zhì)量，分析區(qū)域的重力場(chǎng)時(shí)空特征。

3.1 儀器不確定性評(píng)價(jià)

3.1.1 漂移率變化

選取2018 C1期華南測(cè)網(wǎng)的觀(guān)測(cè)數(shù)據(jù)進(jìn)行分析，該測(cè)期絕對(duì)重力觀(guān)測(cè)有廈門(mén)、武夷山、平潭、廣州和韶關(guān)5個(gè)測(cè)點(diǎn)，標(biāo)準(zhǔn)差優(yōu)于5×10-8m/s2，與流動(dòng)重力觀(guān)測(cè)時(shí)間準(zhǔn)同步。分別采用CG5-1316、CG5-814(福建測(cè)網(wǎng))和CG5-232、CG5-369(廣東測(cè)網(wǎng))4臺(tái)相對(duì)重力儀進(jìn)行同步觀(guān)測(cè)，并對(duì)廣福、蕉嶺等公共測(cè)點(diǎn)進(jìn)行聯(lián)測(cè)。為便于討論，下文以FJ-1316、FJ-814、GD-232和GD-369命名4臺(tái)儀器，將3月和9月的測(cè)期分別命名為C1期和C2期。

圖2為4臺(tái)相對(duì)重力儀的線(xiàn)性和非線(xiàn)性漂移率變化。圖2可見(jiàn)4臺(tái)相對(duì)重力儀存在非線(xiàn)性漂移，且彼此間差異性明顯。儀器的漂移特性隨測(cè)量進(jìn)程呈不同的變化趨勢(shì)。FJ-1316的漂移率達(dá)0.8×10-5(m/s2)1 d(圖2(a))，觀(guān)測(cè)周期內(nèi)漂移率最小和最大值相差約0.15×10-5m/s2，其每日漂移率表現(xiàn)為逐漸增大后趨于穩(wěn)定的過(guò)程，而FJ-814的漂移率變化較穩(wěn)定。隨著儀器觀(guān)測(cè)時(shí)長(zhǎng)增加，GD-232在測(cè)量后半程的非線(xiàn)性漂移率明顯大于測(cè)量前期(圖2(b))。

圖1 華南地區(qū)地震地質(zhì)構(gòu)造背景與時(shí)變重力觀(guān)測(cè)網(wǎng)絡(luò)Fig.1 The geologic structure seismic activity and time-varying gravity observation network in South China

圖2 華南測(cè)網(wǎng)彈簧重力儀的漂移率變化Fig.2 Estimated drift rates of four gravimeters at Fujian and Guangdong survey campaign

圖3為采用經(jīng)典和貝葉斯重力平差方法計(jì)算的段差殘差變化。平差后的段差殘差基本分布在±30×10-8m/s2范圍。貝葉斯重力平差方法的殘差(圖3(b))基本呈隨機(jī)分布狀態(tài)，幅值略小于經(jīng)典平差結(jié)果(圖3(a))。4臺(tái)儀器的段差殘差統(tǒng)計(jì)直方圖(圖3(c))顯示出貝葉斯平差方法中小于±5×10-8m/s2的段差殘差數(shù)量多于經(jīng)典平差法。兩種方法的段差殘差分布都符合高斯分布特征，經(jīng)典平差的段差殘差標(biāo)準(zhǔn)差為6.8×10-8m/s2，貝葉斯平差的段差殘差標(biāo)準(zhǔn)差為6.17×10-8m/s2。從段差殘差結(jié)果和統(tǒng)計(jì)參數(shù)特征看，在華南測(cè)網(wǎng)貝葉斯重力平差結(jié)果略好于經(jīng)典方法。

3.1.2 格值系數(shù)變化檢測(cè)

相對(duì)重力儀格值是影響重力測(cè)量誤差的重要因素。目前地震重力觀(guān)測(cè)中相對(duì)重力儀的格值系數(shù)通常采用基線(xiàn)場(chǎng)標(biāo)定結(jié)果[28]，但基線(xiàn)場(chǎng)標(biāo)定間隔時(shí)間長(zhǎng)[27]，其周期長(zhǎng)達(dá)3～5 a，不能滿(mǎn)足重力觀(guān)測(cè)半年周期的需求。本文中所采用的4臺(tái)重力儀，F(xiàn)J-814和FJ-1316初始格值由儀器廠(chǎng)家給定。GD-232查無(wú)基線(xiàn)場(chǎng)標(biāo)定記錄，GD-369在2010年進(jìn)行過(guò)基線(xiàn)場(chǎng)標(biāo)定，標(biāo)定格值為1.000 456。由于福建測(cè)網(wǎng)由廠(chǎng)家給定的初始格值是在實(shí)驗(yàn)室觀(guān)測(cè)條件下獲得，廣東測(cè)網(wǎng)的基線(xiàn)場(chǎng)標(biāo)定周期過(guò)長(zhǎng)，因此每次開(kāi)展重力觀(guān)測(cè)前儀器都進(jìn)行了實(shí)地測(cè)區(qū)的格值標(biāo)定。但實(shí)際測(cè)區(qū)的格值標(biāo)定仍存在著由于段差過(guò)小、觀(guān)測(cè)人員操作差異等不確定性因素，為此本文應(yīng)用貝葉斯重力平差優(yōu)化模型，通過(guò)高精度的絕對(duì)重力基準(zhǔn)點(diǎn)，在平差方程中采用貝葉斯優(yōu)化方法進(jìn)行格值系數(shù)估計(jì)，依據(jù)ABIC準(zhǔn)則尋找最優(yōu)超參數(shù)，進(jìn)而得到絕對(duì)重力約束的格值系數(shù)。

FJ-1316和FJ-814在研究時(shí)段格值系數(shù)不變(圖4)，F(xiàn)J-1316和FJ-814的初始格值分別為1.000 655和0.999 934，GD-232的格值系數(shù)變化在2016 C2至2018 C1的格值系數(shù)為0.998 610，GD-369在2016 C2至2018 C1期間為0.999 902。由于研究時(shí)段內(nèi)僅有兩期絕對(duì)重力觀(guān)測(cè)(2015年12月和2018年1月)，因此2016 C1至2017 C2這4期選用2015年12月的絕對(duì)重力觀(guān)測(cè)為基準(zhǔn)，2018 C1以2018年1月的絕對(duì)重力觀(guān)測(cè)作為基準(zhǔn)。2016 C1和2018 C1兩期絕對(duì)和相對(duì)觀(guān)測(cè)時(shí)間準(zhǔn)同步。

基于各期的絕對(duì)重力點(diǎn)基準(zhǔn)，采用貝葉斯重力平差方法計(jì)算2015年—2018年4臺(tái)儀器優(yōu)化的格值系數(shù)。表1列出了各期的優(yōu)化格值系數(shù)和格值偏差(即初始格值與優(yōu)化格值之差)統(tǒng)計(jì)。圖4為華南測(cè)網(wǎng)相對(duì)重力儀初始和優(yōu)化格值系數(shù)隨時(shí)間的變化，圖中用紫色虛線(xiàn)標(biāo)示出絕對(duì)重力觀(guān)測(cè)的時(shí)間。華南測(cè)區(qū)貝葉斯格值優(yōu)化的格值系數(shù)與格值偏差統(tǒng)計(jì)見(jiàn)表1。如表1和圖4所示，研究時(shí)段內(nèi)福建測(cè)網(wǎng)的格值系數(shù)偏差明顯大于廣東測(cè)網(wǎng)。FJ-1316的優(yōu)化格值與初始格值的平均偏差約6.28×10-4，最大偏差約7.02×10-4。廣東測(cè)網(wǎng)內(nèi)GD-369和GD-232的優(yōu)化格值與初始格值的平均偏差為4.6～6.23×10-5，最大偏差為2017 C2期GD-369的2.26×10-4。從圖4亦可見(jiàn)，在2016 C1—2016 C2期和2018 C1期，當(dāng)絕對(duì)重力和相對(duì)重力觀(guān)測(cè)時(shí)間近于同步時(shí)，GD-232和GD-369的優(yōu)化格值系數(shù)和初始格值系數(shù)更為接近，一致性較好(二者的差值小)。

表1 華南測(cè)區(qū)貝葉斯格值優(yōu)化的格值系數(shù)與格值偏差統(tǒng)計(jì)

福建測(cè)網(wǎng)格值偏差較大的主要原因主要在于儀器性能及標(biāo)定周期過(guò)長(zhǎng)。從圖5段差互差的相關(guān)性統(tǒng)計(jì)可見(jiàn)，福建重力測(cè)網(wǎng)內(nèi)主要段差分布在±80×10-5m/s2范圍，而儀器格值系數(shù)出現(xiàn)5.89×10-4的偏差，將可能引起47×10-8m/s2的誤差，相比儀器非線(xiàn)性漂移變化，格值系數(shù)的誤差可能?chē)?yán)重影響整網(wǎng)平差結(jié)果的準(zhǔn)確性和可靠性。

雖然FJ-1316和FJ-814儀器的優(yōu)化格值與初始格值偏差較大，但二者格值偏差量級(jí)接近(表1)。以2018 C1期為例，格值優(yōu)化前后福建與廣東段差的互差范圍都分布在±0.025×10-5m/s2范圍，仍符合地震重力測(cè)量規(guī)范的要求。從優(yōu)化前后段差互差相關(guān)性(圖5)看，格值優(yōu)化后段差互差的變化不明顯。因此，當(dāng)兩臺(tái)儀器格值同步發(fā)生變化，僅依據(jù)儀器之間的互差不足以評(píng)價(jià)結(jié)果可靠性，需要進(jìn)一步通過(guò)測(cè)網(wǎng)內(nèi)的絕對(duì)重力測(cè)量結(jié)果開(kāi)展交叉驗(yàn)證。

圖3 段差殘差圖Fig.3 Gravity difference residuals

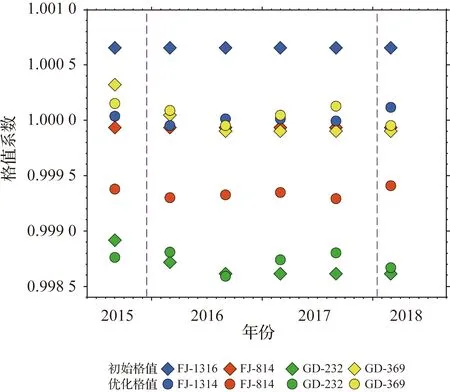
圖4 華南測(cè)網(wǎng)相對(duì)重力儀初始和優(yōu)化格值系數(shù)的變化(圖中虛線(xiàn)為絕對(duì)重力觀(guān)測(cè)時(shí)間)Fig.4 Changes of calibration scale factor of relative gravimeters in Huanan network

圖5 分別采用初始和優(yōu)化格值系數(shù)時(shí)測(cè)點(diǎn)段差與儀器互差變化Fig.5 Gravity difference of two adjacent stations and gravity difference of the simultaneous observation instruments in the case of optimized and calibrated scale factor

在既有絕對(duì)觀(guān)測(cè)也有相對(duì)觀(guān)測(cè)的混合重力測(cè)網(wǎng)中，高精度、獨(dú)立的絕對(duì)重力觀(guān)測(cè)可用來(lái)驗(yàn)證相對(duì)重力的觀(guān)測(cè)結(jié)果，因此進(jìn)一步采用絕對(duì)重力交叉驗(yàn)證的方法對(duì)格值優(yōu)化結(jié)果進(jìn)行評(píng)估。交叉驗(yàn)證(cross-validation)基本思想是將原始數(shù)據(jù)進(jìn)行分組，一部分作為訓(xùn)練集來(lái)訓(xùn)練模型，另一部分作為驗(yàn)證集測(cè)試評(píng)價(jià)訓(xùn)練模型。首先將絕對(duì)重力點(diǎn)分組，選擇通過(guò)測(cè)網(wǎng)中部分絕對(duì)點(diǎn)作為平差起算點(diǎn)參與平差，解算得到相對(duì)重力推算的絕對(duì)重力點(diǎn)值，并與絕對(duì)重力實(shí)測(cè)的絕對(duì)點(diǎn)值相減得到絕對(duì)點(diǎn)值差。因此，絕對(duì)點(diǎn)值差可以作為相對(duì)觀(guān)測(cè)與絕對(duì)觀(guān)測(cè)一致性的檢驗(yàn)指標(biāo)，反映重力儀格值的準(zhǔn)確程度。

平潭和韶關(guān)作為起算點(diǎn)，廈門(mén)、武夷山和廣州作為檢驗(yàn)點(diǎn)(對(duì)應(yīng)圖6(b))的絕對(duì)點(diǎn)值差見(jiàn)表2。由表2可知，優(yōu)化格值的絕對(duì)點(diǎn)值差相比初始格值的絕對(duì)點(diǎn)值差更小。其中，廈門(mén)和武夷山變化較為顯著，優(yōu)化格值的絕對(duì)點(diǎn)值差減小20～60×10-8m/s2，即采用優(yōu)化格值推算的重力值更符合用于檢驗(yàn)的絕對(duì)重力實(shí)際測(cè)量值。因此，與儀器間段差互差的相關(guān)性方法相比，采用絕對(duì)重力交叉驗(yàn)證格值準(zhǔn)確性的方法更有效。

表2 華南測(cè)區(qū)貝葉斯格值優(yōu)化前后的絕對(duì)重力抽樣檢驗(yàn)

3.2 絕對(duì)重力交叉驗(yàn)證

在上文基礎(chǔ)上，對(duì)測(cè)網(wǎng)內(nèi)5個(gè)絕對(duì)點(diǎn)依次進(jìn)行交叉驗(yàn)證，以全面檢驗(yàn)貝葉斯重力平差方法的有效性和可靠性。以2018 C1測(cè)期準(zhǔn)同步的絕對(duì)重力觀(guān)測(cè)，設(shè)計(jì)4組方案(表3)對(duì)相對(duì)重力平差結(jié)果進(jìn)行交叉驗(yàn)證。

表3 絕對(duì)重力交叉驗(yàn)證

圖6是分別基于表3方案采用經(jīng)典和貝葉斯重力平差方法得到的4組絕對(duì)點(diǎn)值差。由圖6可知，貝葉斯重力平差方法(采用優(yōu)化格值)的結(jié)果明顯優(yōu)于經(jīng)典平差(采用初始格值的)的結(jié)果，這與儀器格值誤差得到有效抑制有關(guān)。而隨著用于平差的絕對(duì)點(diǎn)增加，兩種方法的點(diǎn)值差較差逐步變小。在圖6(a)中，采用平潭1個(gè)點(diǎn)估算時(shí)，兩種平差方法計(jì)算的點(diǎn)值差較差為20～60×10-8m/s2。而當(dāng)采用平潭、韶關(guān)兩個(gè)點(diǎn)估算時(shí)(圖6(b))，位于測(cè)網(wǎng)中部的廣州和廈門(mén)貝葉斯重力平差相比于經(jīng)典平差的點(diǎn)值差都減小約20×10-8m/s2，測(cè)網(wǎng)邊緣的武夷山改善更顯著，其貝葉斯重力平差相比于經(jīng)典平差的點(diǎn)值差減小57×10-8m/s2。從圖6(a)與6(b)經(jīng)典平差的武夷山點(diǎn)值差的變化亦可見(jiàn)，受FJ-814和FJ-1316兩臺(tái)CG-5彈簧重力儀的格值系數(shù)不準(zhǔn)確的影響，相對(duì)重力平差的結(jié)果與絕對(duì)重力觀(guān)測(cè)差異較大。在圖6(c)和6(d)中，兩種方法的平潭絕對(duì)點(diǎn)值差較差約10×10-8m/s2。綜合以上，測(cè)網(wǎng)內(nèi)絕對(duì)重力的交叉驗(yàn)證結(jié)果表明貝葉斯重力平差方法得到的優(yōu)化格值系數(shù)比初始格值系數(shù)更準(zhǔn)確。

為進(jìn)一步研究不同平差方法和絕對(duì)點(diǎn)約束下的點(diǎn)值結(jié)果空間差異性，采用表3中方案b—方案d分別對(duì)華南測(cè)網(wǎng)中不同絕對(duì)點(diǎn)起算下貝葉斯重力平差相比于經(jīng)典平差的點(diǎn)值差空間分布進(jìn)行了可視化，如圖7所示，可知福建測(cè)網(wǎng)的因平差方法產(chǎn)生的影響明顯大于廣東測(cè)網(wǎng)，筆者認(rèn)為這主要與測(cè)量?jī)x器的格值誤差有關(guān)(表1)。值得注意的是，隨著用于平差的絕對(duì)點(diǎn)增加，平差方法引起的結(jié)果差異逐漸減小，且在測(cè)網(wǎng)邊緣處的點(diǎn)值精度改善最明顯。因此，重力觀(guān)測(cè)網(wǎng)內(nèi)絕對(duì)點(diǎn)的布置應(yīng)盡量均勻，且為保證點(diǎn)值精度，至少有兩個(gè)以上的絕對(duì)點(diǎn)進(jìn)行平差。當(dāng)選擇平潭和韶關(guān)兩個(gè)絕對(duì)點(diǎn)為起算點(diǎn)(圖7(a))時(shí)，測(cè)網(wǎng)邊緣的武夷山點(diǎn)值差都明顯大于其他點(diǎn)。219個(gè)測(cè)點(diǎn)的點(diǎn)值差為10～20×10-8m/s2，75%測(cè)點(diǎn)點(diǎn)值差分布在±30×10-8m/s2范圍，均值為20×10-8m/s2。當(dāng)測(cè)網(wǎng)內(nèi)有韶關(guān)、武夷山、廈門(mén)和廣州4個(gè)絕對(duì)點(diǎn)作為起算(圖7(c))時(shí)，284個(gè)測(cè)點(diǎn)的點(diǎn)值差在±10×10-8m/s2。而且點(diǎn)值差的分布更接近正態(tài)分布，均值為18.8×10-8m/s2。由圖6—圖7可知，華南測(cè)網(wǎng)觀(guān)測(cè)資料由于相對(duì)重力儀非線(xiàn)性漂移和格值系數(shù)不準(zhǔn)確共可引起約20×10-8m/s2的不確定性，且通過(guò)貝葉斯方法可以有效抑制。

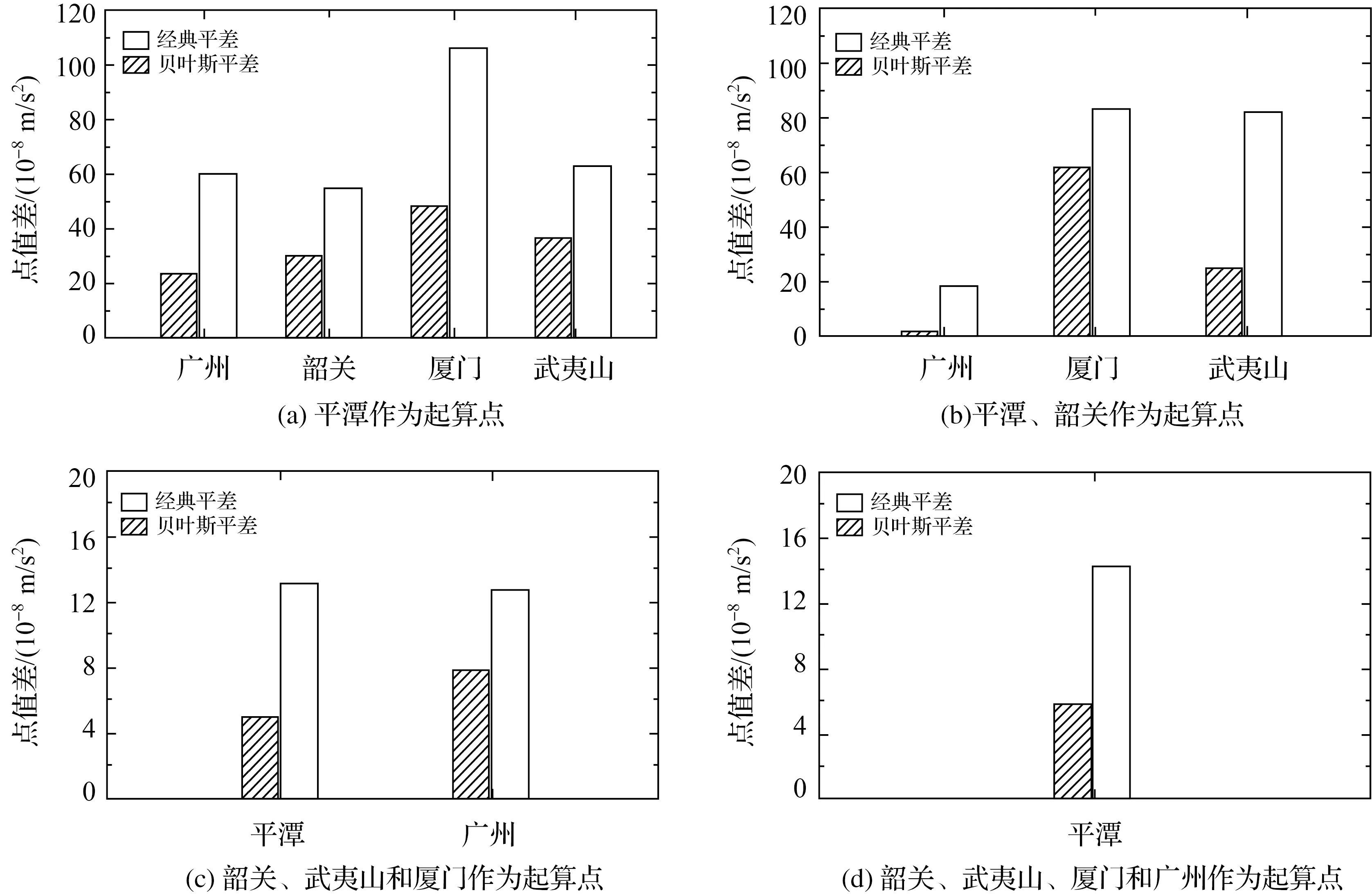
圖6 不同起算點(diǎn)下經(jīng)典和貝葉斯平差的絕對(duì)點(diǎn)點(diǎn)值估算誤差Fig.6 Differences between estimated gravity values at each absolute gravity station by classical adjustment and bayesian adjustment approach when different absolute gravity stations are using in the base observations

圖7 不同絕對(duì)點(diǎn)起算下貝葉斯重力平差相比于經(jīng)典平差的點(diǎn)值差空間分布Fig.7 Differences between estimated gravity values by classical adjustment and Bayesian adjustment approach when different absolute gravity stations are using in the base observations

4 結(jié) 論

陸地時(shí)變微重力觀(guān)測(cè)是研究地殼內(nèi)部物質(zhì)變化的重要手段。華南重力網(wǎng)具有測(cè)點(diǎn)間距大、覆蓋范圍廣、觀(guān)測(cè)時(shí)間長(zhǎng)和對(duì)重力資料解算精度要求高等特點(diǎn)。本文采用華南地區(qū)2015年—2018年的實(shí)測(cè)流動(dòng)重力觀(guān)測(cè)資料，引入貝葉斯平差方法，量化分析了由于相對(duì)重力儀的非線(xiàn)性漂移、一次項(xiàng)系數(shù)不準(zhǔn)確的影響，得到以下結(jié)論。

(1) 華南重力測(cè)網(wǎng)使用的4臺(tái)相對(duì)重力儀存在非線(xiàn)性漂移，且彼此間差異性明顯，其中福建測(cè)區(qū)使用的FJ-1316儀器漂移率最高達(dá)0.8×10-8m/s2/d。從段差殘差結(jié)果和統(tǒng)計(jì)參數(shù)特征看，貝葉斯平差結(jié)果略好于經(jīng)典方法。

(2) 對(duì)儀器格值系數(shù)誤差的評(píng)估結(jié)果發(fā)現(xiàn)，福建測(cè)網(wǎng)FJ-1316和FJ-814的初始與優(yōu)化格值偏差平均值為5.89～6.28×10-4，廣東測(cè)網(wǎng)GD-232和GD-369初始與優(yōu)化的格值系數(shù)偏差平均值為4.2～6.23×10-5。應(yīng)用絕對(duì)重力交叉檢驗(yàn)法對(duì)格值優(yōu)化結(jié)果進(jìn)行評(píng)價(jià)，優(yōu)化后的檢驗(yàn)絕對(duì)重力點(diǎn)值差可減小約20～60×10-8m/s2重力變化，采用貝葉斯方法優(yōu)化后格值的平差結(jié)果更符合用于檢驗(yàn)的絕對(duì)重力測(cè)量值。值得注意的是，用于福建測(cè)網(wǎng)中的兩臺(tái)相對(duì)重力儀，由于兩臺(tái)儀器格值系數(shù)同步變化且相互間差異較小，導(dǎo)致僅從儀器間互差來(lái)驗(yàn)證結(jié)果可靠性很難發(fā)現(xiàn)存在的格值系數(shù)誤差。

(3) 通過(guò)測(cè)網(wǎng)中的絕對(duì)重力基準(zhǔn)開(kāi)展交叉檢驗(yàn)，隨著用于平差的絕對(duì)點(diǎn)增加，經(jīng)典和貝葉斯平差方法的差異逐漸減小，且在測(cè)網(wǎng)邊緣處的點(diǎn)值精度改善最明顯，分析認(rèn)為這主要是由于儀器格值誤差得到有效抑制。華南測(cè)網(wǎng)觀(guān)測(cè)資料由于相對(duì)重力儀非線(xiàn)性漂移和格值系數(shù)不準(zhǔn)確共可引起約20×10-8m/s2的不確定性，且通過(guò)貝葉斯方法可以有效抑制。

本文基于最新的貝葉斯平差方法，著重從相對(duì)重力儀的不確定參數(shù)優(yōu)化(漂移非線(xiàn)性特征、格值系數(shù))和絕對(duì)重力交叉檢驗(yàn)技術(shù)對(duì)華南地區(qū)的時(shí)變重力數(shù)據(jù)進(jìn)行了分析。本文研究方法和思路同樣適合于中國(guó)大陸其他地區(qū)的重力數(shù)據(jù)質(zhì)量評(píng)價(jià)，也有助于更合理和客觀(guān)地開(kāi)展重力場(chǎng)變化與斷層運(yùn)動(dòng)、地殼形變、強(qiáng)震孕育和物質(zhì)變遷等方面的研究。