基于損傷塑性模型的超高性能混凝土數值模擬
和鎵遠
(同濟大學, 上海 200092 )
1 研究背景及意義
超高性能混凝土(UHPC,Ultra-High Performance Concrete),又稱活性粉末混凝土(RPC,Reactive Powder Concrete),因其極高的密實度而性能優異。為了高效精確地研究UHPC 力學性能,國內外已針對其數值模擬方法開展了相關研究。Bahij 等[1]研究了UHPC 梁抗剪性能的數值模擬方法,精度較高。管品武等[2]對不同UHPC 本構模型進行總結,并驗證了高強鋼筋UHPC 梁有限元模型的合理性。張燎軍等[3]建立UHPC 簡支梁的損傷塑性模型,并嘗試將模擬方法應用于重力壩設計中。
目前ABAQUS 的混凝土損傷塑性模型(CDP,Concrete Damaged Plasticity)較多用于普通混凝土結構分析,模擬UHPC 材料較少。本文依據Yu Jiangjiang[4]等的試驗數據,基于ABAQUS 建立UHPC 立方體受壓損傷塑性模型,并與文獻中的試驗結果對比,驗證分析方法的合理性,為UHPC 的非線性有限元分析提供參考。
2 混凝土損傷塑性模型
文獻[4]針對“FA-2”和“CA-1.5”兩種配比UHPC,進行了立方體抗壓、狗骨試件單軸抗拉等試驗,本文現使用ABAQUS 建立CDP 模型,對UHPC立方體試件進行數值模擬。
2.1 UHPC 單軸受壓本構模型
UHPC 單軸受壓應力-應變曲線采用吳有明[5]定義的本構模型,見式(1)。

曲線上升段參數A 以及其他相關參數參考郭曉宇等[6]歸納的擬合公式確定:首先將試驗實測的UHPC 立方體抗壓強度 fcu,由式(2)換算得到棱柱體抗壓強度 fc,再由式(3)~式(5)計算得到混凝土峰值壓應變εco、彈性模量E 和參數A。曲線下降段參數經試算取α =4,UHPC 模型相關參數見表 1。此外,模型中UHPC 密度取值2.5×103kg/m3,泊松比取值0.2。

2.2 UHPC 單軸受拉本構模型
模型中UHPC 單軸受拉應力-應變曲線上升段近似為線性直線,考慮文獻[4]中試件拉伸時無應變硬化現象,所以下降段采用江見鯨[7]提出的指數曲線模型,見式(6)。

式中, ft為混凝土極限抗拉強度,εcr為混凝土拉應力峰值時的應變,αt為控制下降段的軟化系數,αt值越大,混凝土脆性越大,本文模型經試算取值αt=1000。
2.3 損傷變量
CDP 模型引入損傷因子來考慮材料不可逆的損傷退化,本文依據以上本構關系,基于能量損失原理,采用面積法計算損傷變量d ,公式為:
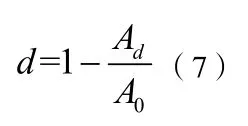
其中,Ad為損傷材料的應變能,即應力-應變曲線下的面積,A0為無損材料的應變能,即斜率為 E0直線下的三角形面積,
2.4 其他塑性參數
ABAQUS 中還需要設置以下參數:雙軸極限抗壓強度與單軸極限抗壓強度比拉壓子午面上第二應力不變量之比Kc、膨脹角φ、勢函數偏心率∈以及粘性系數μ ,本文參考彭小婕等[8]的研究進行設置,見表 2。
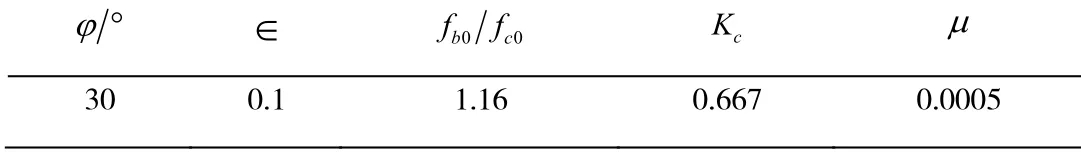
表2 模型其他塑性參數
3 模型分析
在ABAQUS 中采用C3D8R 實體單元,建立100mm×100mm×100mm 立方體受壓模型,網格劃分尺寸取5mm。表 3 為UHPC 立方體抗壓強度的模擬值與實測試驗結果,相差不超過5%,吻合較好,圖1 為模型的應力-應變曲線,數值模擬結果合理,所采用的本構關系能較好用于UHPC試件的損傷塑性分析。
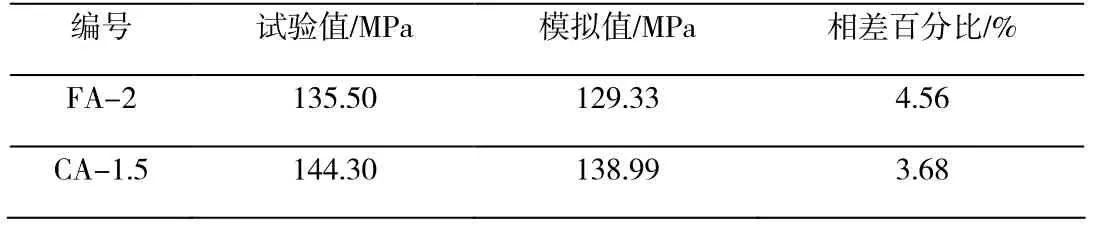
表3 數值模擬結果與試驗對比
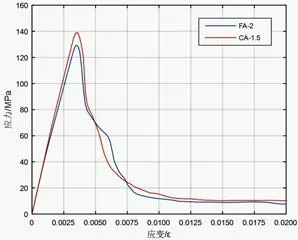
圖1 模型應力-應變曲線
圖2 為位移加載至2mm 時模型的塑性應變量(PEMAG)云圖,可見FA-2與CA-1.5 的破壞模式相近,塑性應變分布大致呈“X”型,集中在側面對角線、中部區域,而試驗中形成的沙漏形破壞體與模擬情況基本相符。

圖2 塑性應變云圖
4 結論
本文通過選取適當的UHPC 單軸受壓、單軸受拉本構關系,基于ABAQUS對文獻[4]中UHPC 立方體試件建立CDP 模型,并進行單調加載的非線性有限元分析,得出以下結論:
(1)通過采用文獻[6]總結歸納的擬合公式,可由UHPC 立方體抗壓強度這一項參數估算材料峰值應變、彈性模量等其他參數并應用于數值模擬中,結果較為精確。
(2)UHPC 立方體受壓CDP 模型的材料退化區域大致呈“X”型,立方體的各棱邊中部塑性應變較小,每面的對角線、中部區域損傷明顯,與立方體抗壓試驗的沙漏形破壞體較為相像。
(3)UHPC 損傷塑性模型結果與試驗結果吻合較好,說明文獻[5]的單軸受壓本構模型可用于UHPC 數值模擬,文獻[7]的指數式受拉本構模型能適用于無拉伸應變硬化現象的UHPC 有限元分析,也驗證了本文模型建立方法的合理性。

