基于ABAQUS的土工格柵層位置影響路面彎沉有限元分析

趙 昊， 賈孟宗

(西南交通大學，四川成都 610031)

加筋土的應用歷史已悠久[1]。土工格柵憑借著自身占地少、協調性好、適應性強等特點，在路基中被廣泛使用[2]。普通高速公路路基路面四分之一模型及土工格柵如圖1所示，其中，土工格柵可放置于公路各面層之間。徐超[3]通過平板荷載試驗方法研究了不同加筋材料和加筋層數對土工格柵加筋土地基承載特性的影響。隨著有限元軟件的發展，一些學者也通過數值模擬的方法對加筋土承載能力和變形特征進行了一定研究[4-5]。

在數值模擬時，不同的路基面層連接方式對路面彎沉值的影響甚至大于土工格柵本身的影響，本文基于ABAQUS對比分析了不同土工格柵位置、不同面層間相互作用對于路面彎沉最大值的影響。

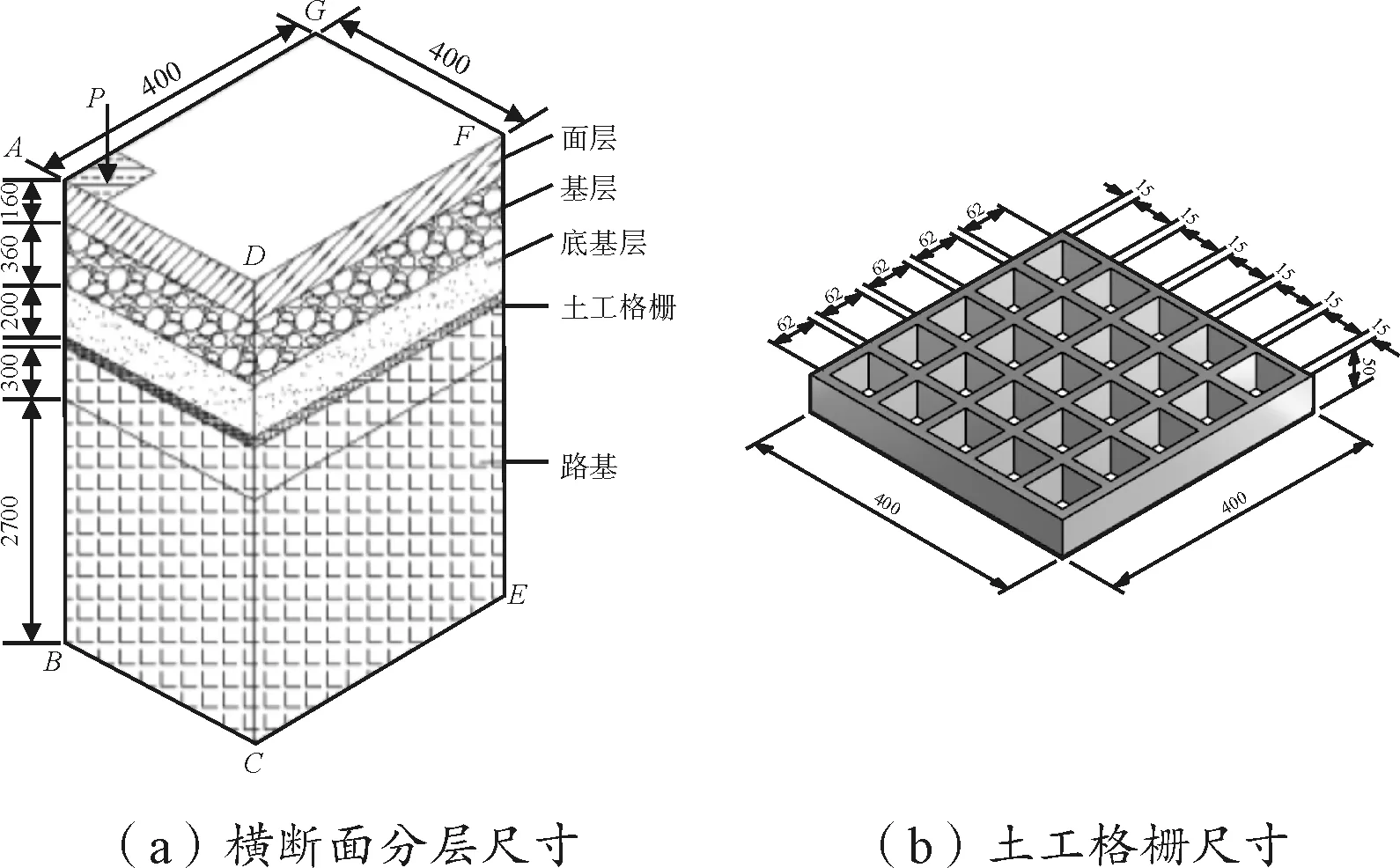
圖1 模型尺寸示意

1 材料模型驗證

高速公路各面層密度均為2×10-9t/mm3；路面厚度與材料參數如表1所示。

路基材料考慮拉壓非對稱Drucker-Prager模型：摩擦角β和膨脹角ψ均為40°，應力比K取1；率相關參數為冪法則乘數D=10，指數n=1；壓力P=0.7～1.5 MPa(本文取1.5 MPa)；Drucker-Prager模型的硬化參數如表2所示。

為驗證模型材料參數的正確性，采用1 m×1 m×1 m的正方體模型，輸入材料參數，測試Drucker-Prager模型本構關系曲線，測試后選取唯一節點，繪制其應力應變曲線，結果如圖2所示，其中TestCompression表示單元受壓時的應力應變曲線，TestPulling表示單元受拉時的應力應變曲線。結果表明：材料在拉伸、壓縮條件下表現出不同的應力應變關系，這與實際中土的材料本構關系相符。

表1 路面的幾何與材料參數

表2 Drucker-Prager模型的硬化參數

圖2 測試單元拉壓非對稱行為曲線

2 數值模擬

2.1 有限元模型

本文需要分析土工格柵位置對高速公路彎沉量的影響，共考慮了三種格柵位置，裝配完成后模型如圖3(a)、3(b)、3(c)所示。材料參數選取如表1、表2所示，模型網格數量結點總數: 67 183單元總數: 57 387，部件間的連接方式非別為綁定連接、面面接觸。

圖3 有限元模型

2.2 荷載及邊界

載荷條件：重力Z軸分量為-9 810 N/tonne；頂端角點50 mm×100 mm區域施加壓強載荷(p=1.5 MPa)。結果如圖4所示。

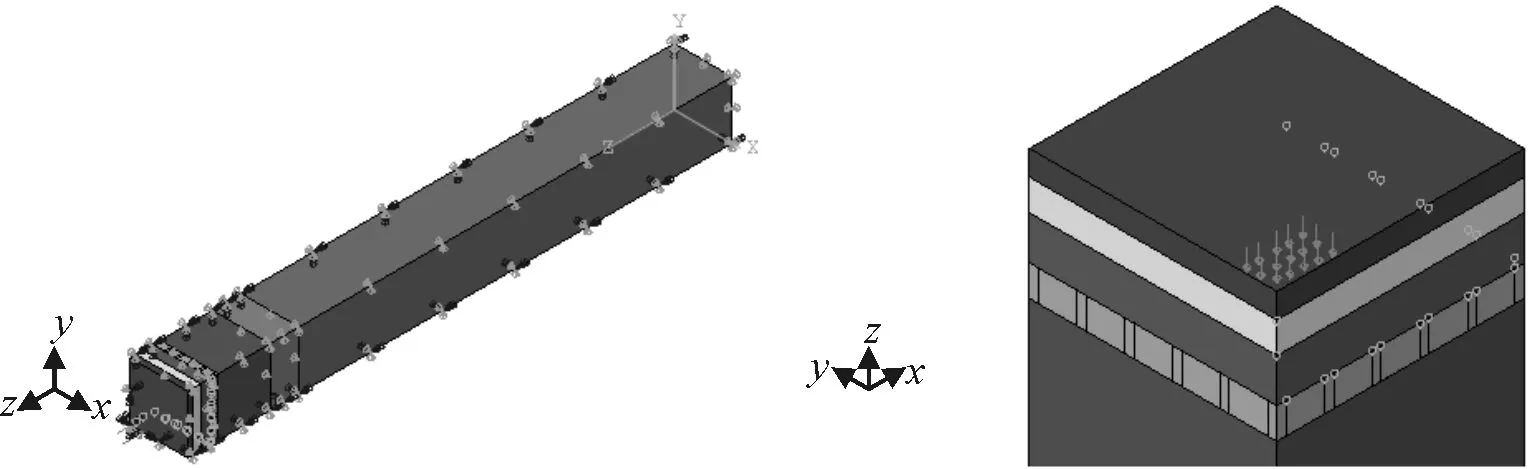
圖4 荷載及邊界

邊界條件：由于本文中模型取為1/4對稱模型，因此在全局坐標系中，模型x=0平面面施加x平面對稱邊界X=Ry=Rz=0；y=0面施加y平面對稱邊界Y=Rx=Rz=0；x=400 mm平面約束其法向X=0；y=400 mm平面約束其法向Y=0；底部z=0處約束其法向位移Z=0位移的四周和底端施加法相約束。

2.3 數值模擬結果

高速公路層與層之間考慮兩種連接形式：表面與表面綁定(a)；面面接觸(b)。

格柵層位于上部時，公路橫斷面內彎沉量及局部放大示意如圖5所示；格柵層位于中部時，公路橫斷面內彎沉量及局部放大示意如圖6所示；格柵層位于下部時，公路橫斷面彎沉量及局部放大示意如圖7所示。

(a)綁定鏈接

(a)綁定鏈接

(a)綁定鏈接

圖8 彎沉路徑

利用ABAQUS/Standard求解，在后處理模塊沿彎沉方向創建路徑1，如圖8所示；并繪制不同情況下高速公路的彎沉曲線如圖9所示，其中各圖名的含義如表3所示。

3 結論

(1) 根據路基路面工程施工過程，公路橫斷面上的每一層都按照一定的施工技術進行分層填埋、壓實。不同面層之間有著顯著的分界面，分界面之間既可以傳遞豎向力，又可以傳遞切向力。在有限元仿真計算中，需要通過考慮界面之間的相互作用來與實際情況對應。面層之間采用綁定連接與接觸連接時，這種不同的界面連接方式對路面彎沉量造成的影響甚至大于土工格柵布置位置的影響(約為5倍)，如圖9所示。因此，采用正確的有限元模型、界面連接方式對有限元分析結果極其重要。

(2) 無論界面間采用何種連接方式，有限元計算結果總是呈現這樣一個趨勢：隨著土工格柵層的上移，路面的彎沉量逐漸增大，而且對應位置的土工格柵層受力越發不均勻，這對于土工格柵長期工作將產生不良影響。

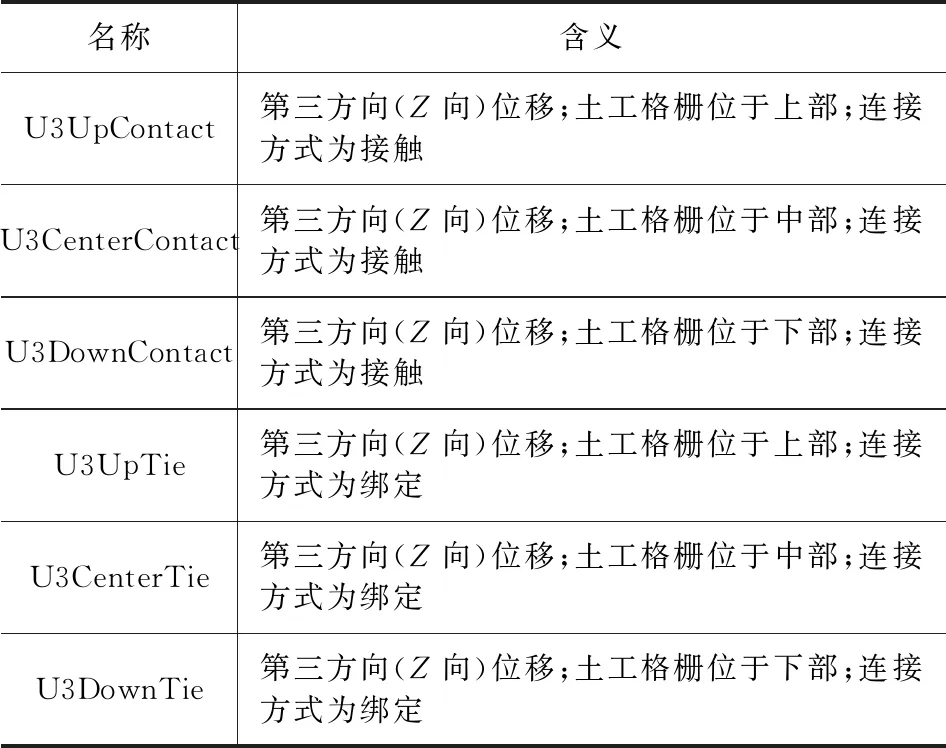
表3 曲線名稱及含義

圖9 彎沉曲線